考虑交叉口无效偏移率的干道协调数解算法

（兰州交通大学交通运输学院，甘肃兰州 730070）

在城市路网中，主干道承载着主要的交通负荷，因此，保证主干道上车流运行畅通与高效是缓解交通拥挤的关键所在。干线协调通过调节主干道连续交叉口的相位差，使车辆获得更多的通行权，尽可能避免停车现象的出现[1-4]。为获得干线最佳控制效果，干线协调主要通过最大绿波带法与最小延误法进行控制。最大绿波带常用的算法有图解法与数解法；最小延误法常用的算法有结合法与遗传算法等[5-9]。传统的干线绿波控制数解法，作为干线协调控制设计中最为常用的一种数值计算方法，具有简洁、实现方便、可操作性强的优点，特别是对车队行驶离散性较小、转弯车辆较少的双向对称式干道，能最大限度地保证车队通过干线多个交叉口的连续性，并在一些干线协调控制中得到广泛应用[10-12]。

近年来，一些文献结合实际情况对传统数解法进行了修正。粟红强等[13]设计了存在双周期交叉口和协调相位流量不均衡条件下的绿波带求解算法；陈旭梅等[14-15]提出了安宁绿波的理念；叶晓飞等提出考虑了行车延误的数解算法；就其对传统数解法绿波带带宽计算的修正，卢凯等[16]用“偏移绿信比”与“偏移绿灯时间”的概念取代“损失绿信比”与“损失绿灯时间”对传统数解法的绿波带带宽计算作出修正；王殿海等[17]通过考虑交叉口偏移对理想绿波带边缘的损失，提出新的绿波带带宽计算方法；但在实际绿波带的上边缘高于理想绿波带的上边缘，或实际绿波带的下边缘低于理想绿波带的下边缘的情况下，对绿波带宽计算便会忽略实际绿波带高（低）于理想绿波带上（下）边缘的部分，造成计算误差。本文在以往研究基础上，首先提出了交叉口无效偏移率与交叉口有效偏移量的概念，并根据交叉口的最大无效偏移率与交叉口相对于理想信号的实际偏移量，计算出实际交叉口相对理想绿波带上（下）边缘线的有效偏移量，从而对干线绿波带宽进行精确计算，然后提出了基于交叉口无效偏移率的数解算法来实现对称控制下干线绿波带宽最大化的最优控制，最后通过算例计算并与传统数解法进行对比，说明改进后算法在实现双向绿波协调对称控制中更为有效。

1 传统数解算法

数解法是通过寻找干线系统中各实际信号距离理想信号的最大挪移量的最小来获得干线交叉口最优相位差控制方案，实现干线绿波通过带宽度最大，其算法首先通过选用的干线最初公共周期来确定理想信号距离的迭代范围，对理想信号距离进行迭代，通过比较各理想信号间距下，实际交叉口相对理想信号的相邻挪移量之差最大值b，依据b最大原则确定最佳理想信号间距，最后根据最佳理想信号间距确定最佳公共周期，并根据各交叉口相对理想交叉口的位置所处方位确定相位差大小。

2 考虑交叉口无效偏移率的改进算法

2.1 交叉口无效偏移率

传统数解法在寻求实际交叉口距离理想信号最大挪移量最小的过程中，忽略了干线各交叉口绿信比的差别，使其在各交叉口绿信比偏差过大的干线系统中，产生最大挪移量的实际交叉口可能为绿信比最小的交叉口，从而对绿波带宽影响较大。由于干线各信号控制交叉口绿信比的不同，当各交叉口处于理想位置点时，则最大绿波带宽与各交叉口绿信比最小的那一个交叉口的绿信比相等[18]。绿信比较大的交叉口相对绿波带产生绿时富余量，在实际信号控制交叉口偏离理想信号点时不影响理想绿波带宽，不产生无效挪移。基于此，定义交叉口无效偏移率为实际交叉口偏移理想信号，且无理想绿波带宽产生改变的挪移量与理想信号距离的比值。

偏移理想间距的实际交叉口如图1所示。

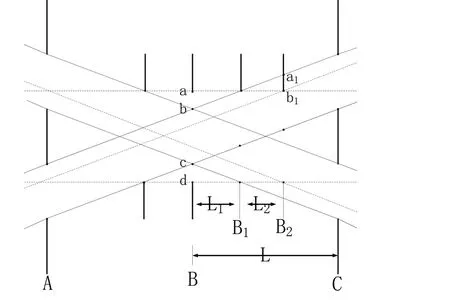
图1 偏移理想间距的实际交叉口

A、B、C三个交叉口位于理想信号位置，B1、B2为实际交叉口，理想信号距离为L，理想绿波带宽为交叉口A（瓶颈交叉口）的绿信比，由于B交叉口绿信比大于A交叉口，故B交叉口产生绿时富余量ab、cd，当交叉口B向右挪移L1至B1，绿时富余量ab被刚好消除，理想绿波带宽不变，同理向左挪移L1时绿时富余量cd被刚好消除。当交叉口B再向右挪移L2至B2，理想绿波带产生绿时损失a1b1，带宽变窄，则L1为交叉口B的最大无效偏移量，则交叉口最大无效偏移率为，它的值等于B交叉口与A交叉口绿信比之差。

2.2 交叉口有效偏移量及绿波带宽计算

当实际交叉口相对理想信号位置产生挪移，意味着实际交叉口相对理想绿波带上下边缘线产生有效偏移，在此定义交叉口相对理想绿波带上下边缘线的有效偏移量为：在上（下）行绿波带中，当交叉口偏移理想信号向右（左），则交叉口相对理想绿波带上边缘线的有效偏移量为交叉口的实际偏移量与最大无效偏移量之差；交叉口相对于理想滤波带下边缘线的有效偏移量为交叉口的实际偏移量与最大无效偏移量之和的相反数。当交叉口偏移理想信号向左（右），交叉口有效偏移量的计算恰好相反。

上行理想绿波带上下边缘线分别为l up与ldown，交叉口D与E为理想信号位置，1与2为实际交叉口，l为交叉口1的最大无效偏移量，x为交叉口1的实际偏移量，L为理想信号距离，则实际交叉口1相对于理想绿波带上边缘线的有效偏移量为：eup1=x-l；实际交叉口1相对于理想绿波带下边缘线的有效偏移量为：edown1=-x-l，位于理想信号异侧的实际交叉口有效偏移量计算恰好相反，则可得eup2与e down2。

由于交叉口的理想距离L=（v为通过绿波带速），根据相似三角形法则，得实际交叉口相对理想绿波带上边缘的绿波带宽减少量为；实际交叉口相对理想绿波带下边缘的绿波带宽减少量为。分别找出各实际交叉口相对理想绿波带上下边缘绿波带减少量的最大值eupmax与edownmax，实际绿波带宽为β=ω-eupmax-edownmax（ω为理想绿波带宽，eupmax=，edownmax=），而以往对绿波带宽计算忽略了δ部分，产生计算误差。

交叉口偏移对理想绿波带的修正如图2所示。

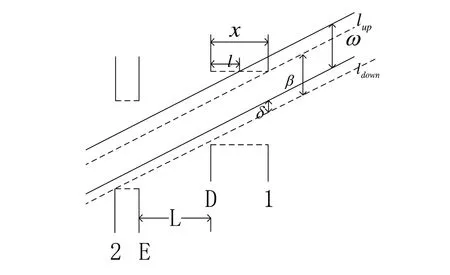
图2 交叉口偏移对理想绿波带的修正

2.3 考虑无效偏移率的数解算法

由于交叉口的无效偏移，并未对理想绿波带宽产生影响，因此在确定理想信号距离下考虑各交叉口最大无效偏移量，通过比较各交叉相对理想绿波带上边缘线最大有效偏移量与相对理想绿波带下边缘线最大有效偏移量之和e，依据e最小确定出该理想信号距离下最优相位差控制方案。算法首先通过交叉口最大无效偏移率计算各交叉口在理想信号距离下的有效偏移量，分别找出相对于理想绿波带上下边缘有效偏移量最大的交叉口，即对理想绿波带宽修正最大的交叉口，最大有效偏移量为正，则实际绿波带上边缘相对于理想绿波带上边缘下移，实际绿波带下边缘相对于理想绿波带下边缘上移。最大有效偏移量为负，则实际绿波带上边缘相对于理想绿波带上边缘上移，实际绿波带下边缘相对于理想绿波带下边缘下移。然后通过挪移理想交叉口的位置，计算出不同挪移位置下，交叉口相对于理想绿波带上下边缘最大有效偏移量之和最小的一组，即为该理想信号距离下实际交叉口与理想信号最佳匹配位置，并计算绿波带宽。最后通过计算不同理想信号距离下的绿波带宽，获得最大绿波带宽下的最佳理想信号距离及公共周期，并根据实际交叉口与理想信号最佳匹配位置确定各交叉口相位差。

给定一条有n个交叉口的干道，编号分别为i=1,2，...，n，交叉口i的绿信比为λi，最大无效偏移率为ηi，最大无效偏移量为li，实际偏移量为xi，且相对理想绿波上下边缘有效偏移量分别为eupi与edowni，干线最初公共周期为C，理想信号距离为L，绿波带带宽为β，通过带速为v，最佳理想信号距离为Lopt最佳公共周期为Copt。算法步骤如下：

（1）找出干线交叉口最小绿信比λmin=min {λ1,λ2,...,λn}；

（2）计算各个交叉口的最大无效偏移率，ηi=λi-λmin（i=1,2，...，n）；

（3）确定理想信号距离L的范围（M为可调范围）；

（4）理想信号距离为L时，计算各交叉口最大无效偏移量li=Lηi（i=1,2，...，n）；

（5）交叉口1作为最初理想信号位置，计算各实际交叉口与相邻最近理想交叉口的实际偏差量xi(i=1,2,...,n)；

（6）计算实际交叉口相对于理想绿波上下边缘线的有效偏移量eupi与edowni（i=1,2，...，n），求出最大有效偏移量之和e=eupmax+edownmax，其 中eupmax=max {eup1,eup2,...,eupn}，edownmax=max {edown1,edown2,...,edownn}；

（7）将理想信号位置向右挪移一迭代步长（取10 m），返回（5），直到挪移量不小于理想距离L，求出并记录（6）中e值最小的一次emin，则所得绿波带为该理想信号距离下最大绿波带，绿波带宽占周期比为：β=ω-（ω为理想绿波带宽占周期的比，L为理想信号距离）；

（8）对L进行迭代（迭代步长一般取10 m），返回（4），求出（7）中β最大的一次下理想信号距离，即为理想信号最优距离Lopt；

（9）确定最终公共周期Copt=；

（10）根据最佳公共周期与实际交叉口与理想交叉口的最佳匹配位置确定相位差。

3 算例

3.1 基本数据

以干线道路为例，说明算法的应用。干线上有A、B、C、D、E、F、G、H共8个交叉口，相邻交叉口的距离依次为350、400、160、540、200、360、270 m，各交叉口主干道方向的绿信比分别为50%、70%、70%、34%、60%、36%、58%、64%，设定初始公共信号周期为80 s，通过带速度为36 km/h，理想交叉口间距范围为340～540 m，理想信号距离变化步长取10 m，干线交叉口如图3所示。

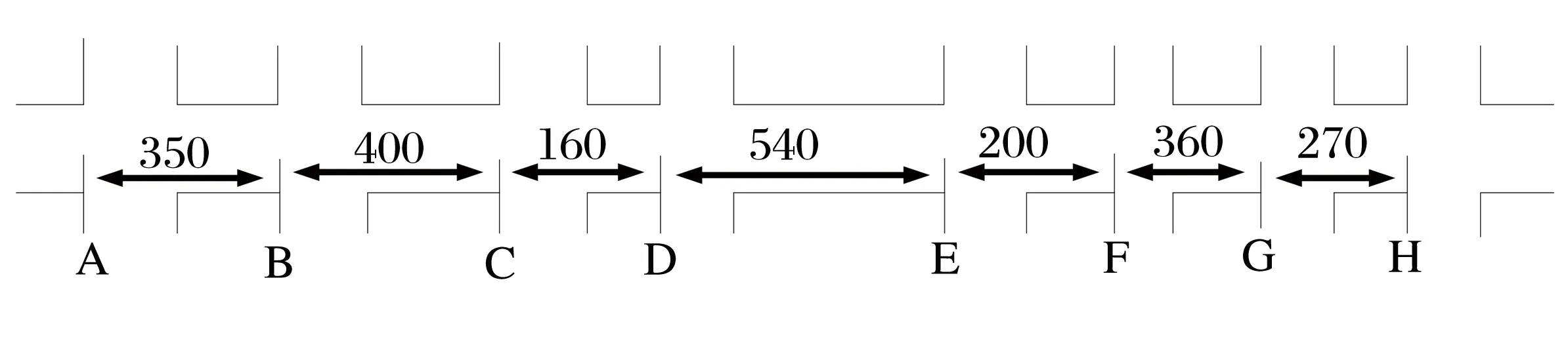
图3 干线交叉口（单位：m）

3.2 结果分析

用修正绿波带带宽的传统数解法与考虑无效偏移率数解法对案例分别进行求解，发现对于传统数解法，基于b值最大原则求解最优结果，当理想信号距离为370 m，公共周期为74 s，b值最大为170 m，确定的最优绿波带带宽为19%，而通过比较不同理想信号距离下传统数解法求得的绿波带带宽，发现在理想信号距离为420 m，公共周期为84 s，b值为140 m，获得最优绿波带带宽为22%。因此，传统数解法基于b值最大原则的择优方式存在缺陷，不同理想信号距离下的绿波带带宽如表1所示。

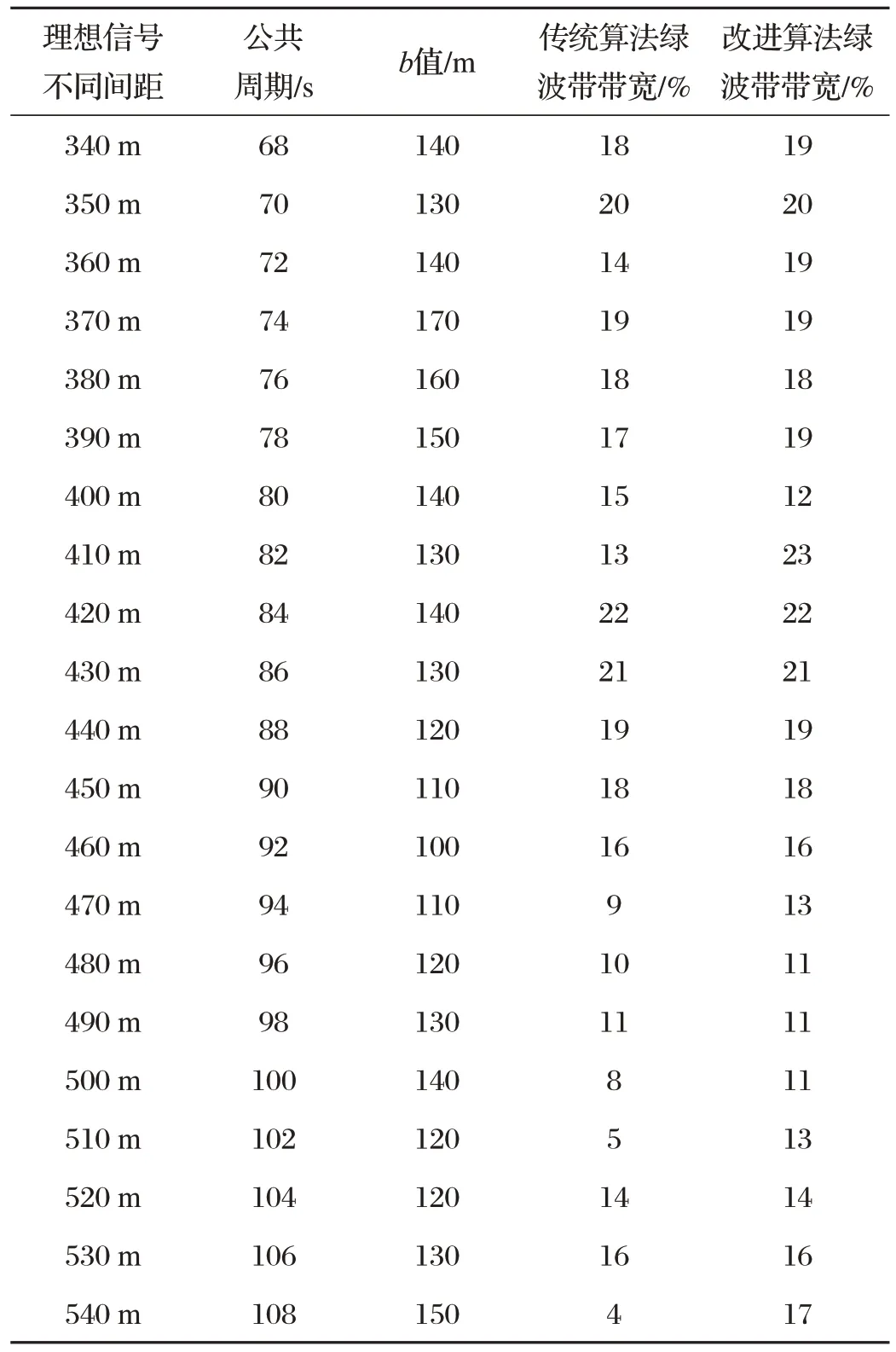
表1 不同理想信号距离下的绿波带带宽

通过对比改进后算法与传统数解法在不同理想信号距离下求得的绿波带带宽，发现改进后算法在一些特定理想信号距离下求得的绿波带带宽优于传统数解法求得的绿波带带宽，且改进后算法在理想信号距离为410 m，求得最大绿波带带宽为23%，而传统数解法实际在理想信号距离为420 m，获得最大绿波带带宽为22%，改进后算在该理想信号距离范围内求得最大绿波带宽同样优于传统数解法求得的最大绿波带宽，因此改进后算法更有利于获得干线协调控制下最大绿波带宽。不同理想信号距离下的绿波带带宽如图4所示。

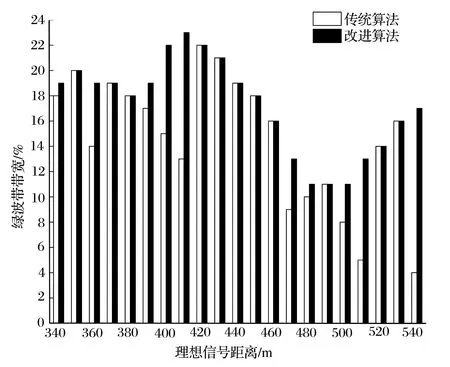
图4 不同理想信号距离下的绿波带带宽

3.3 最佳公共控制周期下的时距图

时距图用于反映干线协调控制下相邻交叉口间的相位差与采用该相位差的干线协调控制下实际的绿波效果，因此在干线各交叉口对称控制下实现双向绿波带宽的过程中，为说明改进后算法求得的绿波带宽与实际控制应用下绿波带宽相同，在理想信号距离为410 m、获得的最大绿波带宽为23%时，计算结果与时距图完全一致。时距分析图如图5所示。

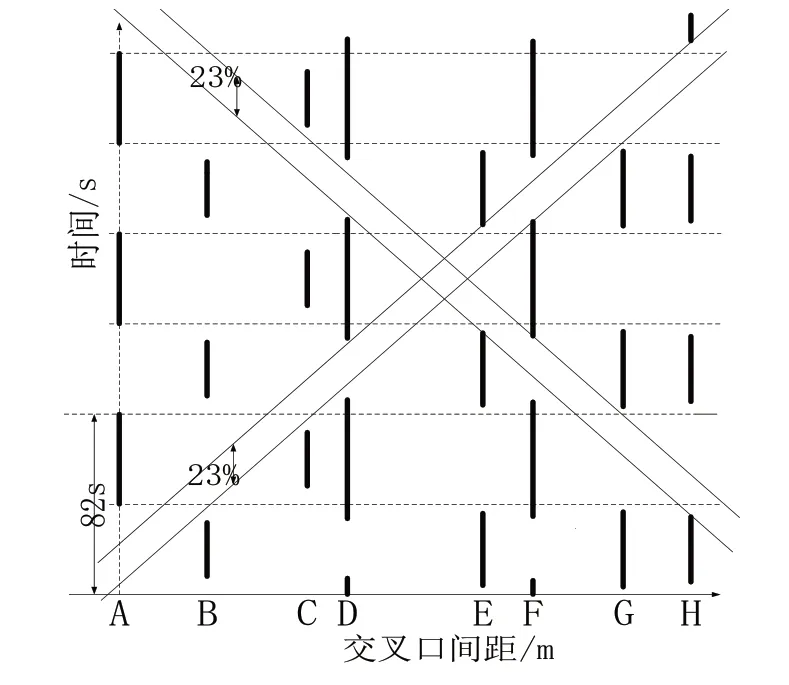
图5 时距分析图

3.4 交叉口最优相位差设置

经典数解法中，交叉口相位设置按实际交叉口与挪移最近的理想交叉口采用相同控制设计原则，对理想交叉口按顺序进行编号，对靠近奇数编号理想交叉口的所有实际交叉口采用同步协调控制，对靠近偶数编号理想交叉口的所有实际交叉口也采用同步协调控制，对靠近奇数与偶数的两组交叉口采用交互协调控制，求得实际交叉口与最佳理想交叉口位置关系图，依据经典数解法相位差设置原则，交叉口A、C、D、F采用同步式控制，交叉口B、E、G、H亦采用同步式控制，两组同步式交叉口采用交互式控制。本文采用文献[17]提出的相位差设计原则，在对该算法求得最优绿波带宽不发生改变的前提下，各实际交叉口的相位差可依据左右理想交叉口信号为基准，根据需要灵活设置。

两种算法分别求得了在实现干线最大绿波带宽下的相邻交叉口间最优相位差，对比发现改进后算法获得的最大绿波带宽优于传统数解法获得的最大绿波带宽。因此改进后算法求得的各交叉口间相位差优于传统算法求得的各交叉口间相位差，实际交叉口位置与最佳理想交叉口位置的相对距离如图6所示，交叉口间的最优相位差如表2所示。

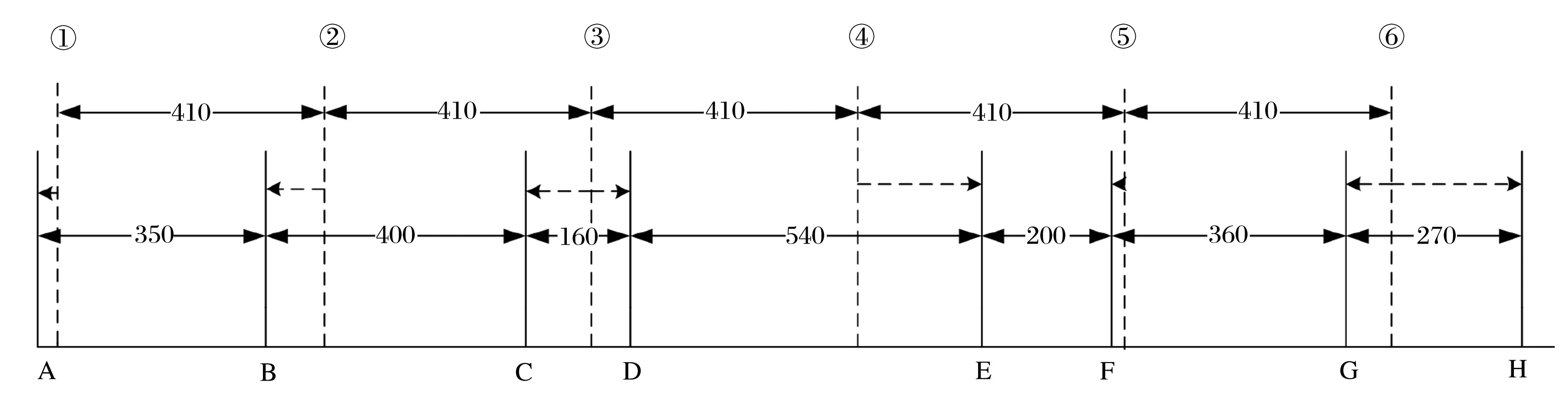
图6 实际交叉口位置与最佳理想交叉口位置的相对距离（单位：m）

表2 交叉口间的最优相位差

4 结语

为使绿波带宽的计算更为准确，本文提出了交叉口无效偏移率与交叉口有效偏移量的概念，通过计算交叉口相对理想绿波带上下边缘线的有效偏移量，修正了以往研究在实际绿波带的上边缘高于理想绿波带的上边缘，或实际绿波带的下边缘低于理想绿波带的下边缘的情况下，绿波带宽的计算误差，并提出了考虑交叉口无效偏移率的数解算法。

算例计算结果表明，改进后的数解算法在理想信号距离范围内，获得了最大的绿波带带宽及最佳公共控制周期，其结果优于传统数解算法，且在不同理想信号距离下求得的绿波带带宽同样优于传统数解算法求得的绿波带带宽，因此改进后算法较传统数解算法应用于干线双向绿波设计更为有效。

但本文提出的基于交叉口无效偏移率的数解算法只考虑了干线协调对称控制的情况，对于干线非对称协调控制还需在本文基础上做进一步研究。