基于最大纠缠｜χ〉态的量子信息集中

张玉春， 柏明强， 柳人菊， 吴 帆

（四川师范大学 数学科学学院，四川成都610066）

根据量子不可克隆定理［1］，一个未知的量子态不能被精确克隆，使得克隆态与初始态完全相同.那么考虑是否可以进行近似精确的克隆呢？基于这样的问题，Buzek等［2］在1996年首次提出量子克隆的概念.量子克隆可以将一个未知态的信息以某些概率分布到更大的系统中.将量子克隆与隐形传态相结合，Murao等［3］提出了量子远程克隆.

作为量子远程克隆的逆过程，2001年Murao等［4］首次提出了远程量子信息集中的概念.他们以一个四粒子非束缚纠缠态作为量子信道，仅通过局域操作就可将分布于空间分离的三方的量子信息集中回单粒子态.从此，一些学者开始这方面的研究.2003年Yu等［5］利用四粒子GHZ态完成了优化1→2的通用远程克隆之逆.此后，远程量子信息集中被推广到多粒子和高维系统中［6-7］.不同于以往主要关注最优通用远程克隆之逆，Wang等［8］2013年提出了辅助自由相位协变克隆之逆的量子远程信息集中.其主要思想是利用非对称W态，将通过一个辅助自由相位协变克隆机而分布于空间分离的两方的量子信息集中回单粒子态.同年Bai等［9］提出了优化非对称经济1→3相位协变克隆之逆.2014年，Peng等［10］提出了优化通用1→2的任意两粒子量子信息集中协议.2016年，Wang等［11］提出了增加控制方的量子信息集中方案.

现有成果中，量子信道大多选用GHZ态［5，9，11-12］、W态［13-15］、Cluster态［16-17］等.到现在为止却缺少用｜χ〉态作为量子信道来完成量子信息集中的研究.而Wu等［18］证明了｜χ〉态比GHZ态、W态及Cluster态具有更好的纠缠性质.Wang等［19］证明｜χ〉态很难被局部操作摧毁，具有很好的鲁棒性.基于以上考虑，选择｜χ〉态作为量子信道完成量子信息集中是有意义的.

1 量子远程信息集中

1.1 1→3的相位协变量子远程克隆假设通过优化非对称经济1→3相位协变量子克隆机［20］后，一个未知赤道态

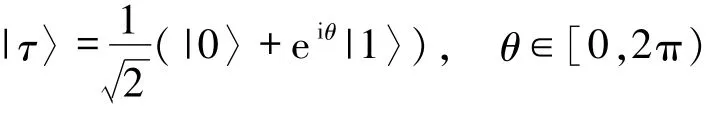
的信息被加载到由粒子A、B和C构成的克隆态.

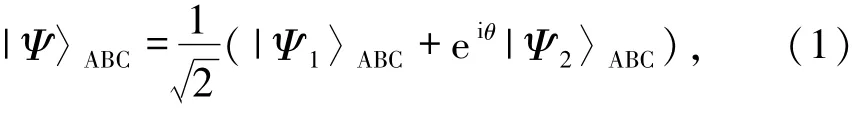
其中，粒子A、B、C分别属于空间分离三方Alice、Bob和Charlie.并且态｜Ψ1〉ABC和｜Ψ2〉ABC被定义如下：

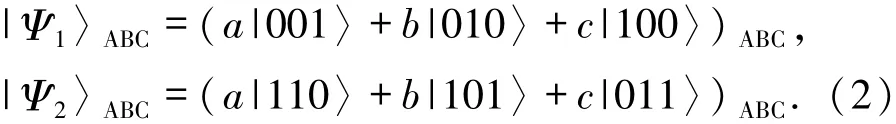
系数a、b和c满a2+b2+c2＝1且a，b，c≥0.

1.2 以纠缠χ态为信道的远程信息集中考虑四粒子纠缠｜χ〉态

作为量子信道，将态｜Ψ〉ABC的信息集中回到一个单粒子态｜τ〉D，即｜Ψ〉ABC→｜τ〉D.这里粒子1、2、3、D分别属于Alice、Bob、Charlie和David（David是量子信息｜τ〉D的恢复方）.于是整个系统为

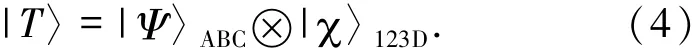
利用Bell基系统总态｜T〉可以表示为

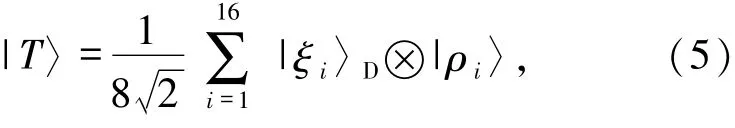
其中

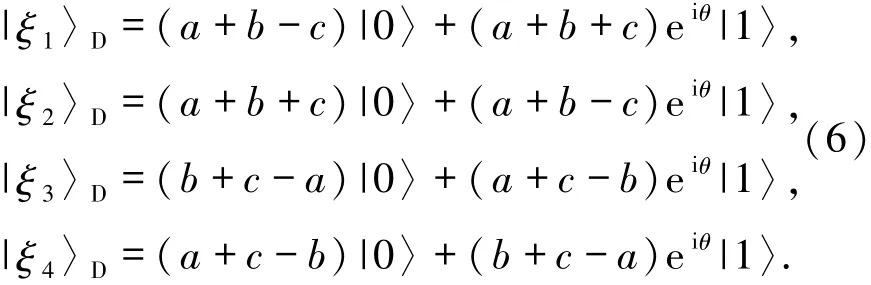
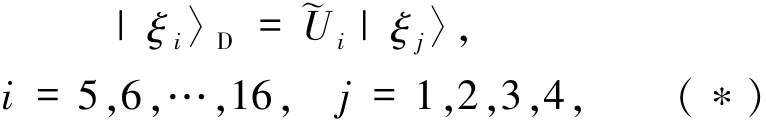
而˜Ui是酉操作，具体关系及酉操作˜Ui见表1.

表1 ｜ξi〉D（i＝1，2，…，16）与｜ξj〉D（j＝1，2，3，4）的关系Tab.1 Relationship between｜ξi〉D（i＝1，2，…，16）and｜ξj〉D（j＝1，2，3，4）

（5）式中

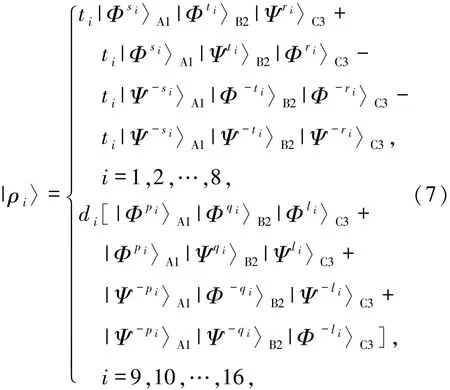
其中

（7）式中i＝1时s1＝1，t1＝-1，r1＝-1.则｜ρ1〉的第一项｜Φ1〉A1｜Φ-1〉B2｜Ψ-1〉C3也即｜Φ+〉A1｜Φ-〉B2｜Ψ-〉C3具体指Alice、Bob及Charlie对各自的粒子对执行Bell测量｜Φ+〉A1、｜Φ-〉B2、｜Ψ-〉C3.其他测量情况类似.在此之后，他们需要将自己的测量结果以经典通信的方式告诉David.根据（5）式，一旦三方实施联合Bell测量，总系统就会坍缩成

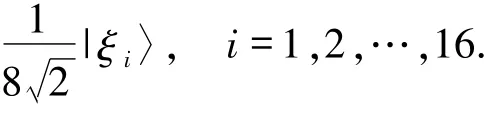
信息恢复方David再对粒子D按表1执行适当的酉操作，｜ξi〉（i＝1，2，…，16）就可以转化为｜ξi〉（i＝1，2，3，4）之一.因此，只需要针对

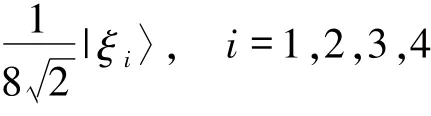
进行讨论.

假设，Alice、Bob及Charlie联合测量结果为｜Φ+〉A1｜Φ-〉B2｜Ψ-〉C3，那么系统的态将坍缩为

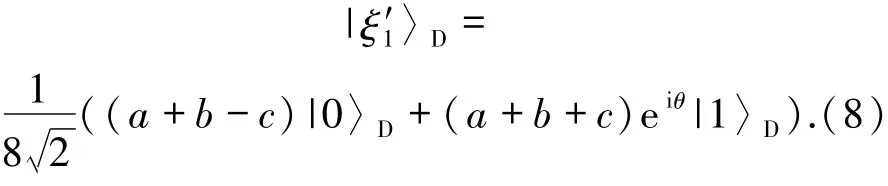
忽略全局因子并将其归一化得到

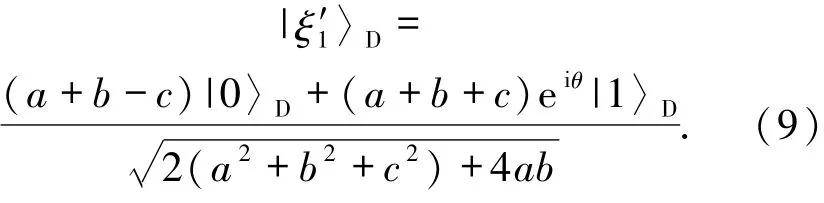
为重构原始态，David引入一个处于基态｜0〉D′的辅助粒子D′，从而粒子D和D′构成的复合态为

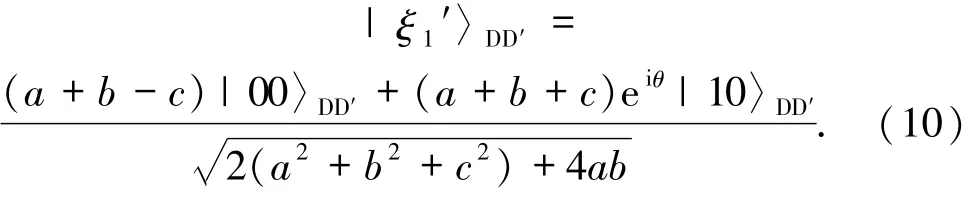
接下来，用2种不同的测量方法来恢复初始量子态，即重新构建初态

1.2.1利用投影测量来进行量子信息集中 本小节主要利用投影测量来完成量子信息集中，并对系数a、b、c做2种情况的讨论.

第一种情况：c≥0，a≥b，则（a+b+c）≥（a+b-c），（a+c-b）≥（b+c-a）.

为了恢复初始量子信，David选择适当的酉变换U1如下：

然后，在基｛｜00〉、｜01〉、｜10〉、｜11〉｝DD′下对粒子DD′施行酉运算U1.这样，粒子D和D′的态变成

David再对辅助粒子D′进行投影测量：如果测量结果为｜0〉D′，则原始态被恢复，成功的概率为

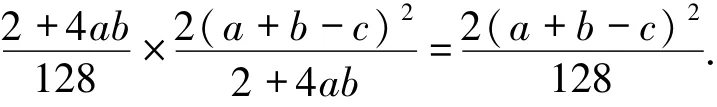
若测量结果为｜1〉D′，则信息集中失败.

若联合Bell测量后系统塌缩为

David选择酉变换U2、U3、U4，用类似方法就能恢复原始态，U2、U3、U4如下

表2 坍缩态｜ξi〉D（i＝1，2，…，16）及执行的酉操作和UiTab.2 Collapse state｜ξi〉D（i＝1，2，…，16）and unitary operationand Ui

表2 坍缩态｜ξi〉D（i＝1，2，…，16）及执行的酉操作和UiTab.2 Collapse state｜ξi〉D（i＝1，2，…，16）and unitary operationand Ui

｜ξi〉D 需在｜ξi〉D上执行的˜U+i投影测量阶段U i｜ξi〉D，i≡1（mod 4） ˜U+i U 1｜ξi〉D，i≡2（mod 4） ˜U+i U2｜ξi〉D，i≡3（mod 4） ˜U+i U3｜ξi〉D，i≡0（mod 4） ˜U+i U 4

整个方案成功的概率为

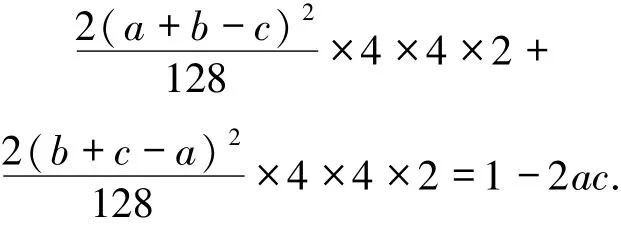
第二种情况：c≥0，a＜b，则（a+b+c）＞（a+b-c），（a+c-b）＜（b+c-a），采用与上面一样的方法就可以完成信息集中.其中相应的酉算子如下：

整个方案成功的概率为

1.2.2利用POVM测量来进行量子信息集中

POVM测量又称为半正定算子值测量，常被用于概率性量子信息任务处理中.与投影测量相比，POVM测量要更为简单，后者算子的矩阵阶数是前者的一半，并且也不需要再满足算子之间的正交性.基于此，考虑用POVM测量来完成信息集中任务.以｜ξ′1〉DD′为例，其余情况类似.David对粒子对（D，D′）执行受控非门.其中粒子D为控制粒子，而粒

子D′为目标粒子.从而｜ξ′1〉DD′变为

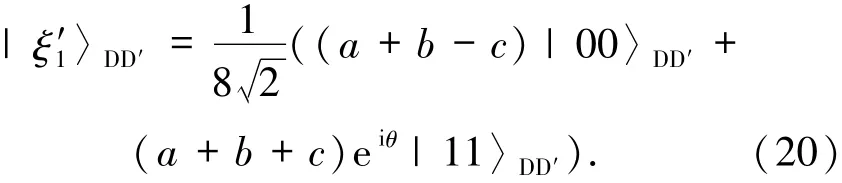
为了恢复初始量子信息，｜ξ′1〉DD′可以改写为

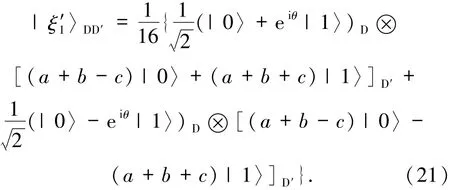
David需要对辅助粒子D′执行某适当测量获得态

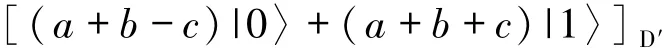
和［（a+b-c）｜0〉-（a+b+c）｜1〉］D′.通常情况下，这二者不正交，因此不能确定性区分.但可以使用POVM测量概率性地对二者加以区分.POVM算子取下列形式，对于系数的讨论，也分2种情况.

第一种情况：c≥0，a≥b，则（a+b+c）≥（a+b-c），（a+c-b）≥（b+c-a），则

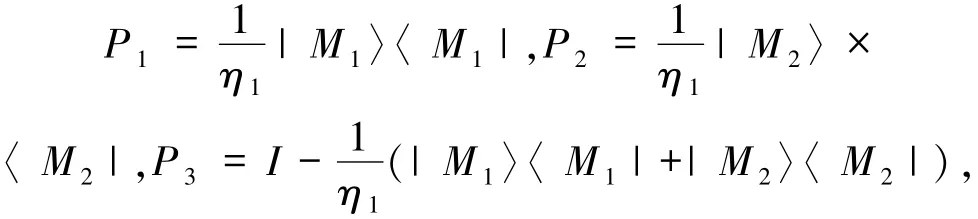
其中

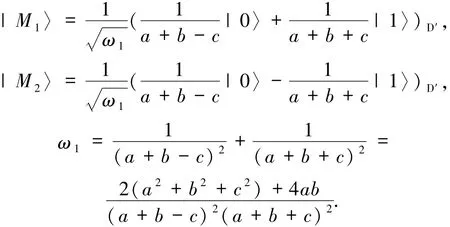
I为恒等算子，与a、b、c密切相关的参数η1应确保P3为半正定算子，参数η1必须满足

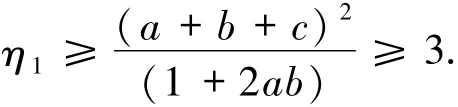
3个算子可以写成下列矩阵形式：执行POVM测量后，David能以如下概率获得P1和P2，

利用POVM测量David一定能确定粒子D′的态.而以概率David可以得到P3的值，但不能确定粒子D′的态.一旦David确定了

或

就意味着知道了态

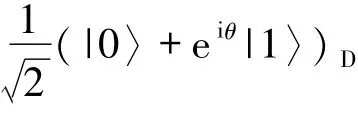
或

表3 坍缩态｜ξi〉D（i＝1，2，3，4）与执行POVM测量的相关参数Tab.3 Collapse state｜ξi〉D（i＝1，2，3，4）and parameters related to POVM measurement

从而整个方案成功的概率为

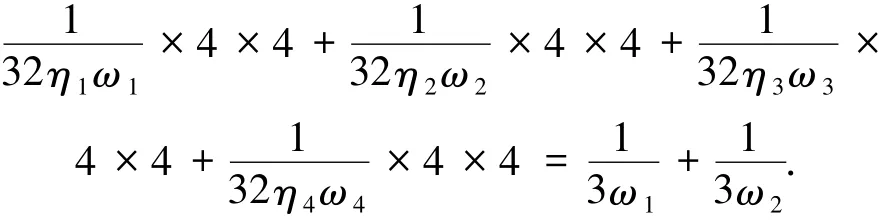
第二种情况：若c≥0，a＜b，则

采用与上面一样的方法就可以完成信息集中，其相关参数的取值与表3一样.整个方案成功的概率为

关于上述方案的物理实现问题，主要考虑以下4点：1）四粒子最大纠缠｜χ〉态的准备，文献［21］给出了一个任意四粒子｜χ〉态的联合远程制备方案.2）Bell态测量，文献［22-23］中关于原子和光量子的Bell测量已经能被物理实现.3）POVM测量，文献［24］表明在一定辅助条件下POVM测量能被物理实现.4）投影测量，文献［25］证明利用Bell基投影测量可以物理实现.基于这些已有的研究，此方案在物理上是可行的.

2 安全性分析

假设在方案中存在不诚实的参与者（不妨是Alice），她打算单独安全地重构原始态而不需要其他参与者帮助.这种内部窃听比外部窃听更有力，因为窃听者合法地知道部分信息.在量子信息集中过程中，Alice、Bob、Charlie三者需要对自己的粒子对执行Bell测量，并将测量结果以经典通信的方式发送给David.在经典信息的发送过程中，窃听者可以窃听消息而无法篡改它们，因此存在经典信息泄露的可能.但在本方案中，这种经典信息的泄露也无法使得Alice的窃听成功.假设Alice窃取到经典信息并以的概率猜测到某次测量中Bob和Charlie的测量结果均为｜Φ+〉，此时Alice和David的联合态形式为：

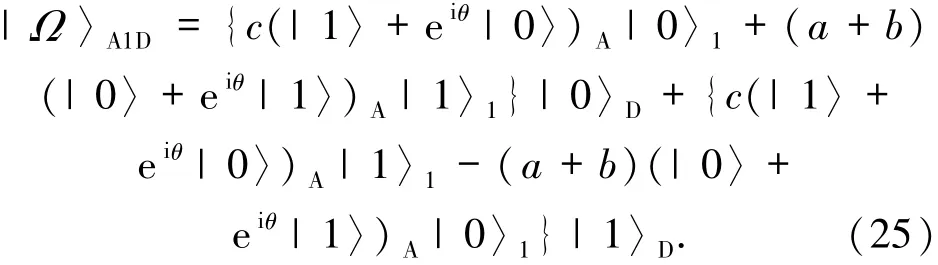
由于粒子D是纠缠信道中的粒子，这使得如果David不对自己拥有的粒子进行测量并向Alice公布测量结果，那么Alice将无法单独地重构原始态，从而窃听失败.因此Alice采用第二种方法，把一个初态为｜0〉的辅助粒子E与信道中Bob或Charlie的粒子进行纠缠（不妨是Bob），然后测量辅助粒子来窃取信息.Alice执行CNOT操作将2粒子与E粒子进行纠缠，2粒子为控制粒子，E粒子为目标粒子，这样纠缠后的信道为

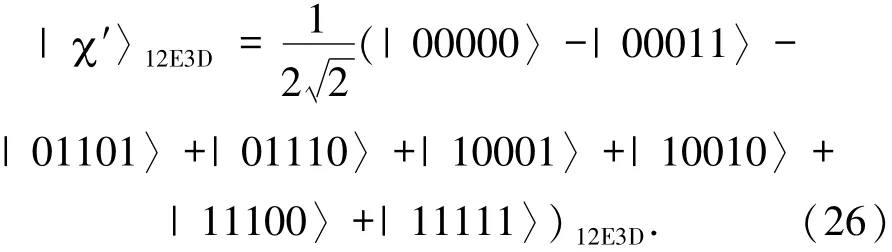
系统总态｜T′〉＝｜Ψ〉ABC⊗｜χ′〉12E3D.当Alice、Bob、Charlie执行联合测量｜Φ+〉A1｜Φ+〉B2｜Φ+〉C3后，粒子E和D塌缩为

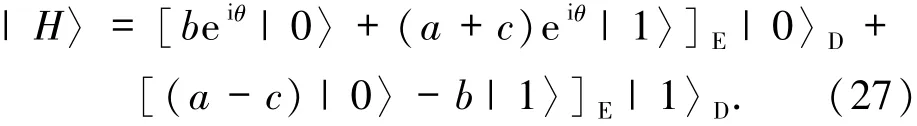
（27）式中粒子D和E处于纠缠状态，但不管David对自己的粒子做什么测量，Alice都无法通过粒子E获得完整的信息，窃听失败.综上所述，本方案是安全的.

3 结论

以四粒子最大纠缠｜χ〉态作为量子信道，在优化非对称经济1→3相位协变量子克隆的基础上提出了一种量子信息集中方案.分别采用投影测量和POVM测量将信息集中回单粒子态，并对整个方案成功的概率做了讨论.通过计算发现采用不同的测量方法成功的概率不一样，方案成功的概率都依赖于克隆态的系数.最后对方案实验的可行性和安全性进行了分析，发现方案在物理上是可以实现的并且是安全的.