基于Lyapunov范数的线性斜积半流非一致指数二分性的离散Datko型定理

岳 田， 宋晓秋

（1.湖北汽车工业学院理学院，湖北十堰442002； 2.中国矿业大学 数学学院，江苏徐州221116）

众所周知，近年来关于微分系统定性理论的研究取得了突破性的进展，尤其是在指数渐近行为方面，大量公开问题的解决，使得相关理论不断拓展和完善［1-12］.1930年，Perron［1］在有限维空间中利用“输入-输出”方法（又称Perron方法或测试函数方法）建立了齐次微分方程˙x（t）＝A（t）x（t）的解的指数渐近行为（指数二分性）与对应的非齐次微分方程˙x（t）＝A（t）x（t）+f（t）之间的联系.随后，Massera等［2］在其基础上，将其结果扩展到了无限维空间的情形，并首次研究了相应微分系统的非一致指数渐近行为.2010年，Barreira等［3］通过定义合适的范数（又称Lyapunov范数），讨论了演化过程非一致指数稳定性与容许性之间的联系.此后，通过Lyapunov范数来获取非一致指数渐近行为（指数稳定性、指数膨胀性、指数二分性、指数三分性）成为了一个重要的技术手段，如文献［4］针对具有非一致指数增长的演化族，研究了其非一致指数二分性与函数空间对（Lp（X），Lq（X））的容许性之间的联系，获得了刻画非一致指数二分性的Perron型结论；文献［5］对于非一致指数增长的半流上的强连续上闭链给出了非一致指数二分性存在的容许性条件.

作为C0半群、演化算子、演化过程的推广，由半流和上闭链构成的线性斜积（半）流，是动力系统渐近行为分析方面的一类重要工具.如文献［6］借助稳定性理论中的Datko-Pazy型方法［7-9］，讨论了斜积半流一致指数稳定的特征，建立了其一致指数稳定的若干充要条件；文献［10-11］基于Lyapunov范数将Datko相关经典结论扩展到了线性斜积半流，分别给出了其非一致指数稳定与非一致指数二分的Datko型条件的连续型刻画.

受文献［11］的启发，从已知的连续型特征出发，本文将基于Lyapunov范数建立Banach空间中刻画线性斜积半流非一致指数二分的Datko型条件的离散形式，给出若干充要条件，所得结论推广了指数稳定性与指数二分性理论中一些已有结果（如Datko、Pazy、Preda等）.

1 预备知识

设X是一个Banach空间，Θ是一个度量空间，将空间X上的范数及作用其上面的有界线性算子全体B（X）上的范数记作‖·‖.记I为单位算子，［a］表示不超过实数a的最大整数，M（R+，X）表示所有从R+到X的Lebesgue可测函数构成的集合.

定义1.1［5，10-11］称映射σ：Θ×R+→Θ，（θ，的线性连续半流，如果满足

（i）σ（θ，0）＝θ，∀θ∈Θ；

（ii）σ（θ，t+s）＝σ（σ（θ，s），t），∀t，s≥0，θ∈Θ；

定义1.2［5，10-11］设σ为Θ上的线性连续半流，称算子值函数Φ：Θ×R+→B（X），（θ，t）Φ（θ，t）为具有（非）一致指数增长的强连续上闭链，如果满足

（i）Φ（θ，0）＝I，∀θ∈Θ；

（ii）对每个θ∈Θ及x∈X，Φ（θ，·）x连续；

（iii）Φ（θ，t+s）＝Φ（σ（θ，t），s）Φ（θ，t），∀t，s≥0，θ∈Θ；

（iv）∃ω∈R及M：Θ→R+使得对∀t≥0，θ∈Θ有‖Φ（θ，t）‖≤M（θ）eωt.

注1.1［5，10-11］若，则称Φ具有一致指数增长性.

称ε＝X×Θ上的动力系统π＝（Φ，σ）为线性斜积半流［5，10-11］，其中

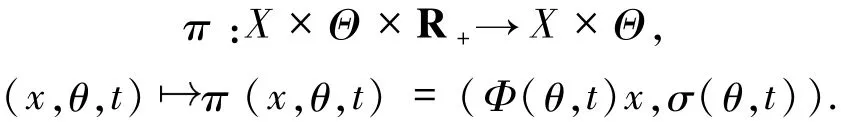
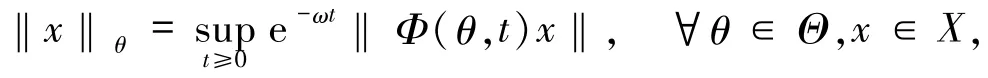
设π＝（Φ，σ）为一具有（非）一致指数增长的线性斜积半流，记易知为定义在X上的一个范数（即Lyapunov范数，详见文献［5，10-11］），且满足

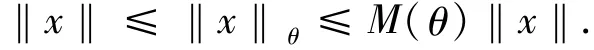
注1.2［5，10-11］对∀θ∈Θ，x∈X，t≥0，有

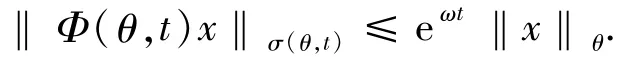
对每个p∈［1，∞］，记

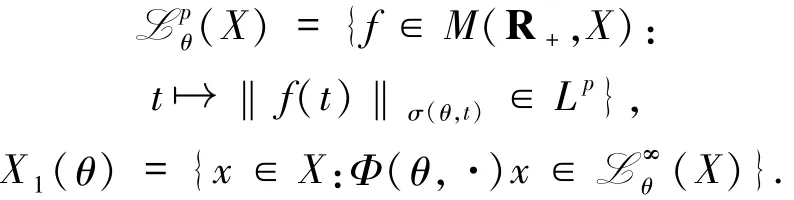
为了同文献［11］保持连贯，本文将作相同假定：X1（θ）是闭的，且存在一个闭子空间X2（θ）使得X＝X1（θ）⊕X2（θ）.P1（θ）、P2（θ）为两个投影族，并满足Pi（θ）（X）＝Xi（θ），i＝1，2.

定义1.3［5，11］称线性斜积半流π＝（Φ，σ）为非一致指数二分的，如果存在常数N1，N2，v＞0，使得

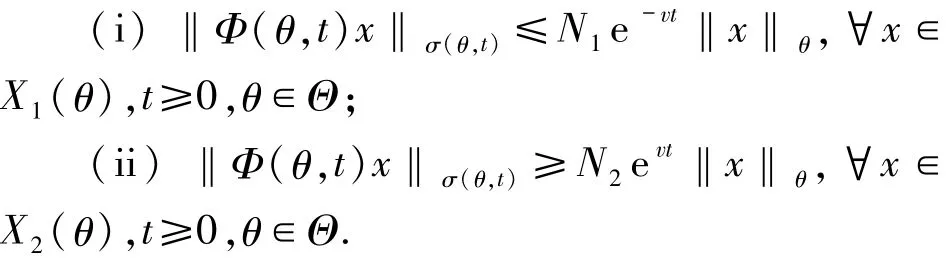
注1.3在定义1.3中，若P2（θ）＝0，则称线性斜积半流π＝（Φ，σ）为非一致指数稳定的［10］；若P1（θ）＝0，则称线性斜积半流π＝（Φ，σ）是非一致指数膨胀的.

引理1.1［11］如果对所有的θ∈Θ及t≥0有

则线性斜积半流π＝（Φ，σ）是非一致指数二分的，当且仅当存在常数p，K，m＞0使得

采用类似于文献［12］中定理3.1的证明方法，可得引理1.2.

引理1.2如果对所有的θ∈Θ及t≥0有

则线性斜积半流π＝（Φ，σ）是非一致指数二分的，当且仅当存在常数p，K＞0使得

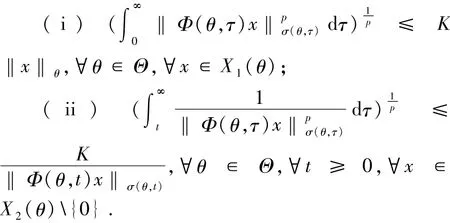
注1.4若将引理1.1与引理1.2中的条件

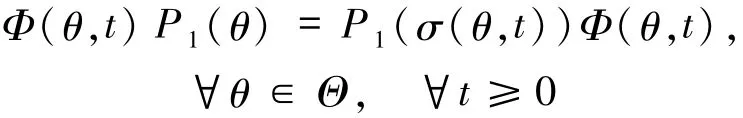
去掉，则后面相应的关系式仅为线性斜积半流π是非一致指数二分的充分条件，如文献［11］中的定理

3.1.

2 主要结论

定理2.1如果对所有的θ∈Θ及t≥0有

则线性斜积半流π＝（Φ，σ）是非一致指数二分的，当且仅当存在常数p，K′＞0使得

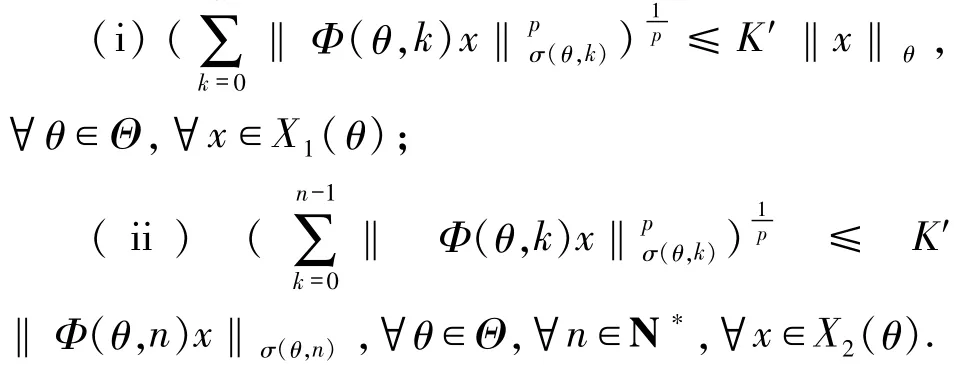
证明必要性 若线性斜积半流π＝（Φ，σ）是非一致指数二分的，则利用定义1.3可得，对∀θ∈Θ，∀x∈X1（θ）有

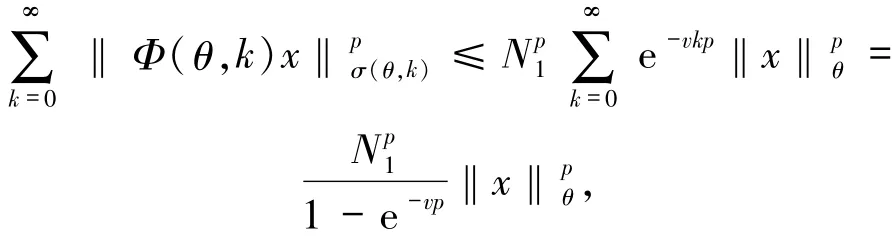
从而

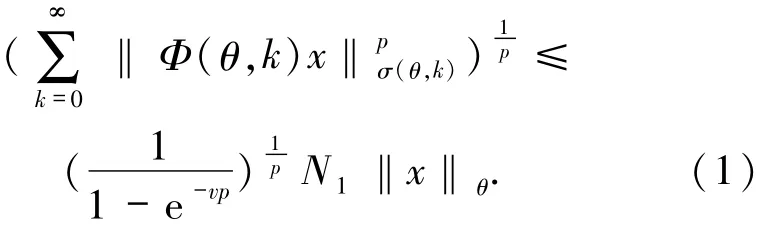
另一方面，借助定义1.3以及

的事实，可得对于∀θ∈Θ，∀n∈N*，∀x∈X2（θ）以及k∈｛0，1，…，n｝，有

进而，

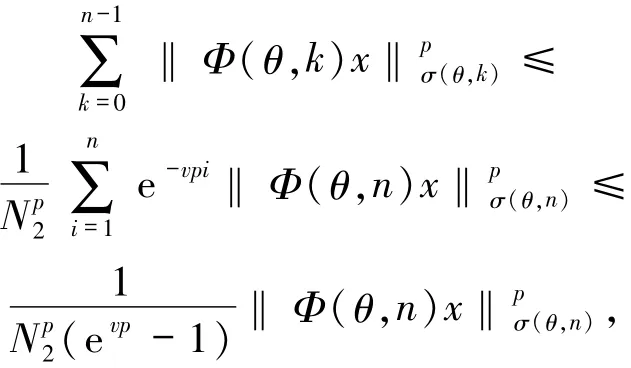
故有

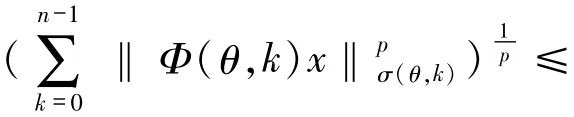
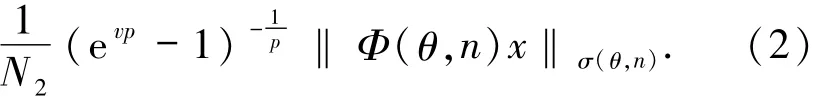
根据（1）与（2）式，取

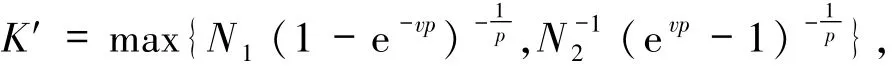
可得结论成立，其中N1、N2、v详见定义1.3.

充分性 设θ∈Θ，x∈X1（θ），由于

故有

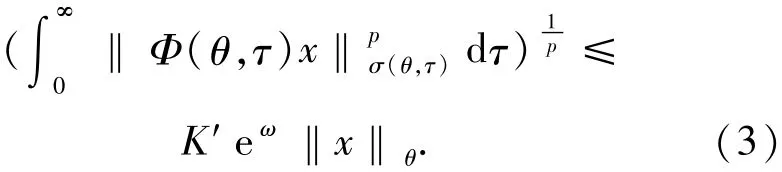
设θ∈Θ，x∈X2（θ）.记

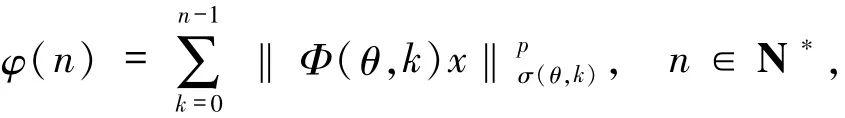
则由条件（ii）有

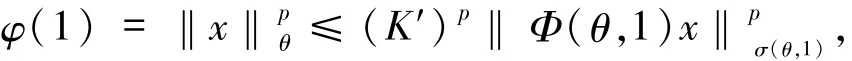
进而

另一方面，

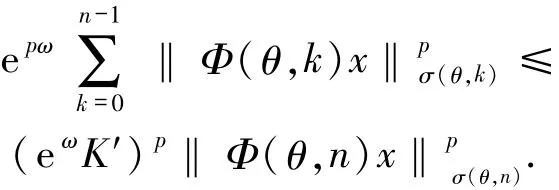
故对∀t≥0有

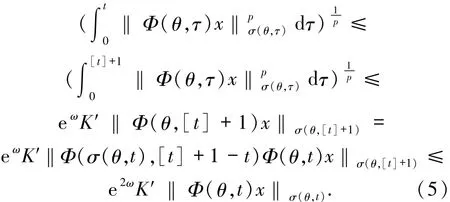
根据（3）-（5）式，取K＝e2ωK′，m＝1／K′，可得引理1.1中的条件（i）-（iii）成立，故线性斜积半流π＝（Φ，σ）是非一致指数二分的.

定理2.2如果对所有的θ∈Θ及t≥0有

则线性斜积半流π＝（Φ，σ）是非一致指数二分的，当且仅当存在常数p，K′＞0使得

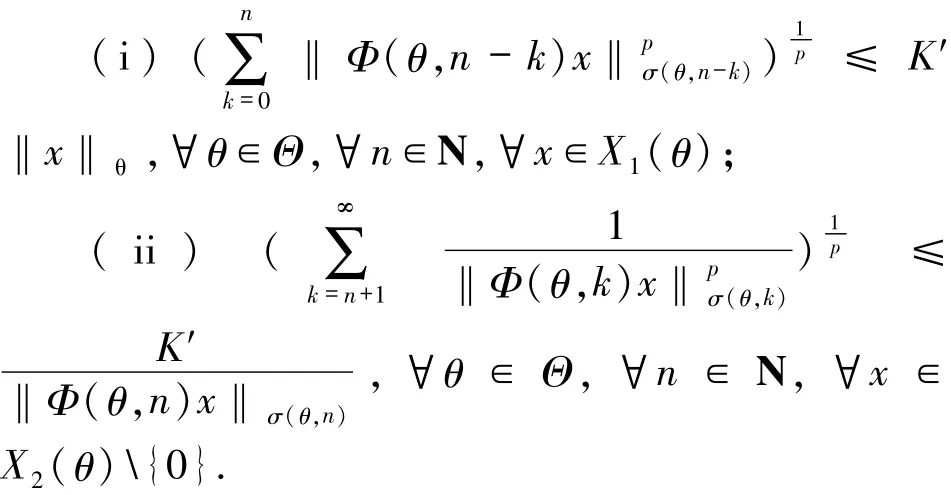
证明必要性 显然.类似定理2.2的讨论可得关系式（i），基于

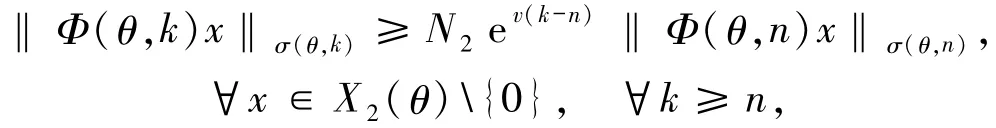
可得关系式（ii）成立.

充分性 设θ∈Θ，x∈X1（θ），则由条件（i）有

从而类似于定理2.1中的讨论，可得（3）式成立.

设θ∈Θ，x∈X2（θ）＼｛0｝，t≥0.记m＝［t］，则

进一步地，

这意味着

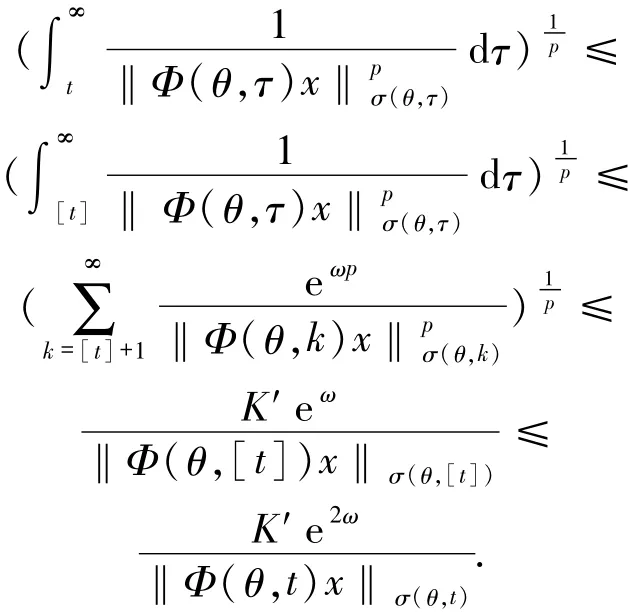
故借助引理1.2可得线性斜积半流π＝（Φ，σ）是非一致指数二分的.

致谢湖北汽车工业学院学生工作研究重点项目（2020XGYJ06）和湖北汽车工业学院党的十九届四中全会精神研究阐释专项课题（No.8）对本文给予了资助，谨致谢意.