一类随机微分变分不等式

山述强， 王中宝

（1.西南民族大学数学学院，四川成都610041； 2.西南交通大学数学学院，四川成都611756）

假设K是Rn的闭凸子集，f：R×Rm×Rn→Rm和g：R×Rm×Rn→Rn是两向量值函数.有限维空间中的变分不等式可以表述为：对几乎所有的t∈［0，T］，找（xt，μt）满足

其中Sol（K，g（t，xt，·））表示动态变分不等式的解集.

对于问题（1），2008年Pang等［1］考虑它的Carathédory弱解，即找（xt，μt），其中xt是一绝对连续函数，μt是一可积函数，使得微分方程对几乎所有的t成立；2009年Pang等［2］找到了在初值条件下微分变分不等式的解.在此基础上，Han等［3］研究了一类非芝诺微分拟变分不等式；Stewart［4］研究了微分变分不等式解的唯一性；Pang等［5］介绍了强正则微分变分系统；Wang等［6］研究了有限维的微分向量变分不等式；Li等［7］研究了有限维空间中的微分混合变分不等式；Friesz等［8］研究了托运人动态寡头垄断网络竞争，并将其转化为微分变分不等式；Li等［9］研究了有限维空间中的微分逆变分不等式；还有许多数学工作者也关注了微分变分不等式［10-19］.

然而现实中的许多问题总是会受到一些不确定因素的影响.为了刻画出这些影响，随机微分变分不等式变得非常重要.

假设Rm和Rn为两实欧氏空间，其范数为内积为·〉Rn.假设K是Rn中的闭凸子集，（Ω，F，P）为一概率空间，Bt是标准的n-维布朗运动.假设｛Ft｝是由Bt生成的σ-域，即Ft＝σ｛Bs；0≤s≤t｝.令ξ为一Rm-值的F0可测随机变量.一般来说，假设｛Ft｝是右连续的，且满足通常假设.随机微分变分不等式（简写为SDVI）可以表述为：找（x（t，ω），μ（t，ω））满足

其中“a.s.”表示在dt×dP下几乎确定成立，Sol（K，ψ（t，ω，x（t，ω），·））表示下面的随机动态变分不等式的解集：找μ（t，ω）∈K，满足

2013年，Gwinner［20］介绍了一类新的微分变分不等式，并证明了动态变分不等式与动态投影系统等价.受上述工作影响，本文将研究随机微分变分不等式，并找到其适定解.

1 预备知识

下面介绍一些定义、假设和引理.

1）对于i＝m，n，记H2（［0，T］，Ri）（简记为为所有的R-值Ft-可测过程，即i

2）定义集合K如下：

注1.1对于任意的i＝m，n，H2（（0，T），Ri）为一Hilbert空间，其内积为

引理1.2K为H2（（0，T），Rn）中的闭凸子集.

证明假定μ1，μ2∈K，即

和对几乎所有的

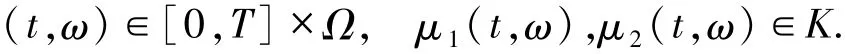
对任意的0＜λ＜1，容易验证

和

因此，对任意的0＜λ＜1，

所以K为闭凸子集.

假定μn∈K为H2（［0，T］，Rn）的函数列，且μn→μ*，即

那么存在子函数列μn k满足

因为K是闭集，则有

即K是闭集.证毕.

以下记x（t，ω）和μ（t，ω）分别为xt和μt.

假设1.3对于∀（x，μ）∈Rm×Rn，函数ψ（·，·，x，μ）：［0，T］×Ω×Rm×Rn→Rn满足ψ（·，·，x，μ）∈H2（［0，T］，Rn），且存在正实数c使得下式成立

因此可以定义映射Ψ如下：

引理1.4如果假设1.3成立，那么Ψ为从H2（［0，T］，Rm）×H2（［0，T］，Rn）到H2（［0，T］，Rn）的映射.

证明对于任意给定的

由假设1.3可知

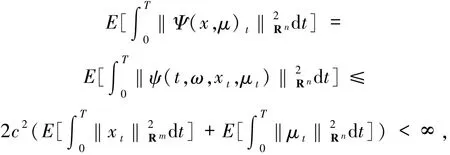
即

证毕.

假设1.5对于任意的（x，μ）∈Rm×Rn，

且对于

存在正实数c1＞0满足

注1.6由假设1.5可知，对于所有的

假设1.7Ψ是强单调的，即存在实数c2＞0且满足

有

由引理1.2可知，上述的随机动态变分不等式可以表述为：找μ*∈K满足

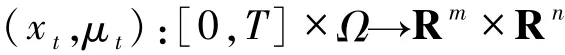
定义1.8称函数对统（2）的适定解，当且仅当

为系满足

注1.9随机动态变分不等式等价于下述随机动态投影系统

其中，ρ＞0为一正实数，PK为K→K的投影.由此可知，随机微分变分不等式可以改写为：找函数对

满足

2 随机微分变分不等式解的存在性与唯一性

下面将应用压缩映射原理找出系统（5）的解，并得到其解是唯一的.

考虑空间H2（［0，T］，Rm）×K，其内积为

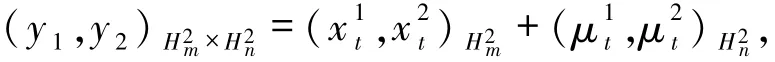
引理2.1假设E［｜ξ｜2］＜∞和A2＝1-2ρc2+ρ2c1＜1.如果假设1.3、1.5和1.7成立，那么Φ为从H2（［0，T］Rm）×K到H2（［0，T］，Rm）×K的映射.

证明由引理1.2可知，K为H2（［0，T］，Rn）中的闭凸子集.对于任意的

可知

这表明PK（μt-ρΨ（xt，μt））是非空的，且满足

另一方面，有

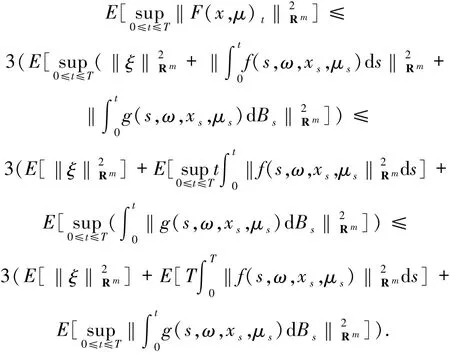
由Doob不等式，可知

由假设1.5和E［｜ξ｜2］＜∞，可知

因此

证毕.

由引理2.1可知，希望Φ为H2（［0，T］，Rm）×K中的压缩映射，一般来说，这个不成立，但是有下面的定理.

定理2.2假设

其中c1、c2为假设1.5和假设1.7给定的实数.如果假设1.3、假设1.5和假设1.7成立，则算子Φ为H2（［0，T］，Rm）×K到H2（［0，T］，Rm）×K的压缩映射，并且存在唯一的（xt，μt）满足系统（5）.

证明由假设1.3、假设1.5和假设1.7可知，对任意的

有

因此

另一方面，由假设1.7可知

结合范数

的定义可知

令则有

因为L＜1，那么Φ为H2（［0，T］，Rm）×K上的压缩映像.由压缩映像原理可知，存在唯一的函数对（xt，μt）∈H2（［0，T］，Rm）×K满足系统（5）.证毕.

3 参随机微分变分不等式适定解的稳定性

下面将考虑含参随机微分变分不等式适定解的稳定性.

假定｛fα，gα，ψα，∀α∈A｝和ξα∈Rm为下述的含参随机微分变分不等式的函数族和随机变量族

其中KαRn中的闭凸子集族.

现给出将要用到的假设.满足ψα（·，·，x，μ）∈H2（［0，T］，Rn）和

其中c为正实数.

（B）函数族｛fα，gα，ψα，∀α∈A｝满足Lipschitz条件，其中Lipschitz系数为定义在假设1.5中的实数c1.

上关于α连续.

（D）ξα是f0-可测的，且在L2（P）上关于α连续.

注3.1由假设（A），可以定义H2（［0，T］，Rm）中的闭凸子集族Kα，并定义函数族Ψα如下：

（E）对于任意的α∈A，Ψα是强单调的，即存在实数c2＞0满足Rm）×H2（［0，T］，Rn），

注3.2由上述假设可知，系统（6）可以另行描述为

由上述假设，易见下述引理成立.

引理3.3系统（7）的解当且仅当下述映射的不动点Φα：H2（［0，T］，Rm）×K→H2（［0，T］，Rm）×K，其中Φα（x，μ）定义如下

引理3.4令L2＝max（（8T+T2+ρ2）c1+1-2ρc2，（8T+T2+ρ2）c1+2ρc2）＜1，其中c1、c2为假设1.3和假设1.5中的实数.如果（A）-（E）成立，则对于任意的

证明因为和Kα是闭凸集，那么也是闭凸集.可以用定理2.2类似的方法证明，所以在这里省略证明过程.

由引理3.4和Banach不动点定理，下面的引理显然成立.

引理3.5对于任意的α∈A，函数有唯一的不动点

由上述引理和假设，可以得到如下的主要定理.连续.

证明对于任意的α∈A，有

另一方面，

由定理的假设可知，如果ρ足够的小，那么

证毕.

致谢中国博士后基金项目（2018M643434）和中央高校基本科研项目（2015NZYQN70）对本文给予了资助，谨致谢意.