水介质耦合爆破中爆炸能量的传输特性研究

孙 颖，李 桐，陈 明，叶志伟

(武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072)

钻爆法是水利水电工程中常用的岩石开挖方法，然而自从炸药用于工程爆破以来，炸药爆炸的能量有效利用率一直维持在一个较低的水平，且在实际工程爆破中，由于降雨、淋水、水下爆破等原因，不可避免的要在炮孔含水的情况下进行爆破。工程实践和研究表明[1-2]，与传统爆破方式相比，水介质耦合爆破能够有效地控制空气冲击波，减少爆破飞石和产生有毒气体的数量，能降低爆破粉尘，较传统爆破方式而言具有显著的优越性。因此，深入研究水介质耦合爆破的能量传输特性，对了解含水炮孔爆破破岩机理，提高含水炮孔爆破工程的炸药能量利用率具有重要意义和工程实用价值。

理论和生产实践均证明[3-4]，炸药爆轰后的能量以两种方式传递给岩体，一种为冲击波能，一种为爆生气体膨胀能，前者主要消耗于爆腔的初始扩张，形成粉碎区和裂隙区以及岩石弹性变形上，后者则主要用于扩大爆腔，延伸裂隙和抛掷岩石。炸药能量通过爆炸后产生的爆轰波和爆轰产物撞击耦合介质传递到周围岩体中，传递至岩体中能量的多少与炸药性能、岩体性质和装药结构有关，为提升炸药能量利用率，对于传统的全耦合装药和空气耦合装药，众多科技工作者就炸药与矿岩的匹配展开了广泛的理论研究，并提出了波阻抗匹配[5-6]、全过程匹配[7]和能量匹配[8]等观点。当采用水介质耦合装药时，由于水介质的物理特性和动力学特性与空气介质不同，其爆破作用效果和传至岩体能量的多少也与传统空气介质耦合装药有显著不同，陈世海等[9]从理论上对水介质耦合装药爆破与炸药耦合装药的破岩效能进行了讨论，认为水介质耦合装药爆破能大大提高炸药的能量利用率；宗琦等[10]推导了水介质耦合条件下的孔壁峰值压力和破岩范围，认为炮孔水介质耦合装药比空气介质耦合装药更能提高爆炸能量利用率，增强破岩能力。

综上，目前关于水介质耦合爆破能量传递特性的研究还较少，主要停留在试验和定性分析阶段，本文采用理论和数值模拟相结合的方法，研究了水介质耦合装药条件下传递至岩体的爆炸冲击能量，并与同种装药条件下的空气介质耦合装药进行了对比。

1 水的动力学特性

与空气不同，在一千个大气压条件下，水介质密度变化很小，Δρ/ρ≈5%，在压力不大时可使用声学近似，但当炸药在水中爆炸时，爆炸瞬间释放大量能量，在装药本身体积内形成了高温、高压爆轰产物，爆轰产物膨胀压缩水介质，并在水介质中产生冲击波，此时，水具有一定的压缩性。

炸药爆炸在水中产生的冲击波满足连续方程、运动方程和能量方程：

ρ0(D-u0)=ρ(D-u)

(1)

P-P0=ρ0(D-u0)(u-u0)

(2)

(3)

式中：D为水中冲击波阵面速度；P0、ρ0、E0、u0分别为未经扰动水介质的压力、密度、内能和质点速度；P、ρ、E、u为水中冲击波波阵面通过后瞬间的压力、密度、内能和质点速度。

水中冲击波通过后熵值变化很小，近似地视为等熵过程，水的状态方程可写为[11]：

(4)

式中：n和A均为常数，Ф.А鲍姆根据实验给出的值为n=8，B=394 MPa。

2 水耦合炮孔能量传输过程

2.1 孔壁初始应力场

2.1.1 水耦合孔壁初始应力场

(5)

当冲击波传播至炮孔孔壁时，其峰值压力为：

(6)

(7)

其中，u(t)为t时刻的孔壁位移：

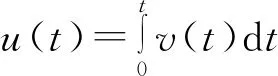
(8)

式中：v(t)为孔壁质点速度；t为时间。

将(7)式代入(4)式可得孔壁处水介质密度为：

(9)

联立(9)、连续方程(1)和运动方程(2)，假设水介质初始时处于静止并忽略静水压力，可得孔壁处水中冲击波波速D1为：

(10)

按声学近似原理，可求解孔壁冲击波初始压力[4]：

(11)

式中：ρm孔壁岩石的原始密度；Cp为岩体中的纵波波速。

将孔壁处冲击波入射压力P1代入上式有：

(12)

依据动量守恒有：

Pt=ρmCpv(t)

(13)

结合式(8)、(12)、(13)便可得到水介质耦合时孔壁v(t)、u(t)和Pt随时间的变化规律。

2.1.2 空气耦和孔壁初始应力场

对于空气耦合，假设爆生气体膨胀过程分为等熵膨胀和绝热膨胀两个过程，当不耦合系数较小时，爆炸压力大于炸药临界压力Pk，按等熵膨胀计算，孔壁初始冲击压力：

(14)

当不耦合系数较大时，对于爆炸压力小于临界压力阶段，按绝热膨胀计算，孔壁峰值压力可按下式计算：

(15)

式中：Pb为孔壁峰值压力；k、v为绝热指数，通常取k=3，v=1.3；D为炸药爆速；n为压力增大倍数，与炸药特性、不耦合系数、岩体介质相关，并不是一个常值[12]；Pk为临界压力，一般中等威力炸药，Pk=200 MPa；Pe为平均爆轰压力，其值为：

(16)

因此，结合式(8)、(13)、(14)、(15)就可求得空气耦合时孔壁v(t)、u(t)和Pt随时间的变化规律。

2.2 炮孔壁能量传递过程

炸药能量通过爆炸后产生的爆轰波和爆轰产物撞击耦合介质传递到周围岩体中。炸药爆炸后，爆源向周围介质释放出的能量只是引起爆炸产物及其周围介质运动的炸药化学能的一部分。转移到距爆源一定距离的岩体中的能量是衡量有用功的标准，在冲击波通过后，通过孔壁单位面积传至岩体的能量可按下式计算[4]：

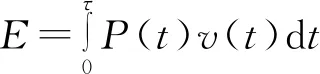
(17)

式中：v(t)为孔壁质点速度随时间变化的函数；τ为压缩作用时间。

将爆轰波或爆轰产物与孔壁的碰撞简化为弹性碰撞，E可以写为：

(18)

因此，依据前述求得的水介质和空气耦合条件下的孔壁质点速度，便可得到应力波通过后传至岩体的能量随时间的变化规律。

2.3 算例分析

为进一步研究近似弹性状态下的爆炸能量传递特性与周围岩体介质、不耦合系数和耦合介质的关系，选择花岗岩和砂岩分别代表硬岩和软岩两种岩体介质, 选用装药直径和炮孔直径比分别为50/90、40/90、32/90的3种装药结构，选用乳化炸药(密度ρe=1 300 kg/m3，爆速D=4 000 m/s，爆热QVS=3 760 kJ/kg)展开研究。岩体的具体物理力学参数如表1所示。

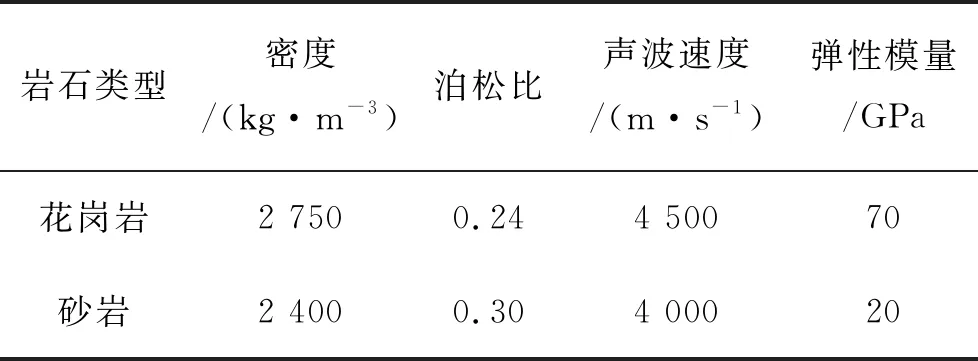
表1 岩体物理力学参数表

代入理论计算公式可得各装药条件下的孔壁峰值压力如表2所示。

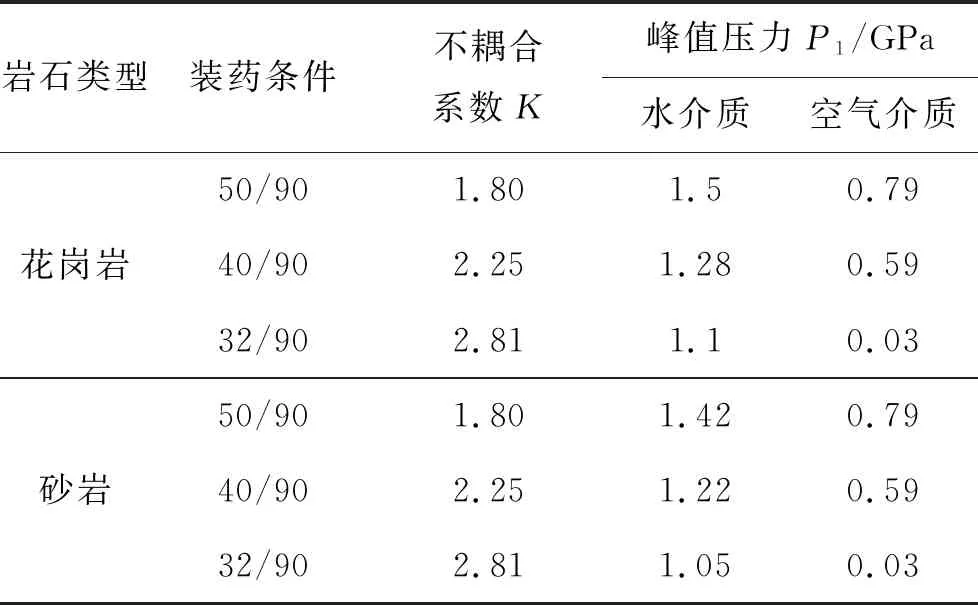
表2 孔壁峰值压力理论结果表

依据理论计算得到不同岩体介质条件下的孔壁压力和能量随时间的变化规律一致。以花岗岩(硬岩)为例，不同耦合介质和不耦合系数条件下，其孔壁压力和能量随时间变化的曲线如图1、2所示。

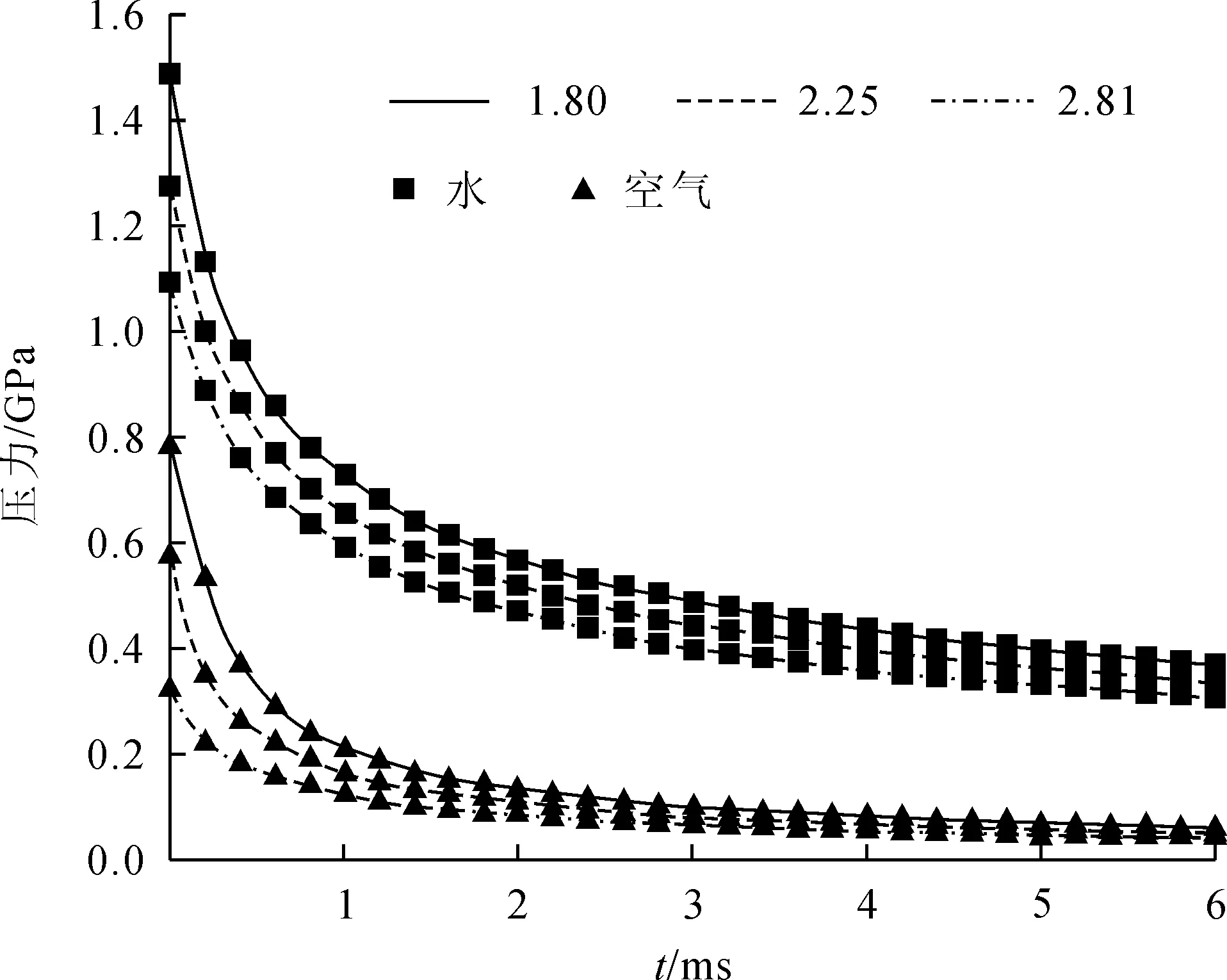
图1 孔壁压力时程曲线图

图2 孔壁能量时程曲线图

由图1可知水介质耦合和空气介质耦合条件下，炮孔孔壁压力随时间衰减规律相同，呈初始时迅速下降而后逐渐平缓的规律，但水介质耦合条件下其峰值压力下降速度较慢，此外，水介质耦合条件下的孔壁初始峰值压力较空气介质耦合条件大；由图2可知，两种耦合介质条件下，传至孔壁能量随时间变化规律相同，随着冲击作用时间的增加，孔壁能量逐渐增大，因此，冲击作用时间对能量传递有较大影响，只要确定各装药条件下的冲击作用时间，便可得到传至岩体能量的理论解。当岩体介质为砂岩(软岩)时的孔壁压力和能量的变化规律与硬岩类似，由表2可以看出，岩体介质性质对峰值压力也有影响，对水介质耦合装药来说，传至硬岩的压力较软岩大。

3 水耦合爆破能量传递数值模拟

由于炸药爆炸过程中伴随着各种参数随时间和空间的急剧变化，往往对其进行一系列的假设和简化才能得到一些问题的解析解，因此，本文采用了数值模拟的方法对水介质和空气介质耦合条件下的能量传递特性进行了研究，进一步验证理论推导结果的合理性。

3.1 计算模型及参数

数值计算中采用Autodyn的流固耦合算法模拟炸药的冲击作用，其中，岩体采用线弹性材料进行模拟并采用Lagrange算法；炸药、水、堵塞采用Eulerian算法，能实现材料在网格中流动，有效计算爆炸冲击过程中的大变形问题。

模型具有对称性，为节约计算时间，采用1/4模型，尺寸为3.0 m×3.0 m×1 m，采用90 mm炮孔，药卷直径分别采用50 mm、40 mm和32 mm，其余部填充水介质或空气介质。为能模拟出真实的爆炸效果，模型炸药和水单元的尺寸控制在3 mm以内，炮孔近处岩石单元尺寸也和炸药、水介质单元尺寸相近。所建立的模型的单元数量约为25万，节点数量约为27万。同时计算的时间步也要和模型最小单元尺寸相匹配，以便观察到冲击波与孔壁的透反射效果。在计算模型的对称边界施加对称边界，其余面施加无反射边界，如图3所示。

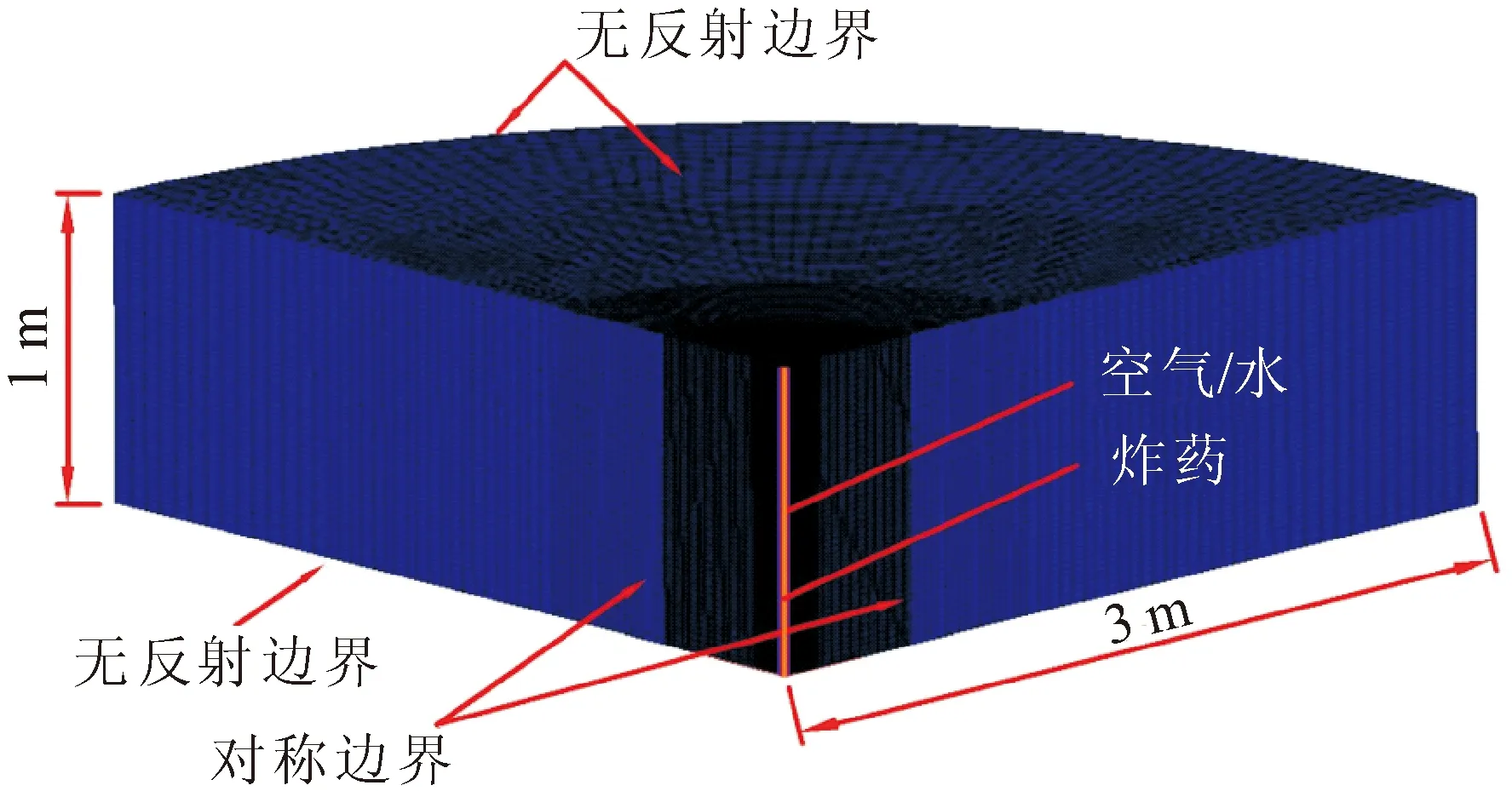
图3 计算模型示意图

炸药采用JWL状态方程进行模拟，其爆炸过程中的压力和内能及相对体积之间的关系：

p=A1(1-ω/R1V)e-R1V+B1(1-ω/R2V)e-R2V+ωE0/V

(19)

式中：p为爆轰压力；V为爆轰产物的相对体积(爆轰产物体积和炸药初始体积之比)，相关参数取值见表3。

表3 炸药相关参数表

岩体采用线弹性材料，对于花岗岩，其密度ρ=2 750 kg/m3，体积模量A=44.8 GPa；对于砂岩，其密度ρ=2 400 kg/m3，体积模量A=16.7 GPa。

水介质采用Polynomial状态方程进行模拟，当水压缩时(μ>0)，状态方程为：

(20)

式中：P为水中压力；μ为压缩比μ=(ρ/ρ0-1)；e为水的内能；ρ0为水密度，取为1 g/cm3；A1=T1=2.2×106kPa，A2=9.54×106kPa，A3=1.46×106kPa，B0=B1=0.28，T2=0。

空气采用Ideal Gas状态方程

P=(ζ-1)ρe

(21)

式中：ρ为空气密度，取1.225 kg/m3；e为空气初始内能；ζ为材料常数，取1.4。

3.2 模拟结果分析

图4、5、6绘制了周围岩体为花岗岩，不耦合系数为1.80时的孔壁压力、孔壁位移和传至孔壁能量的时程曲线。从图4可以看出，水介质耦合条件下传至孔壁峰值压力显著大于空气介质耦合时的孔壁峰值压力，与计算分析的结果基本一致，且水介质耦合条件下的准静态压力较空气介质耦合高；从图5可知，水介质耦合条件下，孔壁质点位移明显大于空气介质耦合条件；由图6可知，两种耦合介质条件下传至孔壁的能量随时间的变化规律与理论分析结果一致，随着时间的增大，传至孔壁能量逐渐增大，并趋于一定值。其余装药条件下的数值模拟结果和上述结果规律一致。

考虑到准静态压力作用对孔壁质点位移贡献较小，将孔壁质点位移达到峰值时的时间作为冲击作用时间，依据算例计算得到的孔壁能量时程曲线，便可得到传至孔壁能量的理论解。表4给出了数值模拟得到的不同条件下，孔壁峰值压力和位移，并给出了位移达到峰值的时间。依据表中的数据和理论计算的能量时程曲线，得到的传至岩体能量的理论和与数值模拟结果的比较如表5所示。

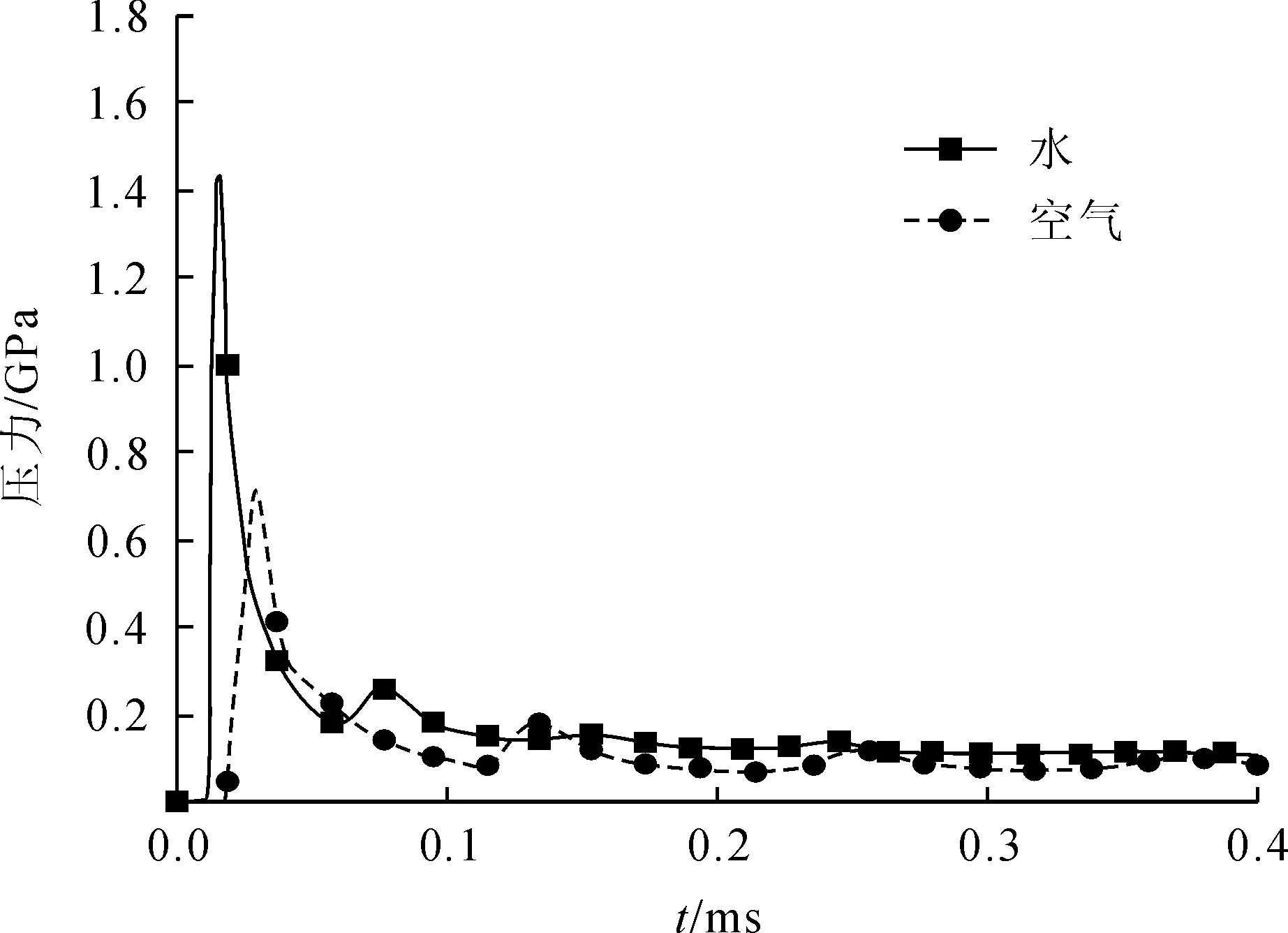
图4 数值模拟孔壁压力时程曲线图

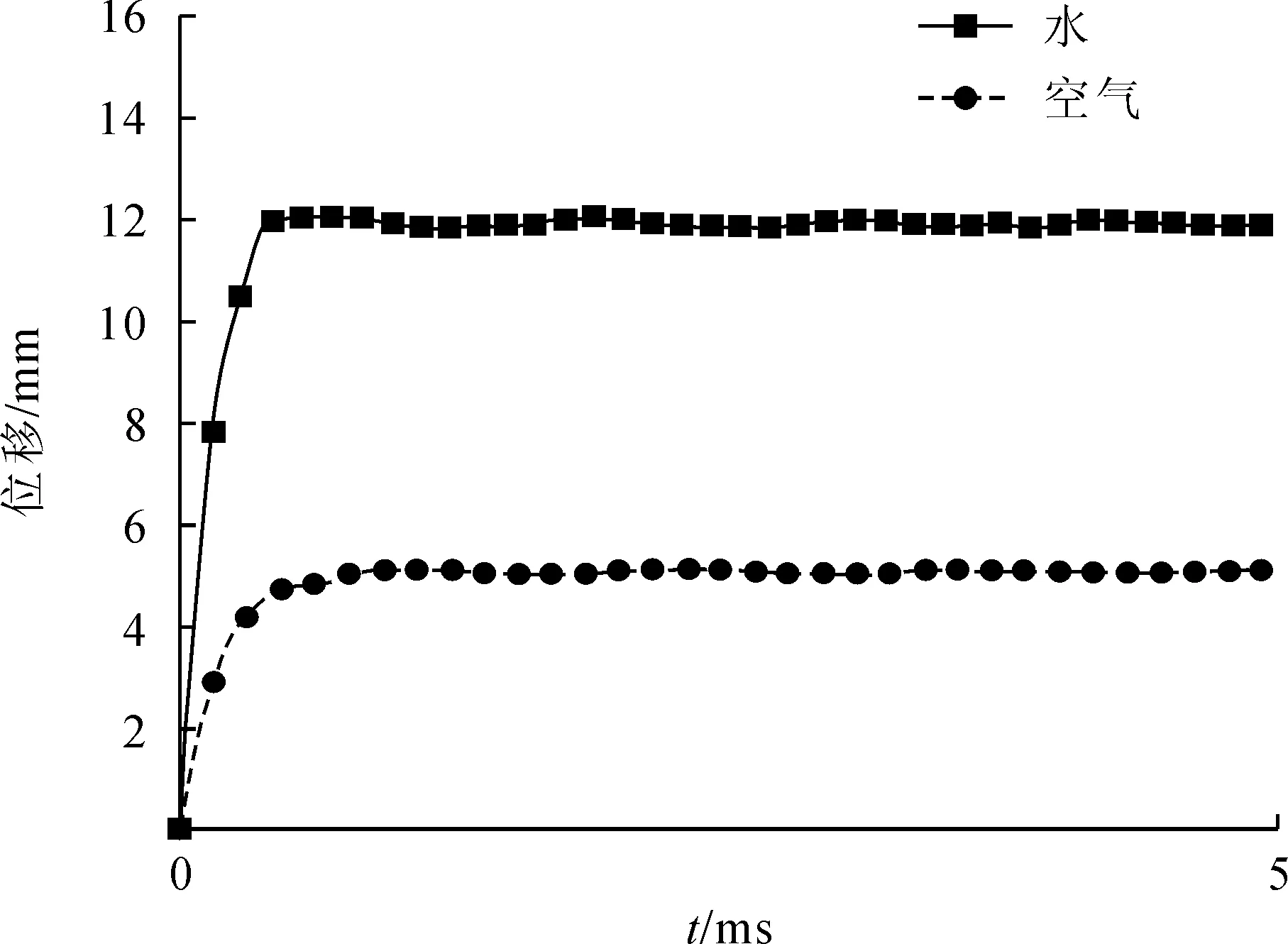
图5 数值模拟孔壁位移时程曲线图

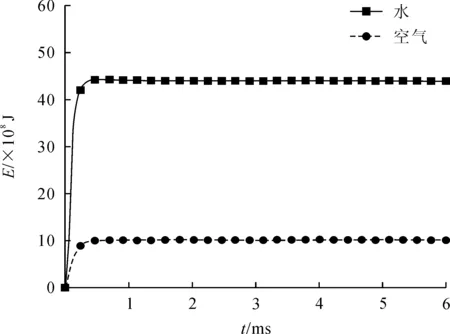
图6 数值模拟能量时程曲线图

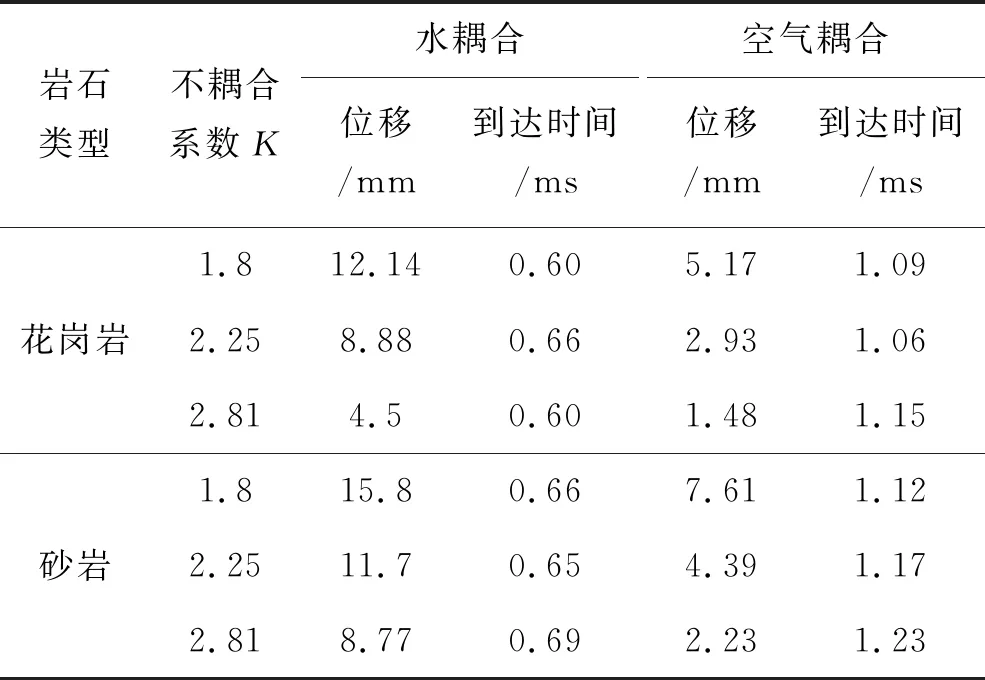
表4 两种耦合介质条件下的孔壁峰值压力与位移表

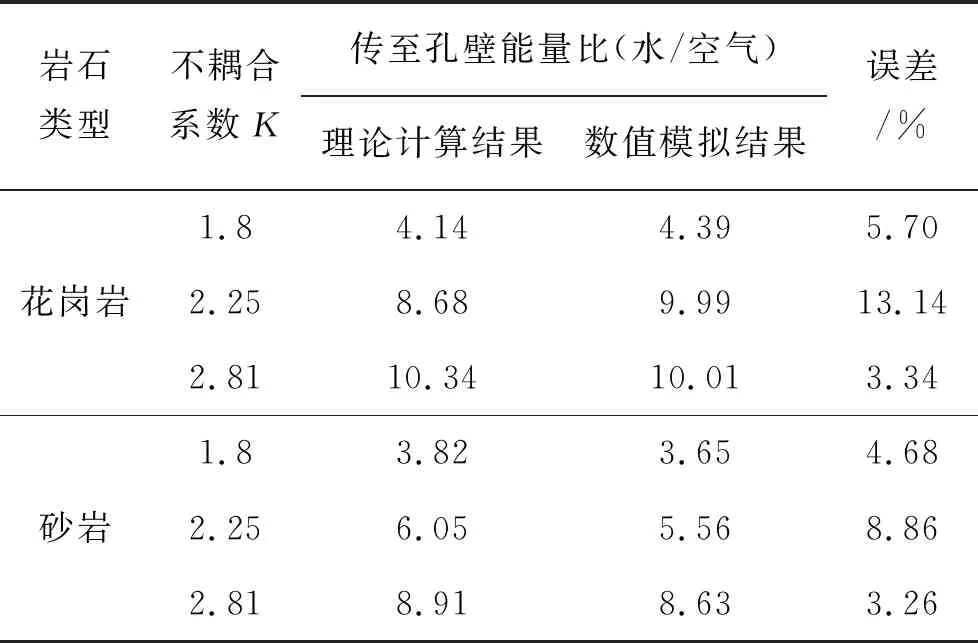
表5 传至周围岩体能量关系理论解表

由表5可知，依据算例计算得到传至孔壁能量的计算结果与数值模拟结果规律一致，随着装药不耦合系数的增大，装药量一致时，采用水介质耦合装药时提升炸药能量利用率效果明显，且硬岩的提升效果更为显著。根据理论计算结果，随着不耦合系数的增大，经由两种耦合介质传至岩体的能量差异增大，当不耦合系数由1.80增至2.81时，对于花岗岩，采用水介质耦合装药传至周围岩体的能量由空气介质耦合装药的4.14倍增至10.34倍，对砂岩来说，采用水介质耦合装药传至周围岩体的能量由空气介质耦合装药的3.82倍增至8.91倍。依据表5中的对比分析结果，对于传至孔壁的能量，理论计算结果和数值模拟结果的误差保持在15%以内，因此，此理论计算方法能较好的描述水介质耦合爆破时的能量传递过程。

4 结 语

1)炸药爆炸后，爆轰波和爆轰产物经过耦合介质后作用于周围岩体，水介质由于其较高的密度、较大的流动粘度和较低可压缩性，使爆轰波穿过后作用于岩体的峰值压力较空气耦合时大，增强了炸药破岩能力。

2)装药结构相同时，相对空气介质耦合而言，水介质耦合能提高准静态压力，减少了爆生气体膨胀过程中能量的耗散，更有利于准静态阶段的驱裂，提高了炸药能量利用率。

3)理论分析和数值模拟相结合，研究了炸药-水/空气介质-周围岩体这一能量传输过程，较好的确定了水介质和空气介质耦合条件下岩体的孔壁峰值压力和传至岩体的能量传输特性。结果表明，装药结构相同时，水介质耦合装药传至岩体的能量比空气介质耦合装药高，且岩体为硬岩时能量效率差别更大；随着不耦合系数的增大，经由两种耦合介质传至岩体的能量差异增大，当不耦合系数由1.80增至2.81时，对于花岗岩，采用水介质耦合装药传至周围岩体的能量由空气介质耦合装药的4.14倍增至10.34倍，对砂岩来说，采用水介质耦合装药传至周围岩体的能量由空气介质耦合装药的3.82倍增至8.91倍。