水电集群调控分解协调关键耦合因子研究

何 滔，汪广明，汪文元，熊 玺

(国家能源大渡河沙坪发电有限公司，四川 乐山 614300)

充足的调峰能力和快速的响应能力是保持电网稳定对电力系统电源端提出的十分重要的要求之一。梯级水电短期内分级调能效果受到水库耦合性、水流时滞性、机组爬坡率、水文气象、电站调度等多种原因的影响，是一类典型的大规模、强耦合、多约束、动态、离散的复杂非线性优化问题,也是水电能源优化运行领域的研究热点之一[1-6]。在梯级水电联合调度过程中，往往易忽略控制性龙头水库的负荷波动情况，而下游电站的不规律调节和被动跟随与其相关性显著。采用斯皮尔曼系数的加权朴素贝叶斯算法定量描述条件属性与决策类之间的相关性，从而为目标电站分解协调算法调控中各条件属性赋予相应权值，部分消除了耦合条件独立假设对影响因子分类效果的影响。

1 水电站的不规律调节及其影响因子关联性分析方法

采用斯皮尔曼系数的加权朴素贝叶斯分类算法来确定电站不规律调节与各影响因子之间的关联性及关联强度。其分类式可表达为：

式中：Cj为电站不规律调节影响因子数据集中m个类，j=1,2,3,…,m；P(Cj)表示Cj类发生的先验概率；wk为电站负荷区间、流量变化区间、库区水位变化区间等条件属性与上游电站负荷波动耦合、站内条件要求、自身库容约束、控制水位要求、调度要求等决策类之间的斯皮尔曼系数ρk的权值。

2 水电集群联合调能的必要性

大渡河流域上游往下游选取邻近几个梯级电站：瀑布沟、深溪沟、枕头坝、沙南、龚嘴、铜街子，其中电站瀑布沟、深溪沟、枕头坝已经实现了三站联调且瀑布沟是下游几个电站的控制性水库，龚嘴、铜街子也已实现了两站联调，而沙南电站由于2019年5月进入全投，机组尚未经历完整检修期的设备稳定性检验，设备定值、缺陷也尚需调整和治理，水库调度规律仍需在实际投产发电的完整周期年中完善探索，因此沙南电站尚未纳入联调队列。在各种因素的影响下，未纳入集群调能电站局限性表现的相对明显，具体表现如表1所示。

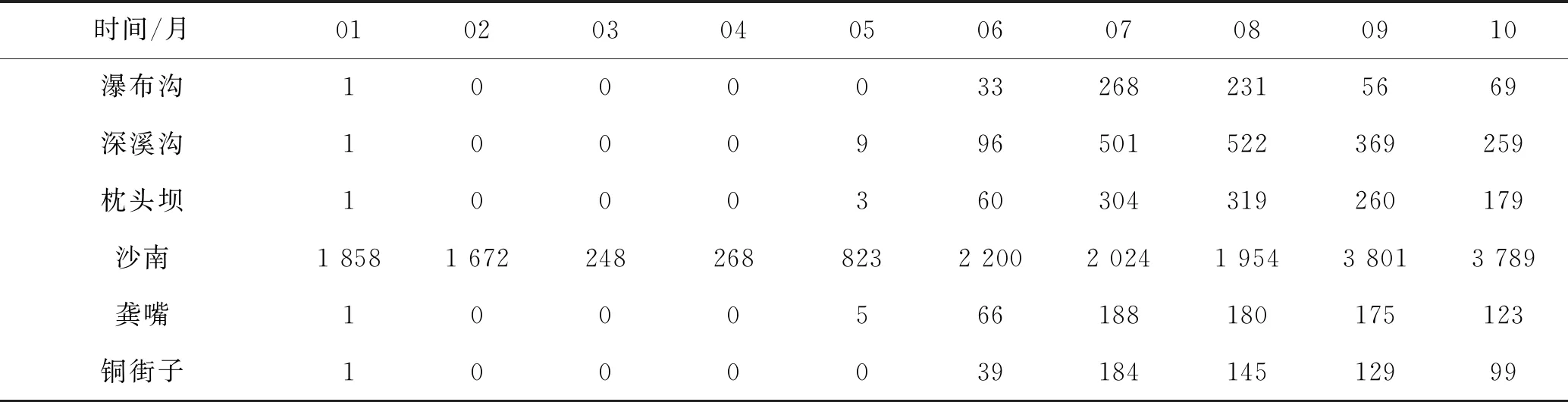
表1 大渡河流域梯级电站对应月泄流设施动作统计表

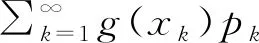
3 水电集群调能关键耦合因素分析

水电站控制的主要战略对象是发电量与水资源，其控制主要是调节发电量与水资源的耦合动态平衡关系。而影响此类耦合动态平衡关系的几个主要影响因素有：电站的固有属性、耦合电站负荷波动、计划负荷与实时发电之间关系、自身内部控制等。

3.1 电站固有属性分析

选取流域几个邻近电站进行固有属性分析，如表2所示。

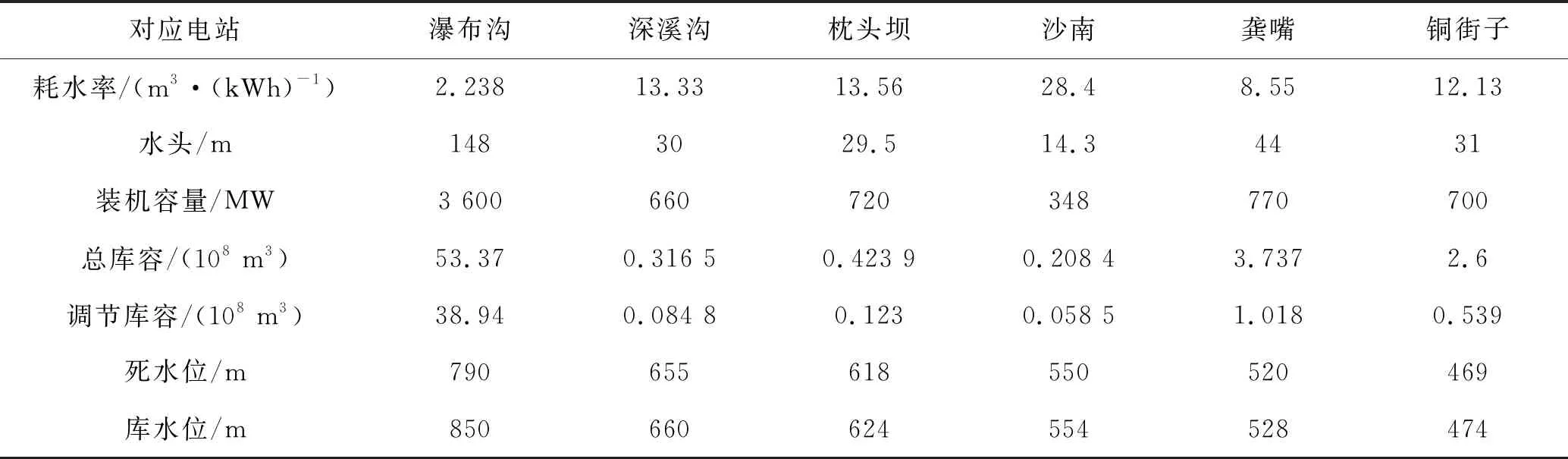
表2 大渡河流域梯级电站固有属性表

从固有属性可知，沙南电站在集群电站中具有最大耗水率、最小可调节库容两大典型特征，电站自身库容小影响了其调节能力。选择与沙南电站库容相近的深溪沟，深溪沟调节库容(848万m3)约为沙南的1.44倍，单从调节时间裕度来说，深溪沟、沙南两站差别不大，但从最终泄流设施动作情况来看，深溪沟明显少于沙南同期。

在研究对象样本容量中随机抽样选取连续时间段瀑布沟、深溪沟、枕头坝、沙南四站有功数据进行联合分析，得出集群调能电站瀑布沟、深溪沟、枕头坝三站全站实时出力曲线跟随性较好，三站负荷变化频率、步调基本一致，三站期间泄流设施动作总次数0次，充分体现了水电集群联合调能的优越性；期间沙南负荷波动量较少，波动幅度与波动频率低，闸门动作次数21次，负荷调节更多是“跟趋势”，步调难与上游电站保持一致。由于沙南电站现阶段仅能依靠人工观测上游三站负荷增减情况来向调度中心申请负荷，导致负荷难与上游三站步调一致，最终上游库水位的控制主要依靠泄流设施进行控制。因此调节库容小不是泄流设施动作频繁的最主要影响因素。

3.2 电站负荷波动耦合关系分析

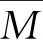
为尽量减少沙南电站闸门动作次数，降低闸门动作频率，认为沙南电站闸门每次必要动作为1 m，则对应期望流量变化范围在198.11～216.05 m3/s。为便于计算，取变化流量为200 m3/s。

经统计，选择2018年1月至10月瀑布沟、深溪沟、枕头坝三站对应整点负荷及沙南泄流设施动作为样本进行分析，可以发现沙南临近上游三站在此时段中负荷波动情况及波动概率较大，如表3所示。

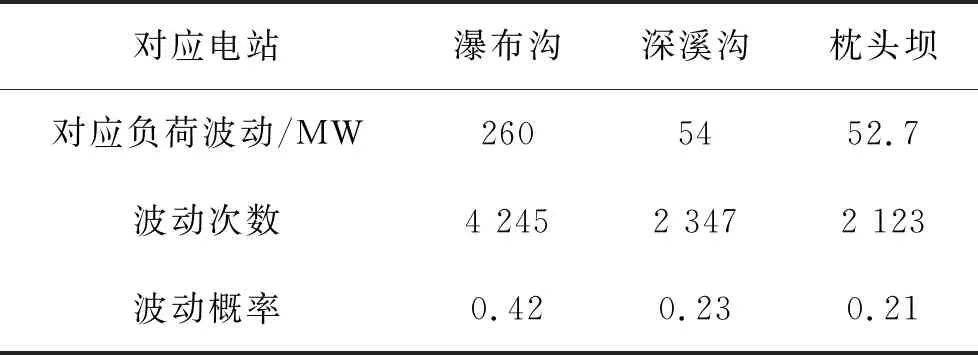
表3 沙南电站上游三电站对应负荷波动及波动频率表

从负荷波动及其频率中可以看出，上游三站负荷平均波动概率为0.286 7，总波动概率为0.284 7，偏差为0.002，在95%置信区间范围内。

分析上游三站与沙南电站泄流设施动作相关性，记沙南泄流设施分为动作与不动作两种情况。泄流设施动作大于或等于1均记为1，所有泄流设施均不动作记为0。考虑到水流时间滞后性，分别取瀑布沟、深溪沟、枕头坝、沙南(记为A、B、C、D)响应时间间隔ΔtA,D、ΔtB,D、ΔtC,D为4、3、2 h，若上游对应电站负荷波动且沙南泄流设施动作则记为1，否则记0，以沙南上游三站负荷波动为自变量，沙南泄洪闸是否动作为因变量，构建基于斯皮尔曼系数的朴素贝叶斯分析模型，得到协同动作样本与协同动作概率，结果如表4所示。

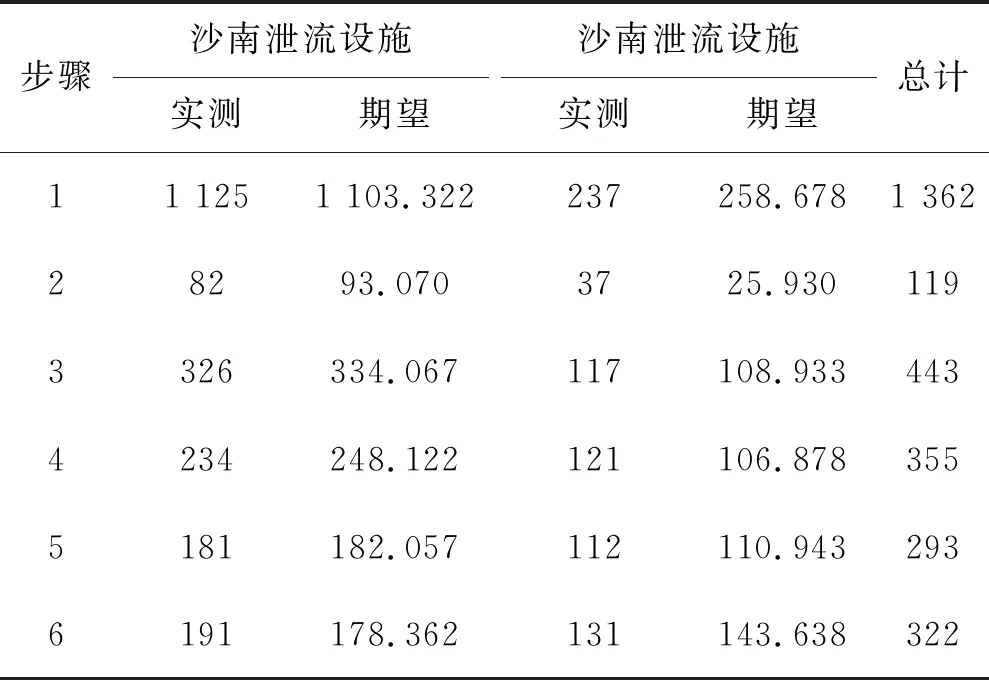
表4 沙南电站泄流设施动作霍斯默-莱梅肖检验列联表 次

基于斯皮尔曼系数的加权朴素贝叶斯算法可定量描述条件属性与决策类之间的相关性，消除条件独立假设对耦合关联效果的影响。它是衡量变量间的依赖性的非参数指标，利用单调方程评价统计变量间的相关性[7-9]。

对该模型进行拟合优度检验，检验预测值和实际值之间差别的大小，进行多次数据拟合试验，以判断得出结论的可靠性。H-L检验的随机性表是比较观测值与期望值，经观测，表中期望值与实测值误差极小，表明该模型拟合度较高[10-12]。

通过以上数据分析，发现控制性瀑布沟负荷波动对未纳入集群联合调能队列的沙南泄流设施动作总次数有决定性影响，沙南泄流设施动作与紧邻上游电站枕头坝负荷波动规律跟随性更好，枕头坝负荷波动在短时间内可能很大程度直接影响沙南泄流设施动作情况，但在长期规律来看沙南泄流设施动作总次数更大程度受制于瀑布沟负荷波动。如图1所示。

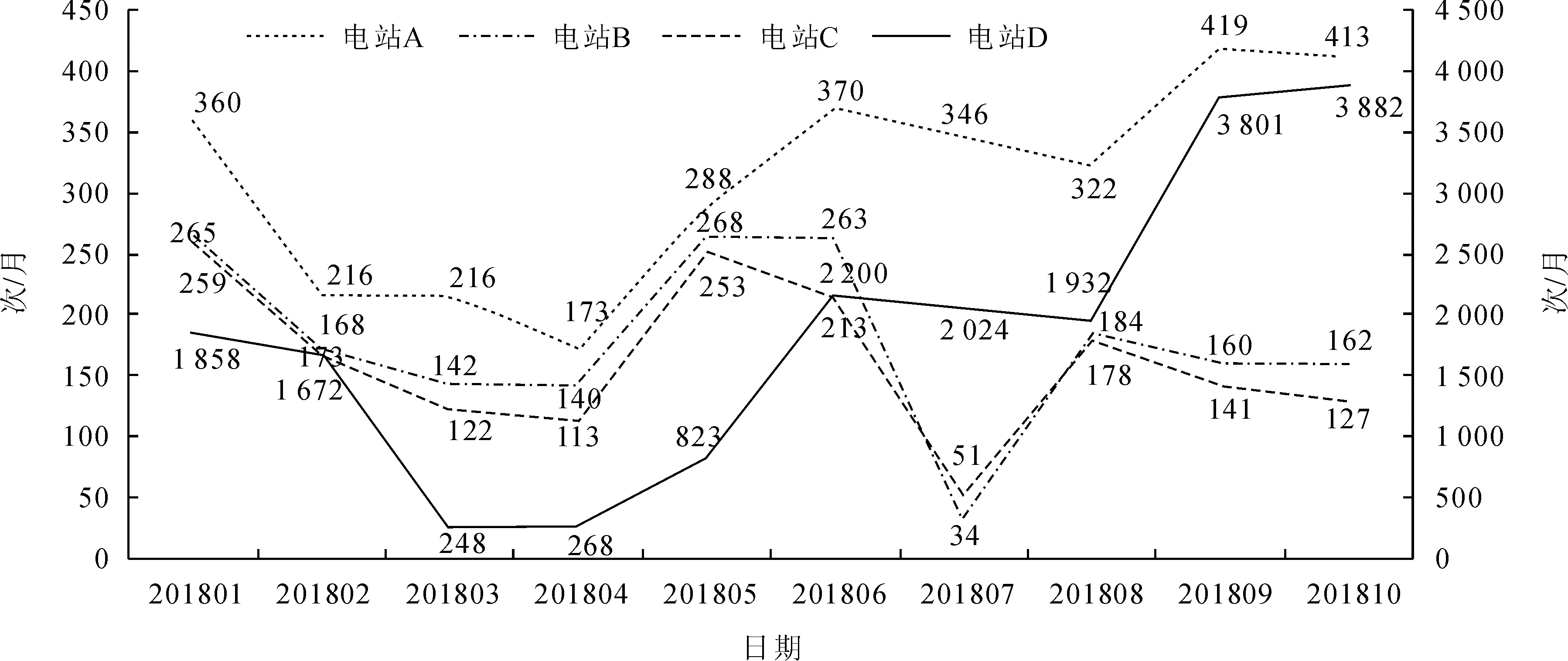
图1 沙南上游三电站负荷波动与沙南闸门动作表征图

斯皮尔曼相关系数表明X(独立变量)和Y(依赖变量)的相关方向。如果当X增加时，Y趋向于增加，斯皮尔曼相关系数则为正。如果当X增加时，Y趋向于减少，斯皮尔曼相关系数则为负[13-14]。斯皮尔曼相关系数为0表明当X增加时Y没有任何趋向性。当X和Y越来越接近完全的单调相关时，斯皮尔曼相关系数会在绝对值上增加。当X和Y完全单调相关时，斯皮尔曼相关系数的绝对值为1[15]。

对沙南泄流设施动作次数与上游三站负荷波动频率进行斯皮尔曼系数的加权朴素贝叶斯算法检验并做相关性分析，结果如表5所示。

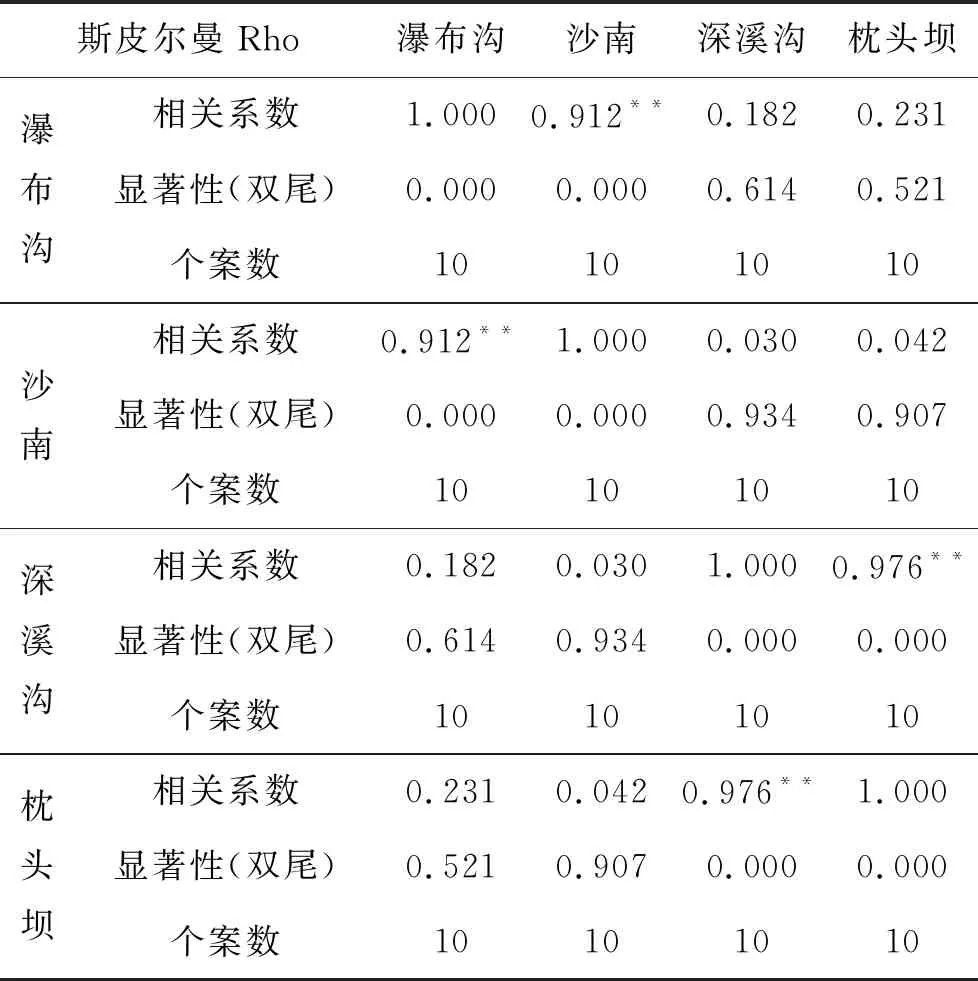
表5 四个电站斯皮尔曼相关系数及显著性表

通过相关性可看出，从总量角度来看，瀑布沟负荷波动与沙南泄流设施动作相关系数为0.912，深溪沟负荷波动与沙南泄流设施动作相关系数为0.03，枕头坝负荷波动与沙南泄流设施动作相关系数为0.042。

以上结果可以印证未纳入集群联调队列电站泄流设施动作频率极大相关于上游控制性水库泄流，周期响应频率相关于上游最邻近电站泄流量的结论。

3.3 考虑上游控制性水库负荷波动频率耦合因子的水电集群分解协调调控

水电集群调控分解协调思想是将水电集群大系统暂时割裂为若干独立子系统，并在系统分解层逐步分别寻求局部最优解；在各子系统最优解或已有解的基础上，恢复各子系统之间耦合关系，并在系统协调层通过耦合变量进行更高级协调，达到全系统最优。

模型以优化调度模型为切入点，考虑到子系统内瀑布沟、深溪沟、枕头坝、沙南之间的联系与制约，分解层分别考虑四站的负荷调整时间与调整量、泄流设施调整时间与调整量及四站机组和泄流设施的运行状态，系统协调层则考虑到发电量最大、泄流设施动作最小及水位约束、生态流量约束、机组避开振动区的目标，应用目标协调法构建Lagrange函数，将水量平衡约束和各站间流量耦合约束纳入协调目标。

整个过程中，充分考虑上游控制性水库电站(分析模型中的瀑布沟电站)负荷波动频率耦合因子，与原仅关注上游物理位置临近电站负荷变化(分析模型中的枕头坝电站)的调度方案对比，沙南电站年发电量可增加1.385亿kW·h，减少弃水量34.348亿m3，泄流设施动作次数减少62.21%，水库耦合补偿效益显著。

4 结 语

1)控制性水库下游未纳入流域统调的电站负荷及水调跟随性较差，丰水期导致自身泄流设施频繁动作，增加泄流设施及下游防汛潜在安全隐患。

2)在实际调控过程中，充分考虑上游控制性水库电站负荷波动频幅，能一定程度上提升大渡河流域瀑布沟以下水电集群安全稳定性与沙南电站负荷承担能力，可对其它流域水电调控提供一定的参考。