多层分子污染膜光学效应建模分析与试验测量

2021-03-15杨生胜

航天器环境工程 2021年1期

乔佳，杨生胜，王鹢，郭兴

（兰州空间技术物理研究所，兰州730000）

0 引言

航天器上的非金属材料在真空和高温下会产生出气分子，并扩散沉积到敏感表面。若沉积到太阳电池表面将导致电池输出功率下降；若沉积到光学表面将影响光学器件的透射率和反射率。

关于分子污染对光学器件的影响，国外学者做了大量研究工作。有研究表明，被氢离子处理过的铝沉积氧化锌（AZO）薄膜内的氧空穴和O—H 键增加，使薄膜的透射率、折射率增大，消光系数在短波长范围内减小。在辐射深度对纳米晶体氧化薄膜影响的研究中发现，薄膜光学带宽随着辐射深度增加而增加。对用于太阳电池板异质结构NiOTiO薄膜光学性能的研究结果表明，在可见光范围内该薄膜的吸收率可达98%，在红外范围内吸收率下降到2%。以上研究均只给出了影响薄膜光学性能的因素，并未给出具体预估模型。Bertrand利用洛伦兹-洛伦茨关系研究了混合气体和纯净气体的折射率与消光系数的关系，由于对每种气体成分浓度以及碳氢键连接程度的测量存在误差，导致实验值与理论值存在偏差。2018年日本空间探测研究中心基于谐振模型HOM以及有效介质近似理论EMA研究环氧树脂出气污染膜对光学器件性能的影响，并比较污染膜厚度的理论计算值与实际测量值，以验证所建立的模型。但是该研究中建立模型的11个参数是通过对透射率测量值的拟合获得，而由文献[15]可知，其中介电常数在距离过渡面10 nm 范围内变化较大（在此范围外基本保持稳定），但该研究并未区分过渡面与非过渡面，从而导致计算值与实验值间存在误差。

国内学者在材料出气污染方面的主要研究关注点在光学器件污染防控措施以及粒子污染物对光学器件的影响，很少研究分子污染对光学器件的影响。本文在国内外现有研究的基础上开展多层膜分子污染光学效应模型的研究，思路是：基于薄膜在分层媒质中的传播和介质膜理论建立多层薄膜光学污染效应模型，并采用Goos-Male方法计算每层薄膜的光学常数和厚度，然后利用洛伦兹-洛伦茨关系并结合EMA 理论计算粗糙表面以及过渡面的光学常数，将所获得的污染薄膜光学常数和厚度代入多层薄膜光学污染效应模型中，计算研究污染膜的光谱透射率和总透射率。具体是以信号电缆屏蔽线PVC材料外部绝缘层和33+黑色绝缘胶带为污染源，沉积在光学玻璃表面，测量被污染光学玻璃在紫外、可见光和红外波段的透射率；并开展试验测量，将测量值与模型计算值进行比较，以验证模型的有效性。

1 模型建立

1.1 多层薄膜光学污染效应模型

试验过程中污染源正对着光学玻璃，因此沉积在光学玻璃上的污染层中心附近可近似为均匀沉积。材料中不同出气成分的沉积顺序不同，实际沉积污染膜是顺序累加的多层膜。本文主要研究2种非金属材料先后沉积所形成的多层膜，且在计算过程中考虑材料间的过渡层以及表面粗糙情况，建立多层污染膜光学效应模型（如图1所示）。

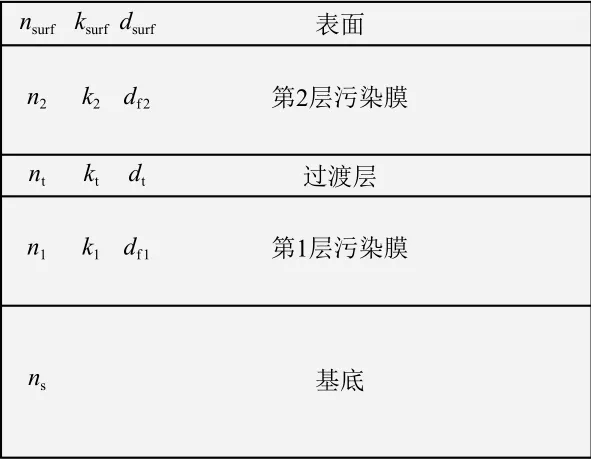
图1 多层污染膜光学效应模型Fig.1 Theoptical effect model of multi-contaminated films

多层污染膜光学效应模型的主要影响参数包括每层膜与过渡层的厚度d、折射率n和消光系数k以及层数等。在多层模型中，如果给出每个膜层的特征矩阵

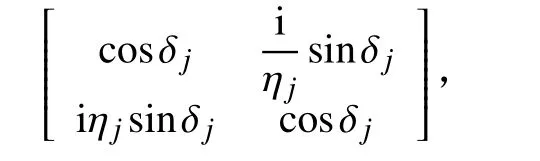
则可通过将各膜层特征矩阵相乘获得多层膜的特征矩阵

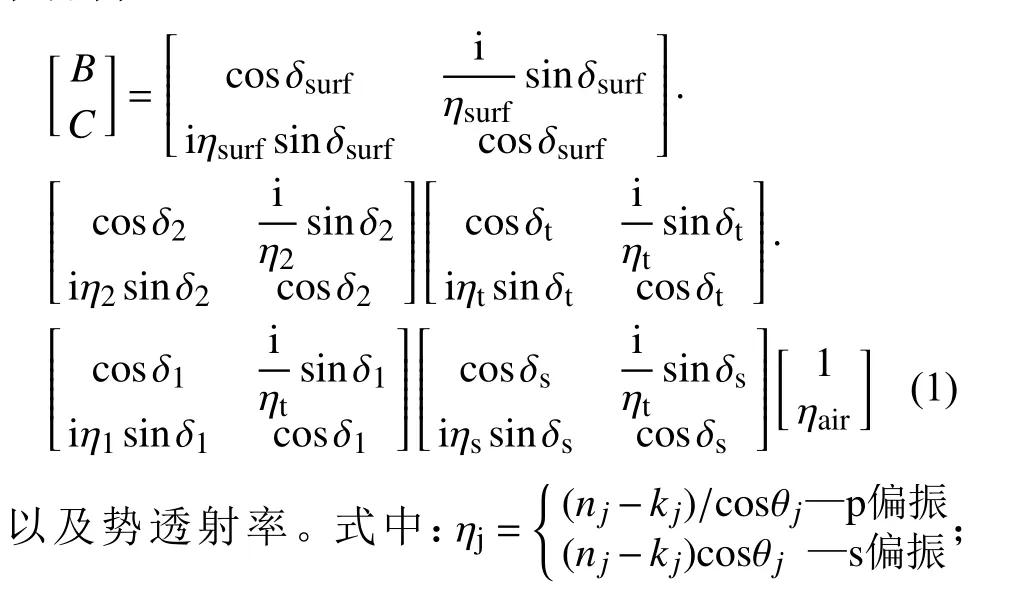
式中，η为空气导纳，*代表共轭。

由式(1)～式(3)可知，只需测量得到各层污染膜的厚度及其光学常数，结合入射角，就可计算得到多层膜的反射率和透射率。

1.2 光学常数获取方法

1.2.1 单层膜光学常数计算

本文采用Goos-Male 方法计算单层膜光学常数，原理如图2所示，采用波长为λ的S极化的光线以入射角θ入射样品表面，首先正面照射薄膜，测量反射光R和透射光T（其中下标代表层的顺序，a 为空气，f 为污染膜，s为基底），如图2(a)所示；然后光从背面照射基底，测量其反射光R和透射光T，如图2(b)所示。若测试设备正常，则应有T=T。最后代入相关表达式，计算得到薄膜光学常数和膜厚。

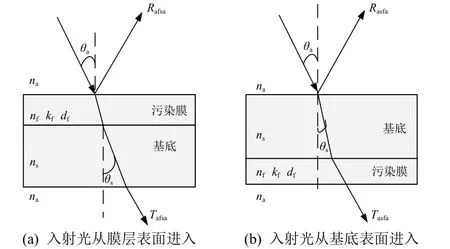
图2 单层膜光学常数计算原理Fig.2 Principle for calculating the optical constants of monolayer films

1.2.2 过渡层以及粗糙表面光学常数的计算

洛仑兹-洛伦茨公式可以将材料中每种成分的数密度N 与材料的光学常数关联起来（n′=n-ik）。对于单一材料，其光学常数n与其质量密度ρ之间的洛伦兹-洛伦茨关系为

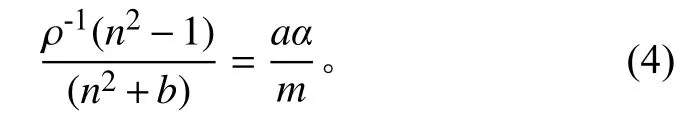
式中：ρ=mN，m为分子的平均质量；α为每个分子的平均极化度；a 和b为局部场参数。如果均匀介电常数只包含非极化分子，则a=(3ε)，b=2。

可以利用洛伦兹-洛伦茨关系，根据每种材料光学常数计算过渡层光学常数，并根据上层材料以及空气的光学常数计算粗糙表面光学常数。洛伦兹-洛伦茨关系的关键点是第j 种材料的光学常数n与第j 种材料的分子平均极化度相关，

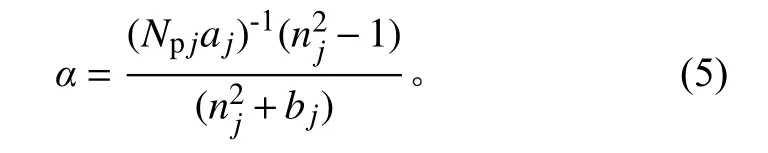
式中：N为纯净材料中第j 种成分的数密度；a和b为纯净材料合适的局部场参数，而且混合物的平均分子极化度α 为混合物中每种成分的极化度权重平均，

因此，混合物的光学常数为

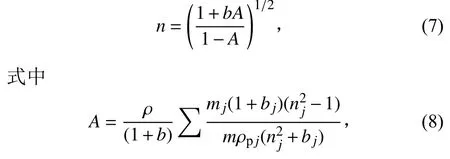
其中：ρ为混合物的质量密度；ρ为纯净物的质量密度；m为纯净物的平均分子质量。

取b=b=2，同时假设混合物只有2种材料，且每种材料近似为纯净物，则

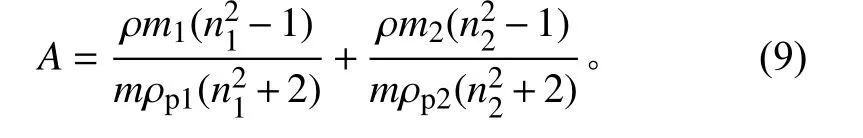
其中混合物及2种纯净材料的质量密度和分子质量均可通过测量获得。

综上，通过材料密度和分子质量的测量，结合式(9)和式(7)的计算，可获得粗糙表面以及过渡层的光学常数。

1.3 多层膜厚度计算

为了解决薄膜厚度数据误差带来的计算误差，本文提出一种计算多层污染膜实际厚度的方法。首先获得2种材料在制备单层污染膜时的出气量m、m和厚度d、d，以及制备多层污染膜时每种材料的出气量m′、m′和厚度d′、d′；考虑2种材料的沉积面温度以及沉积面积s、s相等，且视角系数S 相同，则有

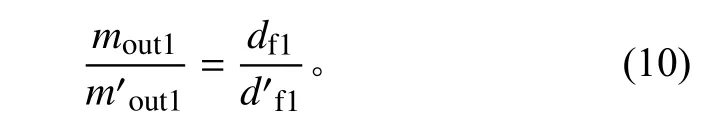
本文即利用式(10)计算在制备多层膜时2种污染源的实际沉积厚度。

2 试验研究

开展地面试验，研究非金属材料出气污染物对光学器件透射率和反射率的影响。首先基于ASTM E 595标准进行出气试验，然后采用分光光度计测量光学器件的透射率和反射率。

试验平台包括真空系统、温控系统、质谱计以及Lambda900分光光度计，其中，质谱计可测的质量数范围为0～300，Lambda900分光光度计可实现200～2500 nm 连续光谱的测量。

试验材料为信号电缆屏蔽线PVC材料外部绝缘层（以下简称PVC外皮）和3M公司的33+黑色绝缘胶带（以下简称绝缘胶带），均为航天器上常用的非金属材料，其出气污染物能在玻璃表面形成均匀污染膜，且出气量大，对玻璃片透射率有明显影响，因此对验证光学效应模型以及研究污染物对光学元件性能的影响具有很好的代表性。

为了研究非金属材料污染薄膜在紫外、可见光、红外不同波段对光学表面透射率的影响，分别选用在紫外波段工作的石英JGS1玻璃和可见光、红外波段工作的K9玻璃作为污染膜沉积基底。

试验过程如下：将PVC外皮、绝缘胶带（室温固化48 h）材料样品剪成小块放入样品舟内称重，2种材料各等量称重9份，样品净质量为PVC外皮(260±1)mg、绝缘胶带(210±1)mg。将试验材料与试验玻璃片一同放入低温凝结效应设备中，玻璃片中心正对样品舟下方的出气孔，首先在真空度10Pa、样品加热温度125℃、玻璃片温度25℃的条件下保持24 h，得到分别在石英玻璃、K9玻璃上沉积了1种材料的单层污染膜；更换样品取出部分玻璃片后保持上述试验条件，得到沉积了2种材料的污染膜。最终得到的污染膜种类见表1。

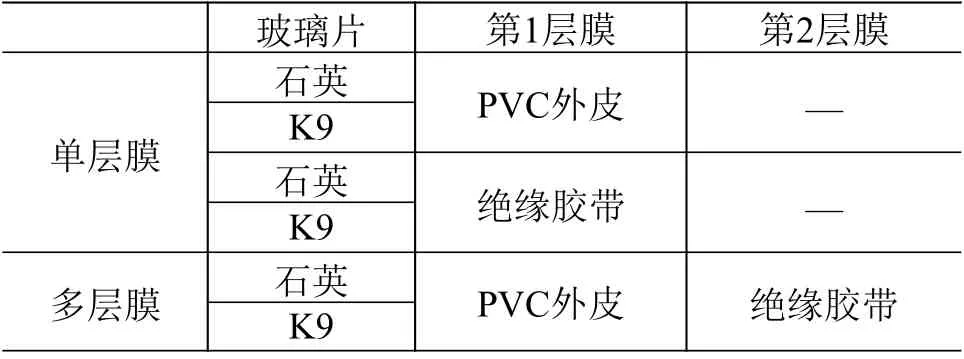
表1 不同基底污染膜种类Table 1 Types of contaminated films on different kinds of substrates

利用分光光度计测量沉积了污染膜后玻璃的反射率和透射率。以上过程重复3次取平均值。

3 计算结果与分析

本研究的最终目的是通过已知材料单层污染膜以及表面和过渡层的光学特性来计算由几种材料共同组成的混合污染膜的光学透射率。这部分工作分为2个步骤：

1）计算每层薄膜的厚度和光学常数。由1.2节可知，只要测量单层污染膜与基底正反两面的透射率和反射率并结合入射角，就可以获得该材料的光学常数与膜厚度，再结合质谱计所测的成分信息以及在制备多层膜和单层膜时的出气量就可以获得过渡层与表面的等效折射率以及多层膜中每层膜的实际厚度。

2）将已知条件代入混合薄膜光学特性计算程序中得到结果。将每层膜对应的n、k、d及入射角θ代入到多层薄膜透射率计算程序当中可计算出波长λ下对应的多层污染膜透射率，将透射率的计算值与实际测量值进行比较，可验证模型及计算结果的准确性。

3.1 红外波段混合污染膜透射率计算分析

3.1.1单层膜光学常数计算

分别根据K9玻璃基底上沉积PVC外皮出气污染物与绝缘胶带出气污染物的单层污染膜光谱透射率和反射率，由1.2.1节单层薄膜光学常数计算程序计算每种材料在红外波段的光学常数n、k 和膜厚度d。入射角θ=45º时，光学常数计算结果见图3和图4。

由图3可见：PVC外皮出气污染膜折射率n计算值在吸收峰波长位置对应处明显增大；20 000 nm 之后，随着波长增大，n值也增大。消光系数k值随波长的变化波动非常剧烈，尤其是在3400、5808、6837、7883、9000、9820、13 692 nm 等透射率和反射率强吸收峰处，k值急剧增大。

由图4可见：绝缘胶带出气污染膜折射率n计算值在2000～20 000 nm 红外波段基本保持稳定；20 000 nm 之后，随着波长增大n值缓慢增加。消光系数k值随着波长的增大而快速增大。

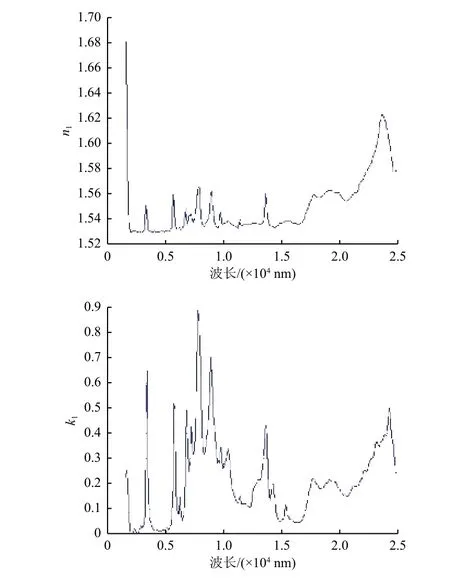
图3 K9玻璃基底沉积PVC外皮出气污染膜的光学常数计算值Fig.3 Calculated values of n1 and k1 of contamination film for PVC wire sheath deposited on K9 glasssubstrate

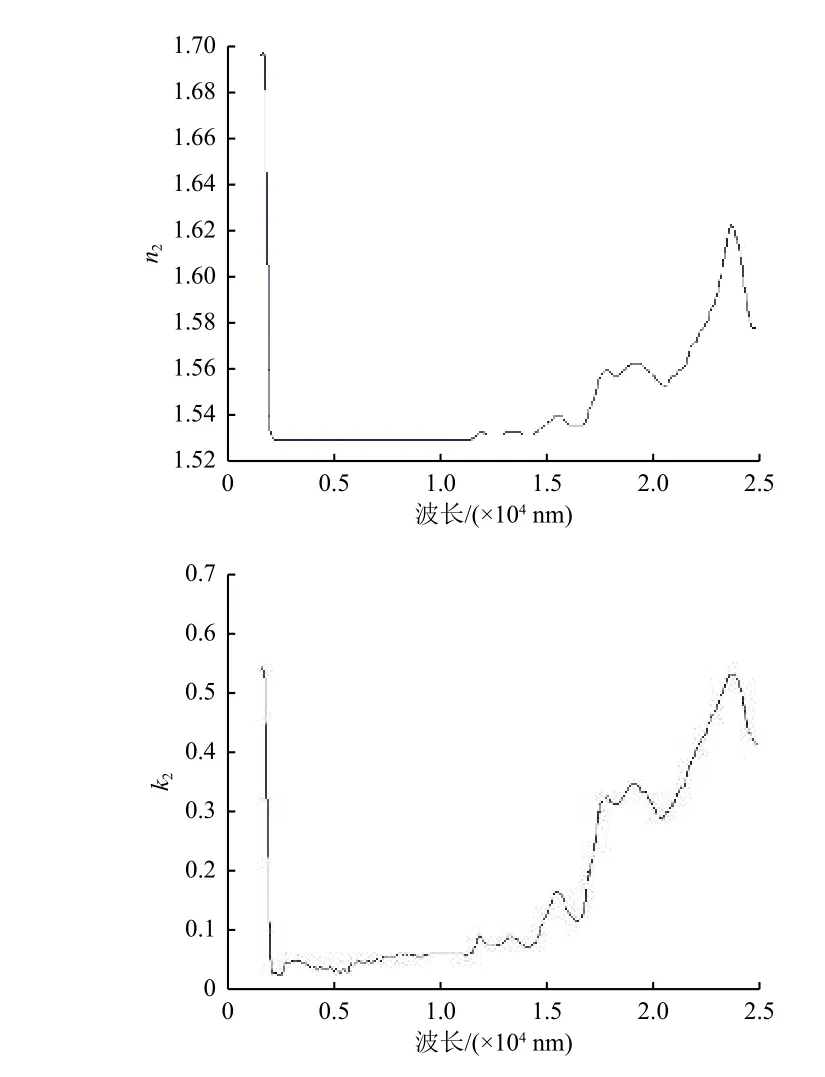
图4 K9玻璃基底沉积绝缘胶带出气污染膜的光学常数计算值Fig.4 Calculated values of n2 and k2 of contamination film for 3M tape deposited on K9 glass substrate

3.1.2过渡层以及粗糙表面光学常数的计算

根据1.2.2节，计算过渡层的光学常数n、k以及表面光学常数n、k，首先需要获得材料的平均分子质量和密度。在这里我们假设2种材料的平均分子质量和密度相同，得到过渡层的光学常数n和k如图5所示，并根据文献[15]的数据取过渡层厚度d=20 nm。

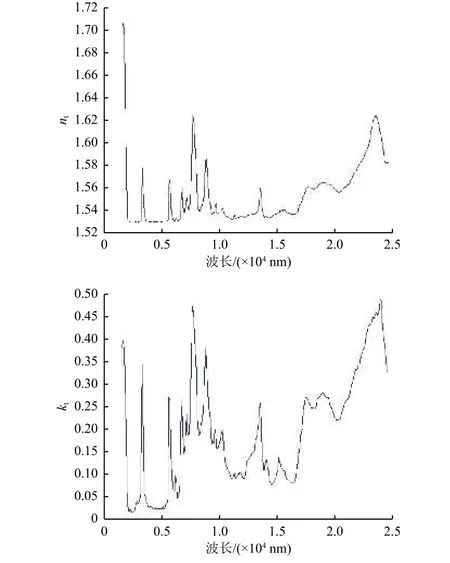
图5 污染膜过渡层光学常数计算值Fig.5 Calculated valuesof n t and k t of the transition layer

然后按照相同方法，将第1种物质替换为空气，便可以计算出表面的光学常数n和k（结果见图6），并取其厚度d=10 nm。污染膜总厚度为1.2μm，最后根据1.2.3节介绍的方法计算多层膜中每层膜的实际厚度。

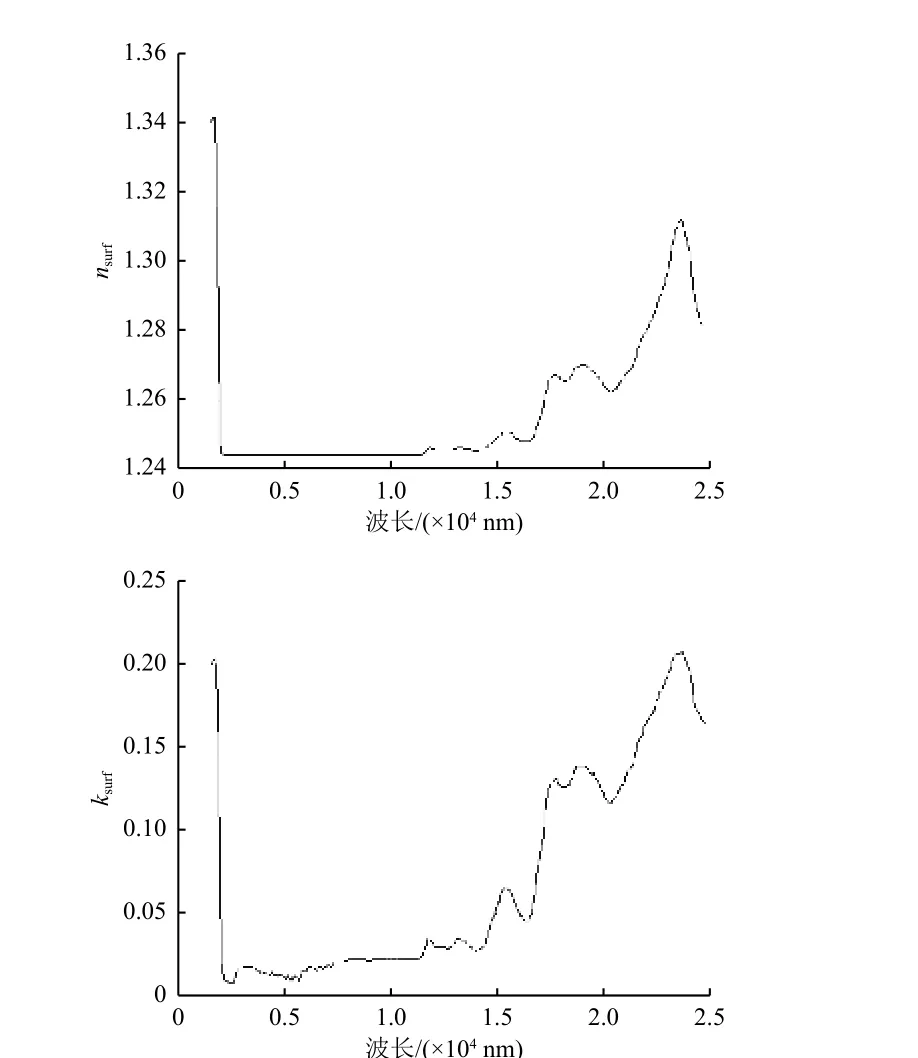
图6 污染膜表面光学常数计算值Fig.6 Calculated values of n surf and k surf of the rough surface

3.1.3 透射率计算值与试验测量值比较

图7是根据以上数据计算得出的室温下K9玻璃基底上混合沉积PVC外皮出气污染物、绝缘胶带出气污染物组成的污染膜透射率计算值与实际测量值。比较分析可以看出，计算值在曲线趋势上大致符合测量值，但在红外波段没有在紫外和可见光波段的符合性好，尤其是在11 500 nm 左右，计算值偏离测量值较远。计算值与测量值相比偏小，主要是因为在异位测量时引入新的污染物，导致计算的消光系数和折射率偏大，从而使得最终计算得到的透射率偏小。

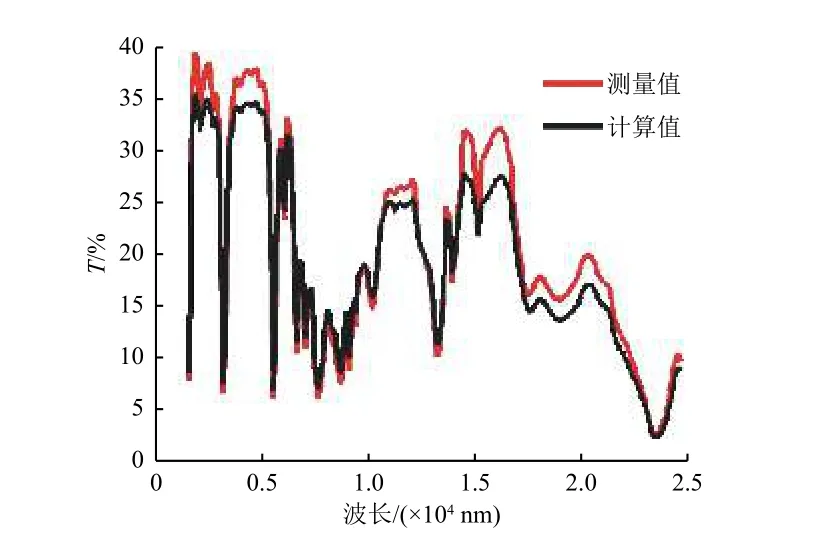
图7 K9玻璃基底上先后沉积PVC外皮出气污染膜与绝缘胶带出气污染膜后的透射率计算值与测量值Fig.7 The calculated and measured values of transmittance of the bilayer contaminated film deposited on K9 glass substrate(the first layer is outgassing contamination of the PVC shielding wire and the second layer is outgassing contamination of 3M tape)

3.2 可见光、近红外波段混合污染膜透射率计算分析

按照相同方法计算沉积在K9玻璃基底上的每种材料在可见光、近红外波段的光学常数n、k，以及过渡层和表面在这一波段的n、k，然后计算每层污染膜的实际厚度。图8是根据以上数据计算得出的室温下K9玻璃基底上依次沉积PVC外皮出气污染物和绝缘胶带出气污染物组成的混合污染膜的透射率计算值与实际测量值。比较分析可以看出，透射率计算值和测量值曲线趋势符合得非常好，但计算值比测量值偏小。

3.3 近紫外波段混合污染膜透射率计算分析

按照相同方法计算沉积在石英玻璃基底上的每种材料在近紫外波段的光学常数n、k，以及过渡层和表面在这一波段的n、k，然后计算计算每层污染膜的实际厚度。图9是根据以上数据计算得出的室温下石英玻璃基底上依次沉积PVC外皮出气污染物和绝缘胶带出气污染物组成的混合污染膜的透射率计算值与实际测量值。比较分析可以看出，透射率计算值和测量值曲线趋势符合得非常好，但计算值比测量值偏小，其原因可能是在建模的过程中假设同一种材料出气污染膜中间部分的折射率不随厚度发生变化，而实际每层膜中不同部位的折射率是存在差异的。

图8 K9玻璃基底先后沉积PVC外皮出气污染膜与绝缘胶带出气污染膜后的透射率计算值与测量值Fig.8 The calculated and measured values of transmittance of the bilayer contaminated film deposited on K9 glass substrate(the first layer is outgassing contamination of the PVC shielding wire and the second layer is outgassing contamination of 3M tape)

图9 石英玻璃基底先后沉积PVC 外皮出气污染膜与绝缘胶带出气污染膜后的透射率计算值与测量值Fig.9 The calculated and measured values of transmittance of the bilayer contaminated film deposited on the quartz substrate (the first layer is outgassing contamination of the PVC shielding wire and the second layer is outgassing contamination of 3M tape)