单元式轨道板温度翘曲应力计算方法研究
2021-03-14刘海涛宁娜王梦赵磊
刘海涛 宁娜 王梦 赵磊
中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081
单元式轨道板可有效释放长期整体温升温降引起的热胀冷缩作用力,但由于受太阳辐射、冷热循环等因素影响轨道板出现上下温差,从而产生翘曲和翘曲应力。单元式轨道板需承受温度梯度、列车荷载、轨下基础变形等多种因素作用,中国铁道科学研究院集团有限公司[1-4]、西南交通大学[5]、北京交通大学[6]等单位对轨道板力学性能进行了深入研究,分析了不同荷载对轨道板的作用效应,结果表明单元式轨道板翘曲应力为设计荷载效应的主要组成部分。EN 16432规定轨道板设计中应考虑温度循环作用下轨道结构温度梯度的影响,温度梯度效应计算可采用解析法或有限元法。中国标准TB 10082—2017《铁路轨道设计规范》规定了温度梯度具体取值,Q∕CR 9130—2018《铁路轨道设计规范(极限状态法)》建议温度梯度效应采用Westergaard 计算公式计算,我国高速铁路再创新阶段[7]也采用了该计算公式对轨道板进行设计。温度翘曲应力的计算方法主要有有限元法和基于Westergaard 计算公式的解析法[8-10]。本文对两种计算方法进行系统对比分析,从能否反映翘曲应力产生机理、是否考虑翘曲应力影响因素、两者计算结果的差异、工程验证等方面论证其适用性。
1 基于Westergaard 计算公式的温度翘曲应力计算方法
1.1 Westergaard计算公式
基于Winkler 弹性地基模型,Westergaard 研究了薄板的翘曲应力计算公式,假设:①薄板与地基始终紧密接触,无缝隙;②薄板内温度变化呈线性分布。
温度梯度作用下薄板内任一点的物理方程可表示为[11]
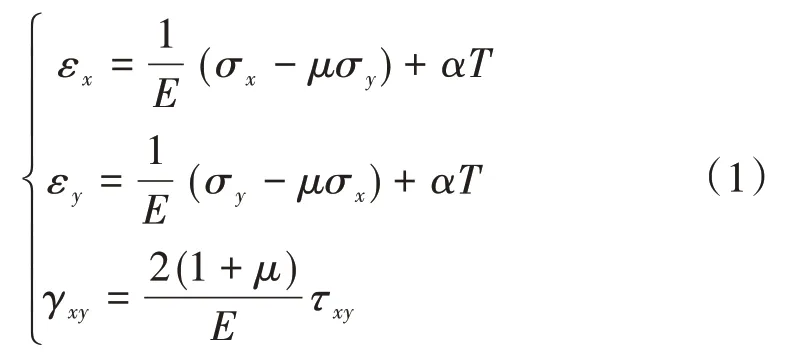
式中:α为薄板材料的线膨胀系数;T为薄板内任一点的温度变化值;E、μ分别为薄板材料的弹性模量和泊松比;εx、σx分别为x方向应变和应力;εy、σy分别为y方向应变和应力;γxy、τxy分别为xy平面剪切应变和剪切应力。
温度梯度作用下薄板内任一点的几何方程可表示为

式中:ω为z方向变形;Z为z方向距离。
由式(1)和式(2)可得

根据假设条件无限大板完全约束而无翘曲变形,故挠度ω= 0,曲率为0,即因此式(3)可写为
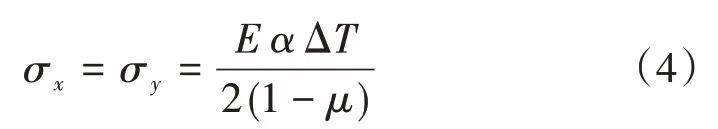
式中:ΔT为板顶与板底的温差。
对于长度为L、宽度为B的矩形板,引入泊松比得到板中及板边最大翘曲应力计算公式[12]。
板中最大翘曲应力为
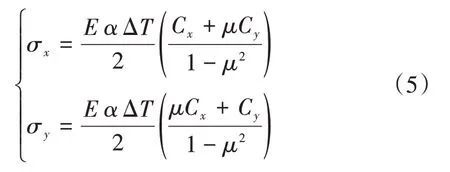
板边最大翘曲应力为
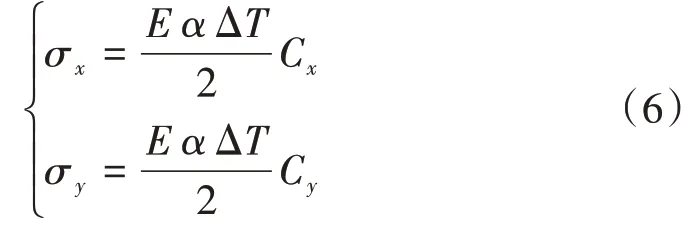
式中:Cx、Cy为翘曲应力系数。
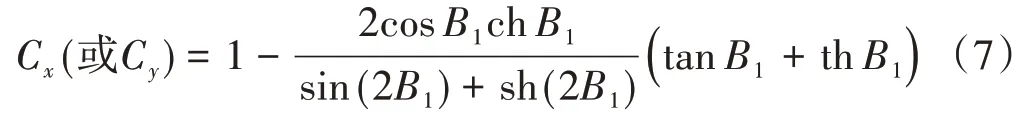
l的计算公式为
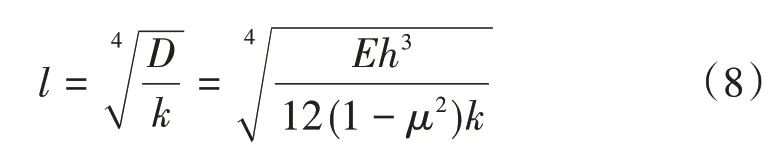
式中:D为矩形板的弯曲刚度;k为地基回弹模量;h为矩形板的有效厚度。
1.2 基于Westergaard 计算公式的解析法适用条件的有限元验证
分别采用基于Westergaard 计算公式的解析法和有限元法对单元式轨道板进行分析。采用实体单元建立有限元模型,根据解析法假设条件将单块轨道板放置于弹性地基上,轨道板与弹性地基之间设置为密贴关系,始终保持接触;从轨道板顶面到底面温度呈线性分布。轨道板采用C60 混凝土,板下支承面刚度取0.45 MPa∕mm。轨道板长5.6 m,宽2.5 m,厚300.0 mm。计算结果见表1。可见:前提条件一致的情况下两种计算方法得到的轨道板应力基本一致,其均可用于翘曲应力计算;解析法适用于轨道板与地基始终接触且温度呈线性分布的情况。

表1 解析法与有限元法的计算结果对比
2 轨道板温度翘曲应力产生机理
采用实体单元建立A、B、C、D 四个有限元模型。模型A 轨道板与弹性地基始终保持接触,从轨道板顶面到底面温度呈线性分布,不考虑轨道板自重;模型B(图1)是在模型A 的基础上取消轨道板与基础之间的密贴关系,采用接触关系,接触状态随翘曲变形而变化,仅施加线性温度荷载,不考虑轨道板自重;模型C在模型B 的基础上考虑轨道板自重;模型D 在模型C的基础上设置温度荷载呈非线性分布,温度按厚度的1.3 次幂变化,且温差保持一致,顶面变化快,底面变化慢。
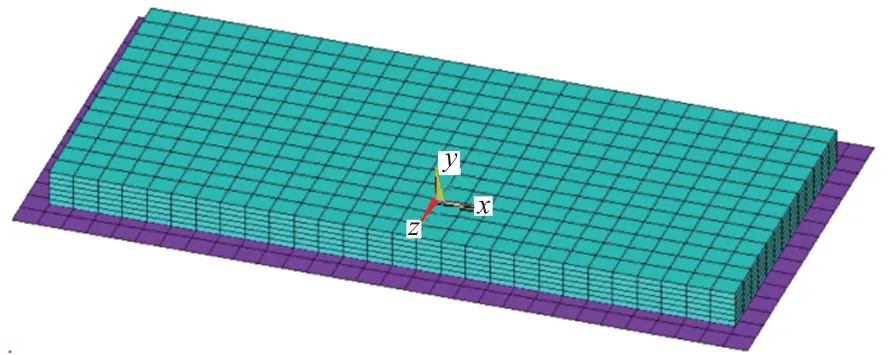
图1 模型B
模型B、模型C、模型D中正温度梯度下板中上翘,板边下挠,仅板边与基础接触,见图2。
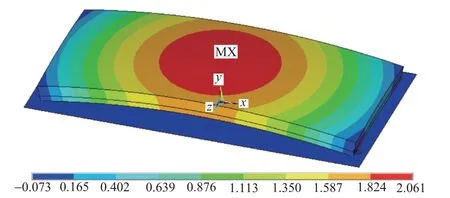
图2 模型B在正温度梯度下的竖向位移(单位:mm)
负温度梯度下板中与基础接触,板边上翘。单块轨道板不同边界和温度梯度下翘曲应力与位移见表2。对于应力“∕”之前为拉应力,之后为压应力;对于位移“∕”之前为向上位移,之后为向下位移。

表2 单块轨道板不同边界和温度梯度分布下翘曲应力与位移
由表2 可知:模型B 状况下并不产生应力;轨道板的重力(模型C)将轨道板下压,轨道板产生应力;当轨道板内温度呈非线性分布(模型D)时,由于上下层间的约束同样也产生应力。
轨道板温度翘曲应力产生的本质是热胀冷缩使结构发生变形,引起边界条件变化,而荷载(含自重)、温度非线性分布等因素约束轨道板的自由变形,从而产生轨道板温度翘曲应力。随约束作用的增强,应力逐渐增加,变形逐渐减小。基于Westergaard 计算公式的解析法采用最极端的约束,即轨道板完全受地基的约束,变形较小,但应力太大,无法反映轨道板结构真实受力,其将自由状态下的温度应变直接作为翘曲应力对应的应变不符合实际情况。
3 轨道板温度翘曲应力影响因素
轨道结构为多层多部件的系统结构,轨道板温度翘曲应力同时受其他部件(如限位装置和扣件)的约束作用、轨道板重量、板下基础刚度等影响。以高速铁路CRTSⅢ型轨道结构为例,研究各因素对轨道板温度翘曲应力的影响规律,验证基于Westergaard 计算公式的解析法和有限元法对影响因素的敏感性。温度梯度取45 ℃∕m,除特殊说明外不考虑温度梯度随厚度的折减。
3.1 轨道结构部件对温度翘曲应力的影响
不同于单块轨道板,轨道结构中的轨道板受限位装置、钢轨扣件等部件的约束。首先建立放置于底座上的单块轨道板模型(单板模型),轨道板与底座之间采用土工布隔离;然后在单板模型基础上增加凸台和凹槽限位(凸台模型),凸台和凹槽限位之间设置弹性缓冲垫层;最后增加钢轨和扣件(足尺模型),研究限位和扣件约束对轨道板翘曲应力的影响。
计算结果见表3。可见:①有限元法能够反映凸台、凹槽限位和扣件对轨道板的约束作用,翘曲应力随约束部件增多而逐步增加,增加钢轨和扣件(足尺模型)后应力最大;②解析法无法反映凸台、凹槽限位和扣件对轨道板翘曲应力的影响;③由于解析法假设轨道板和基础密贴,采用了最大约束,将温度应变完全转化为应力,故其解大于有限元解。

表3 不同模型下轨道板温度翘曲应力 MPa
3.2 轨道板重量对温度翘曲应力的影响
轨道板其他条件相同,轨道板重量不同将改变轨道板翘曲后的下压力,温度翘曲应力也将不同。轨道板密度分别取1 500、2 000、2 500、3 000 kg∕m3,计算结果见表4。可见:解析解大于有限元解;有限元法计算所得的翘曲应力随轨道板密度增加而逐渐增大;解析法无法反映轨道板重量的影响。
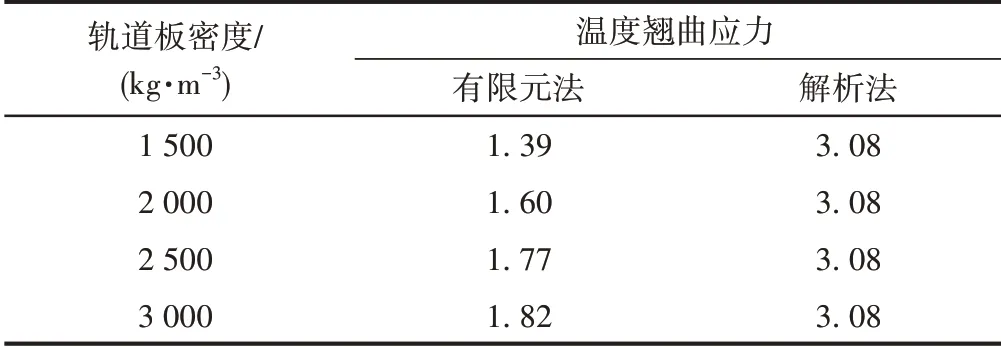
表4 不同轨道板密度下轨道板温度翘曲应力 MPa
3.3 轨道板下支承面刚度对温度翘曲应力的影响
采用足尺模型研究轨道板下支承面刚度对轨道板温度翘曲应力的影响。轨道板下支承面刚度分别取0.01、0.02、0.03、0.10、0.30、1.00、2.00 MPa∕mm,考虑轨道板上下温差随厚度折减,计算结果见图3。可见:两种方法计算所得的轨道板温度翘曲拉应力随支承面刚度增加而增大,支承面刚度小于等于0.30 MPa∕mm 时轨道板温度翘曲应力急剧增加,支承面刚度大于0.30 MPa∕mm 时轨道板翘曲应力增加缓慢。两种计算方法均能反映轨道板下支承面刚度对温度翘曲应力的影响,解析法计算所得的温度翘曲应力变化更为剧烈,其值明显大于有限元法计算值。
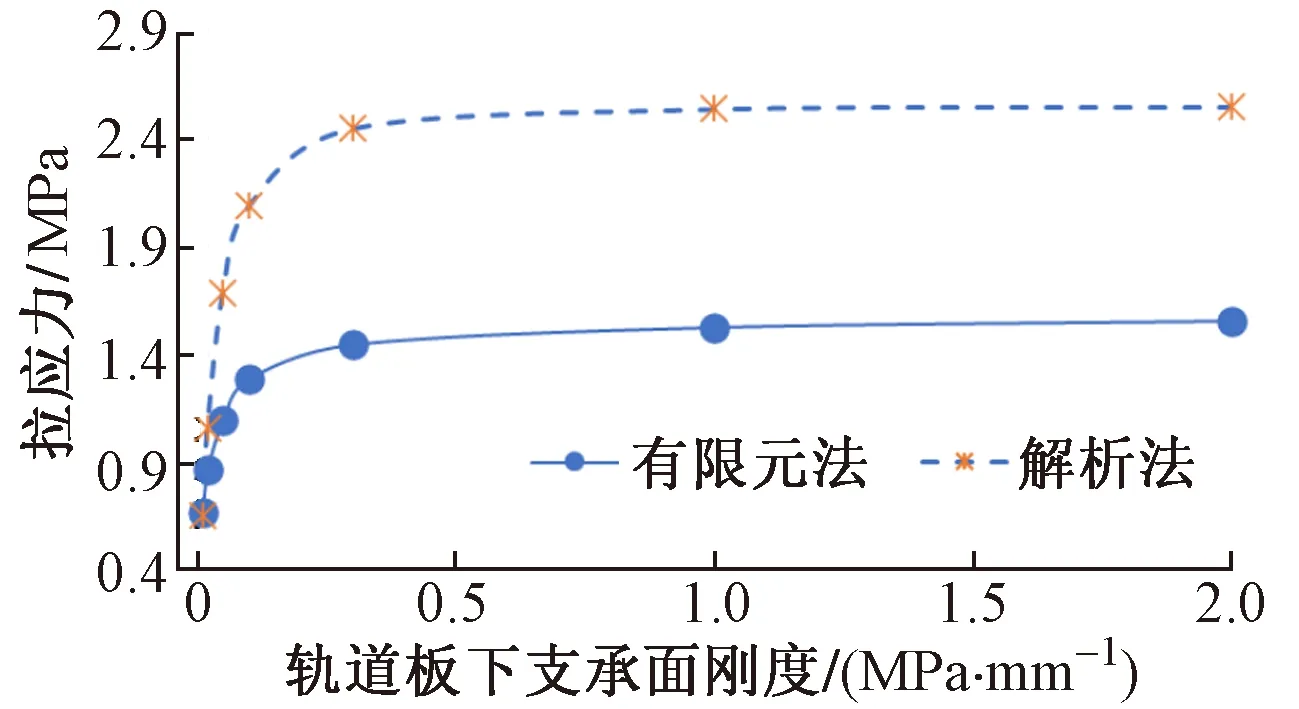
图3 轨道板温度翘曲拉应力随支承面刚度变化曲线
4 轨道板温度翘曲应力工程验证
在西宝(西安—宝鸡)客运专线CRTSⅢ型先张法板式无砟轨道试验段对轨道板翘曲应力进行了测试。轨道板底自密实混凝土应变、温度梯度时程曲线见图4。可见:轨道板温度梯度为61 ℃∕m 时,板底自密实混凝土最大应变为34.7×10-6,对应的翘曲拉应力为1.18 MPa;温度梯度为-15 ℃∕m时,混凝土最大应变为11.2×10-6,对应的压应力为0.38 MPa。测试位置距板底50 mm,换算到板底位置拉应力为1.74 MPa,压应力为0.56 MPa。
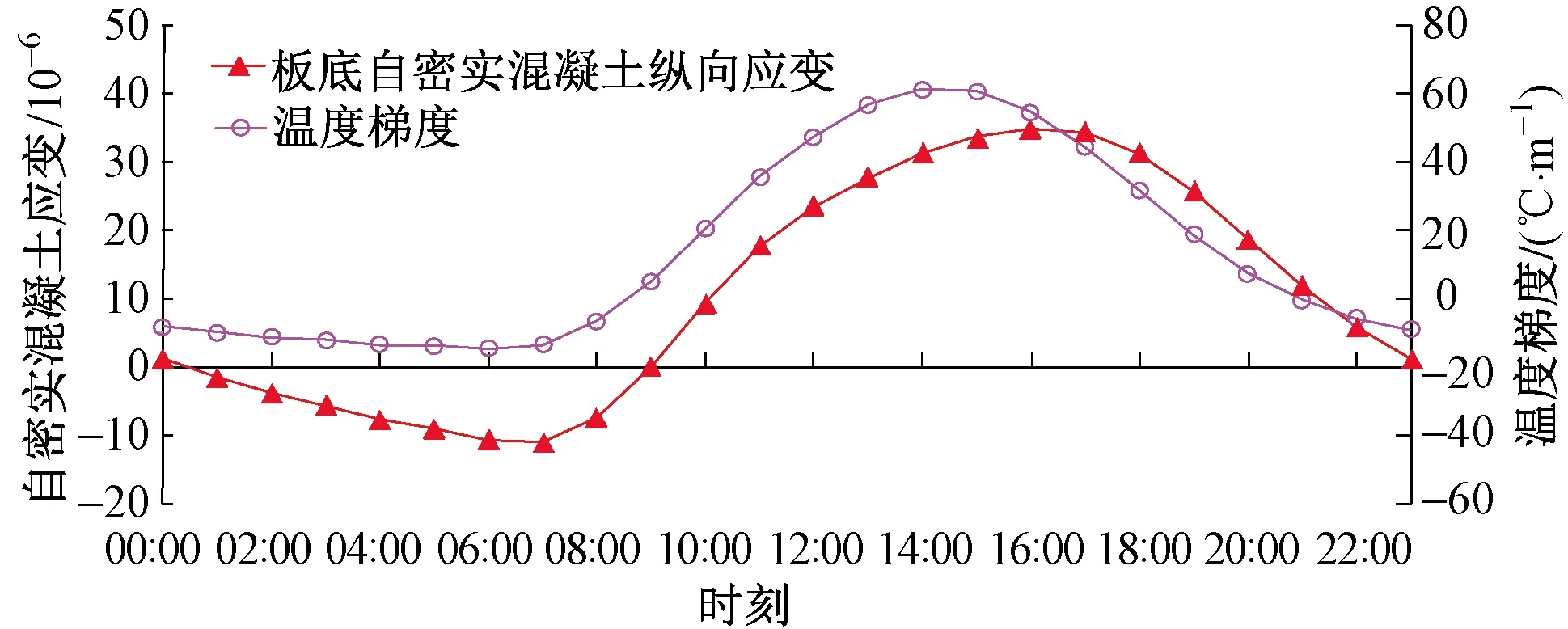
图4 轨道板底自密实混凝土应变、温度梯度时程曲线
有限元法温度梯度呈非线性分布,分别采用基于Westergaard 计算公式的解析法和有限元法计算温度翘曲应力,结果见表5。可见:解析法计算值明显偏大,有限元法计算值与实测值较接近,证明采用有限元法分析轨道板翘曲应力计算结果更可靠。
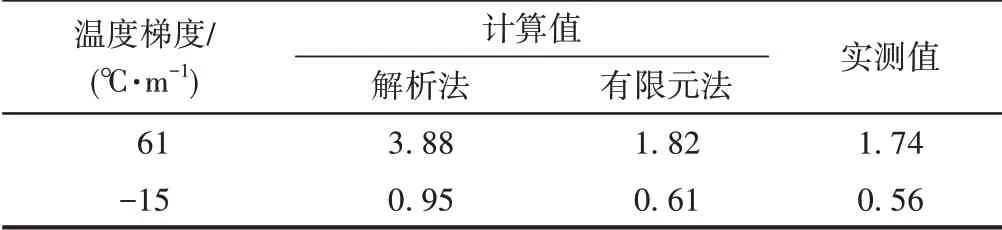
表5 不同方法温度翘曲应力计算值与实测值对比MPa
5 结论
1)基于Westergaard 计算公式的解析法假定轨道板与基础始终保持接触状态,不符合翘曲变形实际情况。该方法假定温度梯度产生的应变导致了翘曲应力,不符合翘曲应力产生机理。
2)当有限元法与解析法前提条件一致时,计算结果一致。采用有限元法再现了轨道板翘曲应力产生过程,在温度梯度作用下轨道板自由翘曲变形、忽略任何约束(包括自重)时不产生翘曲应力,此时轨道板与基础接触状态发生改变;在轨道板自重及其他约束作用下轨道板产生翘曲应力。
3)凸台和凹槽限位、钢轨和扣件、轨道板重量约束轨道板的变形,影响翘曲应力,但解析法无法反映。两种方法轨道板下支承面刚度对温度翘曲应力的影响规律较为一致,但解析法计算值比有限元法大。
4)经工程验证,正负温度梯度下有限元法温度翘曲应力计算值与实测值较接近,解析法计算值偏大。
5)轨道板温度翘曲应力求解为复杂的随动超静定结构求解,难以采用解析法进行精确分析。基于Westergaard 计算公式的解析法适用条件、考虑的影响因素、计算结果均难以满足轨道板翘曲应力计算。建议轨道板翘曲应力求解采用有限元法。
