异类细胞单元构型策略与装配研究

吕晶薇 高语斐 戴野 刘朝旭 齐云衫 张瀚博

摘 要：针对空间设施建设的问题，基于机器人系统的多层次理论，设计了四种空间桁架在轨组装机器人的异类细胞单元模块，构建了满足于空间桁架在轨组装的多种机器人构型方案。对多种空间桁架在轨组装机器人构型进行了运动学仿真分析，得到机器人在桁架组装过程中，其关节旋转运动和装配运动的相关轨迹曲线，搭建了机器人的运动学实验平台，分析实验产生误差的原因。验证了机器人运动性能的可靠性与桁杆组装的准确性，探讨了机器人运动误差和对桁杆装配精度的影响。研究结果可为空间桁架在轨组装异类细胞单元衍生构型与装配提供一种理论和技术支持。

关键词：运动学;构型方案;协同组装;空间桁架;细胞单元

DOI：10.15938/j.jhust.2021.06.008

中图分类号： V11

文献标志码： A

文章编号： 1007-2683（2021）06-0055-11

Study on Cell Configuration Strategy and On-orbit

Assembly of Heterogeneous Cells

L Jing-wei， GAO Yu-fei， DAI Ye， LIU Zhao-xu， QI Yun-shan， ZHANG Han-bo

（1.Beijing Satellite Manufacturing Co.， Ltd.， Beijing 100094， China;

2.Key Laboratory of Advanced Manufacturing Intelligent Technology of Ministry of Education， School of Mechanical and Power Engineering，

Harbin University of Science and Technology， Harbin 150080， China;

3.Institute of Digital Design and Automatic Machinery Product Development， School of Mechanical and Power Engineering，

Harbin University of Science and Technology， Harbin 150080，China）

Abstract：Aiming at the problems of space facilities construction， based on the multi-level theory of robot system， four kinds of heterogeneous cell modules of space truss on-orbit assembly robots were designed， and a variety of robot configuration schemes for space truss on-orbit assembly were constructed. The kinematics simulation analysis was carried out for various space truss in-orbit assembly robots， and the relative trajectory curves of joint rotation and assembly motion were obtained during the truss assembly process. The kinematics experiment platform of the robot was built， and the causes of experimental errors were analyzed. The reliability of the robot motion performance and the accuracy of the truss assembly are verified， and the influence of the robot motion error and the truss assembly accuracy is discussed. The results of this study can provide a theoretical and technical support for the configuration and assembly of heterogeneous cell derived from space truss in-orbit assembly.

Keywords：kinematics; configuration scheme; collaborative scheme; space truss; cell unit

0 引 言

航天技术经过半个多世纪的发展和实践，人类在认识空间，进入空间和利用空间的技术层面上取得了初步成果。目前，随着大型空间结构的规模、在轨操作量级以及任务复杂程度急剧增加，大尺寸的空间设施难以一次性发射升空，需分模块发射后进行在轨装配[1-4]。由于大型空间设施的功能及其内部结构复杂化，传统的空间机械臂或转位机构在完成大型空间设施的在轨组装任务时，越来越显现出局限性，在这种条件下，一种专用于大型空间设施舱段之间连接桁架的在轨组装机器人应运而生[5-7]。

空间桁架在轨组装机器人是一种多层次可重构的模块化空间细胞机器人，具有灵活性、完备性、自主性等特点，可以灵活的根据在轨操作任务的变化，通过细胞单元的重構组合，衍生出多种结构构型的空间操控机构[8]。当其中某一模块发生故障时，可以通过重构功能利用功能相同的模块替换失效模块，从而保证任务继续执行，特别适用于未来航天任务中大型空间设施建设与在轨组装的任务中[9-12]。

由于空间桁架在轨组装机器人由多种异类细胞单元模块组成，如何根据在轨任务的变化，转变和生成相应的机器人在轨工作构型，是当前需要解决的问题之一。针对这个问题，国内外学者对机器人的重构方法进行了大量的研究。

日本名古屋大学提出了一种名为CEBOT[13-14]的异构细胞体模块机器人，该机器人由分级的易异构系统构成，为了解决机器人重构的问题，他们提出了分布式遗传法，在之后又提出了“熵最大原则”和“熵最小原则”两种重构方法分别用于解决多种复杂和简单少量的机器人工作任务[15]。美国南加利福尼亚大学提出了一种模块化自重构机器人的最优重构规划方法（ORP），其目标是找到将一个任意配置的可重构模块转化成另一个的最短重构序列，该方法包括“MDCOP算法”和“GreedyCM算法”，前者用于找寻初始配置到最终配置的最大匹配边，生成基于图论的最优重构步骤，后者可以在时间多项式中找到一个近似的最佳重构方案[16-17]。

天津理工大学提出了一种基于SCM拓扑空间连接矩阵的无编号分布式重构策略。该方法根据一种名为M2sbot单元模块的结构特点，在重构过程中，通过遍历顺序找到不需要重构的公共拓扑，按照根节点连接器的顺序通过深度优先搜索算法进行重构。该重构方法不仅降低了重构的复杂度，而且可以在图形界面实现人机交互，对动态环境实时监控[18-19]。上海交通大学提出了一种逐步填充式自变形方法对名为M-cube的单元模块进行自重构运动规划，逐步填充式自变形算法将当前构型与目标构型的重心之间的距离函数定义为每个模块的运动启发信息，再根据模块自身的运动空间预测分析，使驱动模块不断向目标位置运动，最终填满目标构型[20]。该种方法可以根据该模块运动特点，填充时按照“先下后上，先里后外”的原则，先填充目标区域的底部和里部区域，保证自变形过程顺利实现，使其能够快速完成该类自重构模块化机器人系统的自变形任务[21-22]。

目前国内外对空间在轨操作机器人重构方法仅限应用于其自主设计的机器人单元模块，不具有通用性。本文在空间桁架在轨组装机器人的基础上，以空间桁架组装任务为背景，提出一种用于空间桁架在轨组装机器人细胞单元模块重构和机器人构型转化的重构策略方法，并进行理论延伸，使其具有通用性，以适用于不同类型的模块重构和构型转化的机器人重构任务中。

1 空间桁架在轨组装机器人

1.1 空间桁架在轨组装机器人组成

空间桁架在轨组装机器人是一种多层次的模块化机器人，主要由多种异类细胞单元模块构成，能够在微重力轨道环境中，根据空间桁架在轨组装任务的需要，通过异类细胞单元模块的重构组合，衍生出多种在轨协同操作的机器人构型，以完成机器人在桁架上的移动、抓持、传递、组装等一系列的空间桁架组装工作，具有灵活性、完备性、自主性等特点，多种异类细胞单元模块可以分为细胞质单元模块、转动细胞模块、夹爪功能和旋转功能等模块。

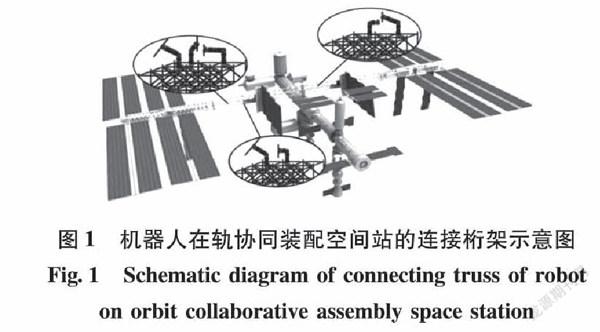
由于空间桁架体量和尺寸较大，传统的单机器人装配方式满足不了空间桁架组装要求，针对该问题，本文采用扩展式的空间桁架组装方式，将空间桁架进行模块化的区域划分，并结合多种构型机器人协同在轨组装的工作形式，将桁架有规律的进行延伸组装，以完成大体量空间桁架的装配任务。机器人在轨协同装配空间站的连接桁架示意图，如图1所示。

1.1 空间桁架的构型分析

空间桁架作为空间站的重要组成部分，应具有强度高、易组装、结构稳定等特点。本文为了保证空间桁架的稳定性能，在现有桁架构型的基础上创新设计了一种可延伸的三棱柱空间桁架构型。三棱柱空间桁架作为整体桁架组成的最小单元，可以延伸装配，利用桁杆和球头的不断堆叠，最终将完成整个空间桁架的组装。这种空间桁架结构由于具有质量轻、拆装灵活、承载能力强、可在轨组装、在轨重构等特点，既可以作为航天器的主体承力结构，又可以作为有效载荷的支撑结构，未来将会广泛应用于航天工程领域中。

空间桁架具体结构由桁杆、球头、自动锁紧装置、径向和轴向连接头组成。本文创新的采用了一种侧推式的空间桁架的组装形式，能够借助桁架中桁杆和连接球头本身的锁紧机构，可以避免复杂的桁架组装流程，以完成桁杆的装配工作。

创新设计的自动锁紧装置是连接球头与径向连接头的重要组成部分。在进行空间桁架单个桁杆的组装过程中，自动锁紧装置可以在桁杆的径向连接头靠近时，通过锁紧装置中设有的弹簧卡夹，可以自动完成组装桁杆的锁紧工作;同时，球头作为桁架节点，其组装原理与单个桁杆的组装原理相似，利用自动锁紧装置末端的长销与球头中的销孔相连并锁紧，即可完成球头节点的组装。

因此，在失重和无介质环境中，根据动量守恒定律，无论装配任何方向的桁杆和球头节点，只需要通过在轨工作的机器人将桁杆和球头节点装配到自动锁紧装置中，即可完成空间桁架的组装工作。

1.2 协同组装机器人的构型分析

空间桁架在轨组装机器人在桁架装配的过程中主要实现以下3大功能：一是对桁架进行组装;二是能够在桁架上进行桁杆等零件的搬运;三是抓取桁杆等零件，对其进行相对安装位置的调整。

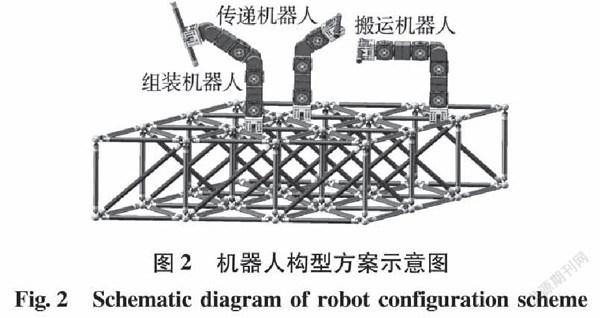
在空间桁架的组装任务中，采取多机器人协同装配的扩展式桁架的组装方式，主要通过搬运机器人、传递机器人和组装机器人3种机器人配合工作，形成一个机器人团队，初步的构型方案如图2所示。

搬运机器人主要负责桁架零件的搬运工作，需要把桁杆从零件库中进行提取，并搬运给下一工位的传递机器人进行桁杆的传递，是空间桁架组装的第一步;传递机器人主要负责对桁杆进行传递，需要把桁杆从上一工位的机器人夹爪中进行抓取传递，抓取后再传递给下一工位的机器人，隨着桁架的组装扩展，传递机器人的在轨工作数量逐步增加，是空间桁架组装的重要纽带;组装机器人负责把上一工位机器人传递的桁杆零件进行抓取，并根据组装要求进行桁杆的装配，是空间桁架在轨组装任务中最重要的功能机器人。

根据机器人的构型设计方案可知，3种空间桁架在轨协同组装机器人的结构构型由不同数量和功能的细胞单元模块组成，3种机器人的功能实现均依靠相应的关节模块完成预定的执行操作。通过对不同功能的机器人构型方案进行分析，得到机器人的基本构型参数如下表1所示。

由表1可知，3种功能机器人均由细胞质单元模块、转动细胞模块和夹爪功能模块构成，但不同功能机器人的单元模块组成数量是不同的。这种机器人构型的结构设计，可以使机器人具有不同的操作自由度，以最大化的满足于机器人操作功能的实现。3种协同组装机器人的构型简图如图3所示。

由上表2可知，3种不同功能机器人完全舒展达到最大尺寸时，各个关节旋转角度的基本运动参数。根据三种机器人的结构构型、运动方式和相关尺寸参数计算可以得出，搬运机器人完全展开时机械臂长度为900mm，传递机器人机械臂的最大伸展长度为500mm，组装机器人机械臂的最大伸展长度为900mm。

如图4所示，当机器人在轨协同组装团队中包含1个传递机器人作为桁架零件的传送纽带时，最大可以组装尺寸长度为3700mm的空间桁架。每增加1个传递机器人作为桁架零件的传递纽带时，空间桁架的尺寸长度可以扩展增加1000mm。因此，根据空间桁架的组装需要，增加或减少在轨工作的机器人数量，即可完成不同尺寸的空间桁架的组装工作。

2 机器人桁架组装的运动学分析

运动学是开展空间桁架在轨组装机器人特性分析的基础。本文主要通过分析机器人在轨协同组装的运动形式，对机器人在轨组装运动过程进行计算机模拟，得出机器人在进行桁架装配工作时，其转动关节驱动桁杆的位置、速度、加速度等变化曲线，验证机器人运动性能的稳定性与桁杆组装的准确性。

2.1 机器人坐标系的建立

空间桁架在轨组装机器人的三维模型如图5所示。为了描述机器人相邻关节之间的运动关系，采用D-H参数求解方法建立机器人各个关节的连杆坐标系，如图6所示。

具体的组装机器人D-H参数如下表3所示：

2.2 机器人的运动学方程

根据机器人建立的关节坐标系和相关的D-H参数，可以通过建立机器人的运动学方程，求解机器人末端关节相对参考系的运动位姿。

机器人的齐次变换矩阵A为

An+1=nn+1T=cosθn+1-sinθn+1cosαn+1sinθn+1sinαn+1an+1cosθn+1

sinθn+1cosθn+1cosαn+1-cosθn+1sinαn+1an+1sinθn+1

0sinαn+1cosαn+1dn+1

0001（1）

机器人主要利用构型中的摆转和旋转关节模块驱动末端夹爪进行相关的运动操作，本文通过结合坐标系的相关参数和齐次变换矩阵方程，对不同转动关节进行求解，可以求得：

1）旋转关节1的齐次变换矩阵：

A1=01T=cosθ1-sinθ100

sinθ1cosθ100

0010

0001（2）

2）旋转关节2的齐次变换矩阵：

A3=23T=cosθ3-sinθ30a3cosθ3

sinθ3cosθ30a3sinθ3

001d3

0001（3）

3）摆转关节1的齐次变换矩阵：

A2=12T=cosθ20-sinθ2a2cosθ2

sinθ20cosθ2a2sinθ2

0-100

0001（4）

4）摆转关节2的齐次变换矩阵：

A4=34T=cosθ40-sinθ40

sinθ40cosθ40

0-100

0001（5）

因此，通過齐次变换矩阵可以得到多自由度的机器人正向运动学表达式为04T=A1A2A3A4。

2.3 机器人的组装运动分析

对机器人模型进行运动过程的分析，如图7所示。

由图7可以看出，机器人在指定的初始位置正处于待命状态，当接收到上一工位机器人的信号时，其构型中的摆转和旋转关节开始转动，带动末端夹爪到达相应位置进行桁杆的抓取，此时末端夹爪张开，并在桁杆的定点位置准确的完成桁杆的抓取;桁杆抓取后，上一工位机器人在其旋转关节的带动下，与桁杆分离，完成桁杆的传递工作;机器人完成桁杆抓取后，其构型中的摆转和旋转关节开始协同转动，进行桁杆装配位置的的调整;调整位置后，机器人通过相关转动关节的带动下，在准确的位置完成桁杆的装配工作。

2.4 机器人运动学仿真结果及分析

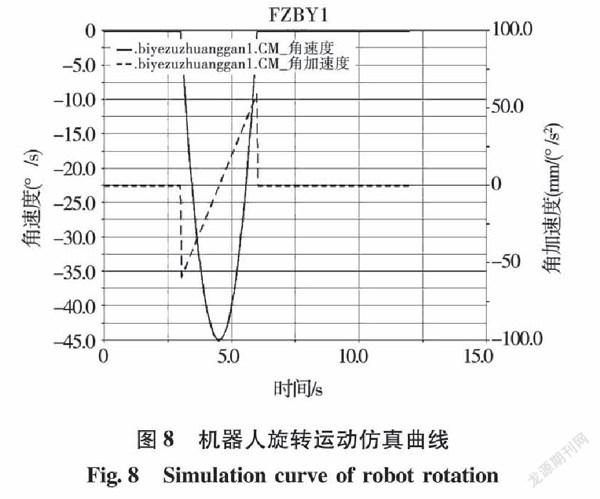
机器人在理想状态下进行空间桁架在轨装配时，末端夹爪所夹取的桁杆轨迹决定了桁杆组装的准确性，机器人装配运动决定了桁杆组装的精确度。通过运动学分析，得出机器人旋转运动的角速度与角加速度变化曲线，如图8所示。

由图8可知，3s时桁杆在机器人第二旋转关节的带动下开始在z轴方向进行旋转运动，6s时桁杆调整到相应的空间位置上，4.5s时角速度达到最大，角速度与角加速度的曲线是同步变化的，桁杆的旋转运动平稳，符合运动规律。

代表机器人装配运动的角速度与角加速度变化曲线，如图9所示。

由图9可知，6s时桁杆在机器人180°摆转关节的带动下开始在y轴方向进行旋转运动，12s时将桁杆装配在桁架的指定位置上，9s时角速度达到最大，角速度与角加速度的曲线是同步变化的，桁杆的装配运动过程平稳，符合桁杆装配的运动规律。

机器人桁架组装角速度与角加速度变化曲线，如图10所示。

由图10可知，0～3s内机器人正处于待命状态，当上一工位机器人在3s内完全脱离桁杆后，机器人开始进行组装运动;3s时桁杆在z轴方向进行旋转，6s时旋转到相应位置，其余方向均无运动;6s时桁杆在y轴方向进行旋转运动，12s时桁杆到达桁架指定位置进行装配，其余方向均无运动。从图10中的结果曲线可以看出，机器人桁架组装的总体运动只包含在z轴和x轴做阶段性的转动，其角速度与角加速度的曲线均变化平稳且曲线同步，因此，机器人桁架组装的总体运动过程平稳，符合运动规律。

机器人桁架组装位移与速度变化曲线，如图11所示。

由图11可知，0～3s时桁杆处于待命状态，3～6s时桁杆在机器人第二旋转关节的带动下进行旋转运动，4.5s时达到最大速度，并且桁杆的中心点在x轴的方向发生变化;6～12s时，机器人通过180°摆转关节开始进行转动，将桁杆装配到空间桁架的指定位置上，此时桁杆的中心点随着关节的转动在x轴方向发生变化，12s时到达准确的装配位置，完成桁杆的安装。从图11中的结果曲线可以看出，机器人桁架组装的位移和速度的变化平稳，在12s时，桁杆准确的到达装配位置且速度减小为0，避免了桁架装配时发生碰撞，符合机器人组装运动规律。

综上所述，由机器人运动学仿真结果可以得到，通过上一工位机器人将桁架零件进行传递后，机器人在12s时即可完成桁杆的组装工作，机器人旋转运动在4.5s时角速度达到最大，机器人装配运动在9s时角速度达到最大，并且在机器人运动过程中角速度与角加速度同步变化，在组装过程中各个关节的总体运动平稳，并且桁杆到达空间桁架指定装配位置的同时，速度减小为0，避免了机器人在桁杆组装过程中发生碰撞，桁杆组装的准确性能够达到设计要求，符合桁杆装配的运动规律。

3 机器人桁架组装的实验研究

为了验证空间桁架在轨组装机器人的运动性能，本文在不同功能机器人构型的基础上，对机器人桁杆传递运动和桁架组装运动的准确度进行了实验研究。通过与机器人运动学仿真结果做对比，验证在组装桁架过程中不同功能机器人运动过程的合理性与桁杆装配的准确性。

3.1 实验平台搭建

空间桁架在轨组装机器人由多个细胞单元模块组成，每个单元模块均由单独的电机控制。由于细胞质单元模块是连接机构，在实验中主要起连接功能模块的作用，因此，在实验的过程中，可以忽略细胞质单元模块中的电机控制。根据桁架组装的实验要求，只需要协同控制机器人构型中转动功能模块的驱动电机即可。

机器人桁架组装的实验平台主要由计算机和中继单元组成。计算机主要进行电机控制变量的输入、储存和通讯等工作;中继单元由12V电源模块、Arduino控制模块和电机驱动模块TMC2208组成，主要接收计算机发出的驱动控制指令，同时为转动关节模块中的电机提供电源，并对电机进行驱动控制，从而实现机器人完成特定的运动。

3.2 机器人位置精度实验

在实验中，机器人的每个细胞单元模块均采用3D打印技术进行制造，其打印精度可达到0.05mm。由于3D打印机打印出的细胞单元模块具有较高的制造精度，在实验的过程中机器人构型的装配误差可忽略不计，因此，无论是模块的制造误差还是机器人的装配误差均对机器人位置精度实验的结果影响较小。

機器人在进行桁杆传递运动时，有典型的4种位置变化，如图12所示。

理论上，当机器人末端夹爪中的机械抓取手抓取桁杆时，桁杆径向中心距离末端夹爪底面的距离为150mm。可以通过分析传递机器人所抓取的桁杆径向中心在4种典型位置上理论与实际的偏差，计算出机器人桁杆传递的位置精度。

由图12可知，理论上当传递机器人构型中的180°摆转单元模块转动30°时，桁杆的径向中心点与机器人轴线的距离为225mm;当180°摆转单元模块转动90°时，桁杆径向中心点与机器人轴线的距离为0mm;当180°摆转单元模块转动150°时，桁杆径向中心点与机器人轴线的距离为225mm;当180°摆转单元模块转动180°时，桁杆恰好传递到指定位置，等待组装机器人的抓取，此时，桁杆径向中心点与机器人轴线的距离为450mm。

机器人的位置精度实验过程，如图13所示，实验以理论上桁杆径向中心点与机器人轴线的距离为基准，根据传感器多次测量桁杆径向中心位置与理论值的实际偏移量，通过计算获得传递机器人构型中的180°摆转单元模块分别转动30°、90°、150°和180°时，桁杆径向中心点与机器人轴线的平均垂直距离分别为223mm、0mm、-222.5mm和-448mm。具体的机器人位置精度实验数据如表4所示。

实验结果表明，传递机器人在桁杆传递的过程中，其关节运动平稳，并且桁杆传递无明显的晃动，但与理论值相比具有一定的位置偏差。其偏差主要由机械抓取手抓取桁杆位置的变化所造成的，由表4可知，理论上与实验中最大偏差量为2.5mm，最大误差为1.1%。由于机械抓取手抓取部分的设计结构，偏差在允许的范围内仍能稳定的抓取桁杆，因此，实验表明机器人具有一定的位置精度，可以满足桁杆传递的工作条件。

3.3 机器人关节转动实验

机器人关节的转动是桁杆输送和组装过程中必不可少的运动，决定着桁杆的位置与组装时的状态。为了验证桁架组装的过程中机器人关节弯曲和旋转状态下具有较高的灵活性，需要对机器人进行关节转动实验。

机器人转动实验分为3个部分，一是机器人180°摆转关节单独转动实验;二是360°旋转关节单独转动实验;三是180°摆转关节和360°旋转关节协同转动实验。由于机器人位置精度实验是以180°摆转关节单独转动为基础的，因此，机器人关节转动实验只需做二、三种情况状态下的实验即可。

如图14、15所示，分别为机器人的360°旋转关节做单独转动和180°摆转关节与360°旋转关节做协同转动运动时，3种典型位置上桁杆径向中心点与桁架径向中心点的理论距离。通过理论计算可知，当360°旋转关节做30°、60°、90°的单独旋转时，桁杆径向中心点与桁架径向中心点的水平距离分别为225、390、450mm;当180°摆转关节和360°旋转关节均协同转动45°、90°、135°时，桁杆径向中心点与桁架径向中心点的垂直距离分别为875、1300、875mm。

如图16、17所示，在实验中，经过多次测量桁杆径向中心位置与理论值的实际偏移量，通过计算获得360°旋转关节分别做30°、60°、90°的单独转动时，桁杆径向中心点与桁架径向中心点的平均垂直距离分别为223、387.5、447mm;当180°摆转关节和360°旋转关节协同转动时，测得其关节做45°、90°、135°转动的桁杆径向中心点与桁架径向中心点的平均垂直距离分别为872.5、1298、872.5mm。

在实验过程中，无论是关节单独转动还是协同转动，传递的桁杆运动平稳，无明显的晃动。实验值与理论值相比虽然具有一定的偏差，但是实验中最大偏差量为3mm，最大误差为0.89%。误差在关节转动允许的范围内，由此可知，机器人关节的转动只调整桁杆的位置，且对桁杆的位置精度影响较小，具有较高的灵活性。

3.4 机器人桁杆装配实验

桁杆装配是机器人桁架组装的重要环节，机器人的桁杆装配运动直接影响着桁杆在指定位置的组装精度。为了验证桁杆能否到达指定位置完成桁架的组装工作，以组装机器人为研究对象，对机器人进行桁杆装配实验。

桁杆装配实验的组装机器人构型由9个细胞单元模块组成，包括两个旋转组织，一个摆转组织，一个夹爪组织和一个夹爪功能模块。机器人在桁桿传递的过程中，具有一定的位置精度和较高的灵活性。理论上，在桁杆装配时，组装机器人能够满足桁杆装配的精度要求。

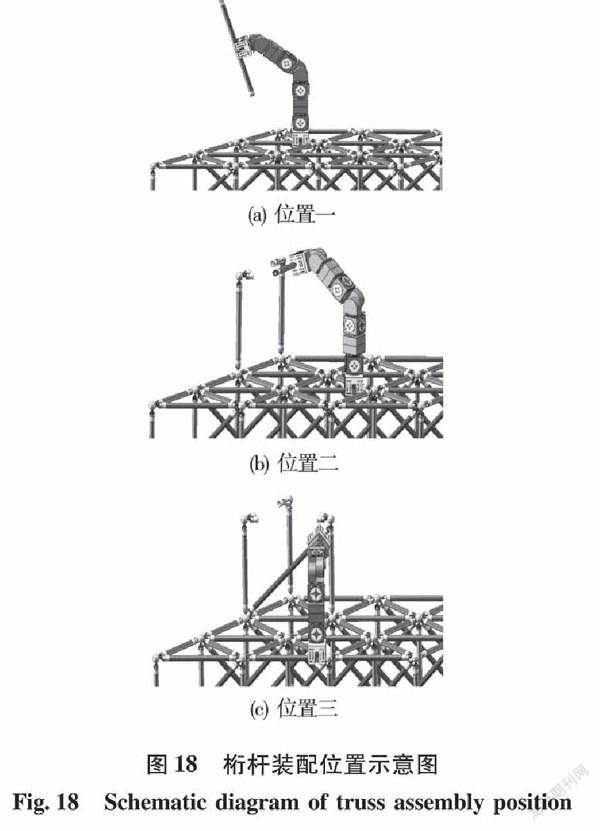
如图18、19所示，分别为桁杆装配的位置示意图和桁杆装配的实验图。在实验的过程中，机器人主要进行桁杆的竖向装配、横向装配和斜向

装配3种位置的桁架组装工作。

实验表明，机器人在进行3种不同位置下的桁架装配工作时，由于桁架球头接口的特殊结构具有一定的导向作用，因此在4mm的误差允许范围内，桁杆都能准确的到达指定的球头装配口中进行装配，并顺利的完成桁架的组装工作。在实验过程中，机器人抓取的桁杆与球头装配孔接触时虽然有轻微晃动，但是对桁架组装的影响较小，符合其运动规律。

4 结 论

本文针对空间桁架的在轨组装任务，创新设计了模块化空间桁架在轨组装机器人的多种异类细胞单元模块，通过运动仿真和机器人桁架组装的实验平台，对机器人进行了运动学分析，验证了机器人运动性能的可靠性与桁架组装的准确性。

1）针对空间桁架的在轨组装任务，对机器人细胞单元模块进行创新设计，为机器人相关在轨工作的构型生成提供基本技术支撑。

2）完成了空间桁架在轨组装机器人的运动学仿真分析，仿真结果表明符合其运动规律。

3）通过搭建桁架组装实验平台，进行了机器人的位置精度、关节转动精度和桁杆装配精度的测量实验，实验结果表明机器人能够准确的完成不同位置的桁架组装任务。

参 考 文 献：

[1] 卢伟， 耿云海， 陈雪芹， 等. 在轨服务航天器对目标的相对位置和姿态耦合控制[J]. 航空学报， 2011， 32（5）： 857.

LU Wei， GENG Yunhai， CHEN Xueqin， et al. Coupling Control of the Relative Position and Attitude of the Target by the In-orbit Service Spacecraft[J]. Acta Aeronautica et Astronautica Sinica， 2011，32（5）： 857.

[2] 赵航， 赵阳， 田浩， 等. 空间细胞机器人系统关键技术及其应用[J]. 宇航学报， 2018， 39（10）： 1071.

ZHAO Hang， ZHAO Yang， TIAN Hao， et al. Key Technology and Application of Space Cell Robot System[J]. Acta Astronautica， 2018， 39（10）： 1071.

[3] 蔡远文， 郭会， 李岩. 航天器在轨组装技术进展[J]. 兵工自动化， 2009， 28 （10）： 6.

CAI Yuanwen， GUO Hui， LI Yan. Progress of Spacecraft On-orbit Assembly Technology[J]. Ordnance Automation， 2009， 28（10）： 6.

[4] 徐国栋， 赵丹， 向文豪， 等. 可重构的卫星/运载复用电子系统设计[J]. 航空学报， 2009， 30（7）： 1298.

XV Guodong， ZHAO Dan， XIANG Wenhao， et al. Design of Reconfigurable Satellite/Carrier Multiplexed Electronic Systems[J]. Acta Aeronautica et Astronautica Sinica， 2009，30（7）： 1298.

[5] 周建平. 我国空间站工程总体构想[J]. 载人航天， 2013， 19（2）： 1.

ZHOU Jianping. General Conception of China′s Space Station Project[J]. Manned Space， 2013， 19（2）： 1.

[6] 刘明尧， 谈大龙， 李斌. 可重构模块化机器人现状和发展[J]. 机器人， 2001（3）： 275.

LIU Mingyao， TAN Dalong， LI Bin. Current Situation and Development of Reconfigurable Modular Robot[J]. The Robot， 2001（3）： 275.

[7] JIA J， JIA Y M， SUN S H. Preliminary Design and Development of an Active Suspension Gravity Compensation System for Ground Verification[J]. Mechanism and Machine Theory， 2018， 128： 492.

[8] 王博， 叶东， 孙兆伟， 等. 模块化可重构卫星在轨自重构的分层规划[J]. 航空学报， 2019， 40（9）： 276.

WANG Bo， YE Dong， SUN Zhaowei， et al. Hierarchical Planning for On-orbit Self-reconstruction of Modular Reconstructible Satellite[J]. Acta Aeronautica et Astronautica Sinica， 2019， 128： 492.

[9] 郑羿. 具有肢体作业功能的多足机器人设计与运动分析[D]. 合肥： 合肥工业大学， 2016： 2.

[10]白鹏. 可重构模块化机器人构形综合与寻优[D]. 沈阳： 东北大学， 2009： 1.

[11]李团结， 张琰， 李涛. 周边桁架可展天线展开过程动力学分析及控制[J]. 航空学报， 2009， 30（3）： 66.

LI Tuanjie， ZHANG Yan， LI Tao. Dynamic Analysis and Control of Deployment Process of Perimeter Truss Deployable Antenna[J]. Acta Aeronautica et Astronautica Sinica， 2009， 30（3）： 66.

[12]常海涛， 黄攀峰， 王明， 等. 空间细胞机器人接管控制的分布式控制分配[J]. 航空学报， 2016， 37（9）： 2864.

CHANG Haitao， HUANG Panfeng， WANG Ming， et al. Distributed Control Allocation for Takeover Control of Space Cell Robot[J]. Acta Aeronautica et Astronautica Sinica， 2016， 37（9）： 2864.

[13]FUKUDA T. Approach to the Dynamically Reconfigurable Robotic System[J]. Journal of Intelligent and Robotic Systems， 1998， 1 （1）： 55.

[14]FUKUDA T， NAKAGAWA S， KAWAUCHI Y， et al. Self Organizing Robots Based on Cell Structures-CKBOT[C]∥IEEE International Workshop on Intelligent Robots.Piscataway， NJ： IEEE Press， 1988.

[15]翟迎新， 让光林. 有限状态多期模型下的最小K熵等价鞅测度期权定价[J]. 武汉科技大学学报， 2016， 39（6）： 472.

ZHAI Yingxin， RANG Guanglin. Option Pricing with Minimum K-Entropy Equivalent Martingale Measure in Finite State Multiphase Model[J]. Journal of Wuhan University of Science and Technology， 2016， 39（6）： 472.

[16]朱杰， 孙毅中， 李吉龙. 面向属性空间分布特征的空间聚类[J]. 遥感学报， 2017， 21（6）： 917.

ZHU Jie， SUN Yizhong， LI Jilong. Spatial Clustering Based on Spatial Distribution Feature of Attribute[J]. Journal of remote sensing， 2017， 21（6）： 917.

[17]HOU F， SHEN W. Graph-based Optimal Reconfiguration Planning for Self-reconfigurable Robots[J]. Robotics and Autonomous Systems， 2014， 62（7）： 1047.

[18]张月， 葛为民， 王肖锋， 等. 自重构机器人的拓扑描述和重构策略研究[J]. 机械设计与制造， 2015（3）： 177.

ZHANG Yue， GE Weimin， WANG Xiaofeng， et al. Topology Description and Reconstruction Strategy of Self-reconfigurable Robot[J]. Mechanical Design and Manufacture， 2015（3）： 177.

[19]刘振民. 可重构机器人动力学自动建模及轨迹规划研究[D]. 天津： 天津理工大学， 2015： 12.

[20]夏振兴. 模块化自重构机器人结构设计及自变形方法的研究[D]. 上海： 上海交通大学， 2007： 5.

[21]费燕琼， 张鑫， 夏振兴. 自重构模块化机器人的运动空间及自变形算法[J]. 机械工程学报， 2009， 45（3）：197.

FEI Yanqiong， ZHANG Xin， XIA Zhenxing. Motion Space and Self-deformation Algorithm of Self-reconfigurable Modular Robot[J]. Chinese Journal of Mechanical Engineering， 2009， 45（3）： 197.

[22]ZYKOV V， MYTILINAIOS E， DESNOYER M， et al. Evolved and Designed Self-reproducing Modular Robotics[J]. IEEE Transactions on Robotics， 2007， 23（2）： 308.

（編辑：王 萍）

收稿日期： 2020-10-07

基金项目： 国家自然科学基金（52075134）;黑龙江省自然科学基金（LH2019E062）;黑龙江省普通高校基本科研业务费专项资金项目（LGYC2018JC040）; 黑龙江省普通本科高等学校青年创新人才培养计划项目（UNPYSCT-2017077）.

作者简介：

吕晶薇（1986—），女，硕士;

高语斐（1997—），女，硕士研究生.

通信作者：

戴 野（1982—），男，博士，副教授，E-mail：daiye312@163.com.

3484501908270