表面微结构参数对轴承钢球展开轮磨损量的影响
2021-03-14潘承怡曹冠群童圆栖常佳豪
潘承怡 曹冠群 童圆栖 常佳豪





摘 要:为研究轴承钢球展开轮表面微结构主要参数(面积、形状、深度)对干摩擦条件下展开轮磨损量的影响,采用正交试验法对不同参数的微结构表面进行试验,应用仿真软件进行应力分析,得到不同几何参数微结构的微观应力分布状态,结合试验与应力分析的结果对Archard磨损模型进行修正。结果表明:减磨效果最好的是菱形微结构,单坑面积为3.14×10-2 mm2,深度為150 μm。发现不同几何参数微结构的高应力区分布位置,推导出包含微结构主要参数变量的磨损量计算模型,可为微结构展开轮的设计及寿命预测提供理论依据。
关键词:表面微结构参数;轴承钢球展开轮;正交实验法;应力仿真;磨损模型
DOI:10.15938/j.jhust.2021.06.006
中图分类号: TH117.1
文献标志码: A
文章编号: 1007-2683(2021)06-0040-07
Influence of Surface Microstructure Parameters
on Wear of Bearing Steel Ball Unfolding Wheel
PAN Cheng-yi, CAO Guan-qun, TONG Yuan-qi, CHANG Jia-hao
(School of Mechanical and Power Engineering, Harbin University of Science and Technology, Harbin 150080,China)
Abstract:In order to study the dry friction wear relationship between the bearing steel ball unfolding wheel with the surface microstructure parameters (area, shape and depth), the orthogonal test method was used to test the microstructure with different parameters. The simulation software was used to analyze the stress. The stress distribution of the microstructure with different parameters is obtained. The Archard wear model was modified by combining the results of tests and stress analysis. The results show that the microstructural parameters with the best wear reduction effect in the experimental range were the diamond microstructures with an area of 3.14×10-2 mm2 and a depth of 150 μm. The distribution locations of high stress zones in microstructures with different geometric parameters are found. The wear calculation model containing the parameters of the microstructure is derived. It can provide theoretical basis for the design and life prediction of the microstructure unfolding wheel.
Keywords:surface microstructure parameter; bearing steel ball unfolding wheel; orthogonal test; stress analyze; wear model
0 引 言
钢球作为轴承滚动体,对轴承的性能起着决定性作用[1]。在钢球制造过程中,钢球表面不可避免地会产生一定的损伤和缺陷。这些损伤和缺陷会影响轴承的运行甚至导致轴承损坏。因此,检测钢球表面质量非常重要[2-3]。轴承钢球展开轮是钢球表面缺陷自动检测机构的关键部件,钢球与展开轮之间的摩擦力使钢球实现了全表面展开运动[4]。摩擦引起的展开轮磨损将影响检钢球测精度和效率,进而导致展开轮失效[5-6],因此,需要提高展开轮表面的耐磨性。
近年来,模仿生物体表面的微结构,在金属零件表面加工凹坑、凸起或条纹等来提高耐磨性已被证明非常有效,许多学者基于仿生摩擦学研究了提高摩擦副表面摩擦磨损特性的方法[7-10]。缪晨炜等[11]发现同种织构应用于不同材料表面摩擦副的性能会呈现差异性。牛一旭等[12]发现载荷对织构表面摩擦性能影响较大。苏峰华等[13]发现织构深度能显著影响油润滑条件下的不锈钢表面的摩擦磨损性能。Jeyaprakash等[14]验证了激光加工提高了工件表面硬度和耐磨性。佟欣等[15]对硬质合金微结构材料的耐磨性机理及性能进行了实验和仿真分析。万泉[16]与杨树才等[17]分别对刀具微观结构参数优化进行了研究。赵彦玲等[18]对展开轮表面微结构的摩擦磨损特性进行了初步研究,但对微结构参数与磨损特性的影响机理缺乏深入分析。
根据研究表明,凹坑微结构应用于展开轮工作表面,可减少其磨损,并提高使用寿命。本文采用激光技术在盘形试件表面加工不同参数(形状、面积和深度)的凹坑形微结构,建立正交实验和应力仿真分析,研究微结构参数对磨损量的影响,并推导微结构表面的磨损量计算模型,为后续进行微结构展开轮的设计和磨损寿命预测提供理论依据。
1 实 验
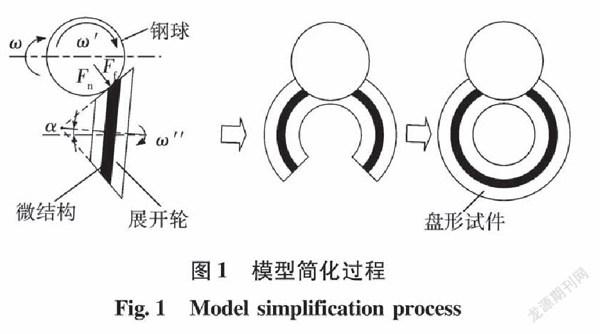
如图1所示,轴承钢球展开轮的工作表面由两个偏置锥面组成,两锥面轴线与展开轮轴线处于同一平面且呈反向交角α,一般为1°[4]。工作时,钢球受外力驱动以角速度ω绕y轴转动,在图示平面内,钢球受到展开轮上两锥面产生的法向力Fn与切向摩擦力Ff。当展开轮处于图示位置时,切向摩擦力Ff驱动钢球以角速度ω′顺时针旋转。当展开轮旋转180°后,摩擦力Ff方向变为相反方向,将驱动钢球逆时针方向旋转。展开轮以角速度ω″绕其轴线回转。这种机构使钢球在检测过程中得到全表面展开[5]。
工作过程中,钢球在图示平面内的侧向转动产生其与展开轮锥面间的滑动干摩擦,容易导致展开轮工作面因磨损而失效。为减轻磨损,将凹坑微结构应用于展开轮双锥面与钢球的接触区。由于展开轮结构的特殊性,实验样件较难保证加工精度,并且为消除锥轮尺寸对磨损的影响,使磨损实验更具普遍适用性,现对展开轮表面进行作曲面展开,并补全为一平环面,如图1所示。用钢球与平面接触代替钢球与锥面的接触,用圆柱体代替圆锥体,使磨损实验和模拟仿真得到简化。
1.1 实验方案
为了研究展开轮的磨损特性,预测展开轮的寿命,估计其剩余寿命,需要通过实验来测量磨损量。如图2(a)所示为表面加工有凹坑微结构的盘形试件。采用激光烧蚀方法在试件表面加工不同形状和尺寸的微结构凹坑,如图2(b)所示为试件上表面不同微结构形状示的意图,有圆形、方形和菱形。该试件由Cr1Mo2W50制成,与展开轮的材料相同,其内径、外径和高度分别为,Φ28mm、Φ54mm和Φ18mm。钢球由GCr15钢制成,直径为Φ28mm。如图3所示为搭建的实验台。
采用正交实验设计方法,以形状(圆形、方形、菱形)、面积(7.85×10-3mm2、1.76×10-2mm2、3.14×10-2mm2)和深度(50μm、100μm、150μm)作为实验因素,针对磨损量进行正交实验。激光加工的微结构在VHX-1000超景深显微镜下的形貌如图4所示。实验负荷设定为2N,磨损时间设定为5h。试件转速为1500r/min。磨损量采用BSM220.4精密电子天平称重测定。
1.2 实验结果
通过磨损实验测得不同各种试件的磨损量,并将实验结果列于计算表,如表1所示。
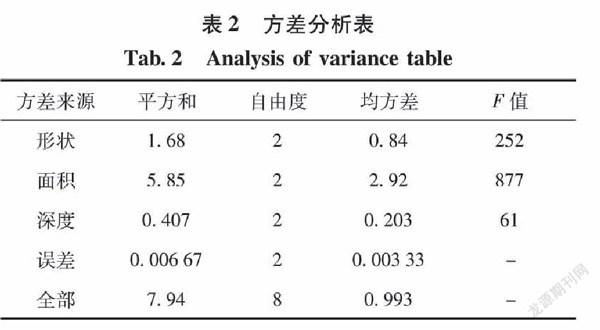
采用方差分析法对实验结果进行处理,处理结果如表2所示。
根据显著性水平α=0.95查得相应分位数值F0.95(2,2)=19.00,由此判断形状、面积、深度均对磨损量有较大影响,影响显著性依次为:面积>形状>深度。磨损量最小的微结构方案为:形状为菱形,面积为3.14×10-2mm2,深度为150μm,以此方案加工试件并实验,测得磨损量为2.1mg与分析结果相符。
2 仿真分析
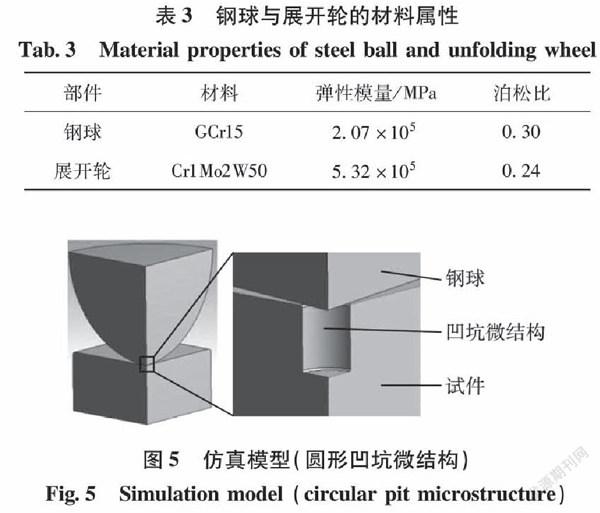
为进一步研究微结构的磨损机理,考虑到表面接触的耐久性,需要对其表层和次表层应力进行分析。参照上述实验建立模型并使用ANSYS软件进行应力仿真分析。输入表3中的材料属性并建立钢球与微结构表面单个微凹坑接触的模型,根据赫兹理论计算钢球与无微结构展开轮接触区长轴长度为109.8μm,考虑到试件上微结构凹坑间距统一为400μm,大于试件与钢球接触区域直径的3倍,单个凹坑接触时,其余凹坑对应力分布影响可以忽略。为分析方便,接触模型设置为单个微凹坑接触,取轴截面的1/4显示,如图5所示。
2.1 面积对磨损量的影响
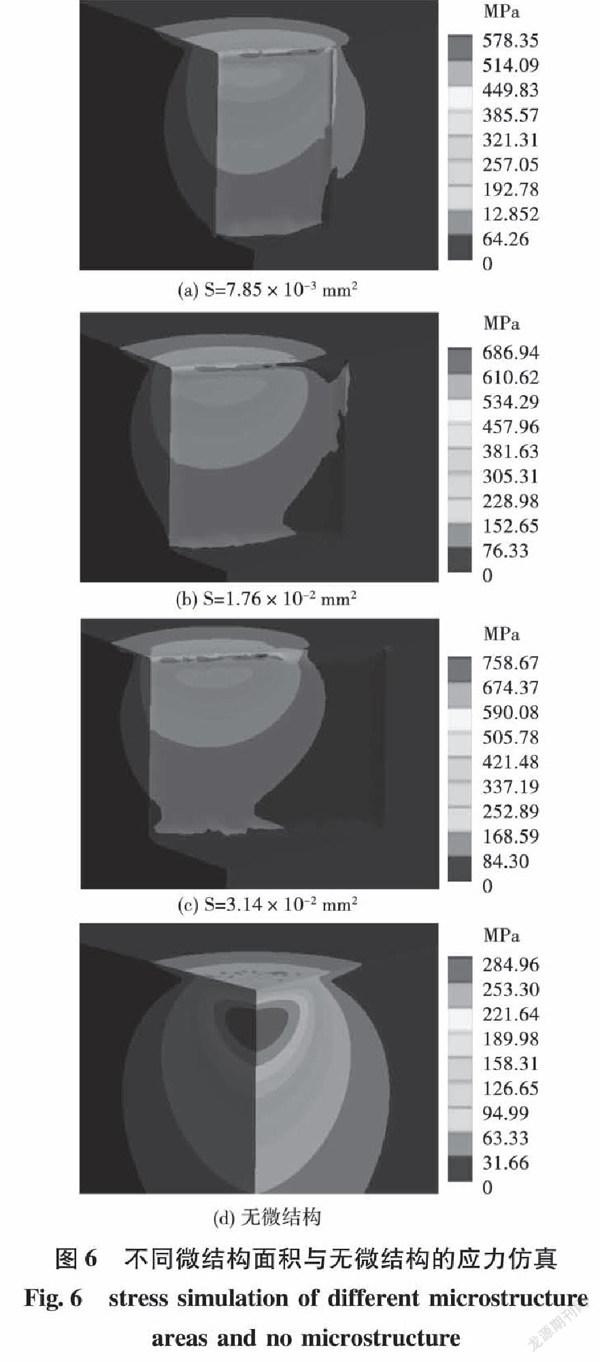
为研究凹坑面积对磨损量的影响,选择实验最优的深度为150μm的菱形凹坑,形成的微结构面积分别为7.85×10-3mm2、1.76×10-2mm2、3.14×10-2mm2,3种大小面积的微结构表面与钢球接触的应力仿真与无微结构表面的应力仿真进行对比,如图6所示。
由图6可见,微结构面积越大,高应力区越小,越容易处于激光加工过程中形成的硬化区之内[18]。虽然微结构面积越大,最大应力越大,但是高应力区分布在微结构凹坑周围,处于硬化区内,所以减小了产生裂纹和碎屑的可能。而与无微结构的情况下,虽然最大应力更小,但是高应力区明显位于比较深的次表层,而且高应力区范围比较大,不像有微结构时最大应力位置更靠近试件表面。所以,在较深的大范围的次表面应力作用下,无微结构的光滑表面在材料无激光硬化区的情况下,容易形成大的金属屑剥落,即形成较大磨粒,加剧磨损。另外,还考虑到磨屑在微结构凹坑中的储存功能[15~16],可以得到以下推论:
1)钢球在试件表面滚动时,试件微观上从最大应力点开始破坏,产生磨损。微结构试件的最大应力点比非微结构试件更靠近接触面。含有微结构的试件在磨损过程中产生的磨屑直径比无微结构小得多,因此磨屑形成后很容易掉入,即被凹坑所捕获,进一步降低了磨粒磨损,从而降低了磨损量,起到了减磨耐磨的作用。
2)由于微结构凹坑与钢球接触,随着微结构面积的增大,高应力区逐渐缩小至微结构硬化边缘,微结构凹坑周围的高应力区体积逐渐减小。众所周知,在相同的条件下,磨损与硬度成反比。因此,微结构试件的磨损量由于激光产生的凹坑硬化区域而降低。
2.2 形状对磨损量的影响
为研究形狀对磨损量的影响,选择实验最优的深度为150μm,面积为3.14×10-2mm2的三种形状(圆形、正方形、菱形)的微结构表面与钢球接触进行应力仿真。圆形和正方形微结构的仿真结果如图7所示。
比较图7和图6(c)可以看出,菱形微结构的最大应力最小,为758.67MPa。方形微结构的最大应力最大为774.48MPa。圆形微结构应力最大,为860.08MPa。高应力区的体积随最大应力增大而减小,但不明显。可以得到以下推论:
在相同的微结构凹坑面积下,不同形状的微结构,其高应力区体积接近,而应力峰值不同。菱形微结构的应力峰值最小,耐磨性最佳;方形微结构应力峰值比菱形稍大,耐磨性中等;圆形微结构应力峰值最大,耐磨性相对较差。
2.3 深度对磨损量的影响
为研究深度对磨损量的影响,选择实验最优的菱形凹坑、面积为3.14×10-2mm2的不同深度(50μm、100μm、150μm)的微结构进行应力仿真,考虑到深度变化可能存在边际递减效应,因此增加深度为200μm的仿真模型。50μm、100μm与200μm深度微结构的应力仿真结果如图8所示。
比较图8和图6(c)可以看出,当凹坑微结构深度较浅时(50μm),最大应力稍大(780.92MPa),并且会在凹坑底部形成第二个应力集中区,并因此会导致磨损的加剧。当凹坑深度为100μm、 150μm、200μm时,最大应力分别为762.66MPa、758.67MPa、757.38MPa,可见当凹坑足够深时(100μm以上),其最大应力及应力分布变化都较小。结合实验数据可得到以下推论:
当凹坑微结构深度不足时,凹坑底部形成第二个应力集中区,微结构减磨性受到影响;随着凹坑深度的逐渐增加,在凹坑底部的应力集中现象逐渐减小,微结构减磨性提高;当凹坑深度达到某一临界值时第二应力集中区消失,此时如继续增加凹坑深度对磨损量的减少并无明显作用。
2.4 高应力区对磨损量的影响
为进一步分析比较,按照与干摩擦正交实验相同的9种微结构参数进行表面接触应力仿真,仿真得到的最大应力与实验得到的磨损量对应关系如图9所示。从图中可以看出,微结构试件的磨损量与最大应力呈较明显的反比关系。在相同负载条件下,最大应力越大代表着应力集中程度越高,高应力区体积越小,即高应力区体积与最大应力成反比,因此,磨损量与高应力区体积成正比。这与上述微结构参数(面积、形状、深度)通过影响高应力区体积而影响磨损量的推论是相一致的。
综上所述,不同的微结构参数将影响试件的应力分布,进而影响高应力区的体积,从而影响磨损量。影响程度最大的是微坑的面积,其次是形状,再次是深度。
3 磨损模型
磨损的常用模型为Archard磨损模型[18-20],其形式为
V=KLPH(1)
式中:V为磨损体积;K为磨损系数,近似于磨粒产生的概率;L为磨损的距离;P为载荷;H为较软的材料硬度。
磨损距离L可以表示为接触点处的相对速度v与时间t的乘积,即
L=vt(2)
将式(2)代入式(1)并将等式两侧乘以材料密度ρ得到磨损质量的表达式:
W=ρKvtPH(3)
考虑到加工硬化作用,其硬度H发生改变且不易测量,将磨损系数与硬度比K/H记为K1,将上式变形后得到表达式
K1=K/H(4)
W=ρK1vtP(5)
考虑到钢球与带有微结构试件的表面接触应力分布发生变化,将导致K1发生变化,因此采用微结构面积S、形状系数A(A为过微结构几何中心的最长轴与最短轴之比)、深度h对K1进行修正。
考虑微结构加工后其表面材料硬度H为定值,因此已确定微结构参数的展开轮磨粒产生的概率K与K1成正比。且磨粒产生的概率K与高应力区的体积V、最大应力σ成正比,在一定范围内随深度h增加而增加,超出此范围时深度增加影响逐渐降低,当深度为0时,K1应与无微结构试件实验测得的K/H相同,因而假设K1符合如下关系式:
K1=a0Vσln(a1h+1)+K0(6)
式中:a0、a1为未知常量;K0为无微结构试件实验测得的K/H值。
根据仿真结果,可得到高应力区的体积V主要与微结构面积S(单位mm2)和深度h(单位μm)有关,最大应力σ同时与微结构面积S、形状系数A(无量纲)相关,设其关系为非线性关系,即
V=a2Sa3ha4
σ=a5Sa6Aa7 (7)
式中:a2、a3、a4、a5、a6、a7均为未知常量。
将式(7)代入式(6),合并常数项,得到K1的修正表達式:
K1=b0Sb1Ab2hb3ln(b4h+1)+K0(8)
将实验数据代入式(5),得到实验时不同微结构的K1值,列于表4,并按照式(8)采用最小二乘法拟合解出未知常量b0、b1、b2、b3、b4,从而得到磨损系数与微结构参数的关系:
K1=2.307×10-5-0.01597S0.08237A0.1099h-0.9234ln(1.213×10-3h+1)(9)
其拟合优度R2=0.99,证明实验数据与实验模型较好吻合。
将K1代入式(5),整理后得凹坑微结构展开轮磨损量的计算公式为
W=ρvtP(2.307×10-5-0.01597S0.08237A0.1099h-0.9234ln(1.213×10-3h+1))(10)
将实验数据代入式(10)得到各实验的计算磨损量,与实验磨损量进行对比,如图11所示。计算结果与实验结果误差较小,最大误差率小于5.0%,因而可以根据式(10)对凹坑微结构展开轮的磨损量进行计算。
4 结 论
1)为了减少钢球摩擦引起的展开轮表面磨损,采用正交实验方法研究了微结构面积、形状和深度对磨损的影响。微结构为菱形、面积为3.14×10-2mm2、深度为150μm时具备较好的抗磨效果。影响显著性依次为面积、形状、深度。
2)通过应力仿真分析,发现不同的微结构参数通过改变应力分布状态影响高应力区体积是影响磨损量的根本原因。凹坑面积增大磨损量减小,菱形凹坑优于圆形和正方形,微结构深度需达到100μm以上才能达到较好减磨效果。
3)修正了Achard磨损模型,得到了含有微结构参数(形状系数A、面积S、深度h)影响因素的磨损量计算数学表达式,其计算结果与实验数据的最大误差率小于5%,为具有微结构表面的展开轮设计提供了理论依据。
參 考 文 献:
[1] ZHANG Kai, FU Luhua, WANG Zhong, et al. Research on Surface Defect Detection of Ceramic Ball Based on Fringe Reflection[J]. Optical Engineering, 2017, 56(10): 104104.1.
[2] ZHANG Huayu, MA Longyu, XIE Fengqin. A Method of Steel Ball Surface Quality Inspection Based on Flexible Arrayed Dddy Current Sensor[J]. Measurement: Journal of the International Measurement Confederation, 2019, 144:192.
[3] ZHANG Huayu, XIE Fengqin, CAO Maoyong, et al. A Steel Ball Surface Quality Inspection Method Based on a Circumferential Eddy Current Array Sensor[J]. Sensors, 2017,17:1536.
[4] 赵彦玲, 赵志强, 鲍玉冬, 等. 钢球全表面展开原理及方法[J]. 机械工程学报, 2016, 52(17): 205.
ZHAO Yanling, ZHAO Zhiqiang, BAO Yudong, et al. The Principle and Method of Unfolding the Whole Surface of Steel Ball[J]. Journal of Mechanical Engineering, 2016, 52(17): 205.
[5] ZHAO Yanling, XIA Chengtao, WANG Hongbo,et al. Analysis and Numerical Simulation of Rolling Contact Between Sphere and Cone[J], Chinese Journal of Mechanical Engineering (English Edition), 2015, 28(3): 521.
[6] PAN Chengyi, LI Xia, WANG Hepeng, et al. Wear Numerical Simulation and Life Prediction of Microstructure Surface Unfolding Wheel for Steel Ball Inspection[J]. Mechanisms and Machine Science, 2020,77: 518.
[7] FANG Shiqi, KLEIN S, HSU Chiajui, et al. Fabrication and Tribological Performance of a Laser-textured Hardmetal Guiding Stone for Honing Processes[J]. International Journal of Refractory Metals & Hard Materials, 2019, 84: 105034.1.
[8] LU Ping, WOOD RJK, GEE MG, et al. The Use of Anisotropic Texturing for Control of Directional Friction[J]. Tribology International, 2017, 113:169.
[9] YE Shaogang, TANG Hesheng, REN Yan, et al. Study on the Load-carrying Capacity of Surface Textured Slipper Bearing of Axial Piston Pump[J]. Applied Mathematical Modelling,2019,77:554.
[10]DING Liang, DRAGOS Axinte, PAUL Butler-Smith, et al. Study on the Characterisation of the PTFE Transfer Film and the Dimensional Designing of Surface Texturing in a Dry-lubricated Bearing System[J]. WEAR, 2020(448/449): 1.
[11]ZHAN Xinhua, YI Peng, LIU Yancong, et al. Effects of Single- and Multi-shape Laser-textured Surfaces on Tribological Properties under Dry Friction[J]. Proceedings of the Institution of Mechanical Engineers Part C-journal of Mechanical Engineering Science,2019,234(7):1382.
[12]CHEN Ping, LI Junling, LI Yunlong. Effect of Geometric Micro-groove Texture Patterns on Tribological Performance of Stainless Steel[J]. Journal of Central South University, 2018, 25(2): 331.
[13]苏峰华,毛川,李助军. 织构深度对不锈钢表面油润滑条件下摩擦学性能影响的试验和仿真研究[J]. 摩擦学学报, 2019,39(2):181.
SU Fenghua, MAO Chuan, LI Zhujun. Experiment and Simulation Study on the Effect of Texture Depth on Tribological Properties of Stainless Steel Surface under Oil Lubricating Condition[J]. Tribology,2019,39(2):181.
[14]JEYAPRAKASH N, YANG Chehua, MUTHUKANNAN Duraiselvam, et al. Investigation of High Temperature Wear Performance on Laser Processed Nodular Iron Using Optimization Technique[J]. Results in Physics,2019,15:102585.
[15]TONG Xin, YANG Shucai, LIU Xianli, et al. Friction, Wear, and Fatigue Analysis for Micro-textured Cemented Carbide[J]. Proceedings of the Institution of Mechanical Engineers Part C-journal of Mechanical Engineering Science, 2019, 233(17): 5989.
[16]WAN Q, ZHENGMl, YANG S C, et al. Optimization of Micro-texture Distribution Through Finite-Element Simulation[J]. International Journal of Simulation Modelling. 2019, 18(3): 543.
[17]杨树财,马旭青,张玉华,等. 球头铣刀最优微织构参数确定方法[J].哈尔滨理工大学学报, 2019, 24(5): 47.
YANG Shucai, MA Xuqing, ZHANG Yuhua, et al. Research on the Method of Determining the Optimum Micro-texture Parameters of Ball-end Mill[J]. Journal of Harbin University of Science and Technology. 2019,24(5):47.
[18]赵彦玲, 耿伟, 鲍玉冬, 等. 钢球检测用展开轮表面微结构增摩降磨特性分析[J]. 摩擦学学报,2017,37(3):348.
ZHAO Yanling, GENG Wei, BAO Yudong, et al. Analysis of Friction and Wear Properties of Microstructure on the Unfolding Wheel Used for Steel Ball Inspection[J]. Tribology, 2017,37(3):348.
[19]ZHANG Zhao, LU Wenzhuang, LIU Wei, et al. Friction-reducing Effect and Damage Mechanism of Laser Micro-texture on Diamond Films During Friction[J]. MODERN PHYSICS LETTERS B, 2019,33(24):1950283.
[20]潘承怡, 李侠, 赵彦玲, 等. 应用数值模拟的钢球检测展开轮磨损寿命预测[J]. 哈尔滨理工大学学报,2020,25(02): 50.
PAN Chengyi, LI Xia, ZHAO Yanling, et al. Wear Life Prediction on Unfolding Wheel of Steel Ball Detection by Using Numerical Simulation[J]. Journal of Harbin University of Science and Technology,2020,25(2):50.
(编辑:王 萍)
收稿日期: 2020-10-30
基金项目: 黑龙江省自然科學基金(E2017052).
作者简介:
曹冠群(1992—),男,硕士研究生;
童圆栖(1994—),女,硕士研究生.
通信作者:
潘承怡(1971—),女,博士,硕士研究生导师,E-mail:panchengyi2010@163.com.
3719501908220
