鲁棒无迹四元数卡尔曼滤波初始对准算法∗

周晓仁徐 祥赵鹤鸣

(苏州大学电子信息学院，江苏 苏州 215006)

捷联惯性导航系统的结果通过航位推算获得，在导航过程之前需要获得载体的位置，速度和姿态的三个初始信息。 通常载体的初始位置和初始速度可以由GPS 获取，而初始姿态需要通过初始对准提供。初始对准有两个的过程:粗对准和精对准。 粗对准提供一个粗略的姿态矩阵，从而精对准才能满足失准角误差模型来对姿态矩阵进行更准确得估计。

为提高粗对准的精度，众多学者提出了改进的算法。 文献[1－2]提出了将姿态矩阵用惯性系分解的方法，减小了基座摇摆带来的影响。 在惯性系对准方法提出之后，产生了众多改进的基于重力视矢量运动的摇摆基座粗对准算法，文献[3－4]提出了参数识别的算法，提高了初始载体系下的矢量的精度，从而提高了粗对准的精度。 文献[5]提出了基于最优化的初始姿态确定方法(optimization-based alignment，OBA)，该方法能够充分利用观测和参考矢量，通过连续定姿的方式加快了粗对准的速度。 文献[6]提出了速度/位置积分公式，使用外部辅助设备GPS 构造观测矢量和参考矢量，通过OBA 法完成动基座初始对准。 文献[7－8]提出了回溯法来缩短初始对准的时间。 但以上的方法并不适用于低精度传感器，因为低精度传感器的陀螺零偏造成的累积误差会造成参考矢量精度的下降，从而导致对准结果不理想。 文献[9－10]采用非线性姿态估计的算法，将陀螺零偏加入预测方程，提高了粗对准的稳定性和精度。 然而，该算法的鲁棒性不足，不能抑制GPS 野值带来的影响。 文献[11]提出了由位置轨迹构造矢量的粗对准方法，该方法虽然在一定程度上能够抑制野值的影响，但是在根本上未去除野值。文献[12]提出了基于矢量重构的鲁棒初始对准方法，但是该方法只能用于惯导系统与多普勒速度仪(doppler velocity log，DVL)组合导航系统。 文献[13]提出了一种基于Huber 的无迹滤波算法，并将其应用于无人机编队飞行中相对位置、速度和姿态的精确估计。 该算法通过改变量测噪声方差矩阵，修改量测更新公式来消除野值的影响，但与本文相比，未能在观测矢量中体现出消除野值的效果。

为解决上述的在低精度传感器初始对准时的两个问题:陀螺零偏和GPS 野值影响，本文使用模值匹配法，把规范化模值平方误差作为量测残差，构造了改进的观测矢量， 结合无迹卡尔曼滤波(unscented Kalman filter，UKF)推导了基于四元数的鲁棒无迹卡尔曼滤波算法，在未修改量测更新公式的情况下完成了对载体姿态与陀螺零偏的估计，抑制了陀螺零偏和GPS 野值的影响，提高了初始对准的精度。

1 传统动基座初始对准基本原理

定义i 为初始时刻的地球坐标系且相对于惯性坐标系静止。e为与地球固连的地球坐标系。n为导航坐标系，原点在载体中心，x，y，z三轴分别指向东，北，天方向。b为载体坐标系，原点在载体中心，x，y，z三轴分别指向载体的右，前，上方向。n0为导航惯性坐标系，与初始时刻的n系重合。b0为载体惯性坐标系，与初始时刻的b系重合。 则比力方程可以表示为:

具体的离散形式可以参考文献[8]。 式中，tM＝MΔtg，tk＝kΔtg，Δtg＝tk＋1－tk。 利用离散的观测矢量和参考矢量来构建tM时刻的矩阵KM:

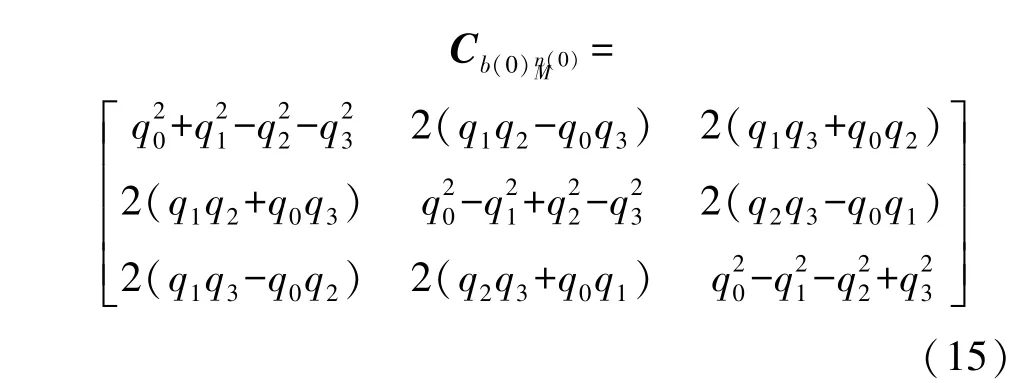
结合式(2)～式(4)可以求解tM时刻的载体的姿态矩阵。

2 无迹四元数卡尔曼滤波模型

2.1 预测模型

2.2 量测模型

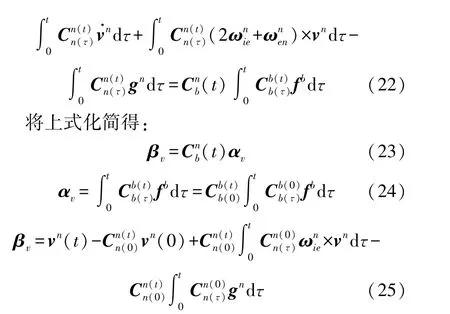
经过离散化:

3 GPS 野值影响与模值匹配权值函数

GPS 接收机容易受到外部环境的影响比如障碍物，多径效应等[11]，输出有时会出现野值，其实际速度测量值与理想值的关系如下式所示:

式中:γ表示高斯阈值，在本文中取γ为2.25。 通过该权值函数可以有效得抑制异常量测对状态估计的影响。

4 鲁棒无迹四元数估计器

将UKF 应用于估计载体的姿态四元数，完成初始对准的方法称为无迹四元数估计器(unscented quaternion estimator，USQUE)。 通常，为了满足运算过程中四元数保持归一化的条件，在USQUE 中采用修正罗德里格参数( modified Rodrigues parameters，MRP)作为状态向量。 本章结合USQUE与权值函数推导了鲁棒无迹四元数估计器(robust unscented quaternion estimator，RUSQUE)。

式中:a为一个取值范围为0 到1 的常数，f是比例因子。 在RUSQUE 中，设状态向量xk＝[δpk；εk]，εk为k时刻的陀螺零偏状态向量。

4.1 状态初始化

设k－1 时刻的状态最优估计向量为＾xk－1，相应的状态协方差矩阵为Pk－1，最优估计四元数为＾qk－1。

（1）全新的课表管理。学生可以通过系统获取自己的课表，查看一起上课的同学的微博，还可以实名或匿名向相关教师提问或建议，也可取代原来的评教方式对教师进行评教。

4.2 预测更新

4.3 量测更新

将预测四元数Sigma 点集代入量测方程(27)得到量测预测的Sigma 点集为:

4.4 姿态更新

5 实验与分析

5.1 仿真实验

为验证本文提出的算法，本节设计了仿真实验。共有5 种算法进行对比。

方案1:OBA 法，GPS 速度含野值。

方案2:RUSQUE 法，GPS 速度含野值。

方案3:USQUE 法，GPS 速度含野值。

方案4:OBA 法，GPS 速度不含野值。

方案5:USQUE 法，GPS 速度不含野值。

表1 传感器误差特性

表2 载体运动信息

设定惯性传感器数据输出频率为200 Hz，GPS数据输出频率为1 Hz，GPS 量测噪声设置:速度为0.1 m/s，位置为1 m。

图1～图4 分别为载体的运动轨迹，真实姿态角，运动速度。 运动速度的噪声在本文中设其分布为:

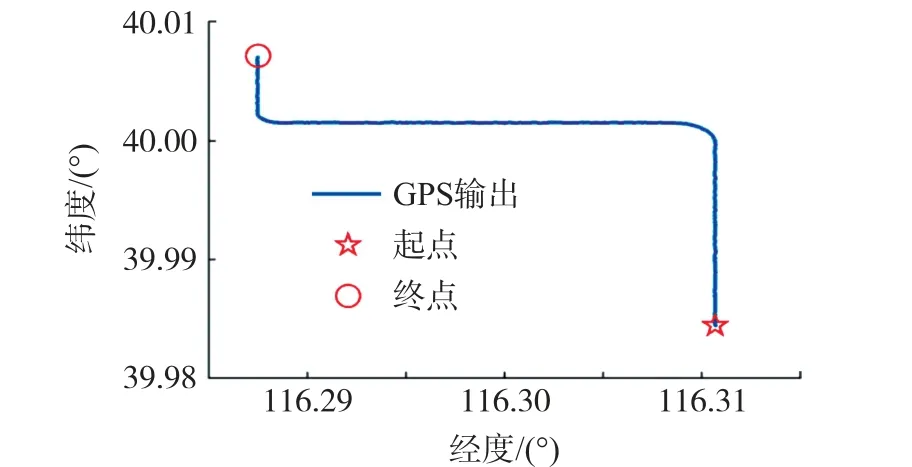
图1 载体的运动轨迹

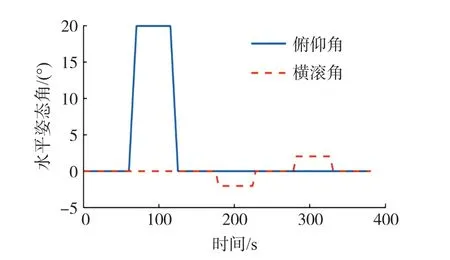
图2 真实水平姿态角

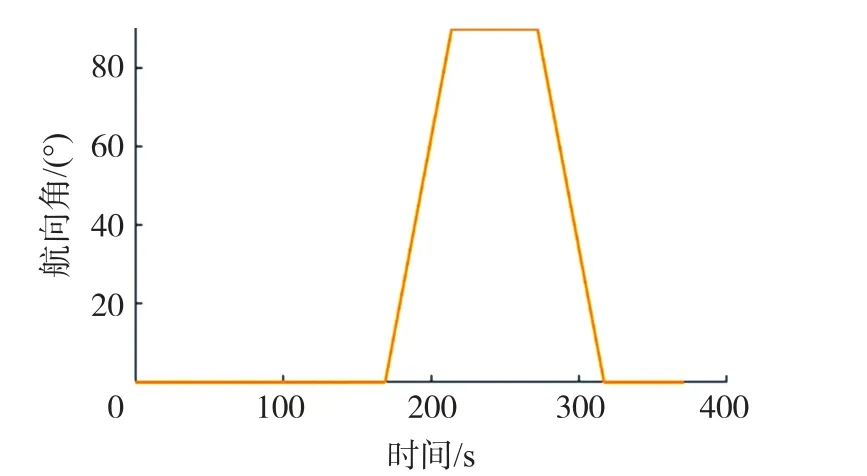
图3 真实航向角

图4 载体运动速度

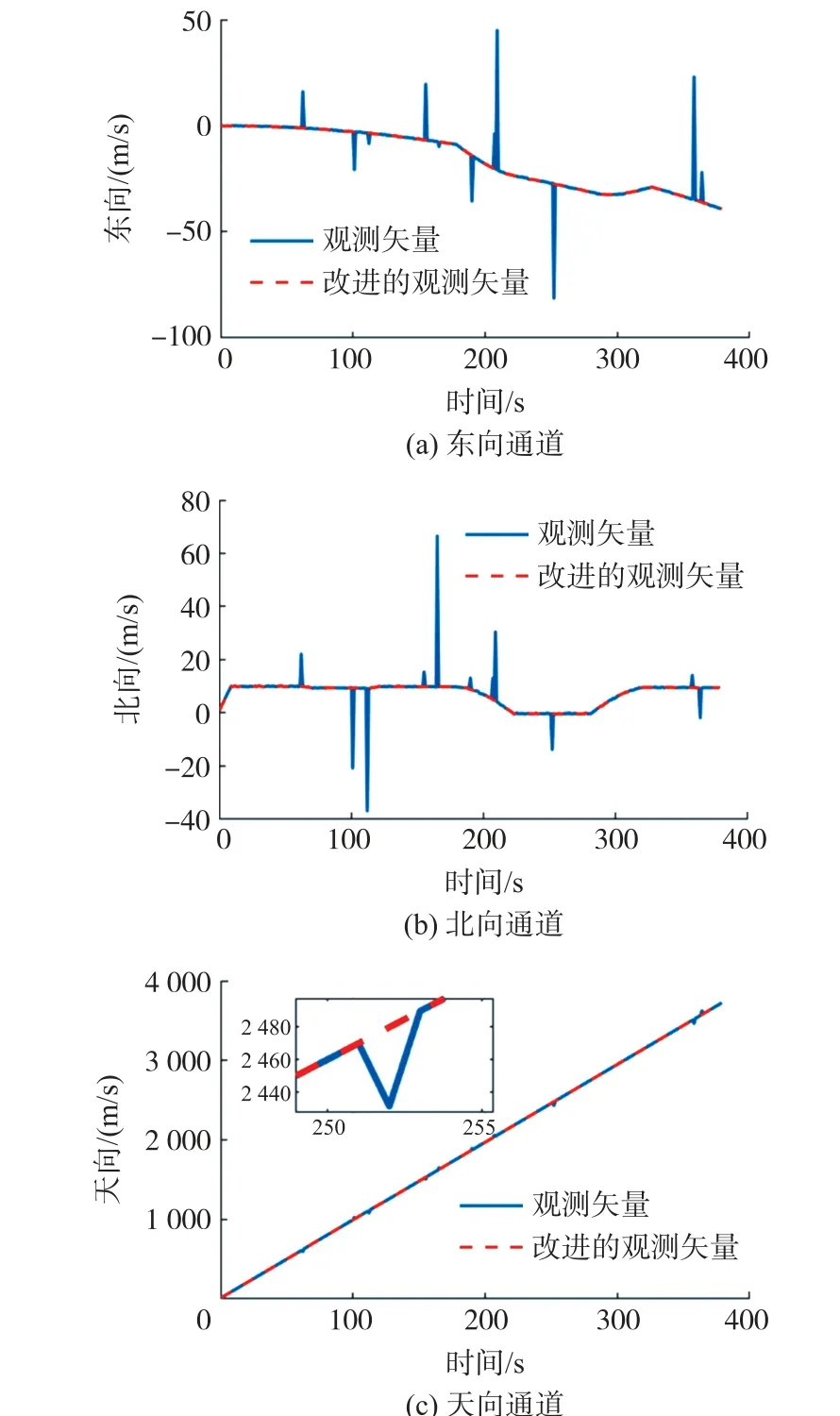
图5 改进前后的观测矢量

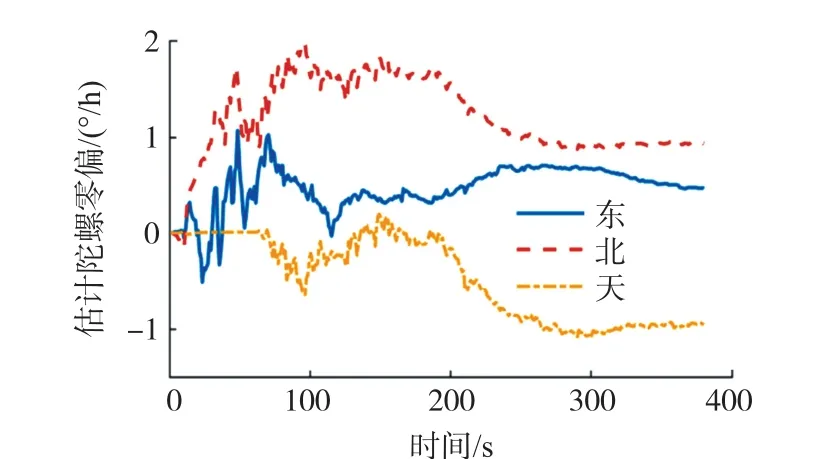
图6 陀螺零偏估计

图7～图9 分别为俯仰角，横滚角，航向角的对准误差曲线图。 当GPS 速度中包含野值时，OBA 法与USQUE 法受到异常观测矢量的影响，导致姿态角误差曲线产生锯齿状的抖动。 RUSQUE 法由于改进的参考矢量有效得去除了野值，对准误差曲线趋于平稳。 当GPS 速度中没有野值时，OBA 法与USQUE 法的航向角误差曲线有着明显的差异，OBA 法由于陀螺仪的零偏造成的累积误差而导致曲线呈现波动特性。 方案2，4 和5 在经过21 s 后，俯仰角误差小于0.1°，横滚角误差小于0.15°。 在航向角方面，281 s～381 s 间三种方案的误差均值分别为－0.713 9°，3.032 0°和－0.684 8°，误差标准差分别为0.015 7°，0.659 2°和0.014 4°。 仿真实验验证了RUSQUE 法的鲁棒性以及对于陀螺零偏抑制的有效性。

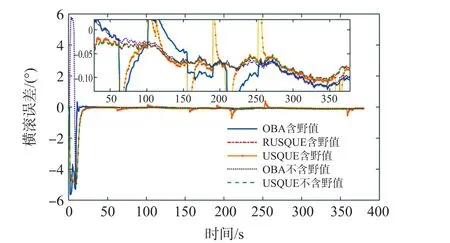
图7 俯仰角误差

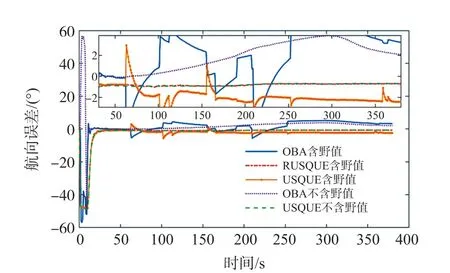
图8 横滚角误差

图9 航向角误差

5.2 跑车实验

本节设计了跑车实验来进一步验证本文提出的算法。 车载导航设备如图10 所示。 跑车实验过程中使用自制的微型惯性测量单元(miniature inertial measurement unit，MIMU)，采样频率为200 Hz。 其陀螺仪和加速度计性能参数见表3 所示。 GPS 的采样频率为1 Hz，光纤惯导系统的采样频率为200 Hz。 采用光纤惯导与GPS 组合导航系统传递对准的结果作为参考基准。

图10 车载实验平台

表3 自制的MIMU 传感器特性

图11～图14 分别为载体的运动轨迹，参考的姿态角以及GPS 的速度输出。 图15 为改进前后的观测矢量，由图可得RUSQUE 法滤除了观测矢量中的野值。 图16 为RUSQUE 算法与传递对准估计的陀螺零偏对比曲线。

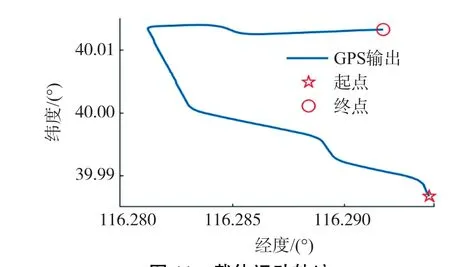
图11 载体运动轨迹

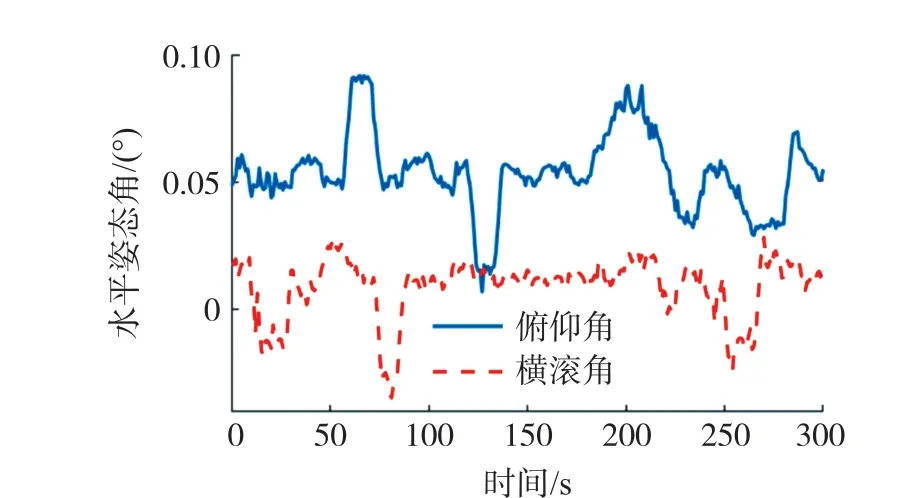
图12 参考水平姿态角

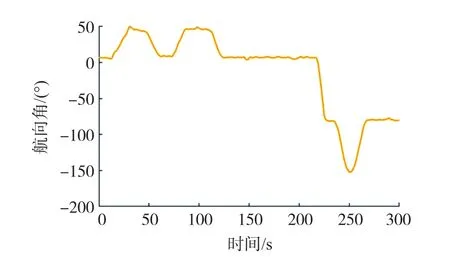
图13 参考航向角

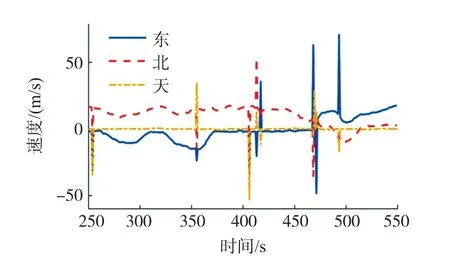
图14 GPS 速度输出

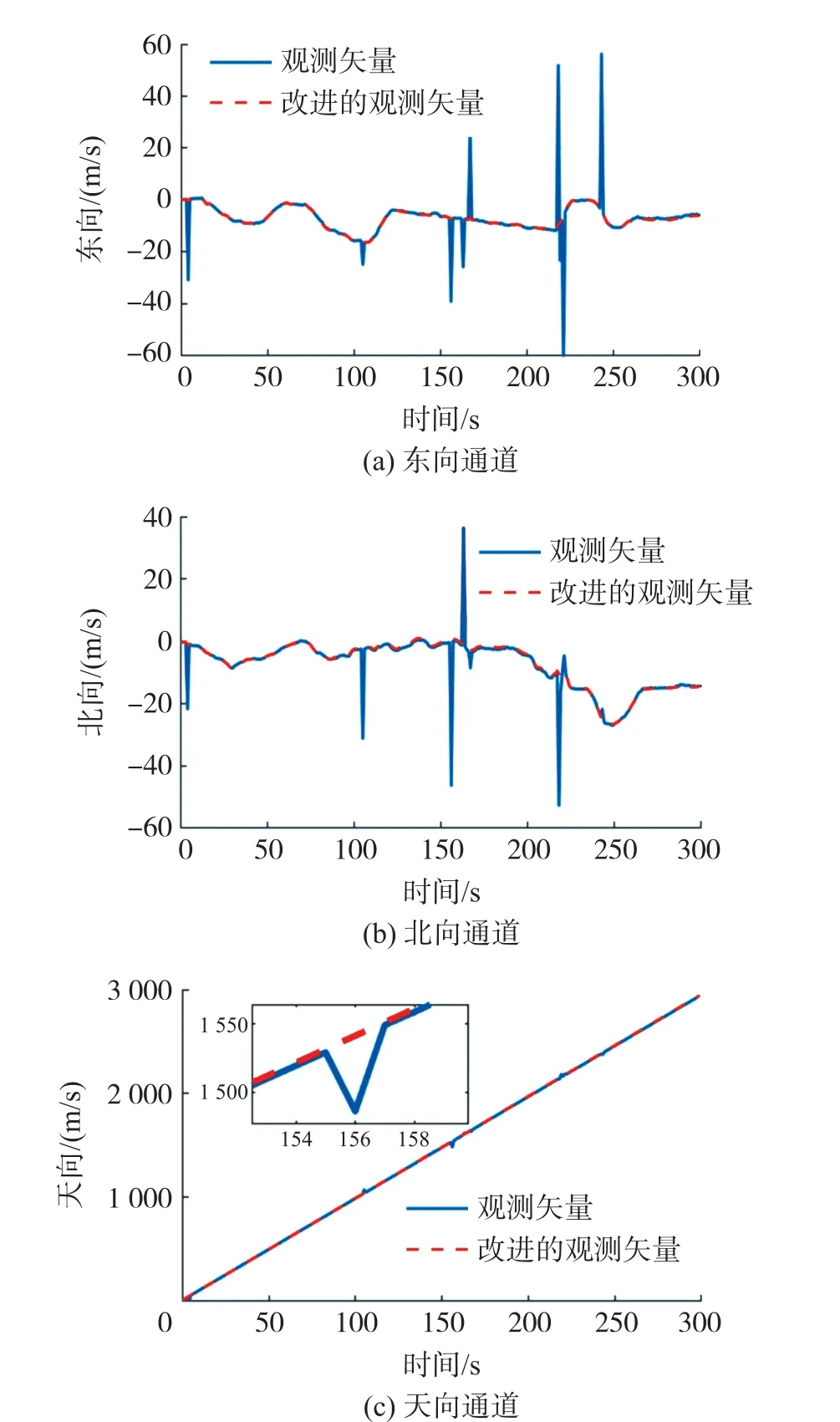
图15 改进前后的参考矢量

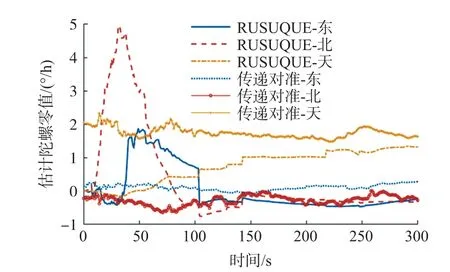
图16 陀螺零偏估计

图17～图19 为五种方案的对准结果图。 在野值的影响下，OBA 法与USQUE 法的对准曲线图都出现了锯齿状的波动，在航向误差图中尤为明显，使得两种算法的对准结果不理想。 但是RUSQUE 算法去除了观测矢量中的野值，所以对准误差曲线呈现了平稳的特性。 当没有野值时，OBA 法的航向角误差曲线由于陀螺零偏累积误差呈波动特性，USQUE 法因在状态方程中去除了陀螺零偏使得航向角误差曲线趋于平稳。 当对准过程经过15s 后，方案2，4 和5 的俯仰角小于0.1°，横滚角误差小于0.13°。 航向角方面，200 s～300 s 之间三种方案的误差均值分别为－0.371 8°，0.241 4°和－0.351 5°，标准差分别为0.046 5°，0.118 4°和0.049 6°。 虽然方案4 的均值优于方案2 与5，但是陀螺零偏的影响导致其误差标准差将近于另两者的3 倍，因此跑车实验也验证了本文提出的算法的鲁棒性以及对于陀螺零偏累积误差的抑制效果。

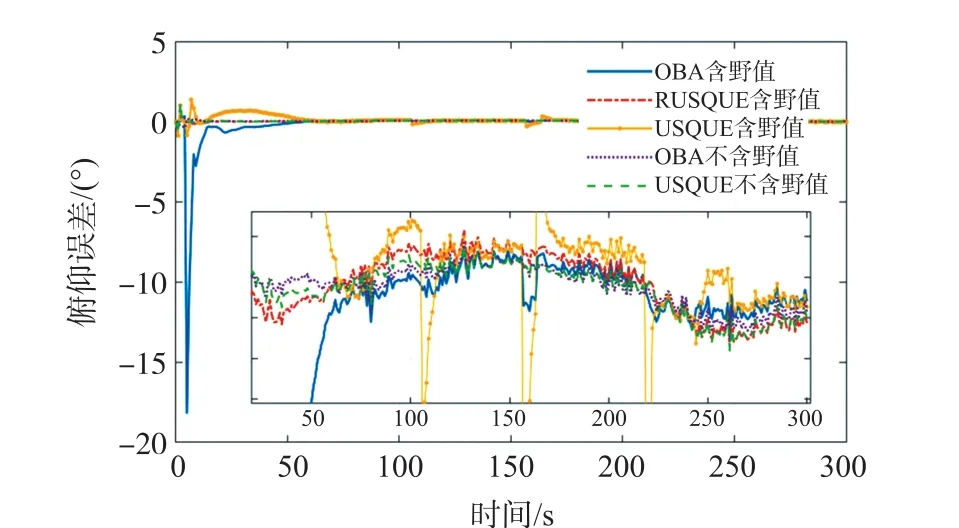
图17 俯仰角误差

图18 横滚角误差

图19 航向角误差

6 结论

针对传统算法在GPS 辅助的低精度惯性导航系统动基座初始对准中易受到陀螺零偏和GPS 野值的影响，本文提出了鲁棒无迹四元数姿态估计算法。 仿真和跑车实验表明，当GPS 中含有野值时，该算法能滤除观测矢量中的野值，同时陀螺零偏导致航向角误差曲线呈波动特性的问题也能得到改善，验证了本文设计的算法相较于传统的算法更有优势。