基于模糊PID的液压伺服比例控制系统设计

2021-03-13阚玉锦李思遥丁响林

兰州工业学院学报 2021年1期

阚玉锦，李思遥，丁响林

(安徽机电职业技术学院机械工程学院，安徽芜湖 241002)

20世纪80年代后期，比例控制系统结构设计得到进一步完善，进入了一个快速发展阶段[1-2].国内对于伺服比例控制系统的研究多集中在各大高校，有学者在系统中采用机械转换器提高系统的响应时间，还有学者研究异型永久磁铁，以期提高系统的驱动力.除此之外，还有学者研究数字控制以提高系统的控制性能[3-4].

本文设计的液压伺服比例控制系统硬件，在前人设计的硬件基础上，考虑系统操作的简便性，使液压伺服比例控制系统具有单位功率质量小、散热速度快、响应速度快、比例控制精度高、负载刚度大等特点.

1 硬件设计

1.1 系统框架设计

在液压伺服比例控制系统中，引入电气、电子技术.在比例控制系统硬件中，增加指令、检测反馈、控制等元件.系统可以实现液压伺服比例控制，检测结果偏差校正，并放大液压伺服比例的初始比例值.此次设计的液压伺服比例控制系统框架如图1所示.

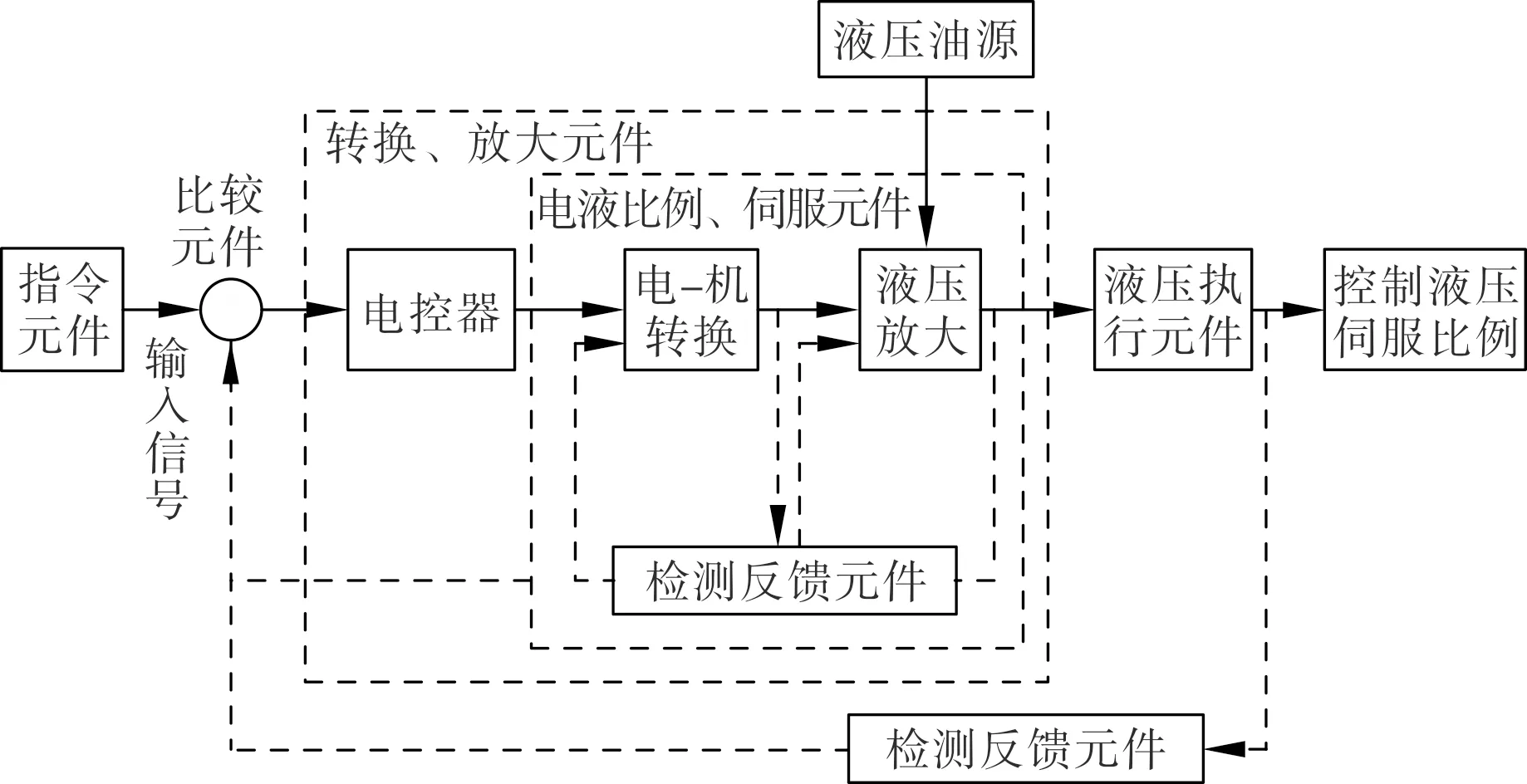
图1 液压伺服比例控制系统框架

图1中共装备了指令元件、比较元件、检测反馈元件、液压执行元件、放大转换控制元件、电液比例伺服元件等6个元件.其中：指令元件用于输入控制信号，即液压伺服比例的录入、各种电气电子硬件运行指令的输入；比较元件主要用于闭环控制，辅助系统调整信号[5]；检测反馈元件主要是各类传感器，用于检测系统的输出变量、中间变量，并反馈检测结果[6]；液压执行元件主要包括液压缸和液压马达等硬件，根据控制指令对液压伺服比例进行控制；放大转换控制元件的主要作用是将输入信号、偏差信号进行放大处理，并将其转换成对应的液压信号[7].

1.2 主要元件硬件参数

对于图1中液压伺服比例数据的采集，将采用数据采集卡采集液压伺服比例数据.

对于电液比例伺服阀，选取4EWRE6E16型号，增加比例控制系统的响应频率，降低反向误差；对于比例放大器，选择VT-VRPA-2型号，可以与比例伺服阀配套使用.

此次设计系统选择的检测反馈元件为位移传感器，反馈液压伺服比例传输的位移信号.所以，位移传感器需要具有测量精度高、反应速度快、感应范围大等特点[8].因此选取LS1679型号的光栅尺位移传感器，作为此次比例控制系统的检测反馈元件.系统硬件选取的主要元件参数如表1～3所示.

表1 数据采集卡元件参数

表2 电液比例伺服阀元件参数

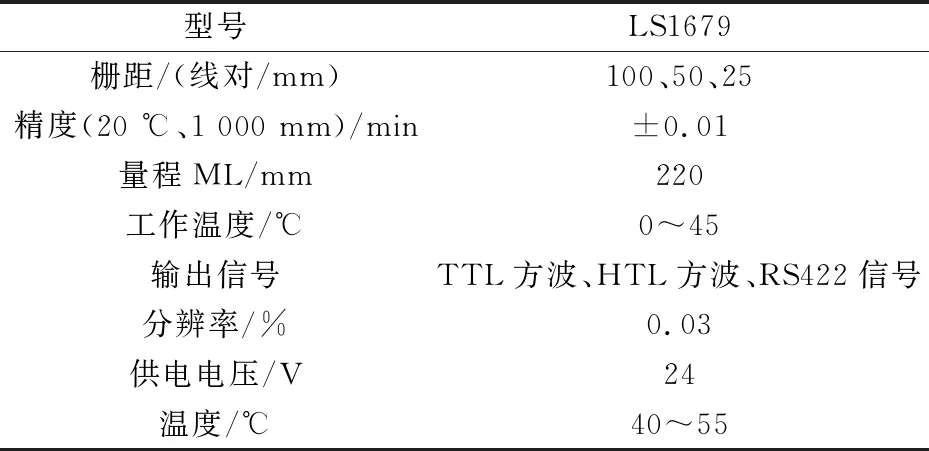
表3 位移传感器元件参数

2 软件设计

在此次设计的液压伺服比例控制系统硬件基础上，利用模糊PID所具有的良好鲁棒性和软件计算控制特点，完成液压伺服比例控制系统软件设计，从而促使系统可以自主控制液压伺服比例.

2.1 确定系统比例控制最优参数

当前液压伺服比例控制中，存在控制传递函数的3个参数，即比例放大r系数Kr、积分i的时间常数Ti和微分d的时间常数Td[9].因此此次设计选取最优的Kr、Ti、Td这3个参数，增加系统控制的精准度.

确定Kr需要先确定比例p系数Kp，因此设积分系数为Ki，微分系数为Kd.让Ki=Kd=0，将Kr逐渐从1增加到50，此时可以通过仿真确定最优Kp范围.在这个过程中，需要从小到大不断改变Kr，此时系统会处于等幅振荡的临界稳定状态，产生临界增益和震荡周期2个数值.当系统处于响应快、超调较小、稳态误差在要求范围内时，加入Ti和Td增加系统产生的积分效应，减小系统稳态误差，并不断试调Kr、Ti和Td，至获得满意的控制效果为止，此时得到的这3个参数即为系统比例控制最优参数.

2.2 制定模糊PID控制规则

(1)

式中：i表示模糊蕴含关系条数；Ei、Ci、ΔUi、Ui均表示模糊集[10].

此时，在如(1)式所示的控制规则下，输出隶属函数模糊蕴含关系，则第i条模糊蕴含关系Ri的表达式为

Ri=Ei×Ci×Ui，

(2)

式中：×表示输出规则运算的算子[11].

而系统中控制规则的制定，是由输入与复合推理规则推出的，则有

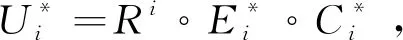
(3)

此时，即可根据上述内容制定系统液压伺服比例控制判决规则，则有

(4)

式中：xi表示液压伺服比例控制系统在运行时的值；Ki的取值为2.1节确定的参数值.

上述即为液压伺服比例控制规则，根据这个规则，即可控制液压伺服比例.

2.3 控制液压伺服比例

基于此次系统设计制定的模糊PID控制规则，其液压伺服比例控制过程如图2所示.

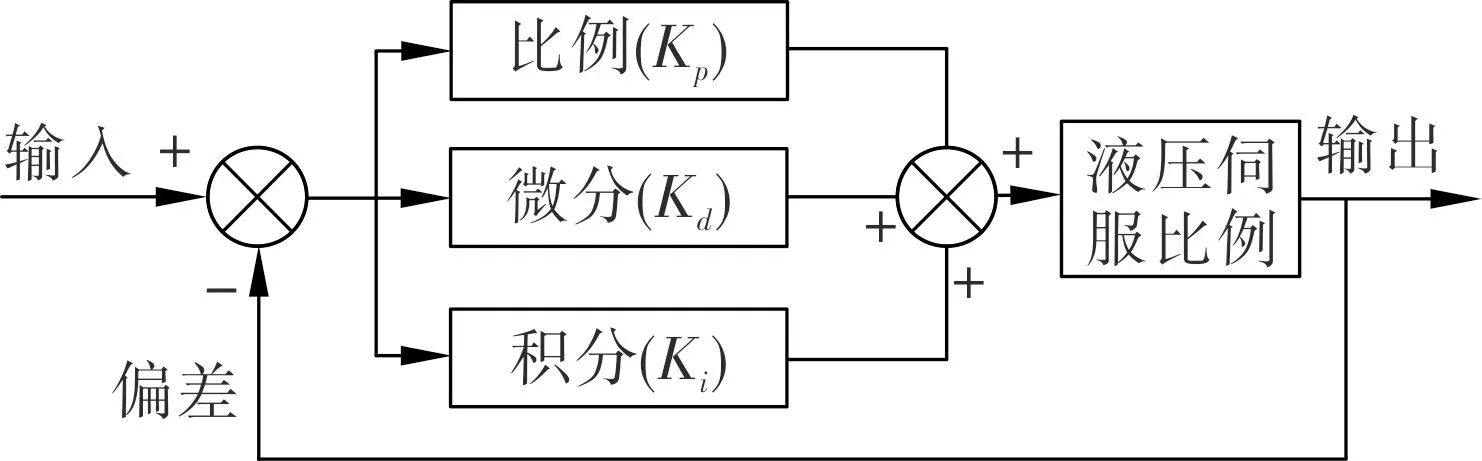
图2 液压伺服比例控制过程

由图2可以看出，基于模糊PID控制规则控制液压伺服比例，是从给定信号r和实际输出信号y之间构成的偏差值e，则有

e=r-y.

(5)

此时，将2.1节计算的最优参数进行叠加，构成新的控制量来控制液压伺服比例，则其控制方程为

(6)

式中：t表示液压伺服比例变量值.

此时，(6)式即为液压伺服比例最终控制结果.综上所述，完成了液压伺服比例控制系统软件部分的设计.此次设计的液压伺服比例控制系统，通过确定最优控制参数和所制定的模糊PID控制规则，可以准确控制液压伺服比例.

3 系统仿真测试

3.1 试验设计

选择市场上通用的液压伺服系统作为此次液压伺服比例控制系统的控制对象.对于系统仿真平台，选择具有基本液压元件库和电信号源库的AMESim软件，作为此次系统测试的仿真平台.其仿真步骤如下：

1) 根据此次设计的液压伺服比例控制系统，在AMESim仿真平台上，寻找到相应的物理模型，建立AMESim仿真系统模型；

2) 给建立系统模型时选择的系统元件确定正确的数学模型；

3) 为确定的数学模型中的元件设置具体的数学参数，校准元件性能；

4) 启动AMESim仿真平台，进行系统仿真测试，并绘制出仿真结果曲线.

此时，改变电磁换向阀的固有频率，对比系统的进出口流速变化，并将此次设计的液压伺服比例控制系统作为A系统，将文献[1]中设计的基于双层模糊控制方法的非线性电液伺服系统与文献[2]中的基于大脑情感学习模型的参考自适应液压伺服控制系统分别作为B系统和C系统.

3.2 系统运行时进口流速对比试验

在此次试验设计确定的系统仿真测试流程基础上，对系统的电磁换向阀固有频率进行测试.在系统其他功能正常的环境下，将电磁换向阀固有频率设置为80 Hz和200 Hz 2个档次，对比3组系统在控制液压伺服比例时，系统进口产生的流速变化.其流速变化对比曲线如图3所示.

由图3(a)可以看出：当电磁换向阀固有频率为80 Hz时，3组系统的进口流速都在可控范围内；C系统的进口流速波动最为剧烈，起伏点多达6处；B系统的进口流速虽然优于C系统，但是流速波动还是具有比较大的跳动性，其起伏点也达到了3处；A系统的进口流速已经没有明显的起伏，基本处于平缓状态.由此可见，此次设计的比例控制系统在电磁换向阀固有频率处于80 Hz的运行状态时，进口流速运行稳定，还可以继续增大电磁换向阀固有频率.

由图3(b)可以看出：当电磁换向阀固有频率为200 Hz时，B系统进口流速变化已经非常剧烈，比例控制系统已经无法正常工作，已经不能控制液压伺服比例；C系统进口流速变化虽然强于B系统，但相对80 Hz的电磁换向阀固有频率，此时C系统的进口流速已经急剧增加，虽然还可以勉强控制液压伺服比例，但依然难以达到精准；而A系统进口流速变化虽较电磁换向阀固有频率80 Hz时有所增加，但是依然在可控制的范围内.由此可见，此次设计的比例控制系统在电磁换向阀固有频率处于200 Hz的运行状态时，依然可以稳定运行.

(a) 80 Hz

综合上述试验发现，电磁换向阀固有频率越低，系统进口流速运行越稳定，但是也会降低系统运行的工作效率；而此次设计的液压伺服比例控制系统，具有较高的工作频率.

3.3 系统运行时出口流速对比试验

将电磁换向阀固有频率设置为80 Hz和200 Hz 2个档次，对比3组系统在控制液压伺服比例时，系统出口产生的流速变化，并与上组试验中进口流速的差值进行比较.其流速变化对比曲线如图4所示.

由图4(a)可以看出：当电磁换向阀固有频率为80 Hz时，3组系统出口流速都在可控范围内；但是B系统的出口流速波动最为剧烈，时间处于10～14 s之间时，出口流速在-1.7～0.4 m/s之间跳动性较大；C系统的出口流速波动虽低于B系统，但依然处于不稳定状态，且与进口流速之间的差值明显大于B系统；而A系统出口流速的波动最为平稳，且与进口流速之间的差值是3组系统中最小的.由此可见，此次设计的比例控制系统在电磁换向阀固有频率处于80 Hz的运行状态时，出口流速运行稳定，还可以继续增大电磁换向阀固有频率.

(a) 80 Hz

由图4(b)可以看出：当电磁换向阀固有频率为200 Hz时，B、C系统的出口流速已经无法精确控制，且进出口流速之间的差值较80 Hz时有所增加，但是B系统的出口流速与进口流速之间的差值明显小于C系统；而A系统在电磁换向阀固有频率为200 Hz时，出口流速虽然具有较大的跳动性，但是在可控范围内，进出口之间的流速虽然比80 Hz时有所增加，但是增加较少，且明显低于B系统和C系统.由此可见，此次设计的比例控制系统在电磁换向阀固有频率200 Hz的运行状态时，进出口间流速差值未出现明显增加现象，对于系统出口流速处于可控范围内，可以承受更高的工作效率.

由上述2组试验可知，基于模糊PID的比例控制系统可以承受200 Hz的电磁换向阀固有频率，且进出口之间的流速也都处于可控范围内，且流速变化相对稳定.产生这一结果的原因在于，该系统通过确定最优控制参数设计了相应的模糊PID控制规则，从而能够准确控制液压伺服比例.