对称型双塔连体高层结构抗震性能分析

谭丽君，雷庆关

(安徽建筑大学 土木工程学院，安徽 合肥 230601)

由于建筑效果或者功能的需求，目前国内高层连体建筑的应用较为普遍.连体建筑的抗震性能往往与单体建筑有显著不同，需要开展专门的研究.随着结构复杂程度的日益增加，大量复杂连体结构频繁出现，从而产生显著的扭转效应.尤其当2个单体结构主要振型平动与转动方向不一致时，连体结构在低阶模态就会表现为整体扭转，并包含各自独立的局部振动[1].目前，对于双塔连体结构的研究也越来越多，其中包括自振特性、计算模型、结构抗震试验、动力响应等.国内外针对连体双塔结构的研究很广泛，然而设计人员对于连体高层建筑的设计还缺乏有效的手段和成熟的认识，通常仅仅依靠一般的软件和现有的工程经验，无法充分掌握结构的抗震性能[2].因此，研究双塔连体结构的抗震性能具有重要意义.本文以对称双塔连体结构为研究对象，分析连体结构对对称型双塔高层结构抗震性能的影响.

1 模型建立

本文模型模拟的实际结构为混凝土框架结构的商业办公楼.模型一为双轴对称双塔结构，共19层，第1～4层为结构的底盘，层高为3.8 m，作为商用部分，第5～19层为办公区，层高为3.3 m.结构横向8跨，左右塔楼的柱距为6 m，两塔楼之间柱距为5 m；纵向4跨，柱距为6 m.主要构件截面尺寸：梁截面尺寸600 mm×1 000 mm,混凝土采用C40；第1～4层柱截面尺寸为1 000 mm×1 000 mm混凝土采用C40，楼板厚度150 mm，混凝土采用C30；第5～19层柱截面尺寸为800 mm×800 mm，混凝土采用C40，楼板厚度120 mm，混凝土采用C30.模型二为双轴对称双塔连体结构，与模型一的不同之处为在第15层位置处设置连体结构，连体结构主要构件尺寸与模型一第5～19层结构一致，两模型其余基本参数一致.模型三为单轴对称双塔连体结构，与模型二不同的是左右塔楼不等高，右塔楼层高15层，其余基本参数与模型二一致.建筑设计抗震设防烈度为7度，基本地震加速度为0.15g，场地类别为Ⅱ类，设计地震分组为第二组，特征周期为0.35 s，阻尼比为0.05，水平地震最大影响系数为0.12，周期折减系数为0.85，梁上均布荷载为8 kN/m2，楼面恒荷载为4.5 kN/m2，楼面活荷载为2 kN/m2. 3种模型结构如图1～3所示.

图1 双轴对称双塔结构 图2 双轴对称双塔连体结构 图3 单轴对称双塔连体结构

2 地震反应分析

2.1 模态分析

模态分析方法包含特征向量法和Ritz向量法.本文模型采用Ritz向量法，可以大大减少用于数值分析求解的时间.模态分析是反应谱分析和时程分析的基础，通过模态分析可以得到结构的自振周期、质量参与系数等基本性能参数，对基本参数的分析可以定性判断结构的响应[2-3].本文通过SAP2000对3种模型进行模态分析，得出模型前20阶的自振周期、质量参与系数并进行对比，见表1～3.通过分析表1～3可得：

1) 模型一前20阶振型的质量参与系数百分比之和为99.6%、99.5%；模型二前20阶振型的质量参与系数百分比之和为99.6%、99.3%；模型三前20阶振型的质量参与系数百分比之和为99.9%、99.4%.均满足《建筑抗震设计规范GB50011—2010》[4]计算的振型数应为各振型的参与系数之和不小于总质量的90%.

2) 关于模型前20阶的自振周期，模型一最大，模型二略小于模型一，模型三略小于模型二；关于模型前20阶的质量参与系数，模型一最小，模型二略大于模型一，模型三略大于模型二.说明3个模型结构整体刚度逐渐增大，连体结构可以使结构更安全.

3) 表1中，模型一的前3阶振型分别为沿x向平动(Ux=0.727),沿y向平动(Uy=0.751),扭转(Rz=0.726)；表2中，模型二的前3阶振型分别为沿y向平动(Uy=0.736),沿x向平动(Ux=0.711),扭转(Rz=0.637)；表3中，模型三的前3阶振型为沿y向平动(Uy=0.534)，沿x向平动(Ux=0.693)，扭转(Rz=0.549).3种模型都是在第3阶振型中出现扭转，符合规范要求.

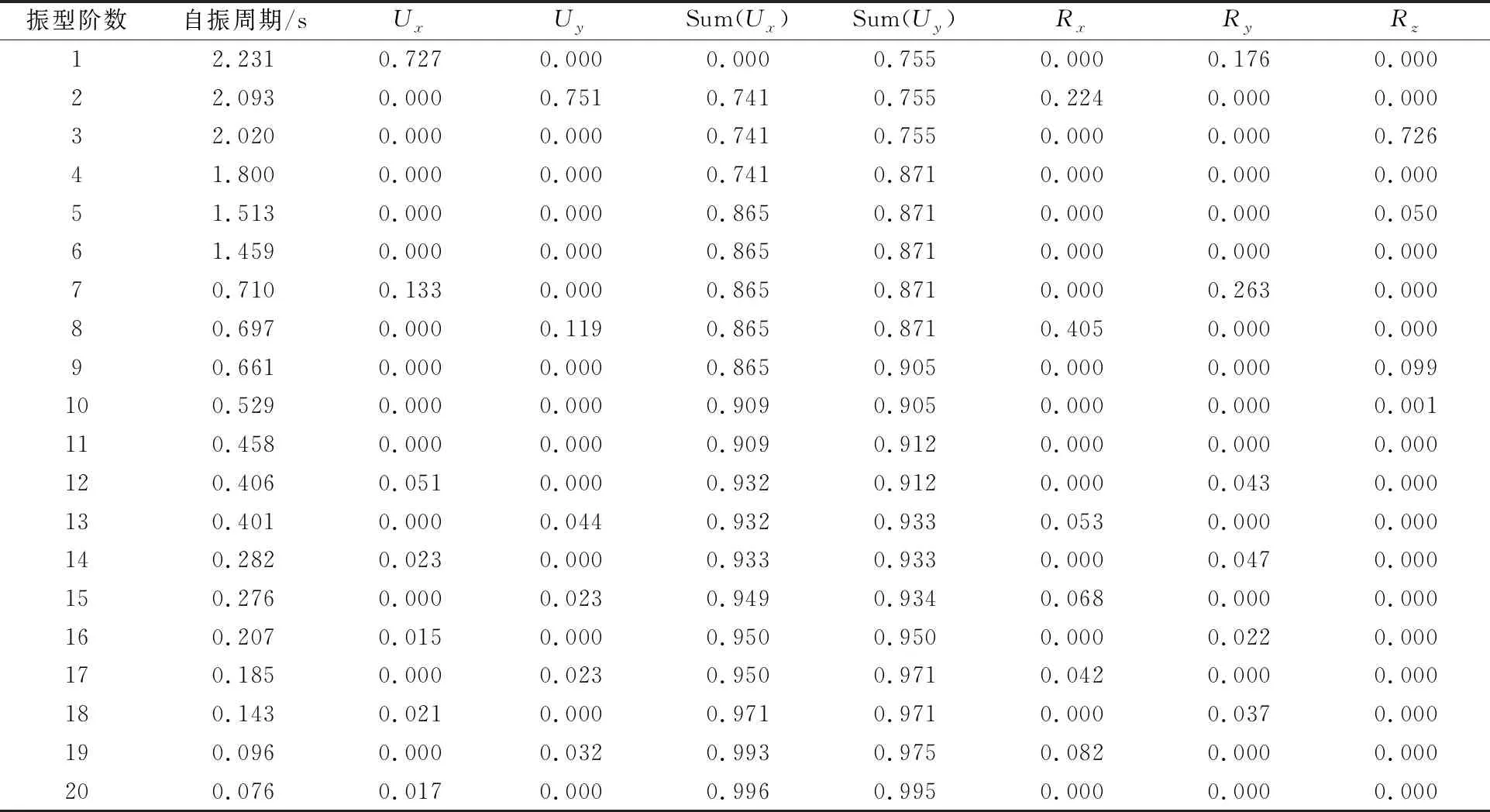
表1 模型一自振周期及质量参与系数

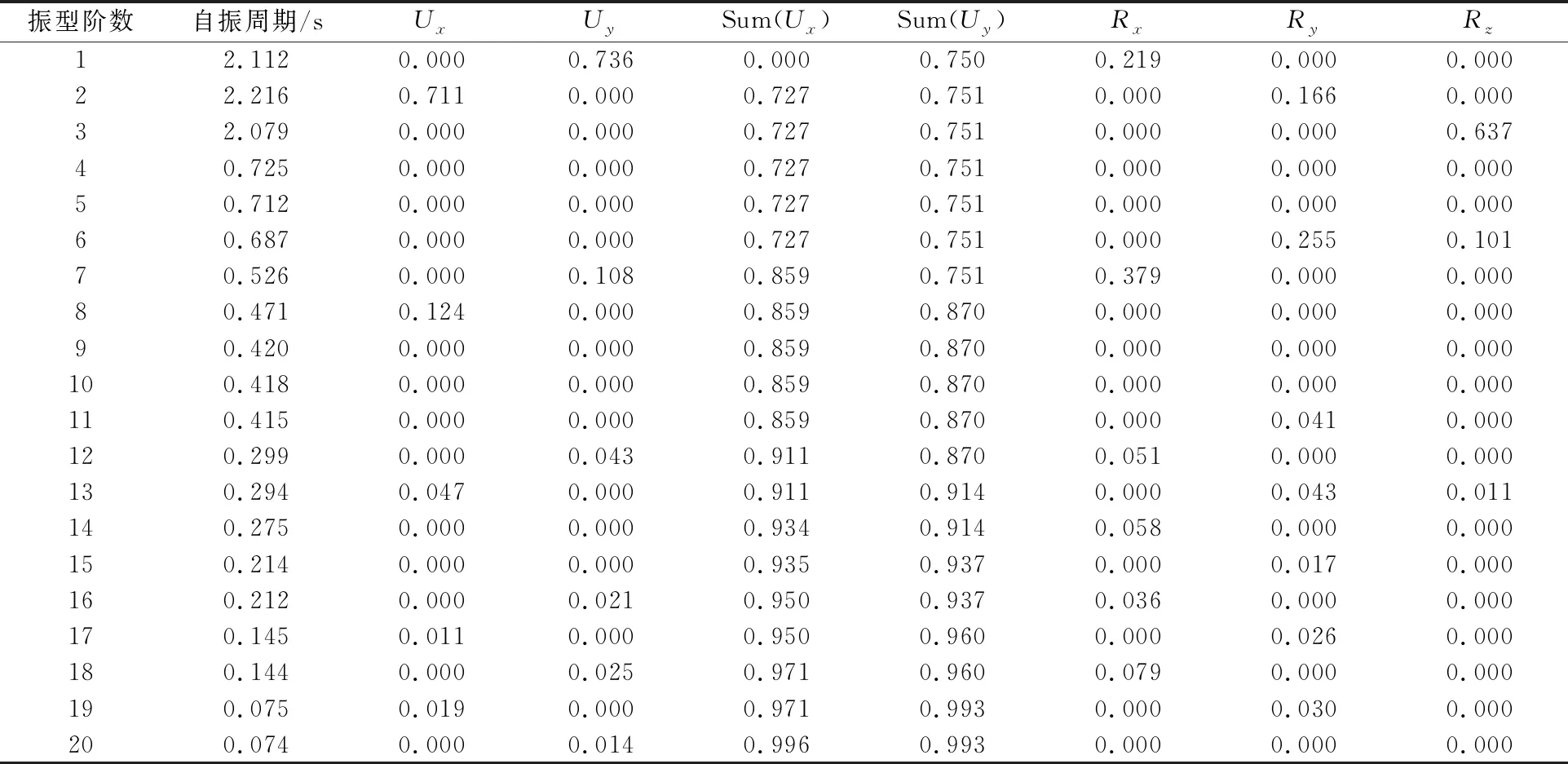
表2 模型二自振周期及质量参与系数

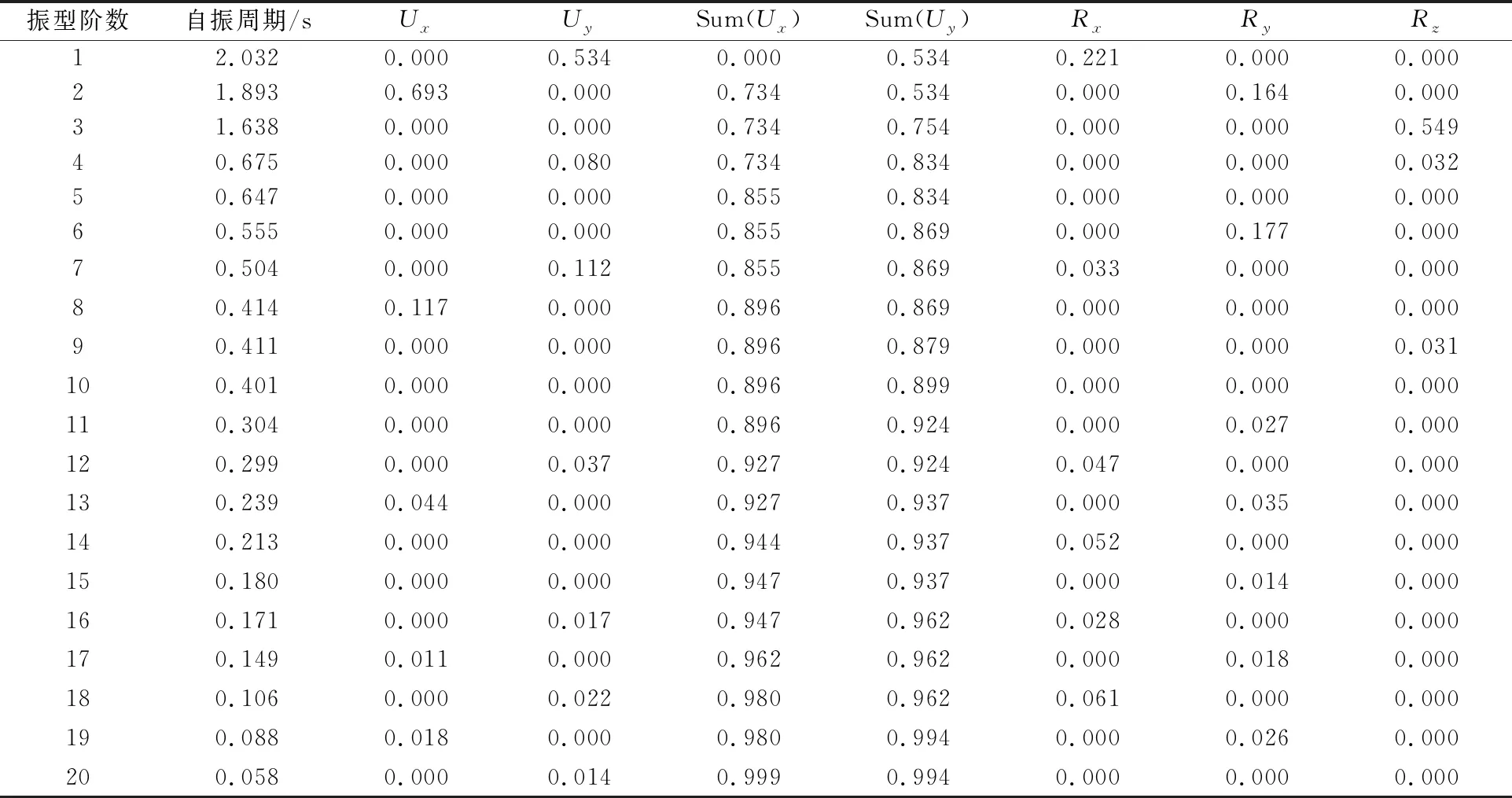
表3 模型三自振周期及质量参与系数

2.2 反应谱分析

反应谱分析方法本质上还是一种静力分析方法，采用该方法将结构的动力特性(结构的自振周期、振型和阻尼)转化为静力分析.反应谱分析理论方法中最为广泛应用的动力计算方法是振型分解反应谱法，是计算多自由度结构体系地震相应的方法之一，其主要原理是振型分解理论和反应谱理论[5].通过求解各阶振型的地震作用，然后进行组合则可求得其地震作用.本文利用反应谱分析法进行分析，可得出3种模型的楼层位移和层间位移角(见表4)，对此曲线如图4～5所示.

由表4和图4～5分析数据可得：模型一、模型二、模型三的最大位移分别为46.63、42.33、41.05 mm，最大位移逐渐减小，说明连体的加入可以减小结构位移，增大结构的侧向刚度，对结构有利[5].模型一的最大层间位移角为1/991，发生在结构第6层；模型二的最大层间位移角为1/1 119，发生在结构第6层；模型三的最大层间位移角为1/1 082，发生在结构第6层.3个模型的层间位移角都满足《建筑抗震设计规范GB50011—2010》[4]要求，结构层间位移角小于1/550.

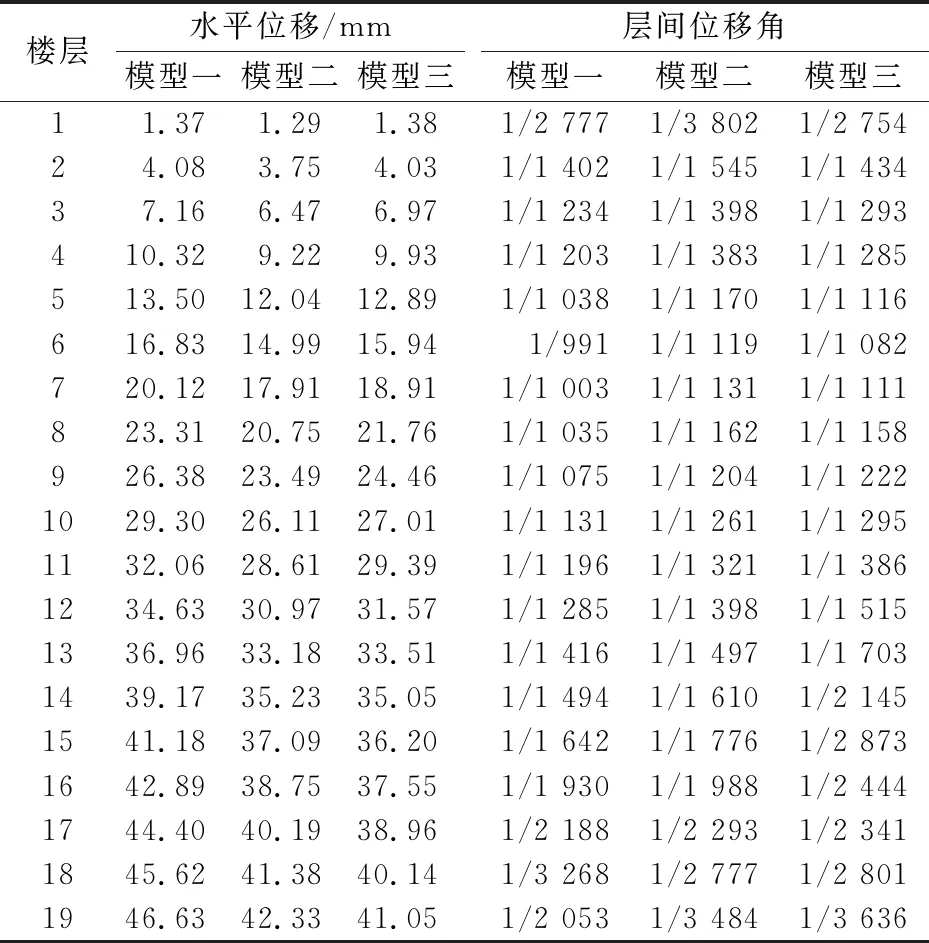
表4 反应谱分析模型楼层位移及层间位移角

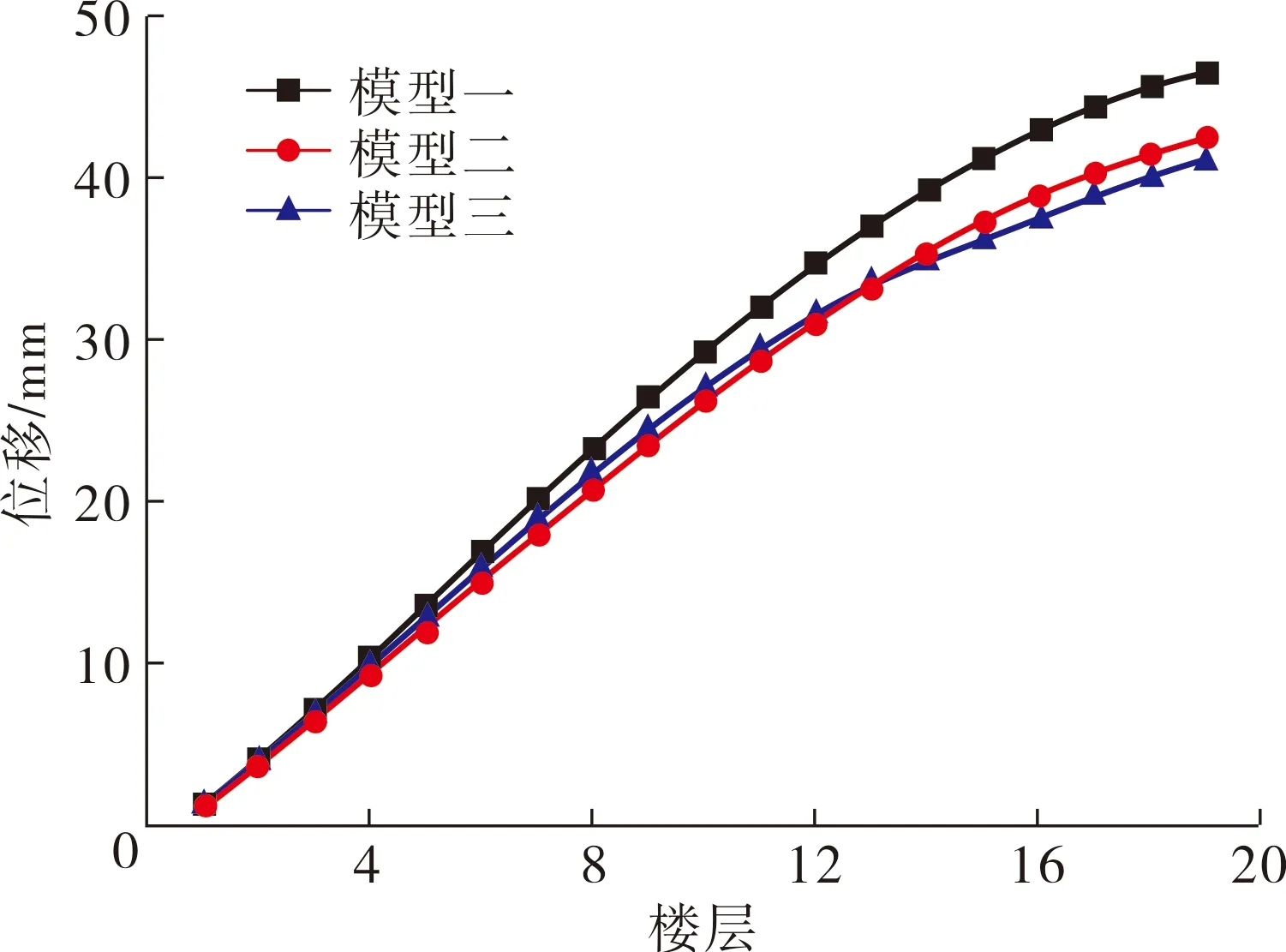
图4 反应谱下楼层最大位移曲线对比

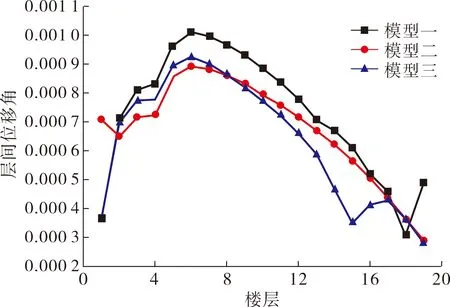
图5 反应谱下楼层最大层间位移角曲线对比

2.3 时程分析

从理论的角度看，时程分析法相对于振型分解反应谱法更为精确和适用，振型分解反应谱法的优点是计算简便，但是不能反映结构在地震作用下非线性的反应过程，因此时程分析方法一般作为高层建筑设计的一种补充分析方法，主要补充反应谱方法在塑性状态下的不足[6].

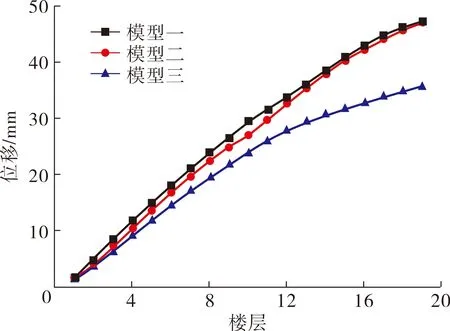
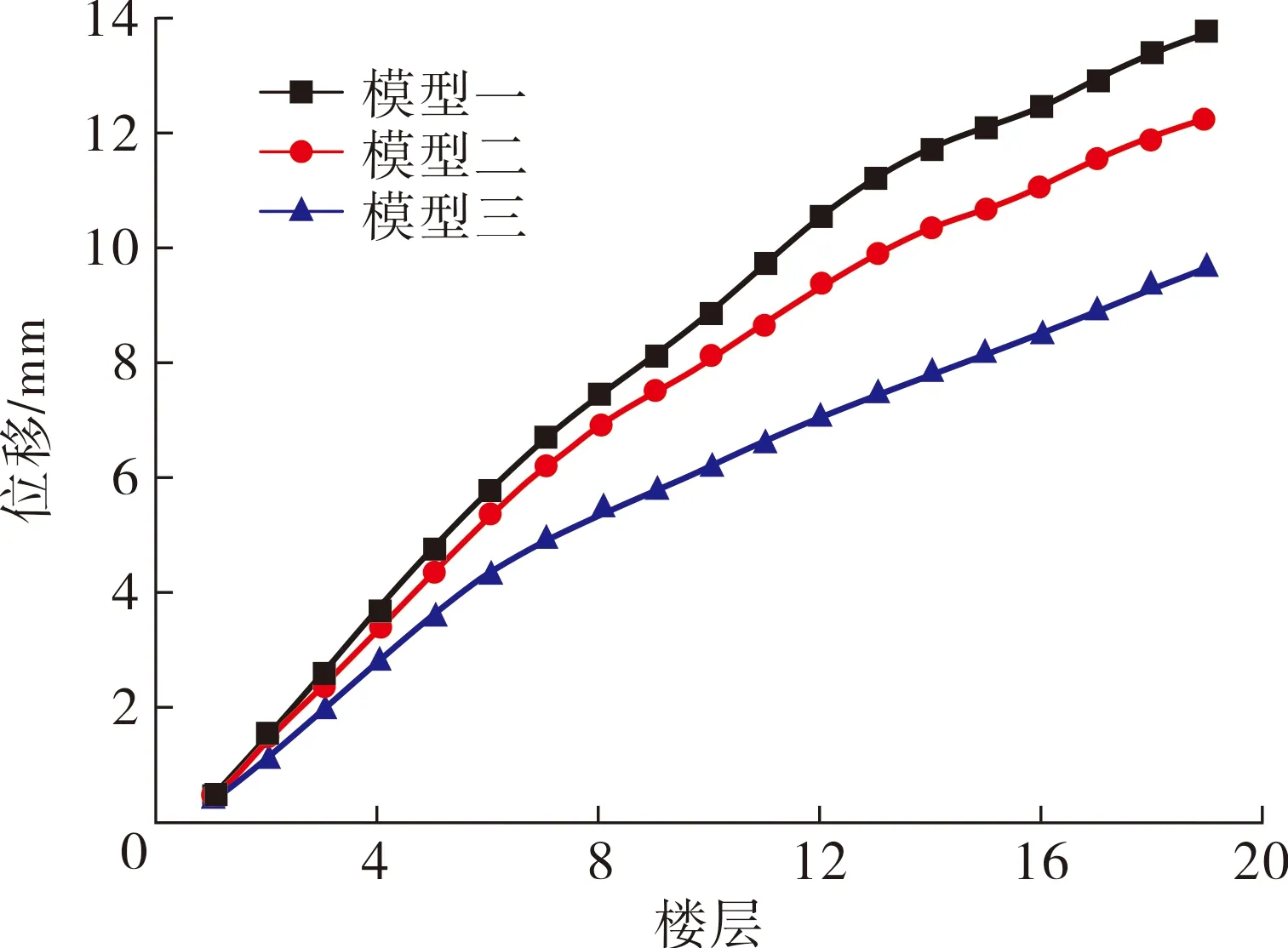
本文选取了2条适合所选场地的地震波，分别是Taft地震波和Lanzhou3地震波.2种波的主要参数有：Taft地震波记录时间间隔为0.02 s，持续时间为30 s，加速峰值为175.9 cm/s2；Lanzhou3地震波的记录时间间隔为0.02 s，持续时间间隔为20 s，加速峰值为196.2 cm/s2[6-7].对3个模型进行时程分析得到3个模型的楼层位移和层间位移角,如表5～7所示.由表5～7可得3个模型楼层位移和层间位移角,包络图如图6～7所示.

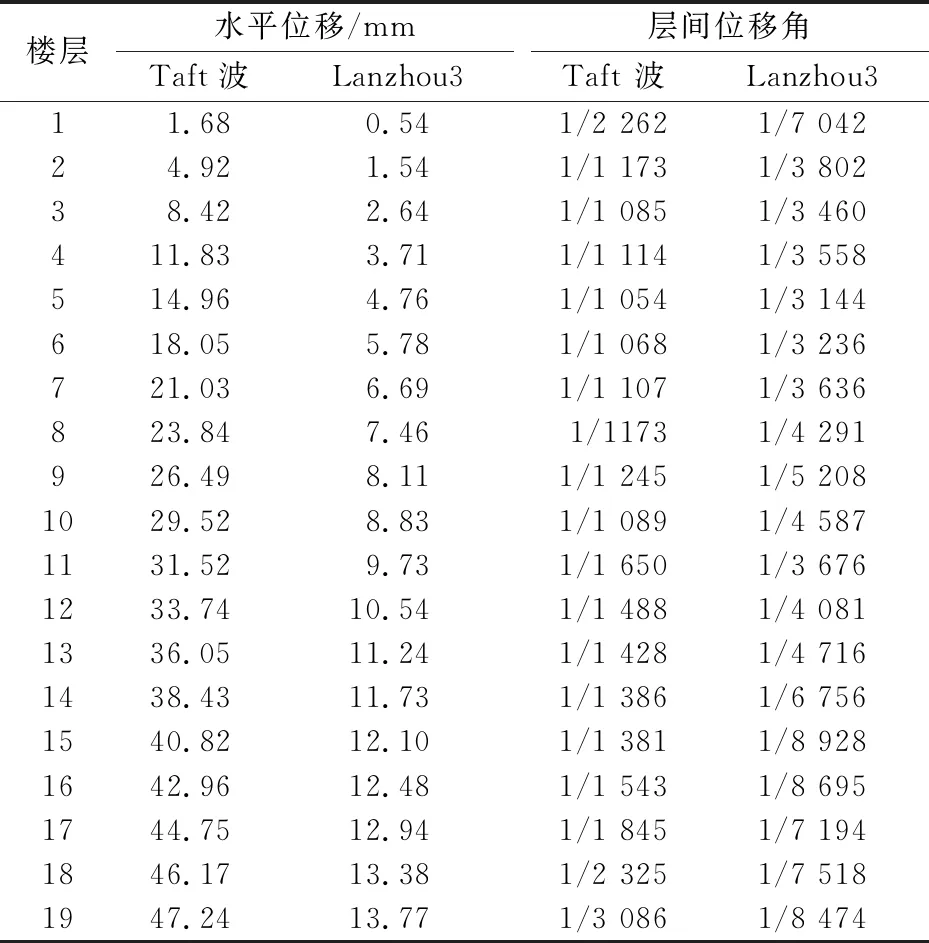
表5 时程分析模型一楼层位移及层间位移角

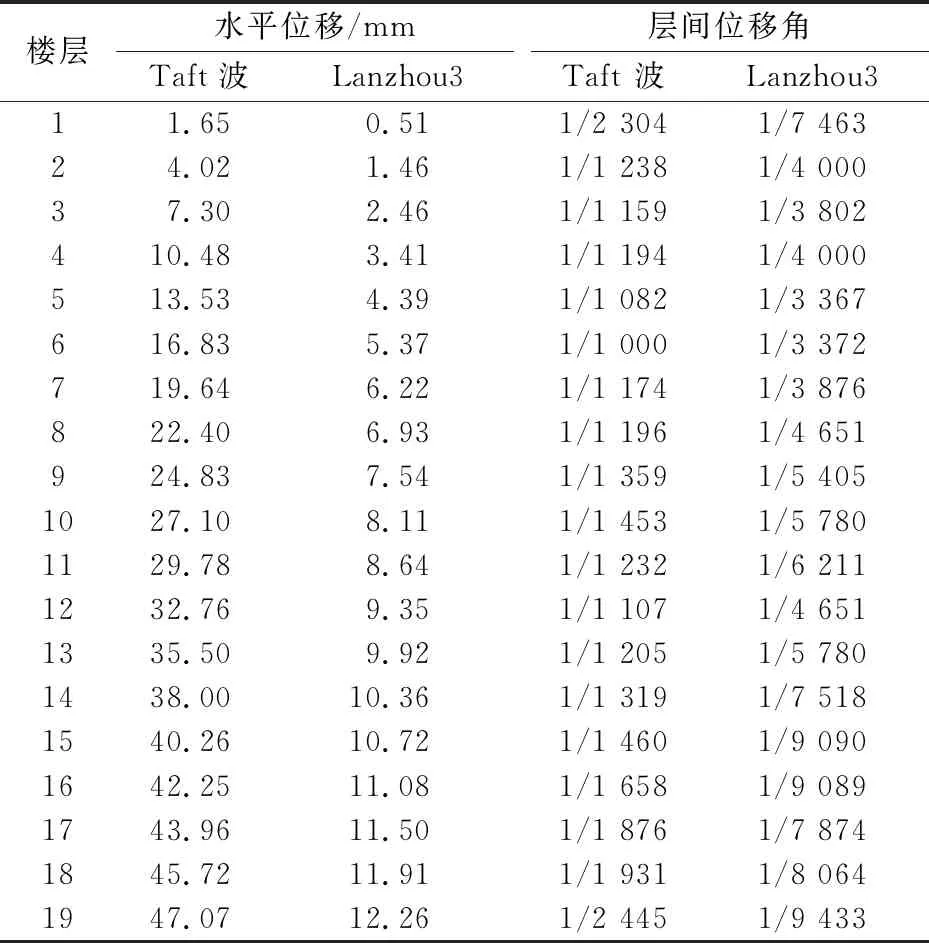
表6 时程分析模型二楼层位移及层间位移角

表7 时程分析模型三楼层位移及层间位移角

(a) 位移

由表5～7和图6～7分析可得：在Taft地震波和Lanzhou3地震波作用下的，模型一最大楼层水平位移分别为47.24、13.77 mm，最大层间位移角分别为1/1 054、1/3 144；模型二最大楼层水平位移分别为47.07、12.26 mm，最大层间位移角分别为1/1 000、1/3 367；模型三最大楼层水平位移分别为35.47mm、9.66 mm，最大层间位移角为1/1 222、1/4 184. 3个模型的层间位移角都满足《建筑抗震设计规范GB50011—2010》[4]要求，结构层间位移角小于1/550.

(a) 位移

3 结论

1) 根据模态分析所得数据，连体结构的加入使得双轴对称双塔结构的自振周期减小，这种现象在单轴对称双塔连体结构上更显著，说明连体结构的加入可以增加结构的抗侧移刚度并对单轴对称双塔连体结构更有效果.根据3个模型的前3阶振型，更说明连体结构可以减少结构的侧移，增加结构的安全[8].

2) 根据反应谱分析所得数据，3种结构模型均在第6层出现最大层间位移角，说明第6层作为塔楼与底盘连接层位置的上一层，是结构的薄弱层，在以后的结构设计和施工中应采取相应措施加强薄弱层的防护.随着连体结构的加入，结构x方向的楼层位移和层间位移角逐渐减小，说明连接体布置使得结构的整体刚度加强，有利于结构抗震[9].

3) 根据时程分析所得数据，对于3种模型进行时程分析得出的顶层位移，Taft地震波比Lanzhou3地震波的都要大，说明同一模型下，不同地震波对结构整体产生的变形是不同的，结构分析时根据实际地震状况来选取地震波.通过3个模型楼层位移和层间位移角包络图可知，在同一种地震波作用下，随着连体结构加入，模型的顶层位移与最大层间位移角均减小，在单轴对称双塔结构中效果更显著[10].因此，对于对称型双塔高层结构，合理地布置连体结构可以提高结构整体的抗震性能，尤其是对于单轴对称双塔结构更应该合理布置连体结构.