足式液压驱动机器人腿机构设计与分析

詹玉新，张玉华，王晓明，周多道

(1.滁州职业技术学院 电气工程学院，安徽 滁州 239000；2.安徽工业大学 机械工程学院，安徽 马鞍山 243002)

近来年，国内外对机器人的各种研究越来越多，由于足式机器人相对于履带式机器人以及轮式机器人在不平整和危险环境中具有较大的机动灵活和优越性，所以在工业、建筑、军事等不同领域的应用越来越广泛[1].由于足式机器人液压驱动具有承载能力大、控制简单、能提供过载保护等优点，对四足液压驱动机器人的研究越来越多[2-5].美国波士顿动力公司研究的“大狗”机器人，在崎岖的道路环境中能够承受复杂154 kg负载的情况下，其运动和速度变换方式多种多样，且在小跑运动过程中平均速度能达到5.6 km/h，跳跃前进过程中其速度可达到11.2 km/h[6].

现有的足式液压驱动机器人主要存在腿机构复杂、运动空间小、驱动力臂变化导致关节驱动力矩不稳定等问题.因此，本文通过仿动物肌肉收缩和松弛原理，设计了一种采用液压驱动、滑轮和绳索牵引传动的机器人单腿机构，该腿机构适用于四足机器人，承载能力大、工作空间大、易于控制[7].

1 腿机构原理分析

根据现有四足机器人和足式液压驱动机器人的整体结构特征分析，本文设计的足式机器人单腿机构关节包括髋关节、膝关节和踝关节，每个关节都有若干个自由度[8].髋关节自由度是由侧摆和俯仰方向自由度组成，其中侧摆方向运动由位于机身的液压缸所控制，膝关节控制前后方向的自由度.踝关节是由足端组成，可沿3个不同方向进行转动.单腿部件由大腿机构、小腿机构和足端组成，足端安装在小腿机构的底部，髋关节和膝关节前后运动均由安装在大腿部件的油缸控制，通过安装在机身的油缸来控制髋关节侧摆运动方向，足端为球形足.综上，本文所设计的单腿机构包括两自由度的髋关节、膝关节以及可沿3个不同方向转动的球形足，其单腿机构如图1所示.

图1中：A为髋关节摆动中心；B为膝关节摆动中心；C为球形足的中心；α为大腿前摆极限角；β为大腿骨向后摆动的极限角；δ为小腿骨相对大腿骨向后摆动的极限角.

1—大腿骨；2—大腿前摆缸；3—大腿前拉索；4—大腿前滑轮；5—小腿前滑轮；6—小腿前拉索；7—小腿前摆缸；8—球形足； 9—小腿骨；10—小腿后杆；11—小腿后拉索；12—小腿后滑轮；13—大腿后滑轮；14—大腿后拉索；15—大腿后摆缸

该腿机构运动原理为：动滑轮沿导向槽移动，将柱塞的推力转变为驱动关节运动的拉力，不仅缩短了柱塞缸的工作行程，使腿机构的结构更加紧凑，而且扩大了关节运动的空间.

当大腿前摆缸伸出时，推动大腿前滑轮移动使大腿前拉索拉紧，从而在拉索力的作用下，驱动大腿骨相对于髋关节向前摆动；同时，大腿后拉索带动大腿后滑轮移动使大腿后摆缸缩回.反之，当大腿后摆缸伸出时，推动大腿后滑轮移动使大腿后拉索拉紧，从而驱动大腿骨绕着髋关节向后摆动；同时，大腿前拉索带动大腿前滑轮移动使大腿前摆缸缩回.

当小腿前摆缸伸出时，推动小腿前滑轮移动使小腿前拉索拉紧，从而驱动小腿骨向前摆动；同时，小腿后拉索带动小腿后滑轮移动使小腿后摆缸缩回.反之，当小腿后摆缸伸出时，推动小腿后滑轮移动使小腿后拉索拉紧，从而驱动小腿骨向后摆动；同时，小腿前拉索带动小腿前滑轮移动，使小腿前摆缸缩回.

2 腿机构运动分析

腿机构运动学分析不仅是腿机构各项研究的基础，也是运动控制、腿机构力学研究以及详细结构设计的一项重要方法.机器人足端工作空间是衡量机器人在运动过程中适应性的一个重要参数，因此应对单腿机构进行正运动学分析，以得出足端点在髋关节坐标系间的位置以及求出足端的速度与加速度，并通过蒙特卡洛法得出足端在摆角范围内的工作区域，验证其满足运动功能要求.

机器人在运动过程中，位于摆动相的各单腿可理解为机械臂，为一串联式开链结构，包括髋关节、膝关节2条腿节.而处于支撑相的腿与机体构成了并联式多闭链自由度结构.所以计算各腿骨上运动关节与足端关系，就要确定出各腿骨之间的相对运动与位置和姿势关系.机器人的各单腿机构可看做是由其各驱动关节及腿杆件串联连接起来的连杆机构，然后在每一个连杆上建立坐标系，并通过相邻两连杆之间的坐标变换来描述单腿机构各部件之间的相对位置和姿态关系.利用“D-H”法则以及相邻两连杆之间的变换矩阵，建立并分析大小腿两自由度位置，如图2所示.

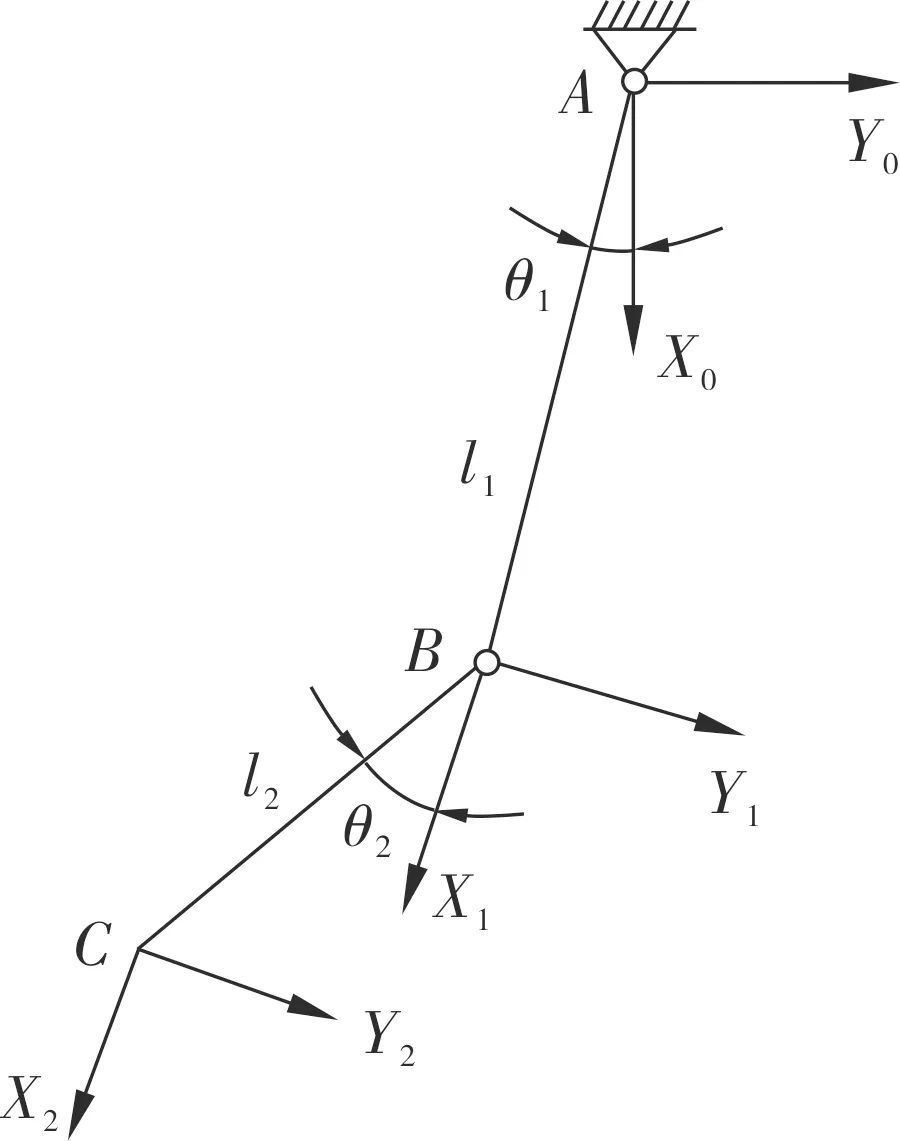
图2 大小腿两自由度位置

由图2可知：X轴方向为重力方向，Y轴方向为机器人前进方向，原点为各关节轴线与相邻关节间公垂线的交点；在髋关节、膝关节和足末端分别建立3个坐标系，其名称分别记为(X0AY0)、(X1BY1)、(X2CY2)，且以(X0AY0)为基坐标系.图2中：θ1和θ2分别表示髋关节和膝关节的摆动角度，即大腿骨相对髋关节摆动的角度和小腿骨相对大腿骨向后摆动的角度；l1和l2分别表示大腿骨和小腿骨的长度.

根据“D-H”法则，可以得出单腿机构的“D-H”参数，如表1所示.

表1 单腿“D-H”参数

用Ai-1,i来表示相邻2个关节之间的坐标齐次变换矩阵，并以各齐次变换矩阵相乘从而可以得出1个总的变换矩阵，最后通过总的坐标变换矩阵就可以求解出各关节摆动角度与足末端的位姿关系.此变换矩阵的通式Ai-1,i为

Rot(Zi-1,θi)·Trans(0,0,di)·Trans(li,0,0)·Rot(xi,αi)=

(1)

通过表1中的数据以及相邻关节齐次坐标变换矩阵，从而求得坐标系{0}与{1}的坐标变换矩阵以及{1}与{2}之间的坐标变换矩阵，即

(2)

(3)

则足端坐标系相对于髋关节坐标系的总变换矩阵T为

T=A0,1A1,2=

(4)

T又称为机器人的位置与姿态矩阵.足端固连坐标系相对于髋关节坐标系的坐标变换矩阵为

(5)

从而可以求出腿部足端点位置坐标为

(6)

式中：Cx、Cy、Cz分别为足末端点在髋关节坐标系处的位置.

在机器人的腿部设计中，假定髋关节距足端中心的高度H不大于800 mm，则大腿和小腿的长度均在[0，800]范围内.在腿的长度比例选取时，一般是通过足端工作空间的面积大小和机器人在一个步行周期中所消耗的能量大小进行综合比较.通过计算得出大腿骨长度l1=410 mm，小腿骨长度l2=340 mm时为大小腿长度的最优设计.此外，已知腿机构的关节变量范围为：髋关节前摆幅角75°，后摆幅角60°；膝关节变量范围为[0，135°].再通过足末端点在髋关节处基坐标系中的位置，根据机器人足端工作空间求解方法——蒙特卡洛法[9]，从而可以得出2自由度腿机构单腿足端在摆角范围内的工作区域，如图3所示.

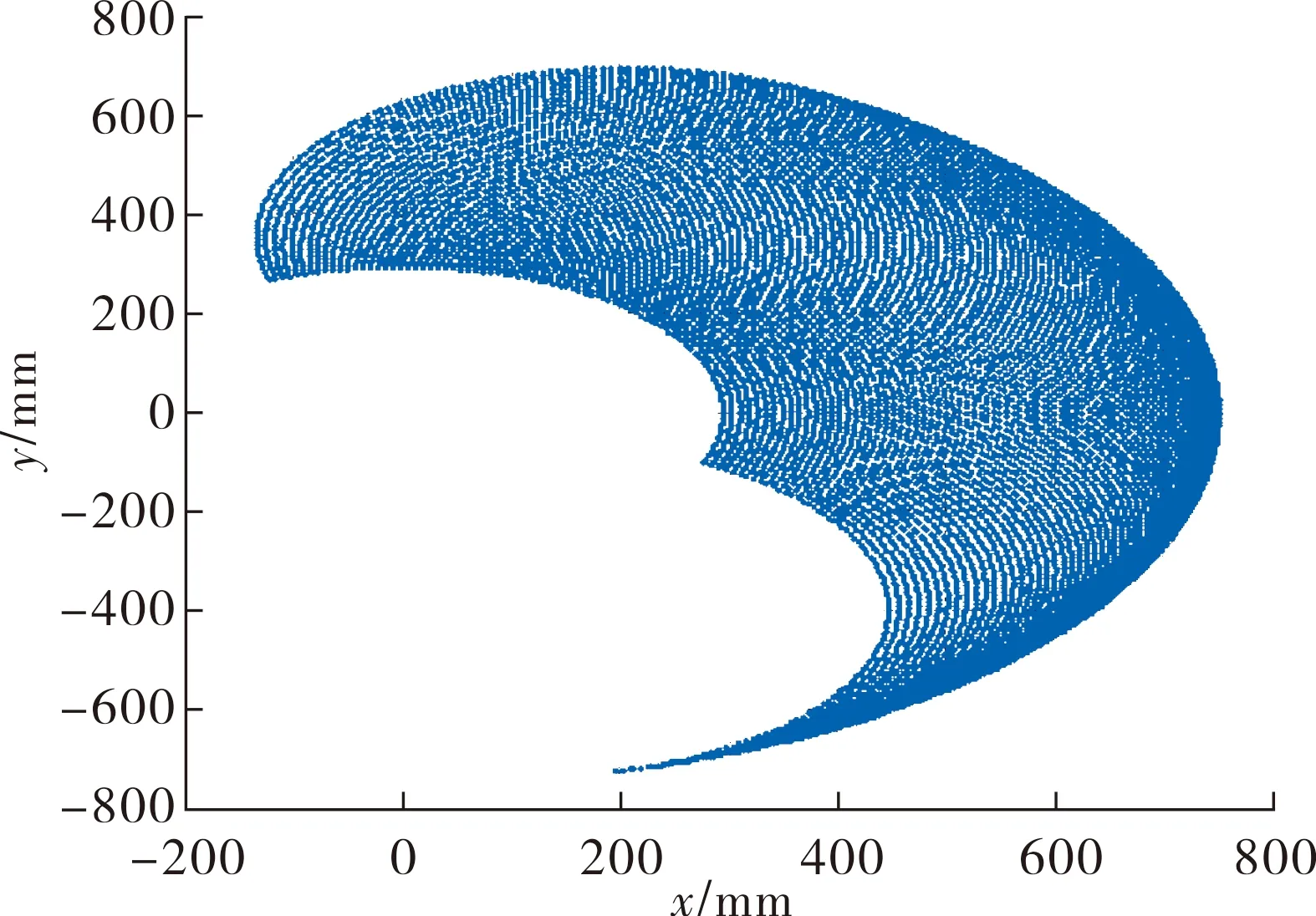
图3 腿机构单腿足端工作区域

图3中：x表示足端到髋关节的垂直距离，y表示足端跨步步长.观察足端在x、y方向上的运动范围，其腿机构末端的足端中心可以到达的位置距离髋关节最大距离为750 mm，腿机构的实际最大跨越步长为724 mm，腿的跨抬高度为556 mm，这个工作空间满足实际要求.

3 仿真分析

根据四足机器人的结构参数要求，通过在三维软件中建立其实体模型，并导入Adams软件，同时依据样机模型及仿真要求，添加相关的约束和接触力，从而很快地建立起四足机器人的虚拟样机模型.通过分析可知，简化后的虚拟样机模型共有8个旋转副，12个固定副，分别为：机体和腿支架之间添加固定副(4个)；腿支架和髋关节轴之间添加固定副(4个)；大腿骨和髋关节轴之间添加转动副(4个)；大腿骨和膝关节轴添加固定副(4个)；小腿骨和膝关节轴之间添加转动副(4个).添加约束后，机体与腿支架和髋关节轴固定在一起，大腿骨绕髋关节轴前后摆动，大腿骨与膝关节轴固连后，小腿骨相对大腿骨前后摆动.添加约束和接触力后的虚拟样机模型见图4.

图4 虚拟样机模型

对于四足机器人而言，其运动步态方式主要包括静态行走步态、单腿跳跃步态和对角小跑步态3种.静态行走步态是指行走过程中，只有3条腿或4条腿支撑于地面，其占空系数大于等于0.75，稳定性最高.单腿跳跃步态是指机器人在行走中始终只有1条腿与地面保持接触，占空系数小于0.5.对角小跑步态是指机器人处于对角线上的2条腿在摆动中始终具有相同的摆动方式和相位，占空系数等于0.5.

衡量一种步态的好坏因素主要在于：在相同的稳态条件下，速度越快，消耗能量越少的步态就会相对优越.而对于本文，其所研究的机器人步态方式主要考虑重心单独调整方式的静态步行.所谓的重心单独调整静态步行是指在腿摆动过程中，机器人重心不发生变化，待4条腿全部处于支撑状态时，机器人重心再单独向前移动，其稳定性最高[10].在行走过程中为使步态达到理想的要求，还应考虑以下因素：①机器人整体运动灵活平稳，左右姿势协调；②在摆腿过程中，其腿各部件之间作用力以及足端与地面之间冲击力较小；③机身整体上下平稳，无明显的上下方向波动.四足机器人静态步行仿真运行步态如图5所示.

仿真结束后，得出机身质心以及各个足端运动随时间的运动曲线，如图6～10所示.

图6为机身质心X、Y、Z方向位移曲线，在机器人4条腿摆动过程中，其机身质心位移没有发生变化，机身保持不动，在2～3 s内机身前移过程中，机身质心前进200 mm，在侧向和竖直方向分别会产生微弱的偏移和振动，相对于机身本身的大小和高度，其影响较小，能保持直线平稳行走状态.

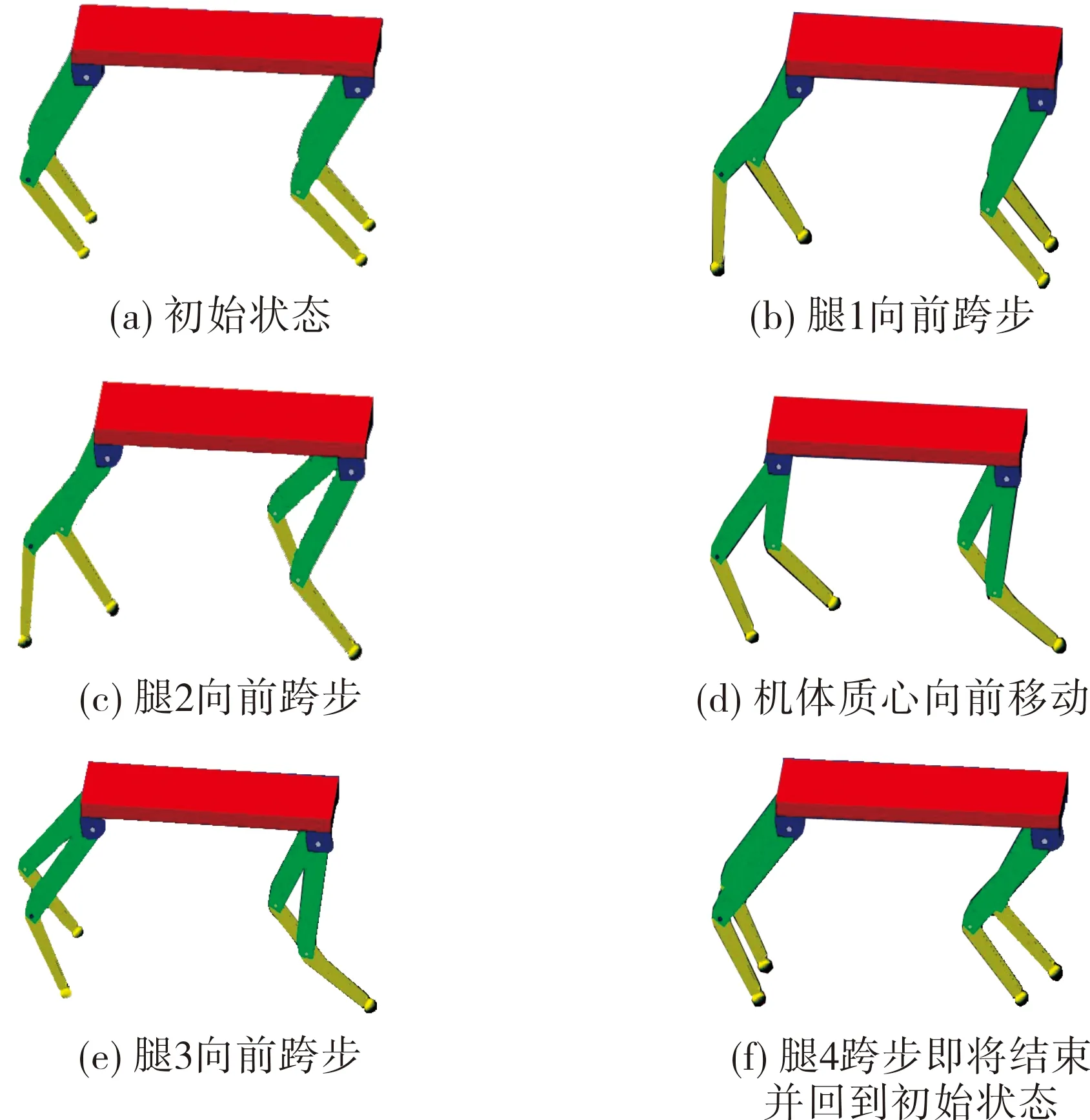
图5 四足机器人静态步行仿真运行步态

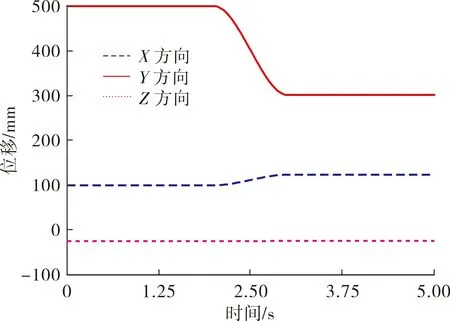
图6 机身质心位移曲线

图7为机身质心的速度和加速度曲线，在2～3 s机身运动过程中，其速度和加速度均匀增加和减少，整个运动比较平稳，能够遵循预先设计的运动轨迹要求，符合机器人的实际运动规律.

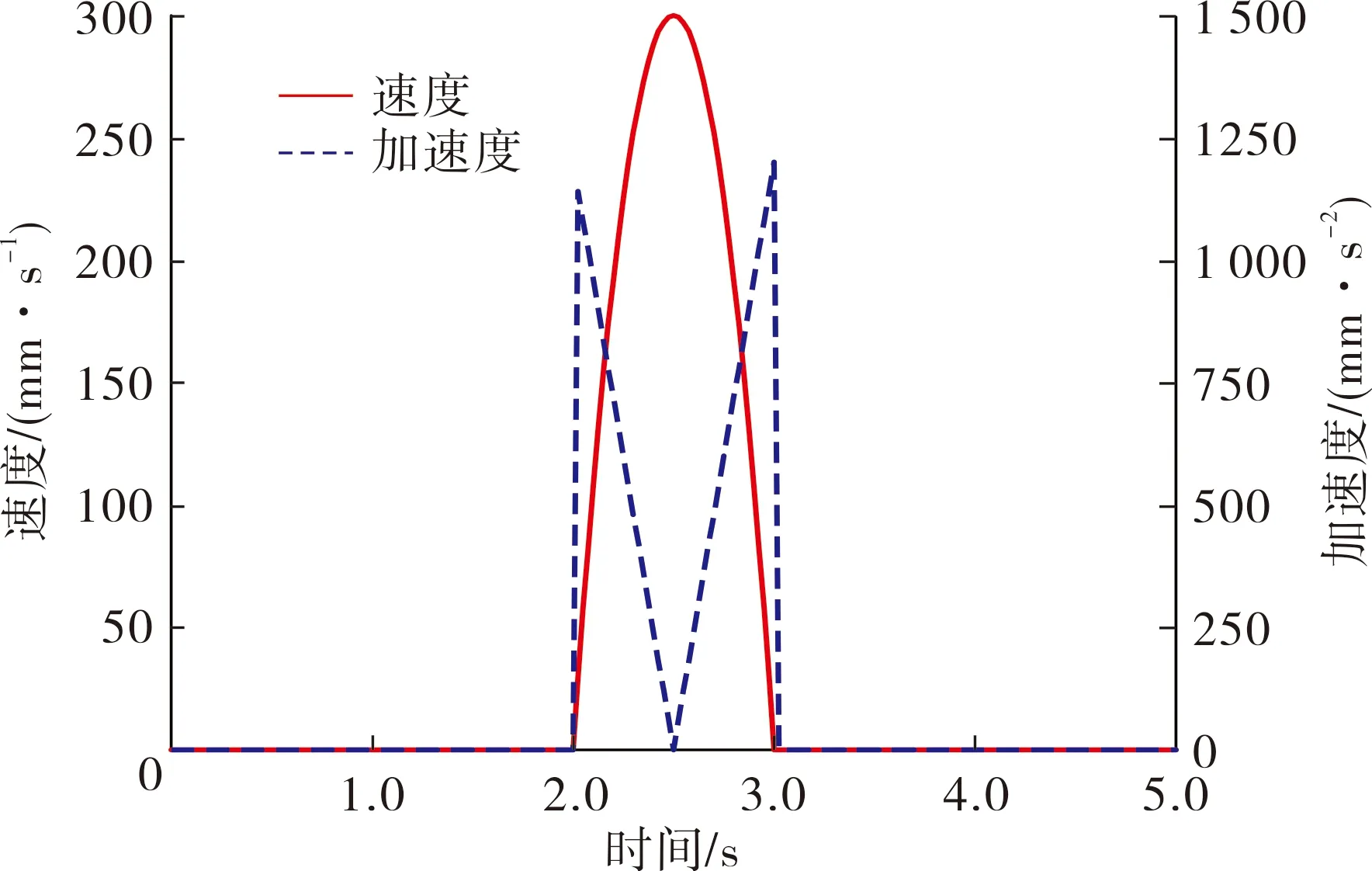
图7 机身质心速度及加速度变化曲线

图8～9分别为机器人各足端在竖直方向及前进方向上的位移曲线.各个足端在其运动过程中依次完成抬腿、跨越、落地动作，能够按照运动规律完成动作，且运动比较平稳协调，与实际的机器人足端运动轨迹和要求相符合.

图8 各足端Z轴竖直方向位移曲线

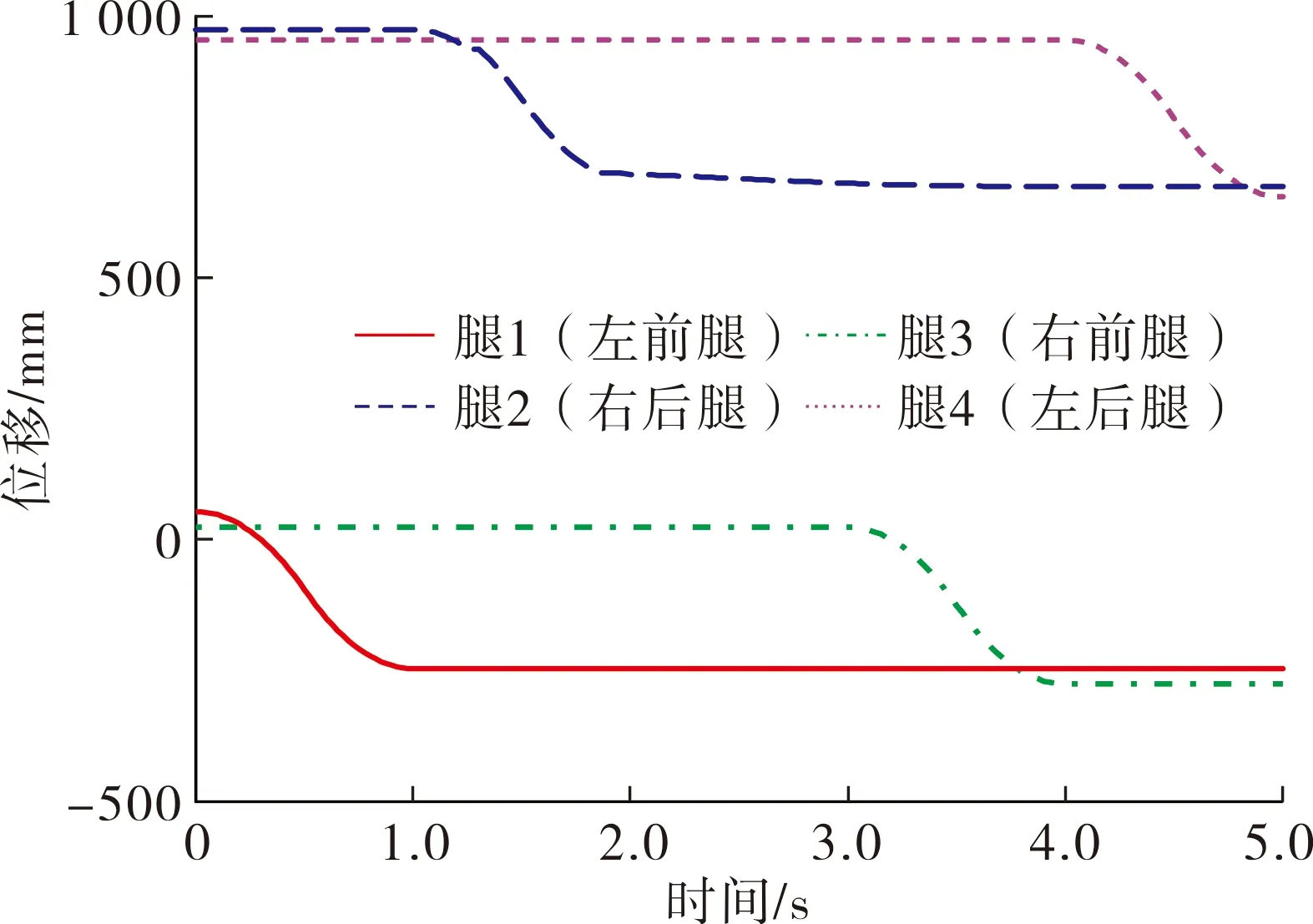
图9 各足端Y轴前进方向位移曲线

图10为机器人各足端的运动速度曲线，可以看出：由于各足端在落地时受到地面的冲击，会产生一定的竖直方向震荡，不过幅度不大，可通过在足端底部增加橡胶垫、在小腿上安装弹簧等措施来减少冲击和震荡.

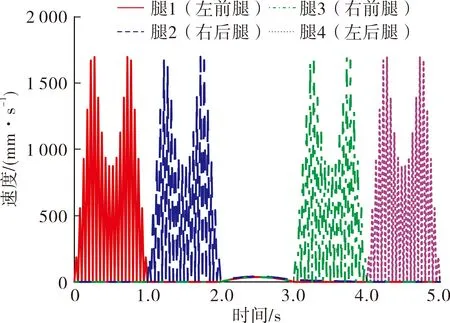
图10 各足端运动速度曲线

4 结语

本文通过对现有足式机器人运动方式和特性进行研究分析，并依据四足机器人的功能要求及腿机构的特性和缺陷，设计了一种模仿肌肉驱动的足式机器人新型腿机构.该腿机构采用油缸驱动，绳索滑轮牵引传动，膝关节和髋关节力矩变化小，承载能力稳定，足端运动空间大.通过ADAMS建立虚拟样机模型，以静态步行为设计基础，进行运动学仿真，以验证理论设计的正确性和合理性，为下一步详细的结构设计和样机设计奠定基础.虽然该研究成果具有一定的创新及使用价值，但是在液压系统设计以及液压元件与滑轮绳索牵引传动控制方面还有待问题解决，需要进一步的研究.