基于SVR的船舶操纵运动黑箱建模

卢冠宇， 姚建喜

(武汉理工大学 a. 高性能舰船技术教育部重点试验室；b. 船海与能源动力工程学院， 湖北 武汉 430063)

利用船舶操纵运动的数学模型进行计算机数值模拟是船舶操纵性预报最常用和最有效的方法之一。船舶操纵运动的数学建模分为机理建模和黑箱建模。机理建模基于确定的数学模型，常用的为Abkowitz整体式模型和分离式数学模型(Maneuvering Modeling Group, MMG)。对于机理建模，所使用模型中水动力导数的精度是影响其预报精度的关键。目前，获取水动力导数主要有约束模型试验方法、经验公式法、基于CFD(Computational Fluid Dynamics)的数值计算方法和系统辨识方法等4种方法。由于CFD的数值模拟耗费大量的计算资源，难以满足工程的应用需要，而系统辨识方法很好地弥补了其缺点。系统辨识用于船舶操纵性预报的过程属于有参数回归，回归得到的水动力导数具有较为明确的物理意义，LUO等[1]使用LS-SVM(Least Square-Support Vector Machine)对船舶操纵性进行有参数的预报，并讨论减缓参数漂移的方法；李腾飞[2]使用扩展卡尔曼滤波法对MMG模型中的部分参数进行辨识。然而，船舶操纵运动实际上是一个非常复杂的非线性系统，机理建模的参数漂移不能消除，且在多数情况下使用机理建模难以建立高精度的船舶操纵运动模型。使用黑箱建模的思想进行无参数回归，将水动力与运动参数进行非线性的黑箱映射，可避免出现在系统辨识过程中水动力导数的耦合现象，从而提高预报精度。对于实船运动，黑箱建模便于讨论Abkowitz模型外一些项的影响，例如已知高阶项和未知项，且可随着船舶运动建模理论的发展而对输入因素进行扩展。

随着机器学习和人工智能技术的发展，多种新的方法被应用在船舶操纵运动模型精度的改进上。HADDARA等[3]利用BP(Back Propagation)神经网络对非线性水动力导数项构建黑箱进而预报船舶水面运动；蔡韡等[4]训练径向基(Radial Basis Function, RBF)神经网络对船舶操纵运动进行预报；王雪刚等[5]使用LS-SVM在多组仿真数据下预报了四自由度船舶操纵运动，但未对核函数参数变化进行讨论；梅斌等[6]采用模型参考和随机森林模型对船舶操纵运动进行辨识建模；白伟伟等[7]运用一种基于全局最优的局部加权学习算法对船舶操纵运动进行黑箱建模；谢朔等[8]将多新息在线方法引入SVM辨识建模。SVM最早用于解决分类问题，显然运动预报属于回归问题，此时其形式为支持向量回归(Support Vector Regression, SVR)。

本文使用10°/10°、20°/20°Z形试验和35°回转试验的少量仿真数据进行样本重构，代入SVR黑箱模型进行训练，通过网格搜索交叉验证对核函数的选取以及参数的调整进行试验，用所构建的黑箱模型较为准确地预报10°/10°、20°/20°Z形运动和35°回转运动，验证了该黑箱模型的有效性；基于该模型泛化预报15°/15°Z形运动和15°、25°回转运动，将预报结果和仿真数据进行比对，验证SVR黑箱模型应用于船舶操纵运动具有良好的泛化性。

1 操纵运动方程

船舶三自由度操纵运动方程为

(1)

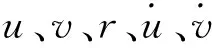
将船体所受水动力进行泰勒级数展开，即式(1)可表示为

(2)

式(2)中：Xu、Yv和Nv为水动力导数；Δu为关于初始纵向速度的变化量。

将式(2)中所有加速度项移至左边为

(3)

式(3)中：F1、F2、F3为关于运动参数u、v、r和δ的函数；等式左端除(角)加速度项外皆为常量，因此，各(角)加速度可表示为运动参数u、v、r和δ的函数，并将加速度项离散为差分形式

(4)

即：

(5)

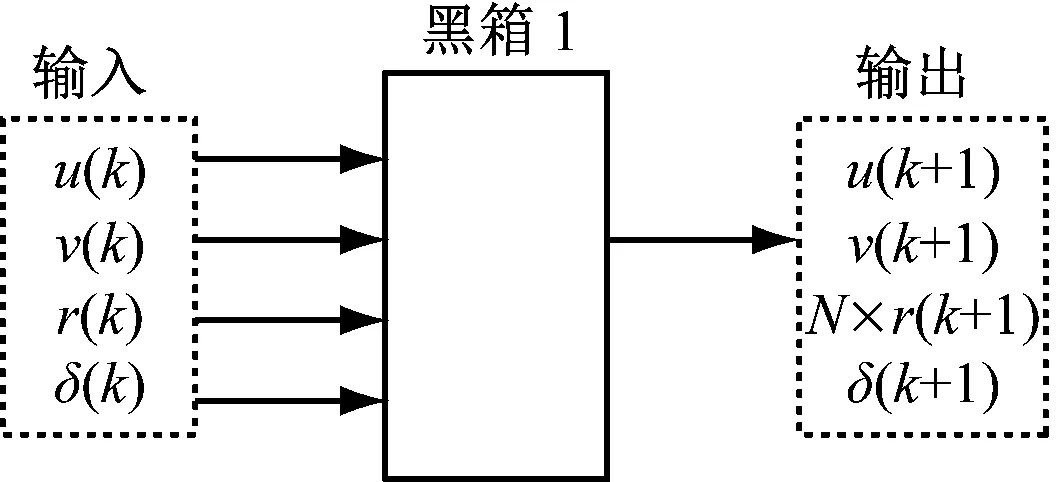
式(4)和式(5)中：k和k+1为当前时刻和下一时刻；g1、g2、g3为u、v、r和δ的非线性函数，可使用黑箱模型表示非线性函数，在这个黑箱系统中，输入{u(k),v(k),r(k),δ(k)}就可输出{u(k+1),v(k+1),r(k+1)}。

2 SVR和网格搜索

2.1 SVR原理

对于式(5)所反映的函数关系，使用SVR建立预测模型。给定训练样本集D={(xi,yi),i=1,2,3,…,n}，输入为多维变量x∈Rm，输出y∈R。此时多输入单输出(Multi Input and Single Output, MISO)系统模型为

yi=ωTxi+b

(6)

式(6)中：ω为权重向量；b为偏置值。

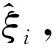
(7)

式(7)中：C为惩罚项系数。

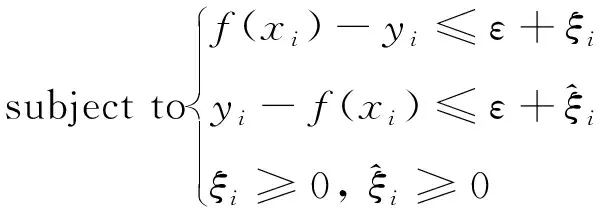
(8)

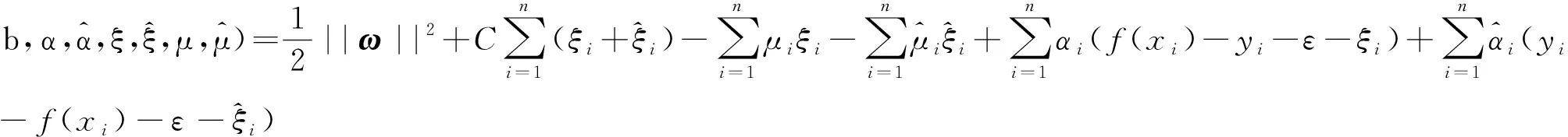
(9)

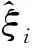
(10)

(11)

C=αi+μi

(12)

(13)

将式(10)～式(13)代入式(9)，得到SVR的对偶问题，有

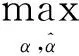
(14)

(15)

式(14)和式(15)为凸二次规划(QP)问题，存在最优解，常使用序列最小优化(Sequential Minimal Optimization, SMO)算法[10]进行求解，SMO算法的计算流程为

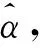
(16)

2.2 核函数与网格搜索交叉验证

在处理回归问题时只关注于结果的预测，并不关心过程中模型参数的大小。式(6)所反映的函数关系，明显是线性函数关系。在机器学习领域，当提取的特征与预测目标之间呈现非线性关系时，往往使用核函数来对其进行高维空间映射，将线性学习器拓展为非线性学习器，这种思想称为核方法。

常见的核函数有线性核函数、多项式核函数、RBF核函数和Sigmoid核函数等。对于船舶操纵运动模型，输入变量与输出变量之间明显是非线性关系，且线性核函数不包含可调参数，故先确定以使用多项式核函数和RBF核函数为佳。试验中多项式核函数的预测精度接近于RBF核函数，优先使用RBF核函数进行建模与网格搜索，而若RBF核函数不满足所设定精度阈值时，则使用多项式核函数继续寻优。以RBF核函数建立的SVR模型为

(17)

式(17)中：γ为核函数的尺度参数。

网格搜索法是一种遍历式的参数寻优方法，把指定区间划分网格，网格中每一个点都代表一种参数组合。将网格中包含的所有参数组合代入计算模型误差，比较误差大小，以得到最优参数组合。网格搜索交叉验证是指以K折交叉验证结果为寻优依据进行网格搜索。在网格搜索过程中，将数据集划分成K个子集，每次将其中1个子集作为测试集，剩余K-1个子集作为训练集进行训练；依次代入每一个网格中的参数组合，使用训练集构建模型，对测试集进行MSE计算；重复K次迭代，使每子集都曾作为测试集计算MSE，对K次MSE值求平均，作为最终评价网格搜索中参数组合优劣的依据，取交叉验证误差最小的参数组合作为最优结果。理论上，只要网格无限划分，最终所找到的参数组合即为全局最优。

本文使用网格搜索法对核函数参数进行寻优，步骤如下：

1) 将(0.1，10.1)视为γ的取值区间，取值区间均分为10等份，取其所有端点值(每次11个点值)代入核函数，使用10折交叉验证计算MSE，观察数据走向，取误差最小点，变量赋值为a。

2) 取p为已循环次数，以[a-0.5×10-p+1,a+0.5×10-p+1]为取值区间，均分为10等份，分别取其所有端点值代入核函数计算，使用10折交叉验证取得误差最小点，更新赋值为a。

3) 重复进行2)，直到MSE小于规定精度，取MSE最小值作为RBF核函数的γ参数。取q为最大循环次数，如循环q次仍不满足精度要求，分别使用三次和四次多项式核函数重复1)，直到MSE小于规定精度。

SVR黑箱建模总流程见图1。

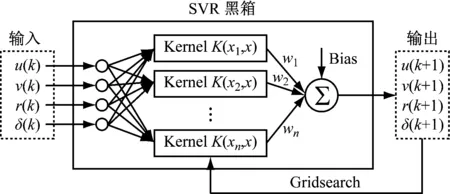
图1 SVR黑箱建模总流程

3 操纵运动预报

采用KVLCC2船型的CFD计算所得到的水动力导数，代入整体型操纵运动方程，对其三自由度的运动进行仿真，分别得到10°/10°，20°/20°Z形试验和35°回转试验的运动数据，迭代步长皆为0.1 s，其中Z形试验以4次转舵操纵为限，35°回转试验以3 000 s为限。将以上仿真所得4组数据汇总等距抽取1%(共694个样本)用作样本数据。仿真模型KVLCC2的主要参数见表1。

表1 仿真船型KVLCC2的主要参数

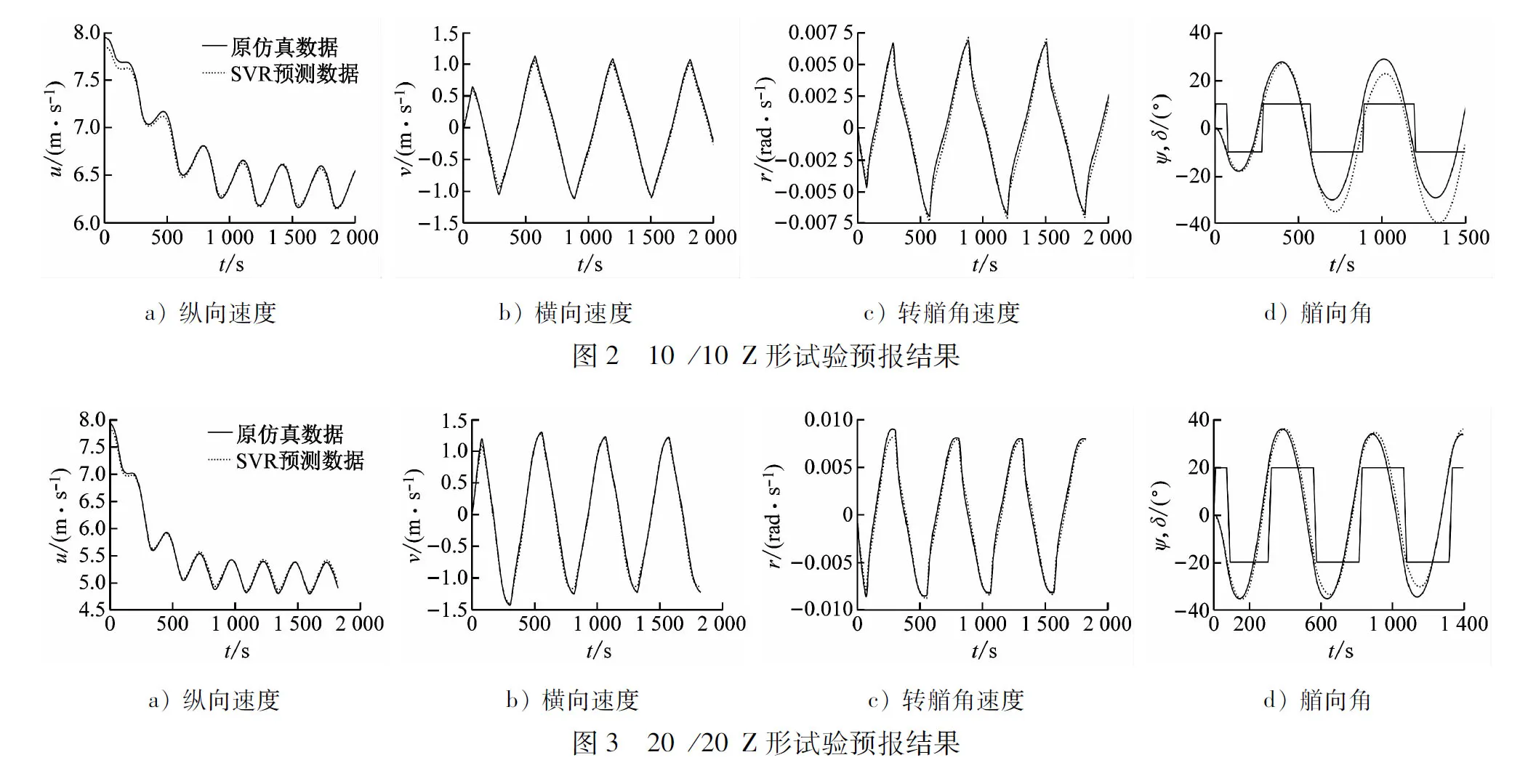
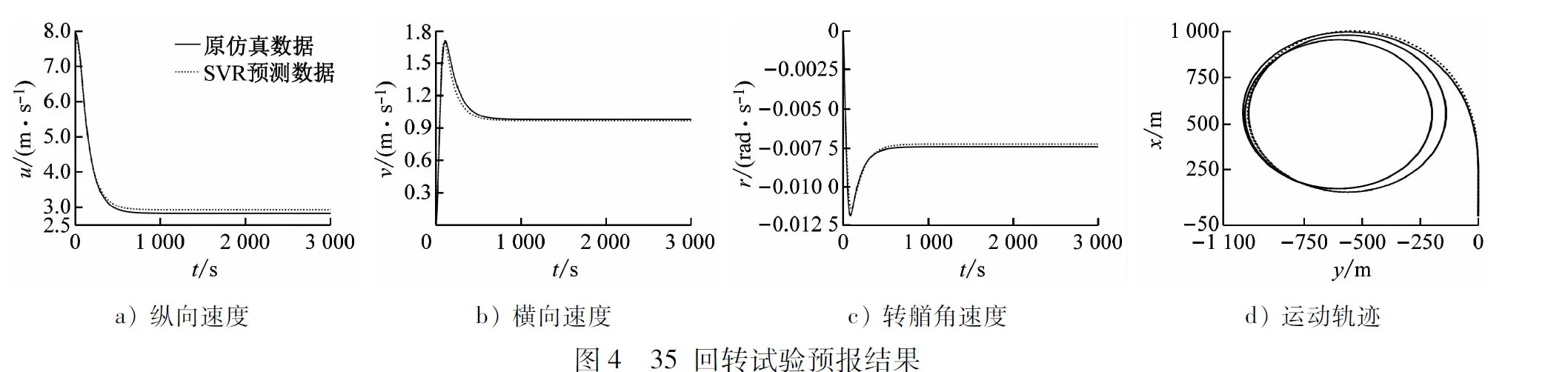
在仿真生成的无噪声数据中，松弛变量的惩罚项系数C对SVR结果几无影响，取C=106表示回归过程仅容许较小误差；取ε=0.1，基于网格搜索法对γ参数和对应核函数类型进行寻优，并使用10折交叉验证对应γ值所构建SVR黑箱模型的泛化性进行评估。在黑箱映射建立过程中，由于r量级较小，仅为u量级的万分之一，使损失函数变化的敏感程度低，针对r的样本输入进行构造处理(构造方法见第4节)。使用黑箱模型预报10°/10°、20°/20°Z形试验和35°回转试验的u、v、r，并通过以上预测速度值计算艏向角ψ与35°回转试验中的对地坐标x和y，见图2～图4。由图2～图4可知：本文建立的SVR黑箱模型可较为准确地预报船舶操纵运动。

4 样本构造与讨论

在黑箱映射建立过程中，由于r量级较小，仅为u量级的万分之一，使损失函数变化的敏感程度低，直接使用原始样本则无法构建r(k+1)关于自变量的映射关系，见图5c～图7c，需要针对r进行样本构造。本文使用的样本构造方法有两种：

1) 第一种(简称构造1)是仅对样本中r的因变量值扩大一定倍数处理，假设这个倍数为N，此时构建的映射反映的是N×r(k+1)关于原输入自变量的关系。在预报过程中，在黑箱映射后除以该倍数N就可得到r(k+1)的预测值。

2) 第二种(简称构造2)是对样本中r的自变量值和因变量值都扩大一定倍数，此时所构建映射反映的是N×r(k+1)关于输入自变量{u(k),v(k),N×r(k),δ(k)}的关系，预报得到的N×r(k+1)除以该倍数便可得到r(k+1)的预测值。两种样本构造的黑箱模型间的区别见图8。

分别使用构造1和构造2对船舶水面三自由度运动进行预报，见图5～图7。由图5～图7可知：两种构造对于u和v的预报精度相当，但对于r的预报精度不同。使用构造1对10°/10°、20°/20°Z形试验中r的预报更为精确，体现在ψ随时间的变化上，表明r的时历预报中误差的积累小，而构造2对r的预报会使ψ计算随时间不断积累更大的误差，导致数据偏离加大；对于35°回转试验，构造1对r的预报精度明显不及构造2的预报精度。因此，在第3节中，优先使用构造1进行预报，而仅针对35°回转试验中r的预报使用构造2。

5 网格搜索作用可视化

SVR黑箱模型对船舶操纵运动可实现在小样本下快速准确地预报。在网格搜索过程中，以35°回转试验的结果为例，见图9，核函数类型的选取以及核函数取不同的γ值对预报精度产生明显影响。系统筛选的寻优核函数类型和γ值及对应MSE见表2。

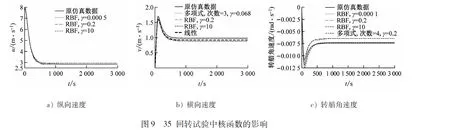
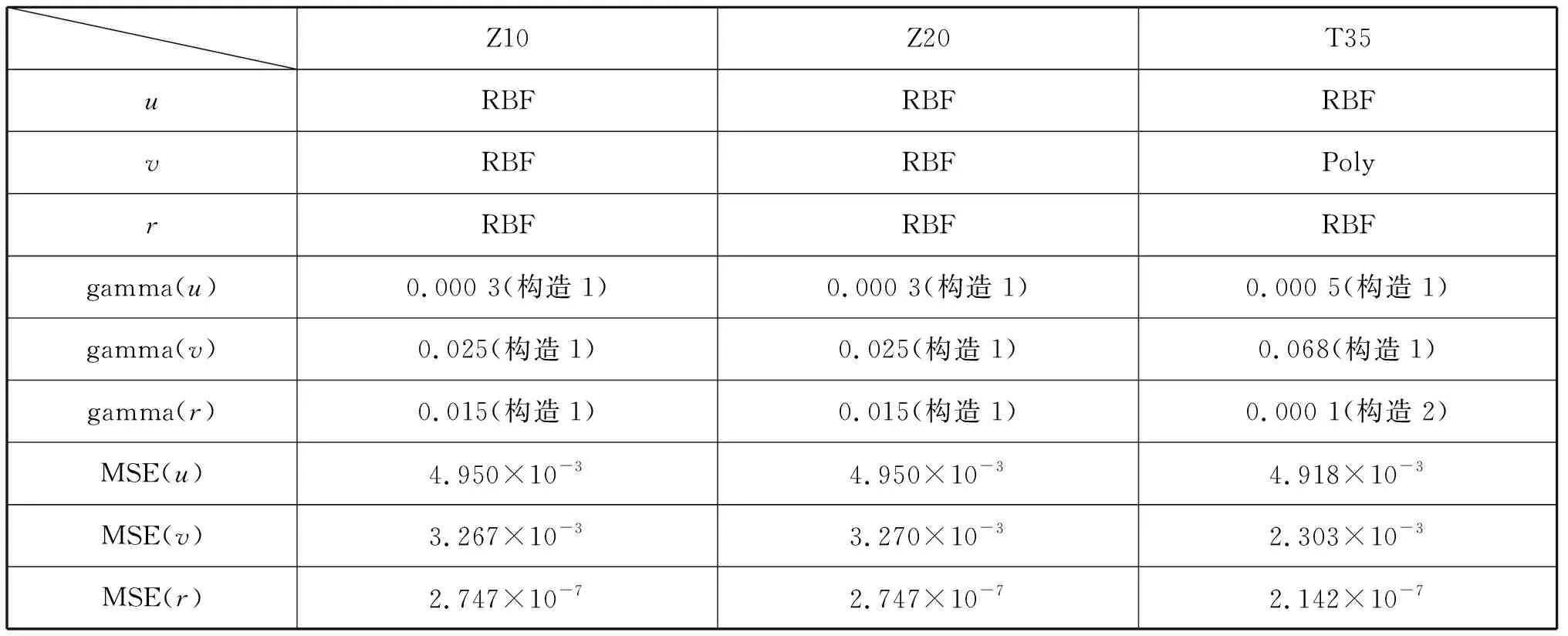
表2 寻优核函数类型、γ值及对应MSE

10°/10°、15°/15°、20°/20°Z形试验和15°、25°、35°回转试验的预报精度采用10折交叉验证的MSE来衡量，误差值越接近于0表示预测结果越准确如表2所示。

6 泛化性验证

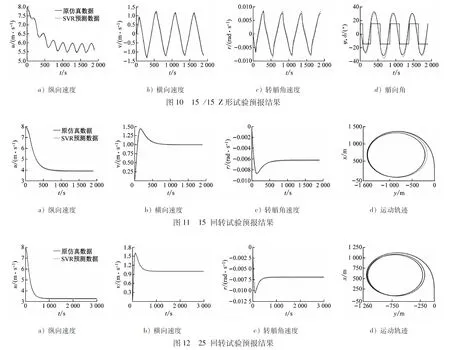
鉴于第3节中SVR黑箱模型已对10°/10°、20°/20°Z形试验和35°回转试验进行预报，现将该算法应用至15°Z形试验和15°、25°回转试验的预报，以验证SVR预报具有良好的泛化性。这里取倍数为100，对样本作以下处理：在对15°Z形试验的预报以及对15°、25°回转试验中的u、v的预报中，仅对样本中因变量的r(k+1)扩大100倍(构造1)；在预报15°、25°回转试验中的r时，对样本中自变量r(k)和因变量r(k+1)都扩大100倍(构造2)。用第3节所使用数据集建立SVR黑箱模型，使用网格搜索交叉验证对核函数的选取进行优化，预报了15°Z形试验和15°、25°回转试验的u、v和r，并通过以上预测速度值计算ψ与回转试验中的对地坐标x和y，见图10～图12。由图10～图12可知：基于SVR的黑箱预报方法具有良好的泛化性。

7 结束语

本文开展基于SVR的船舶操纵运动黑箱建模研究，结论如下：

1) 通过10°/10°、15°/15°、20°/20°Z形试验和15°、25°、35°回转试验预报结果与基于机理建模的仿真结果对比，验证所建立SVR黑箱模型的有效性，并具有良好的泛化性。

2) 对于SVR黑箱的训练样本，需对其进行样本构造，不同的样本构造会对结果精度产生影响，其影响主要体现在对r的预报。2种构造的区别是：一种仅对样本中因变量的r(k+1)扩大一定倍数(构造1)；另一种对样本中自变量r(k)和因变量r(k+1)都扩大一定倍数(构造2)。对r进行预报时，使用构造1对Z形试验中r的预报较为准确，而使用构造2则对回转试验中的r预报更为准确。

3) 不同的核函数类型与核函数参数的选取，对黑箱映射功能存在显著影响。RBF核函数具有较强的高维映射能力，一般使用RBF核函数建立模型就可满足精度要求。本文以多项式核函数作为备选，在使用RBF核函数难以达到精度阈值时用多项式核函数替代并搜索寻优，大大减少循环次数，缩短计算时间。

4) 用SVR黑箱建模的方法对船舶操纵运动进行预报时，对参与训练的操纵运动类型的预报不一定比泛化预报的运动类型更加准确，因为黑箱模型训练的过程是无记忆的，目的是为搭建对于输入输出损失最小的模型。例如本文抽取了10°/10°、20°/20°Z形试验和35°回转试验的694个样本对进行模型训练，对15°/15°Z形试验和15°、25°回转试验进行泛化性预报时部分结果具有更高的准确度。

5) 在Z形试验中，在对r的预报值随时间进行积分从而计算ψ时，会出现误差随时间不断积累的现象。分段训练样本、对船舶操纵运动进行在线预报等措施仍有提高预报精度的空间，值得下一步研究深入讨论。