基于改进SCGM(1,1)C模型的海上交通事故量预测

2021-03-12杜柏松艾万政胡林燕朱鹏飞

中国航海 2021年4期

杜柏松，艾万政，胡林燕，朱鹏飞

(浙江海洋大学船舶与海运学院，浙江舟山 316022)

海上交通事故量预测是海事安全评价和决策的基础，是海上安全管理部门总体控制水上交通安全的核心内容之一。[1]定量研究海上交通事故的变化趋势，对保障海上交通运输安全、提高海上交通安全管理水平具有重要的现实意义。目前，用于预测海上交通事故量的预测方法有支持向量机技术预测、BP(Back Propagation)神经网络预测和回声状态网络预测等预测方法[2-4],这些方法计算繁琐且需要大量的历史数据。由于灰色预测理论主要针对含有不确定因素，且具有一定变化趋势系统问题的预测；海上交通事故量具有随机性、不确定性等特点，且随着海上交通规范化和秩序化的发展，自开始统计以来总体呈现下降的趋势。因此，许多学者利用灰色理论对海上交通事故量进行预测研究。李云表等[5]利用GM(1,1)预测模型对舟山海域的海上交通事故量做了预测，其结果能反映海上交通事故量的变化趋势，但预测精度有待进一步提高。随着研究的深入，在灰色预测基础上建立许多灰色相关组合模型。虞盈等[6]在灰色预测的基础上，建立灰色马尔科夫组合模型，该组合模型能很好地克服数据的波动性；范中洲等[7]建立灰色BP神经网络组合预测模型，其结果比单一灰色预测和BP神经网络预测在预测精度和稳定方面更佳；徐东星等[8]等提出一种优化背景值和预测值残差的改进三参数灰色预测模型，取得良好的预测效果；陈昌源等[9]通过引入弱化算子序列对灰色预测的背景值进行优化，预测结果良好。以上灰色预测相关组合模型，在预测计算过程中依然存在预测过程不甚科学、计算过程复杂等特点，预测精度有待进一步提高；GM(1,1)模型是有偏差的预测模型，不能充分利用灰色系统的信息。[10]单因数系统云灰色预测模型(System Cloud erey Model, SCGM(1,1)C)是在GM(1,1)预测的基础上发展而来的，具有建模过程更加严谨，计算过程更简单、精度更高等特点[11]，该模型被广泛运用于航空、道路等交通领域[12-13]以及煤矿相关领域[14]的事故量预测研究中，取得良好的预测效果。

为更准确地完成预测研究，本文采用在交通领域事故量预测中运用比较广泛的SCGM(1,1)C预测模型，并通过相关算法对其进行多角度优化，构建改进的SCGM(1,1)C预测模型，以实现对海上交通事故量的高精度预测。

1 SCGM (1,1)c预测模型的建立

SCGM (1,1)C预测模型是灰色GM(1,1)预测模型的发展，其对原始数列的处理采用积分计算而非GM(1,1)预测模型的累加计算方式，即计算原理由梯形面积替代矩形面积，提高了预测精度。同时，相对于GM(1,1)预测模型，在确定模型参数时SCGM (1,1)C预测模型不需要大量的矩阵运算，且利用预测模型求取预测值时不需累减计算，预测计算过程得到简化。

SCGM (1,1)C预测模型建模过程如下：

设海上交通事故量样本数据序列为X(0)，有

X(0)={X(0)(1),X(0)(2)，…，X(0)(n)}

(1)

对样本序列X(0)进行积分生成变换，得X(0)={X(0)(1),X(0)(2)，…，X(0)(n)},有

(2)

而

X(1)(m)=0.5×[X(0)(m)+X(0)(m+1)]

(3)

设海上交通事故量积分样本序列X(0)与函数fr(k)=bea(k-1)-c满意趋势关联，用X(0)′的数据贴切拟合于fr(k)，计算可得到云灰色系数为

(4)

(5)

(6)

设X(0)(k)=b-c,U=ac，则有微分方程为

(7)

解该方程得

(8)

对X(0)′(k)进行还原处理，即可得到海上交通事故量的SCGM (1,1)C预测模型为

(9)

2 改进SCGM (1,1)C预测模型

系统SCGM (1,1)C虽然较灰色GM(1,1)预测模型在预测精度和运算过程上有一定提高，但该模型的基本原理是灰色预测，对于因不确定性因素造成的海上交通事故量的波动，该模型依然不能达到理想的预测精度。为提高模型的预测精度，对SCGM (1,1)C模型预测值提出修正。

2.1 马尔科夫理论修正预测值

样本值与SCGM (1,1)C模型预测值之差，称为预测残差，残差的分布情况可视为马尔科夫状态。[15]马尔科夫预测是通过计算各状态的转移概率来实现的，转移概率反映各状态的内在规律，其最显著的特点是无后效性，尤其适用具有较强波动性样本数据的预测。因此，将马尔科夫预测理论与SCGM (1,1)C模型结合起来，利用马尔科夫理论修正海上交通事故量预测值。

1) 计算海上交通事故量SCGM (1,1)C模型预测值的残差和相对误差分别为

(10)

(11)

2) 根据相对误差Q的分布情况，把其均分为i个数值区间，每个区间为一个预测状态，有

Ei=[Li,Ui],i=1,2,…,n

(12)

3) 构造转移概率矩阵，记由状态Ei转移到状态Ej发生nij次，而状态Ei在相对误差系列中出现ni次，则由Ei转移到状态Ej的状态转移概率为pij=nij/ni，可得1步状态转移概率矩阵为

(13)

P(n)=(P(1))n

(14)

式(14)为n步状态转移概率矩阵。

4) 通过计算状态转移概率并比较各个状态概率的大小，概率最大者为预测年份的状态。设预测年份状态为Ei=[Li,Ui]，取状态Ei的中间值Ii(白化系数λi=0.5)为修正参数，即

Ii=|0.5×(Li+Hi)|

(15)

则可得经过马尔科夫理论修正的马尔科夫SCGM (1,1)C预测模型为

(16)

当预测值大于样本值时，取“+”；当预测值小于样本值时，取“-”。

2.2 PSO二次修正预测值

由第2.1节马尔科夫理论修正SCGM (1,1)C预测值的式(15)可知：关于修正参数Ii的取值，人为选取了状态Ei的中间值，即λi=0.5，但在实际应用中，中间值并非一定是最优值，这样取值不科学且存在较大误差。[15]为合理的求解最优修正参数Ii，采用粒子群优化(Particle Swarm Optimization，PSO)算法对λ进行优化。 PSO算法是由Kennedy等提出的基于种群的优化算法，具有全局搜索能力强、参数少，计算过程便于MATLAP实现等优点，其基本算法为

vi(t+1)=wvi(t)+c1rand1(xpbesti-xi(t))+

c2rand2(xgbesti-xi(t))

(17)

xi(t+1)=xi(t)+vi(t+1)

(18)

式(17)和(18)中：xi为时刻t粒子的位置；vi为时刻t粒子的速度；xpbesti为粒子局部最优位置；xgbesti为粒子的全局最优位置；rand1、rand2为取值在(0,1)之间的随机数；ω为惯性系数；c1和c2为学习因数。

本研究设最优λ为粒子的最优位置x，以均方误差(Mean Square Error, MSE)表示为

(19)

MSE为适应度函数，通过MATLAP编程运算求解粒子的最优位置x值，即为最佳的λ。从而可得经过优化的修正参数为

(20)

将优化后的修正参数Ii代入式(15)即可得海上交通事故量的改进SCGM (1,1)C预测模型。

2.3 改进SCGM (1,1)C预测模型建模过程

梳理以上SCGM (1,1)C模型建模过程及对其进行的2次优化，可总结改进SCGM (1,1)C预测模型的建模流程，见图1。

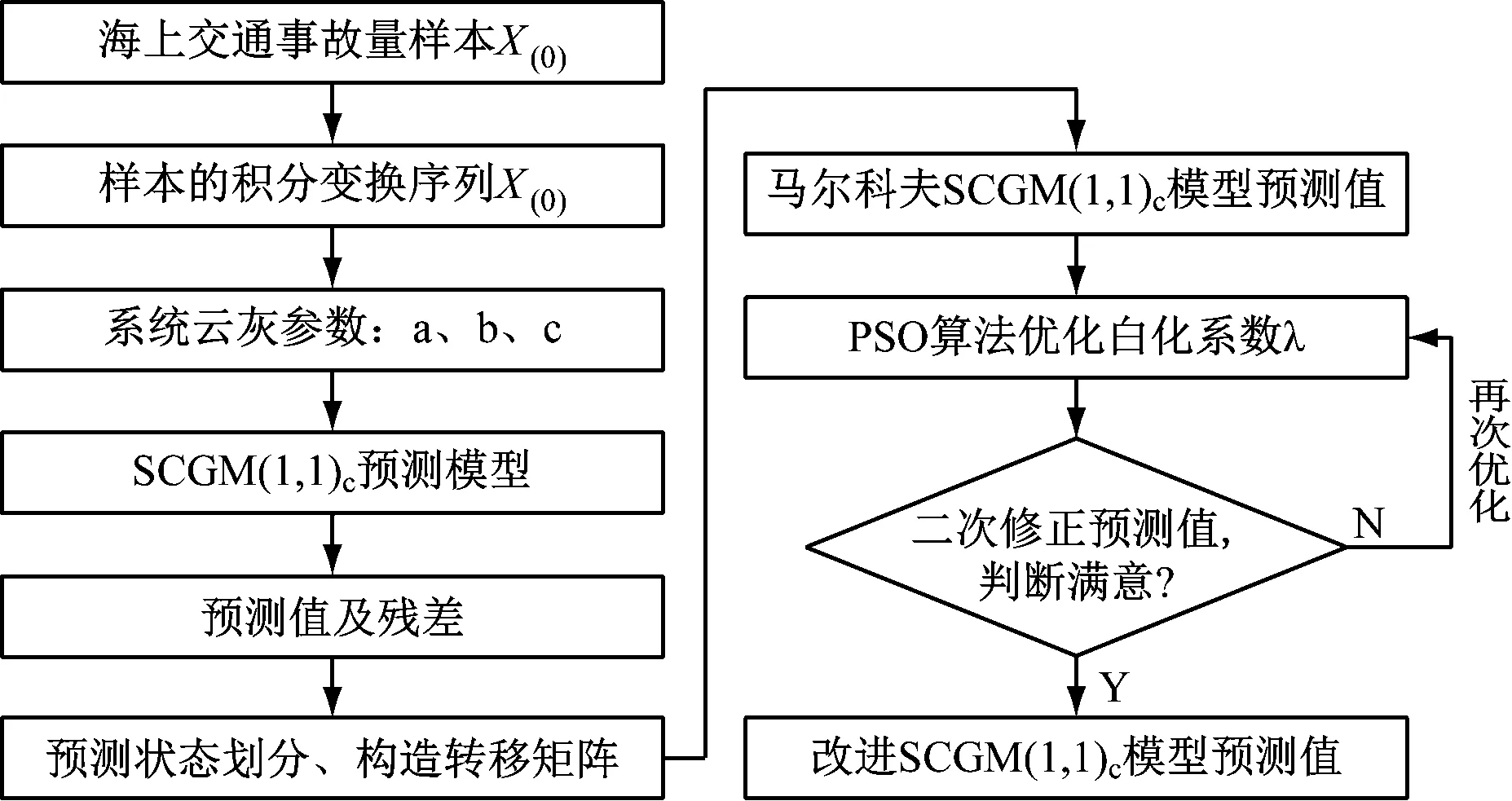
图1 改进SCGM(1,1)C预测模型的建模流程

2.4 模型检验

为验证改进SCGM(1,1)C模型的预测精度，应采取一定的检验方法对其进行检验。SCGM(1,1)C预测的原理为灰色预测，灰色预测常用的检验方法为残差校验和后验差校验[11]，因此，本文也选用这2种方法检验改进的预测模型。

2.4.1残差检验及指标

1) 最大绝对百分比误差(Absolute Percentage Error, APE)，体现模型预测值与样本数据的最大偏差，有

(21)

2) 平均相对误差(Mean Absolwte Percentage Error, MAPE)，体现不同模型对相同样本数据拟合程度的好坏，有

(22)

2.4.2后验差检验及指标

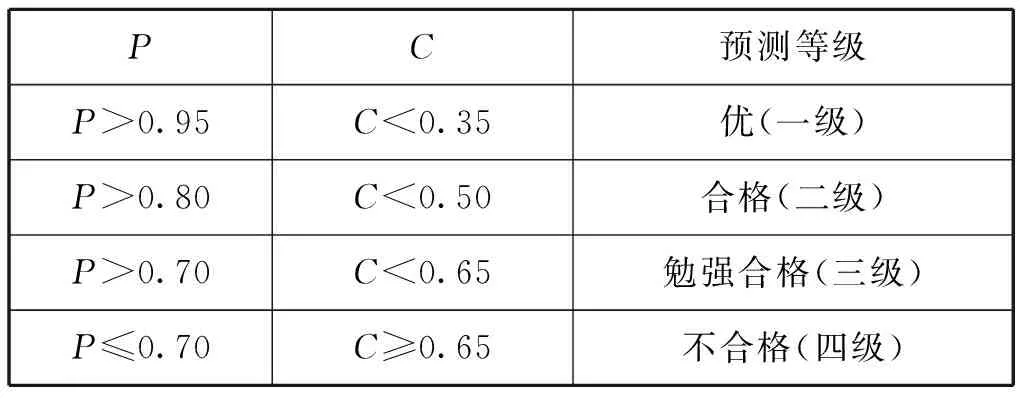
表1 预测模型等级划分表

3 实例分析

选取2004—2019年的海上交通事故量数据为试验对象(见表2)，对建立的模型进行实例验证和分析。根据改进SCGM(1,1)C预测模型的建模过程，以2004—2015数据为样本数据，通过建立SCGM(1,1)C预测模型及对其进行2次优化模型，分别计算相应的预测值并作拟合曲线，分析并判断改进模型的精度情况；同时，以文献[8]所建模型为比较对象，判断所建模型的准确性，并用所建改进模型对2016—2019年的数据进行实际预测，判断模型的可行性。

3.1 海上交通事故量的SCGM(1,1)C模型

取2004—2015年的海上交通事故量数据为样本数据X(0)，有

X(0)={562,532,440,420,342,358,331,298,270,262,260,212}

(23)

表2 2004—2019年海上交通事故量起

由式(2)～式(6)得SCGM(1,1)C模型灰参数：a=-0.094 3,b=-5 990.68,c=-5 970.92；代入式(8)得预测模型为

(24)

根据模型计算求解预测值，并计算e(k)和Q，见表3。3种预测模型拟合曲线图见图2。

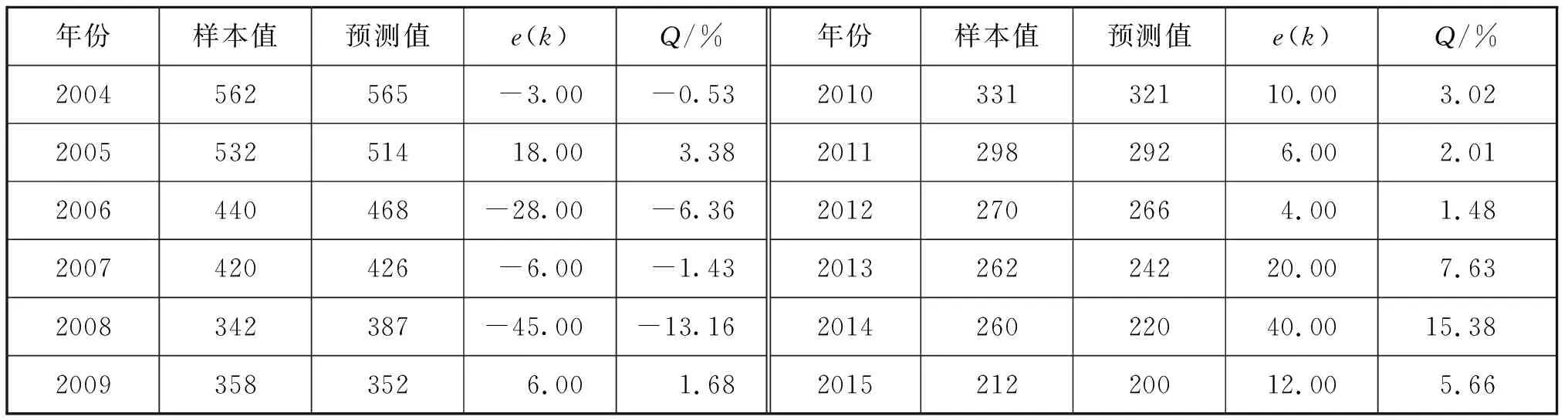
表3 SCGM(1,1)C模型预测结果起

由表3可知：2008年和2014年、2015年因样本值数据波动较大，预测产生较大的预测误差。由图2可知：预测值拟合曲线在2005—2009年和2013—2015年2个时间段背离明显。因此，SCGM(1,1)C模型有待改进。

3.2 马尔科夫理论修正预测值

为提高SCGM(1,1)C模型的预测精度，对该预测模型进行马尔科夫理论修正。由上文马尔科夫修正模型的建模过程，根据表3所列SCGM(1,1)C模型预测值相对误差的大小分布，把该模型预测值的情况划分为4个状态，见表4。

表4 SCGM(1,1)C模型预测值状态划分

由表4状态划分可得1步状态转移概率矩阵为

(25)

在确定各样本数据年份的预测状态和转移概率矩阵以后，即可利用马尔科夫理论对SCGM(1,1)C预测值进行修正：2004—2015年的预测值状态已知，因此，可直接通过式(15)和式(16)计算，修正的预测值见表5。对于2015及以后的预测值，首先利用SCGM(1,1)C模型求出预测值，然后以2011年、2012年、2013年和2014年作为马尔科夫预测状态的基础，由基础年份状态和多步转移概率矩阵得到累积概率并判断预测年份的状态，最后利用式(15)和式(16)计算。[16]

表5 不同惯性系数ω下改进SCGM(1,1)C预测值的MAEP

3.3 PSO算法二次修正预测值

为进一步提高SCGM(1,1)C预测值的精度，在马尔科夫理论修正预测值的基础上，使用PSO算法对其进行二次修正。根据建模过程及式(17)和式(18)，求解最优λ值。

本研究发现，黄油的固体脂肪含量比猪油高，有更好可塑性，同时与猪油相比，烘焙温度和循环加热次数的增加对黄油的酸价、过氧化值及多不饱和脂肪酸含量影响不显著（P＞0.05），这说明黄油在不同烘焙条件下具有良好的稳定性，但高温处理及多次加热会使黄油的单不饱和脂肪酸和饱和脂肪酸含量增多，因此，也应尽量避免黄油的重复利用并适当减少烘焙温度。

1) 首先设置PSO算法各参数，由表4可知：对 SCGM(1,1)C模型预测值的残差划分了4个状态，因此，取搜索维度D=4；由第2.2节所述，设最优λ(0≤λ≤1)为粒子更新位置x，所以取粒子更新位置xmax=1，xmin=0；PSO中种群粒子数和迭代次数越高，其优化效果就越好，但过高的粒子数和迭代次数会延长运算时间，因此，在保证精度效果和运算速度的情况下，取粒子数N=1 000,迭代次数k=1 000。[17]学习因数通常取c1=2、c2=2，且惯性系数0.6≤ω≤1.2时，PSO算法的搜索效率和搜索精度较高，且算法的收敛速度较快。[18]

2) 为取得最佳ω值，在以上各参数确定的情况下，分别取ω=0.6，0.7，…，1.2，编辑海上交通事故量粒子群优化MATLAP程序语言，并多次运行该程序，得到不同的λi，计算各ω值下的改进SCGM(1,1)C模型预测值的MAEP如表5所示。由表5可知：惯性系数为0.8时，改进模型预测值的平均误差最小，因此，取参数ω=0.8。

由上述参数运用MATLAP编程计算得：λ1=0.506 4；λ2=0.262 1；λ3=0.459 6；λ4=0.000 2，代入式(20)，再根据式(16)，可得经过PSO算法二次修正的预测值，即改进SCGM(1,1)C模型预测值，见表6。

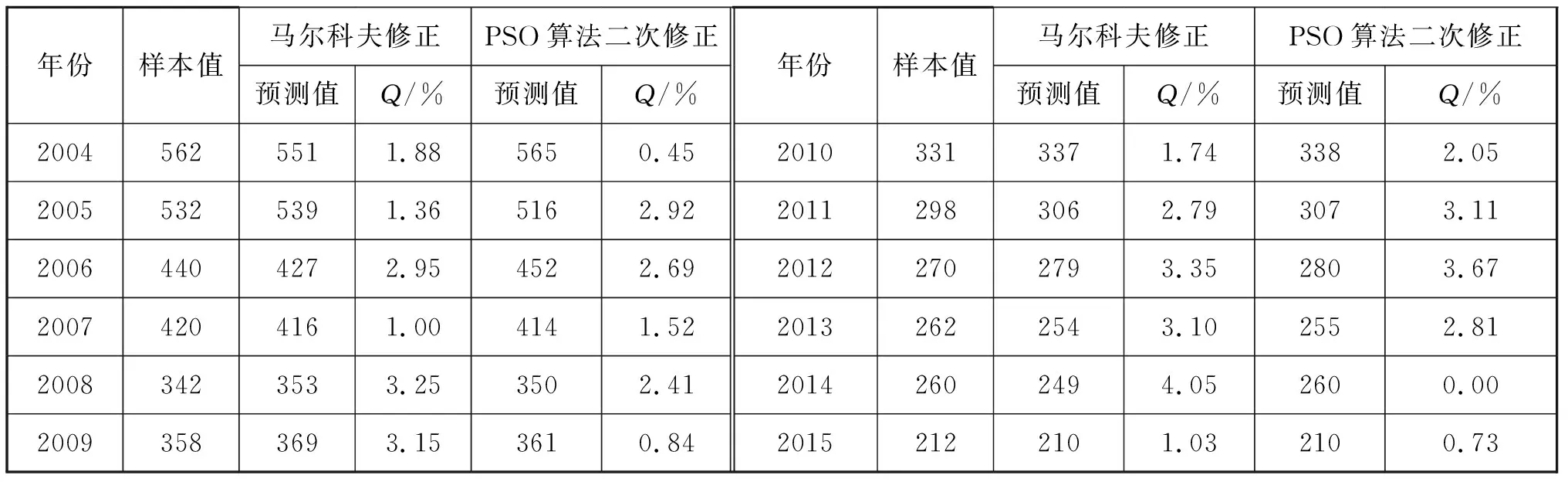
表6 改进SCGM(1,1)C模型预测值起

3.4 预测模型的精度分析

为验证SCGM(1,1)C预测模型及其改进模型的精度情况，计算各模型残差检验和后验差指标，见表7。

由表7和表1可知：新建的海上交通事故量SCGM(1,1)C预测模型达到“优”的一级标准，说明SCGM(1,1)C预测模型是适合与海上交通事故量的预测的；但该模型的残差指标MAEP=5.14%和APEmax=15.38%均较大，说明模型的精度有待提高。对模型进行马尔可夫理论修正后，修正模型的后验差指标C=0.09较单一模型的C=0.24有大幅度降低；同时，MAEP和APEmax两项指标值也大幅下降，说明经过一次修正后的模型预测精度有很大提高。分析经PSO算法优化二次修正的改进SCGM(1,1)C模型的精度情况，由表7可知：该模型相对于经马尔可夫修正模型的精度又有了进一步提高。

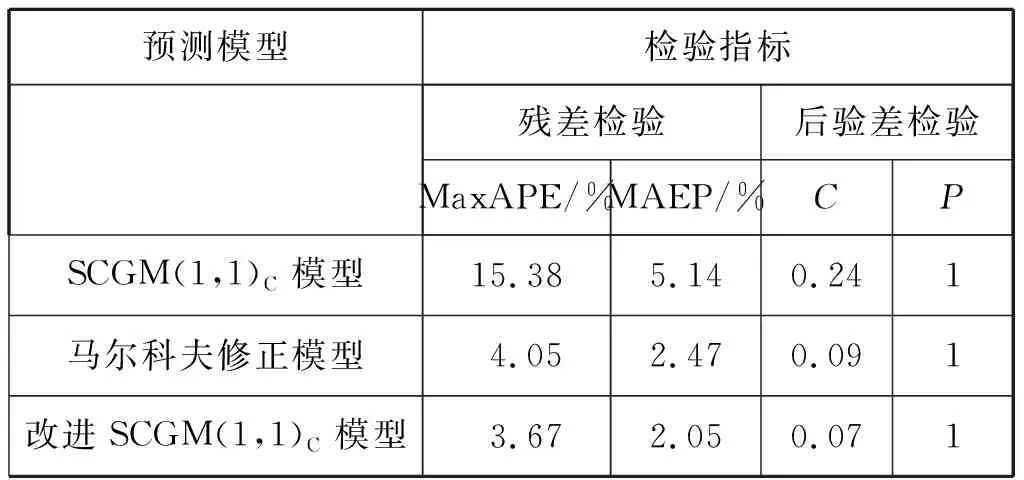
表7 SCGM(1,1)C模型和2个修正模型的预测精度比较

通过比对反映预测模型预测精度综合情况的MAEP指标：改进SCGM(1,1)C预测模型较马尔科夫修正模型的精度提高17.00%，较单一SCGM(1,1)C预测模型的精度提高60.12%；由图2可知：改进模型的拟合曲线与样本值曲线拟合度更高。综上所述，新建的改进SCGM(1,1)C模型是合理的。

为验证验证改进SCGM(1,1)C预测模型的实用性，用建立的模型对2016—2019海上交通事故量进行预测，结果见表8。由表8可知：2016年预测值精度满意，2017—2019年预测精度约维持在9%，精度一般，说明SCGM(1,1)C预测模型对短期预测有良好的预测效果，中长期预测精度有待提高。SCGM(1,1)C预测模型的理论基础是灰色预测，而短期预测精度较高，中长期预测精度一般也正是灰色预测的不足之处。[9]