结合Thevenin和PNGV模型的电池等效电路建模改进
2021-03-12汪贵芳王顺利于春梅
汪贵芳,王顺利,于春梅
(1.西南科技大学信息工程学院,四川 绵阳 621010;2.绵阳市产品质量监督检验所(国家电器安全质量监督检验中心),四川 绵阳 621010;3.四川华泰电气股份有限公司,四川 遂宁 629000)
0 引言
锂电池储能技术因其清洁高效、能量密度高、充放电性能好、响应速度快等诸多优点,已成为国内外储能技术的的重要发展对象[1]。与锂离子电池研究紧密相关的电池管理系统(battery management system,BMS)也得到了更多人的关注[2]。电池荷电状态(state of charge,SOC)是BMS中用于监测电池状态、避免电池过充过放的重要指标,其数值受电池电流、功率和温度等非线性因素的影响[3-4]。
电池模型反映了电池工作特性及其影响因素之间的关系,是SOC估计的基础。电池建模需要同时考虑电流、电压、内阻、温度、工作循环时间、SOC值等因素。所建立模型的精度直接影响SOC估计的精度。准确、简单的电池模型可以缩短电池管理系统的开发时间,使整个系统的开发过程更安全、更经济[5]。
目前,根据不同的研究机理和目标,通过试验分析建模方法建立的电池模型可分为电化学模型和等效电路模型。等效电路模型使用电阻器、电容器和电压源等电路元件形成模拟电池动态特性的电路,以表征电路的工作特性和描述电池的性能[6],具有更直观、易于操作、计算量适中、易于识别模型参数、适用于电路仿真试验等优点。因此,等效电路模型广泛用于实际工程应用中。
等效电路模型有助于使用电路和数学方法进行分析,使其成为广泛使用的电池模型。典型用例包括Rint模型、RC模型、Thevenin模型、PNGV模型。不同的电池模型具有不同的特性,它们在应用范围、模拟精度、使用条件和模型识别方法方面有很大差异。在实际生产中,模型的选择应考虑这些要求。
1 理论分析
1.1 电池建模
电池模型通过建立数学模型参数间的关系表达式,直观地表征电池的外部特性(电压、电流、温度等)与内部状态量(SOC、电阻、电动势等)的关系。锂电池等效建模是SOC估计的基础,其精度会直接影响SOC估计的准确性。常见的电池模型可划分为 4 类:电化学模型、热模型、耦合模型和性能模型[7]。锂电池在使用过程中会对外呈现出极化和滞后的效应。该效应与电路阻容模型所表现出的特性一致。因此,可以对电池进行等效电路建模。等效电路模型是电池性能模型的一种,使用电阻、电容和电压源等电路元件组成电路,模拟电池的动态特性。在实际应用中,应权衡现有等效电路模型的利弊,综合分析以选择合适的电路模型。
影响电池模型精度的因素主要有欧姆内阻、电池极化内阻、电池自放电特性、电池滞回特性等[8]。欧姆内阻是由电极材料、电解质、隔膜内阻和各部分接触电阻组成的电池内阻;极化内阻是在加载电流瞬间产生的阻碍电池中带电离子到达的趋势之和的电阻。极化电阻可分为电化学极化和浓差极化两部分。电化学极化是由电解质中的电化学反应引起的,浓差极化是由于反应物消耗引起电极表面得不到及时补充而导致的电极电势偏离通电前浓度平均值的现象。自放电特性自放电率是指电池在空载状态下自放电与额定容量之比。该特性用来表示电池容量的消耗率,通常用单位时间(月或年)电池容量减少的百分比表示。
1.2 HPPC试验
锂离子电池的混合脉冲功率特性(hybrid pulse power characterization,HPPC)试验通过分析电池在工作过程中工作特性获得电池模型参数[7]。该试验过程如下:首先对锂电池以1 C放电10 s;静置40 s左右,再以0.75 C充电10 s;在循环测试中,让锂电池在等间隔SOC点进行动力脉冲测试;选取SOC为0到1等间隔的点,相邻脉冲测试之间电池需要搁置1 h,使电池恢复到电化学和热平衡状态。整个试验主要由单个重复的充放电脉冲测试组成。HPPC试验流程如图1所示。

图1 HPPC试验流程图 Fig.1 Flowchart of HPPC experiment
HPPC试验选用容量为50 Ah、充电截止电压为4.2 V、放电截止电压为2.75 V、额定电压为3.7 V的三元锂电池。充放电设备是深圳雅科源科技提供的BTS200-100-104电池检测设备。试验环境温度为恒温20 ℃。在等间距SOC的HPPC试验之后,可以获得试验数据,并绘制电流和电压的曲线。选择其中一次循环的曲线进行参数辨识。一次HPPC试验数据曲线如图2所示。

图2 一次HPPC试验数据曲线 Fig.2 One HPPC test data curves
1.3 Thevenin模型及PNGV模型
Thevenin模型由内阻模型并联一个RC回路组成。其基本思想是用一个RC并联回路表征电池在使用过程中表现出的极化效应,在一定程度上弥补了内阻模型无法表征锂电池动态特性的缺点。其将电池复杂而抽象的动态响应问题抽象化,易于工程实现,是常用的模型之一[8]。Thevenin等效电路模型如图3所示。
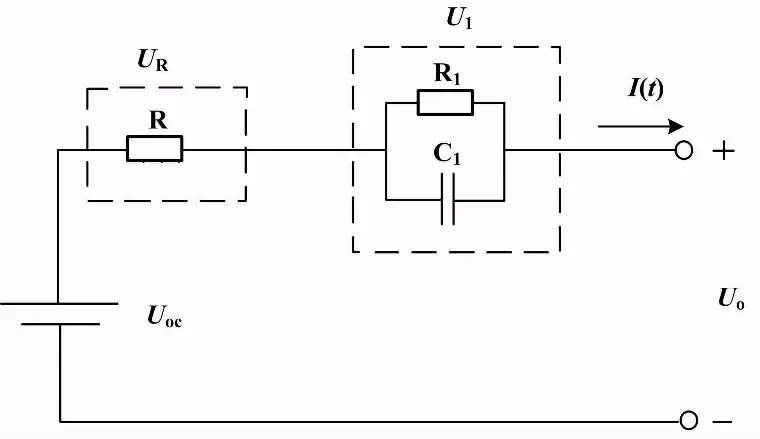
图3 Thevenin等效电路模型 Fig.3 Thevenin equivalent circuit model
图3中:Uoc为开路电压;Uo为端电压;R为欧姆内阻;UR为欧姆电压,为电池放电以及结束放电瞬间的电池压降效果。RC并联回路由极化电阻R1和极化电容C1组成,以表征锂电池的极化效应。其中:U1为极化电压。根据基尔霍夫斯基定律,分析所构建的Thevenin等效电路模型,可得到等效电路的电压和电流表达式为:
(1)
分析HPPC试验得到的图2及模型特征,可知电池的各参数计算表达式为:
(2)
(3)
(4)
式中:τ=R1×C为时间常数。
端电压计算如式(5)所示:
(5)
动力锂电池PNGV 模型是典型的非线性等效电路模型。该模型模拟瞬态响应过程的精度较高,适用于大电流、阶跃式、充放电较复杂的工况。为更好地体现三元动力锂电池在阶跃式充放电工况中的动态特性,对PNGV模型的极化电路进行了扩展,得到如图4所示的改进型PNGV等效电路模型。模型使用双RC电路代替原有的单RC电路。其中:RS和CS组成的并联电路时间常数较小,用于模拟电池在电流突变时电压快速变化的过程;RL和CL组成的并联电路时间常数较大,用于模拟电压缓慢稳定的过程。改进的PNGV电路模型可以更加贴切地表征电池的极化特性,并更好地模拟静态电路。

图4 改进型PNGV等效电路模型 Fig.4 Improved PNGV equivalent circuit model
改进后的模型端电压计算表达式如式(6)所示:
UL=R∞-(Ro×IL)-Up1-Up2-Ub
(6)
从图2中可以提取特征,计算得到模型参数:
(7)
对于双RC电路,可列出如下KVL和KCL方程。
UL=UOC(S)-i(t)-R0-US-UL
(8)
(9)
(10)
对两个串联的RC电路进行时域分析,可得RC网络的并联电路端电压为:
(11)
(12)
由模型的特征可知,t2~t3期间,电池端电压缓慢上升是极化电容对极化电阻放电的作用,是双RC回路的零输入响应。此阶段端电压的输出方程为:
(13)
为了将参数辨识简单化,将式(13)简化为系数方程:
UL=f-ae-ct-be-dt
(14)
式中:a、b、c、d、f是以式(13)方程为目标,采用Matlab对HPPC试验取得的数据进行双指数拟合所得到的系数。
(15)
改进型PNGV模型中的Cb,用于表征由于负载电流变化而导致的开路电压的变化。Cb的加入,使得模型可以很好地表征锂电池的稳态特性。
2 试验结果分析
2.1 参数辨识结果
根据上述试验步骤,对锂离子电池进行HPPC测试。试验端电压变化如图5所示。

图5 试验端电压变化图 Fig.5 Diagram of voltage variation at test end
Thevenin模型参数辨识结果如表1所示。

表1 Thevenin模型参数辨识结果 Tab.1 Parameter identification results of thevenin model
对试验数据进行双指数拟合后,得到的改进型PNGV模型参数辨识结果如表2所示。
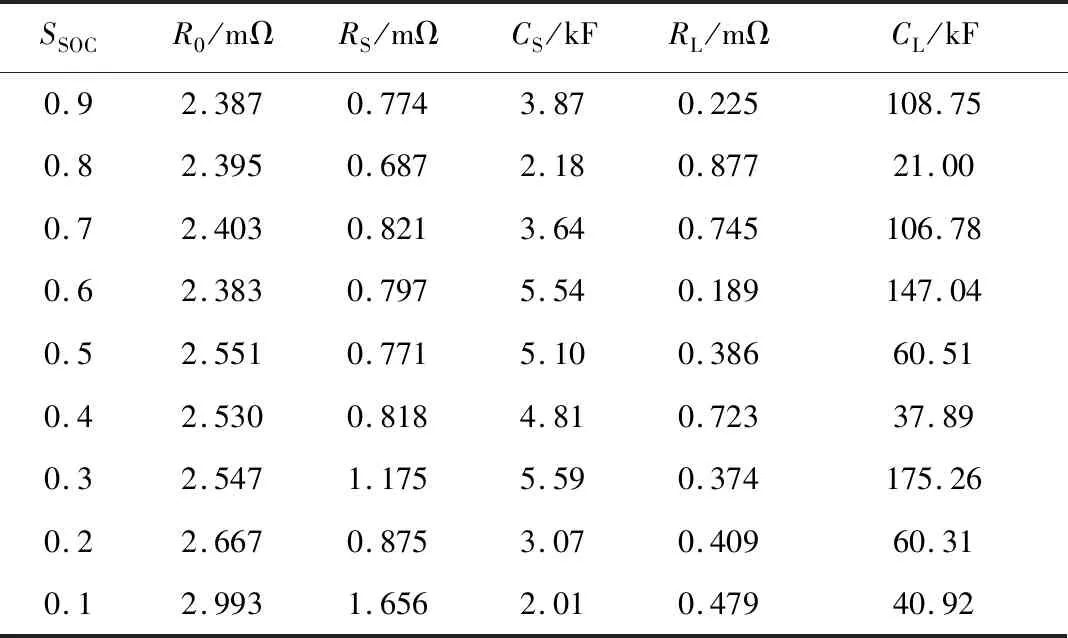
表2 改进型PNGV模型参数辨识结果 Tab.2 Parameter identification results of improved PNGV model
2.2 仿真结果
把通过HPPC试验得到的电流I、由参数辨识得到得各参数、开路电压Uoc、输出端电压UL和负载电流IL分别输入仿真模型的等效电路模块。输入参数中,除电流外的参数都是以SSOC为自变量的函数。其函数关系由参数辨识得到。根据安时积模块,可以得到SSOC的实时变化情况。将其连通到上述参数函数的输入端,就可得到对应电流输入不断变化的模型参数。整个模型的控制量是输入的电流值,响应量是模型的端电压,以此模拟锂电池的工作情况。
图6为试验和仿真得到的Thevenin模型端电压对比和误差曲线图。图7为改进型PNGV模型端电压对比和误差曲线图。

图6 Thevenin模型端电压对比和误差曲线 Fig.6 Terminal voltage comparison and error curves of Thevenin model
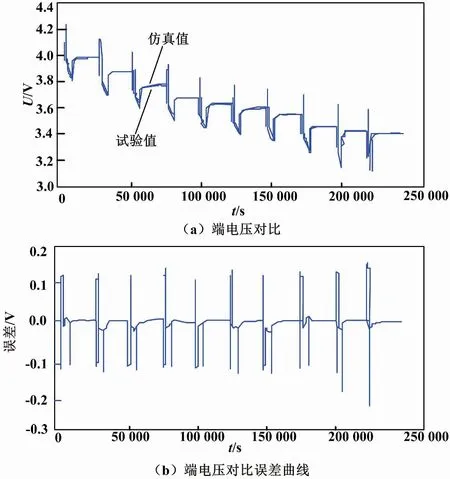
图7 改进型PNGV模型的端电压对比和误差曲线 Fig.7 Terminal voltage comparison and error curves of improved PNGV model
2.3 试验结果分析
①从图6和图7可以看出,两种模型的仿真输出电压与实际值吻合都比较良好,误差值也基本趋于稳定。这说明了两种等效电路模型的合理性与可行性,也证明了参数识别方法的可靠性。
②从图6(b)可以看出,Thevenin模型端电压比较曲线在整个试验过程没有过度发散,但在HPPC试验阶段出现较大的误差。其原因是电流的突然变化导致电池中化学反应的加剧,以及端电压的快速变化。此时,模型的最大误差不大于0.165 V。而锂电池的最大电压为4.2 V,所以其精度为96%。
③从图7(b)可以看出,改进型PNGV模型端电压比较曲线在整个试验过程没有巨大偏差。在SOC值的0~10%的范围发生误差的原因是:此时电池接近放电结束,内部电化学反应改变,电池模型中各参数值均发生很大变化。除此之外,端电压的仿真值与试验值基本保持一致,其误差总体小于0.055 V,占标称电压的0.13%,模型的精度超过98%。
3 结束语
通过对两种模型的误差曲线的比较和分析可以看出,Thevenin模型可以近似模拟出锂离子电池的外部特性,其精度为96%。但由于模型的阶数仅为一阶,在模拟锂离子电池的动态变化时得到的计算结果和实际电池的特性仍然有相对较大的错误。因此在Thevenin模型的基础上,改进的PNGV模型增加了一套RC电路,不仅考虑了电池的内阻,而且更好地解释了锂离子电池的极化效应能达到更深的拟合效应,其精度超过了98%。但是,改进的PNGV模型在某些地方仍然存在误差,并不能完全表达电池的所有外部特性。锂离子电池建模在自放电特性和滞后特性方面还有进一步改善的空间。
