一种极化码联合SC球形列表译码算法
2021-03-12陈发堂余永坤郑开放
陈发堂,陈 洋,余永坤,郑开放
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
2009年,基于信道极化定理(对于二进制离散无记忆信道,通过信道联合与信道分裂2个阶段,信道产生极化,其中一部分信道容量趋近于1;另一部分则趋近于0),Arikan提出一种新型信道编码:极化码。对信道容量趋近于1的部分信道输入信息比特,其余部分则输入冻结比特,从而在二进制对称信道下能逼近香农限[1]。因此,自从极化码的概念提出以来,在国际上引起了高度关注,于2016年,极化码已成为5G通信增强移动宽带(enhanced mobile broad band,eMBB)场景的控制信道编码方案。
极化码的经典译码方案为串行消除(successive cancellation,SC)译码算法[1],对信源比特逐位进行估计后删除其冗余的关联信息,并将估计值作为先验信息代入之后的译码运算,文献[2-3]提出了一种极化码SC译码码树节点分类分析方法,给出了一种简化SC译码算法。但在实际应用中,SC译码器译码性能有缺陷,较低密度奇偶校验码(low density parity check,LDPC)和Turbo码有一定的差距[4]。
为了提高极化码译码性能,文献[5]提出了一种性能更优的串行消除列表(successive cancellation list,SCL)译码算法,当列表尺寸LC足够大时,SCL译码算法的误码性能接近最大似然(maximum likelihood,ML)译码。通常,ML译码采用球形译码(sphere decoding,SD)算法实现[6-7],文献[8]提出了球形列表(list sphere decoding,LSD)算法,使用广度优先搜索(breadth-first search,BFS)以保持LD条最小欧氏距离候选路径,实质上是通过牺牲译码性能来降低复杂度。虽然SD算法的性能较其他算法更优,但是SD算法复杂度高,没有实际应用价值。文献[9]提出将SCL和LSD译码联合,而本文提出的极化码联合SC球形列表(joint successive cancellation sphere list,JSCSL)译码算法主要有3个优势:SCL译码和LSD译码2部分的计算复杂度更低;路径抉择方式不同,本文通过CRC校验的方式选择路径;中间分割点通过理论推导得出,以实现最优的并行译码。
在本文中,为了在计算复杂度和译码性能方面寻找一个折中方案,提出了JSCSL译码算法,即从前往后和从后往前2个方向同时执行SCL译码和LSD译码。仿真结果分析表明,与CA-SCL译码算法相比,JSCSL算法性能与其相近,但译码复杂度降低了40%~50%。
1 极化码概述
1.1 极化码编码
码长为N的极化码编码之前,首先将信道极化为N个二进制离散无记忆信道,通过信道联合和信道分裂2个阶段,部分信道的信道容量趋近于1;另一部分信道的信道容量趋近于0。然后趋近于1的部分信道传输信息比特,其余部分信道则传输冻结比特,从而逼近信道容量。
1.2 SCL译码
(1)
根据文献[1]中转移概率函数的递归公式,可以得到LLR的递推公式为
2tanh-1(tanh(α/2)×tanh(β/2))
(2)
为了降低SC译码器的运算量,文献[10-11]用最小近似法将LLR递推公式简化为
sign(α)sign(β)min(|α|,|β|)
(3)
(4)
在SC译码中,当前的比特估计值高度依赖之前的译码估计结果,如果前面某一位的结果出错,就会导致严重的错误传递,因此,一种基于SC译码的改进算法被提出,即SCL译码算法[3]。SCL译码算法使用BFS的方式,从仅允许选择“最好的一条路径进行下一步扩展”改为“最大允许选择最好的L条路径进行下一步扩展”,当搜索路径L=1时,SCL算法退化为SC算法。为了进一步提升译码性能,通过添加CRC校验的CA-SCL算法相应地被提出[12]。
1.3 LSD译码
SD算法模型为
(5)
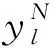
(6)
(6)式中,初始条件D(u(N+1))=0。因此,SD是找到具有最小欧氏距离的D(u(1))的叶子节点。SD译码中半径r2的设定极为关键,较小的半径值将导致修建所有的叶子节点,较大的半径值将导致较少的有效修剪,从而不必要地增加访问节点的数量,因此,多径SD树搜索被提出[8],采用多个不同半径值执行树搜索,半径r2的计算表达式为
(7)
(7)式中:α为r2的扩张步长;ω为扩张次数,初始值为1。当检测过程在执行第ω次树搜索时,候选解小于列表大小LS,若半径r2向外扩张,则执行(ω+1)次树搜索,直到最后得到LS条候选解,如图1。根据文献[8]得知,半径r2的最优扩张步长α为0.5。

图1 多径SD树搜索(LS=4)Fig.1 Multipath SD tree search (LS=4)
2 JSCSL译码算法
本文提出的JSCSL译码算法在译码复杂度上比CA-SCL译码算法更优,但与其译码性能接近。该算法的基本思想是对同一码字,同时执行SCL和LSD译码算法,待2种译码并行执行完毕后,联合其列表组合。这2种算法之间的共同点是都采用了BFS方式,不同点是译码路径抉择和译码顺序:SCL译码算法是通过计算LLR获得候选解,而LSD译码算法是通过计算与码字的欧氏距离获得候选解。
将长度为N的码字{u1,u2,…,uN},分割为2组{u1,u2,…,uM}和{uM,uM+1,…,uN},由于SCL逐次译码的特点,所以从u1到uM采用SCL译码算法,与此同时,从uN到uM+1采用LSD译码算法,从而得到2个译码列表,然后通过CRC校验的方式将2个译码列表联合,最终输出满足CRC校验的码字。图2展示了JSCSL译码流程,前M比特码字采用SCL(L=LC)译码得到LC条路径(Path1-PathLC),后(N-M)比特码字采用LSD(L=LD)译码得到LD条路径(Path1-PathLD),之后分别将LC条路径和LD条路径一一组合,待组合后的码字满足CRC校验,则输出码字结果。仿真结果分析表明,JSCSL译码算法在不损失译码性能的条件下,实现并行译码,降低译码复杂度。

图2 JSCSL译码方案Fig.2 JSCSL decoding scheme
本文中,计算分割点M是根据SCL和LSD的复杂度完成,目的是使2种并行执行的算法在相同时间内完成,以实现最优的算法复杂度。
首先是SCL复杂度的分析,根据SC译码算法的LLR递推公式(3),存在2种运算因子:Type A,f(α,β)≈sign(α)sign(β)min(|α|,|β|);Type B,g(α,β)=(-1)uα+β。“信息域”集合A的设定决定着Type A节点的个数N1和Type B节点的个数N2,对于列表排序采用冒泡排序算法。假设SACL,SMCL,SCCL为SCL译码过程中的加法次数,乘法次数和比较次数,分别表示为
(8)
LSD复杂度分析:根据(5)式,每一次i计算需要(N-i)次加法运算和(N-i+1)次乘法运算,ki为访问的第i个比特位置,假设SADL,SMDL,SCDL为LSD译码过程中加法次数,乘法次数和比较次数,分别表示为
(9)
通过上述SCL和LSD复杂度分析,为了达到最优的并行译码,让2部分独立译码在相同时间内完成,则M值计算式为
(10)
分割点M理论分析的正确性,通过第3节仿真分析得以验证。根据上述的理论分析得出JSCSL译码算法完整译码流程如下。
初始化:
分割点M=Point_cal(nodeSCL,nodeLSD);
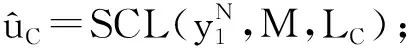
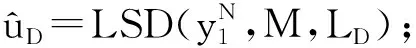
for i=1:LC
for j=1:LD
break;
end if
end for
end for
3 性能与复杂度分析
在本节中,对提出的JSCSL译码算法仿真结果进行分析,在加性高斯白噪声(additive white Gaussian noise,AWGN)信道下,采用的调制方式为正交相移键控(quadrature phase shift keying,QPSK)。
为了证明本文提出的JSCSL算法的性能,本节采取误帧率(frame error rate,FER)性能,以验证JSCSL算法给系统性能带来的提升。同时也对SC,LSD,SCL和CA-SCL算法进行了系统FER性能仿真和复杂度分析,以进一步验证JSCSL算法的性能。
分别对(256,128)型和(1 024,512)型极化码的FER性能仿真,并且将几种不同译码算法性能进行了仿真对比,如图3和图4。LSD,SCL和CA-SCL译码算法采用的搜索路径数相同(L=4),JSCSL译码算法中SCLpart和LSDpart采用的搜索路径分别为LC=4和LD=4,(256,128)极化码和(1 024,512),根据各自的“信息域”集合A,分别计算得出M1=153和M2=533,并且设定CRC校验码类型为CRC-24。
从图3和图4中可以看出,与SC,LSD和SCL算法相比,JSCSL译码算法可以显著提高译码器的FER性能,例如在Eb/N0=2.2 dB时,图3中分别约有7.2 dB,4.8 dB和2.7 dB的性能增益。随着码长的逐渐增加,给译码器带来的增益会随之增加。同样在Eb/N0=2.2 dB,图4中分别约有7.8 dB,5.7 dB和4 dB的性能增益。

图3 码长256时几种译码算法误帧率Fig.3 Frame error rate of several decodingalgorithms(256)

图4 码长1 024时几种译码算法误帧率Fig.4 Frame error rate of several decodingalgorithms(1 024)
通过对以上仿真结果分析得出,JSCSL算法译码器拥有显著的性能增益,但是随着码长的增加,JSCSL算法较CA-SCL算法的性能将有所下降,但下降趋势不明显。例如在Eb/N0=2.2 dB时,图3中JSCSL译码算法相对于CA-SCL译码算法约有0.2 dB,图4中约有0.4 dB的性能损失。虽然JSCSL译码算法相比于CA-SCL译码算法有所性能损失,但是JSCSL译码算法增加了译码的并行性,大大降低了译码复杂度。
在(256,128)和(1 024,512)极化码下,对JSCSL译码算法复杂性进行分析,并且与其他几种译码算法复杂性进行了对比,如表1和表2。在译码阶段,对加法器、乘法器和比较器3种运算器进行了次数的统计。

表1 码长256时几种译码算法运算器次数
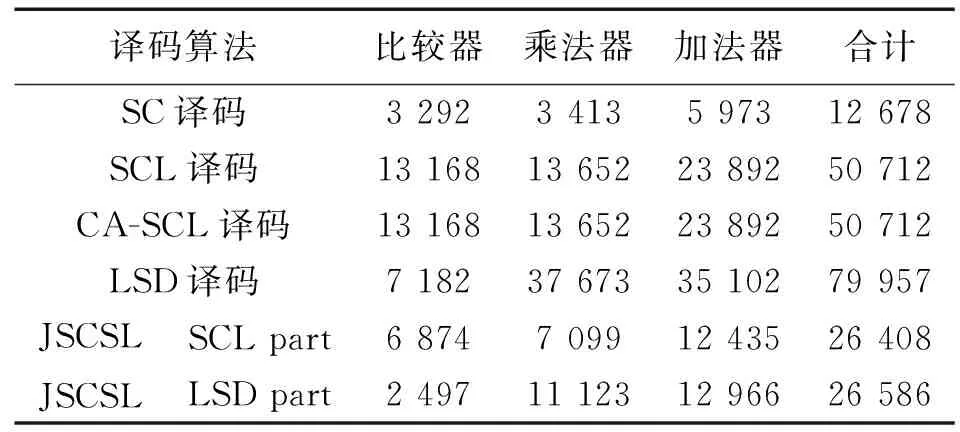
表2 码长1 024时几种译码算法运算器次数
从表1和表2中可以看出,将JSCSL译码算法复杂性分为独立的2部分:SCL part和LSD part,2部分使用运算器总和相差不大,从而也验证了第2节中对分割点M值的理论推导。表1中JSCSL译码复杂度相比于SCL译码,CA-SCL译码和LSD译码分别降低了约为40%,40%和62%,表2中JSCSL译码复杂度相比于SCL译码,CA-SCL译码和LSD译码分别降低了约为46%,46%和67%。
通过对JSCSL译码算法的仿真结果和计算复杂度分析可知,JSCSL译码算法相对于LSD和SCL算法在性能和复杂度方面都有很大的增益,缺点是JSCSL译码算法中添加了CRC校验码字,降低了译码有效性。与有效性相同的CA-SCL译码算法相比,在高信噪比条件下,虽然有0.2~0.3 dB的性能损失,但是在复杂度上降低了40%~50%。
4 结束语
本文提出的JSCSL算法是将码字分为2部分独立译码,增加译码并行性,从而达到降低译码复杂度的目的。通过对JSCSL译码算法的仿真结果和计算复杂度分析,JSCSL译码算法相比于LSD和SCL算法在性能和复杂度上都有很大的增益,但是损失了译码有效性。相比于CA-SCL译码算法,在信噪比高时,有轻微的性能损失,但在复杂度上降低了40%~50%,从而可以在复杂度和性能方面达到一个新的平衡。接下来需要研究的问题是,用硬件平台(例如FPGA)并行实现该算法。
