基于i-vector全局参数联合的说话人识别

杨明亮，龙 华，邵玉斌，杜庆治

(昆明理工大学 信息工程与自动化学院，昆明 650500)

0 引 言

利用声纹这一生物特征实现说话人的身份识别已成为身份认证的重要手段，目前这一技术已取得了一定成效并成功应用于国防安全、门禁安全、智能产品语音唤醒以及司法认证等领域。T. L. New等[1]提出利用隐马尔科夫模型(hidden Markov model，HMM)进行语音情感识别。R.C.Rose和D.A.Reynolds等又提出了高斯混合模型(Gaussian mixture model，GMM)，并由此延拓出相关的组合模型，如高斯混合深度神经网络模型[2](GMM-DNN)、高斯混合支持向量机模型[3](GMM-SVM)、通用背景高斯混合模型[4](GMM-UBM)等。再者，Dehak提出了i-vector说话人识别方法。

目前以GMM-UBM模型与i-vector模型为主流的说话人识别方法，D.A.Reynolds认为过去的说话人识别严重依赖于说话人的语音数据，希望通过训练大量无关说话人语音获得一个通用的说话人模型，再用少量的特定说话人语音数据对通用模型进行调整以得到说话人识别模型，即GMM-UBM。在GMM-UBM说话人识别模型中假定说话人的所有信息均存在于混合高斯函数的超矢量[5](Gaussian super vector，GSV))中。文献[6]提出了基于高斯均值超矢量的联合因子分析方法(joint factor analysis，JFA),认为均值超矢量中包含了说话差异和信道差异，故需要对说话人和信道进行分别建模从而去除信道干扰。然而Dehak认为信道因子中也会携带部分说话人的信息，在进行补偿的同时会损失一部分说话人信息，所以，Dehak[7]提出了全局差异空间模型(total variability model，TVM)，将说话人差异和信道差异作为一个整体进行建模，这种方法改善了JFA对训练语料的要求和计算复杂度高的问题。针对信道差异问题还提出了线性判别分析[8](liner discriminate analysis，LDA)、概率线性判别分析[9](probability liner discriminate analysis，PLDA)等信道补偿技术，其中以PLDA效果最佳。除此，也有如文献[10]所述方法对语音进行增强，以提高最终的识别性能。

i-vector将高斯均值超矢量通过全局差异空间矩阵映射为低维表示，消除了与说话人识别无关的信息[11](如信道空间、说话内容以及情感等)，相比GMM-UBM模型有了较大改进，但存在说话人特征的高维均值超矢量与低维隐空间映射关系并非简单的线性映射关系，PLDA对说话人模型的训练和评分[12]并未充分考虑数据匹配的问题。故本文提出了全局联合差异空间与联合信道补偿的PLDA的GPJ-IV说话人识别模型。

1 声纹特征识别方法

1.1 高斯超矢量方法

基于高斯超矢量的说话人识别由最初的GMM模型拓展成现在的GMM-UBM模型[13]，其前提假设为同一个人的同一维度特征在时间序列上近似满足高斯分布，故在此前提下便可利用C个k维高斯近似逼近真实分布(混合高斯数目越多其越逼近真实分布，但计算量也相应增大)，如(1)式为混合高斯表现形式

(1)

GMM-UBM模型其核心思想为首先通过训练大量说话人语音特征(不一定是训练人的语音)获取一个通用的说话人模型，其次利用少量的训练人语音特征在UBM基础上运用最大后验概率[14](maximum a posteriori，MAP)估计算法自适应得到各个说话人的模型，最后将测试人的音频特征通过UBM自适应得到说话人的超矢量特征，与训练好的说话人模型进行对比并给出评分，根据评分判决测试者身份。图1为GMM-UBM说话人识别流程。

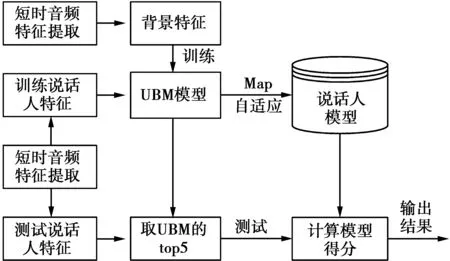
图1 GMM-UBM说话人识别流程Fig.1 GMM-UBM speaker recognition process

1.2 全局差异空间方法

Kenny[15]根据GMM-UBM模型提出了基于GSV的联合因子分析方法,其相关估计算法可参见文献[16]。Dehak针对联合因子分析方法进一步优化得到全局差异空间模型，将本征信道空间矩阵定义的信道空间看做为一个空间，它既包含了说话者之间的差异又包含了信道间的差异[17]。给定说话人的一段语音，与之对应的高斯均值超矢量可以定义为

Msh=m+Tw+ε

(2)

(2)式中：Msh为第s个人的第h条语音特征的GSV；m为通用背景模型(UBM)训练得到的高斯均值超矢量；Msh与m矩阵维度都为Ck×1；T为全局差异空间矩阵，又叫映射矩阵；w为全局差异空间因子，它的后验均值即为i-vector矢量，其先验地服从标准正态分布;ε为残差。由(2)式可知，最终需要的是w，但全局差异空间矩阵T未知情况下是无法获取w即i-vector矢量，因此，先求解T矩阵。为了消除原始的音频特征中的冗余信息，故首先计算背景数据库中每个说话人所对应的Baum-Welch统计量[17]用于接下来训练总体变化子空间矩阵T，其公式分别如下

(3)

(4)

(5)

(3)—(5)式中：Nc(s)，Fc(s)，Sc(s)分别为给定说话人s第c个高斯的零阶、一阶、二阶统计量；γt(c)表示t时刻对于给定特征向量yt第c个高斯的后验概率，其计算公式为

(6)

(6)式中：wc为UBM模型中第c个高斯的权重；pc(yt)有如下定义式

pc(yt)=N(yt|uc,δc)

(7)

在获取高斯混合模型的充分统计量后，首先随机初始化T矩阵，其次根据EM算法[18-19]进行迭代(一般迭代5～7次便可收敛)，其计算步骤如下。

E步骤：对给定说话人s的第h段语音，定义Ls为中间变量并有

Ls=I+TTΣ-1N(s)T

(8)

(8)式中，N(s)为Nc(s)的对角拼接Ck×Ck维矩阵，给定说话人s的语音特征矢量和参数集(T,Σ)条件下，总变化因子w的一阶二阶统计量分别为

E(ws)=Ls-1TTΣ-1F(s)

(9)

(10)

(9)—(10)式中：F(s)为Fc(s)的对角拼接Ck矢量，Σ分别为UBM模型的协方差矩阵。

M步骤：T矩阵迭代更新公式如下

(11)

进而更新UBM模型的协方差矩阵Σ(实验证明，只更新协方差而不更新均值效果更好些)

(12)

依据(3)—(12)式反复迭代至收敛即可。图2为基于全局差异空间的说话人识别流程。

图2 全局差异空间的说话人识别流程Fig.2 Speaker recognition process in global difference space

2 i-vector全局参数联合

2.1 全局联合声纹特征提取

基于因子分析理论的说话人识别可知，在整个说话人识别流程中，全局差异空间矩阵的求解至关重要，其矩阵相当于低维隐空间的基坐标并直接决定说话人特征的充分统计量在低维空间的表现形式，进而影响最终的说话人评分。理论上用足够多的说话人特征和足够多的迭代次数训练全局差异空间矩阵可获得理想的矩阵结果，但事实上我们通常无法获取充足的说话人特征，故针对此类问题本文提出联合全局差异空间建模进行声纹特征提取，图3为全局声纹特征提取流程。

步骤1分别对背景语音和训练语音进行短时特征提取。

步骤2将背景特征用于训练得到UBM模型。

步骤3将背景特征和训特征分别通过UBM模型自适应得到高斯超矢量GSV1和GSV2。

步骤4将GSV1通过随机初始化全局差异空间的T1矩阵,利用EM算法迭代几次即可获得收敛的T1矩阵。

步骤5将T1矩阵作为训练音频短时特征空间的初始化矩阵，通过几次EM算法迭代即可获得收敛的T2矩阵。

步骤6根据T1,T2隐空间分别提取训练特征的声纹特征iv1与iv2并进行全局联合得到新的声纹特征即

iv=q×iv1+(1-q)×iv2

(13)

(13)式中，iv为根据全局差异空间T1,T2以及加权系数q(实验测试所得经验值，取值过程在实验部分给出)计算出来的全局联合声纹特征，增强所提取特征的鲁棒性。

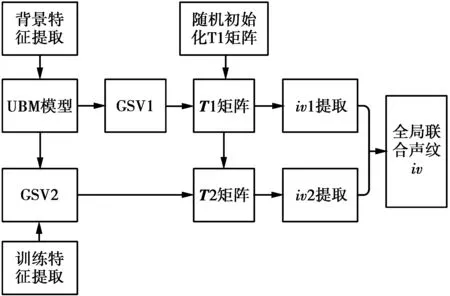
图3 全局声纹特征提取流程Fig.3 Global voiceprint feature extraction process

2.2 联合信道补偿

因为基于全局差异空间的说话人识别是将说话人和信道看为一个整体，这使得提取出的i-vector可能并非最优说话人特征，所以对于提取出的i-vector进行信道补偿是有必要的。众多信道补偿算法中PLDA效果最佳，但众多的i-vector模型中直接利用背景数据训练得到PLDA模型用于最终的似然评分中势必造成测试数据与已训练模型不匹配的问题，其PLDA模型表达式为

xij=u+Fhi+Gwij+εij

(14)

(14)式中：xij为i-vector矢量；u为i-vector的训练均值；F为用于描述说话人特征的说话人空间；hi为说话人空间对应的说话人因子；G为用于描述信道特征的信道空间；wij为信道空间对应的信道因子；εij为残差因子。hi与wij服从N(0,I)分布。(14)式用信道和说话人刻画了i-vector，但实际中我们只关心说话人之间的类间特征，不关心同一说话人不同音频段的类内特征，故可得简化的PLDA表达式

xij=u+Fhi+εij

(15)

(15)式中：h服从N(0,1)；ε服从N(0,Σ)分布(Σ为数据的协方差)，由此PLDA简化成了θ={u,F,Σ}参数估计，初始化参数后使用EM算法迭代几次即可获得收敛数值的参数。

为了尽可能使最终的测试数据与训练模型相匹配，这里引入全局PLDA参数联合，即

(16)

PLDA.u=(1-λ)×PLDA1.u+λ×PLDA2.u

(17)

PLDA.Σ=(1-λ)×PLDA1.Σ+

λ×PLDA2.Σ

(18)

(16)—(18)式中：λ表示依据背景特征数据和训练特征数据量的比值计算权值系数(可根据实际情况适当调参)；N1为背景语音特征数据量；N2为训练语音特征数据量；roundn表示四舍五入取值；a表示保留的小数位数；PLDA1与PLDA2分别为背景数据与训练数据训练得到的PLDA结构体。

3 实验设计与结果分析

3.1 实验设置

实验环境配置如表1。

表1 实验环境配置

本实验中为了测试不同语种以及方言对于说话人识别的影响，实验所采用的数据为TIMIT语音库、THCHS30语音库、2018方言种类识别AI挑战赛语音库(dialect recognition contest，DRC)3种，语音采样率为fs=16 000 Hz，单通道的wav音频文件，每句语音时长为4～7 s左右。在训练通用背景模型中采用了大量TIMIT与DRC数据库中的语音，而对于THCHS30语音库中的语音并未加入，以便分析语种是否影响说话人识别。其中，TIMIT语音库包含美国8个地区630个说话人语音，每人10句英语语音；THCHS30语音库包含20个来自中国各地的说话人语音，每人10句普通话；DRC语音库包含中国10个方言地区的350个说话人，每人10句中国地区方言；运用TIMIT语音库中的462个说话人(女性140人，男性324人，每人10句)、DRC语音库中300个说话人(女性150人，男性150人，每人10句)组建的包含762个说话人7 620句语音的语音库分别训练UBM模型和全局差异空间矩阵T1。实验训练数据包含TIMIT语音库中的168个说话人(女性52人，男性114人，每人9句)、THCHS30语音库中20个说话人(女性18人，男性2人，每人9句)、DRC语音库中50个说话人(女性30人，男性20人，每人9句)构建的语音库用于训练全局差异空间矩阵T2以及说话人模型，剩下238人每人一句的语音用于测试。

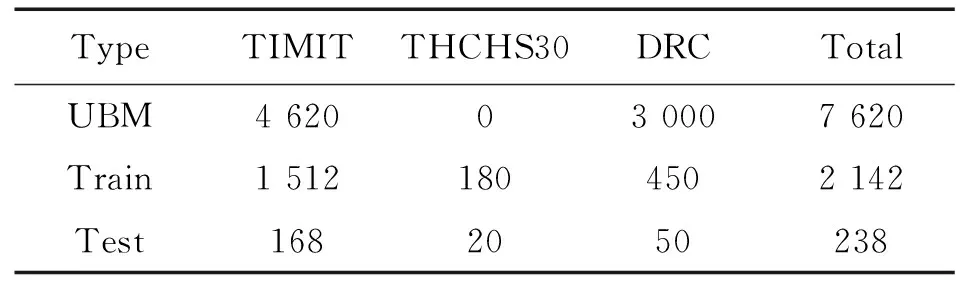
表2 语音库的分配设置

本文实验流程包括如下4部分。

1)语音预处理。对原始语音进行端点检测(因为说话人识别跟说话内容、情感、语速等参量无关，本文采用谱熵法端点检测，实验测试效果比双门限端点检测方法效果好)；对端点检测后的语音进行预加重(对语音的高频部分进行加重，去除口唇辐射的影响，增加语音的高频分辨率，本文设置的预加重因子为0.935)；分帧(本实验帧长为512个数据点、帧步长为256个数据点)。

2)特征提取。实验采用的音频特征类型有36维的梅尔倒谱系数(Mel frequency cepstral coefficents，MFCC)特征参数(其中包括12维倒谱与12的一阶和二阶倒谱)、24维的线谱对(line spectrum pair，LSP)特征参数、音频特征组(audio feature set，AFS)特征参数(包括短时能量、短时平均幅度差函数、帧基音周期、频谱质心、频谱带宽、频谱差分幅度、以及第1、第2、第3共振峰9个参数组成)。

3)模型训练。实验搭建了联合声纹特征iv、联合信道补偿PLDA以及IV-GPC模型分别进行训练，同时选取目前最为主流的2类说话人识别模型作为对比即GMM-UBM模型与i-vector模型。模型中相关混合高斯数目均设置为32。

4)说话人测试。将238个说话人的语音特征分别送入已训练好的238说话人模型进行238×238次评分测试，评分最高的说话人模型作为该个说话人的识别结果。

本文所采用的性能评价指标为等错误率(equal error rate，EER)与最小检测代价准则(minimum detection cost function 2010, DCF10)[19],其值越小代表性能越好。最小检测代价函数计算公式为

DCF=CFREFRPtarget+CFAEFA(1-Ptarget)

(19)

(19)式中：CFR与CFA分别为错误拒绝率EFR和错误接受率EFA的惩罚系数；Ptarget，(1-Ptarget)分别为真实说话测试和冒充测试的先验概率，这里参数采用NIST SRE2010设定的CFR=1，CFA=1，Ptarget=0.001参数。

因为Mindcf不仅考虑错拒绝和错误接收的不同代价，还充分考虑到测试情况的先验概率，在对模型性能评价上Mindcf比EER更合理，故依据Mindcf10实验值选取(13)式中的全局差异空间的权值系数q。

表3为MFCC特征对于6组实验，q为0.3时，Mindcf10取得最小值；MFCC+LSP特征相对应的Mindcf10取得最小值时，q为0.2；MFCC+LSP+ASF对应的Mindcf10取得最小值时，q为0.4；不同的特征其模型性能所对应的权值大小有细微不同，为了实验仿真测试统一，下述所对于全局差异空间权值q均取0.3。

表3 全局差异空间的权值系数选定

3.2 实验测试

本实验共设计了3类不同组合特征的实验，每类实验又分为5个不同说话人识别模型的对比实验，其中联合PLDA模型为i-vector信道自适应补偿模型，联合iv模型为i-vector基于全局联合空间提取的声纹特征识别模型，GPJ-IV为本文所提出i-vector全局参数联合的说话人识别模型。表4，表5，表6分别为不同特征组合以及在不同说话人识别模型上的性能测试与仿真时间对比测试。

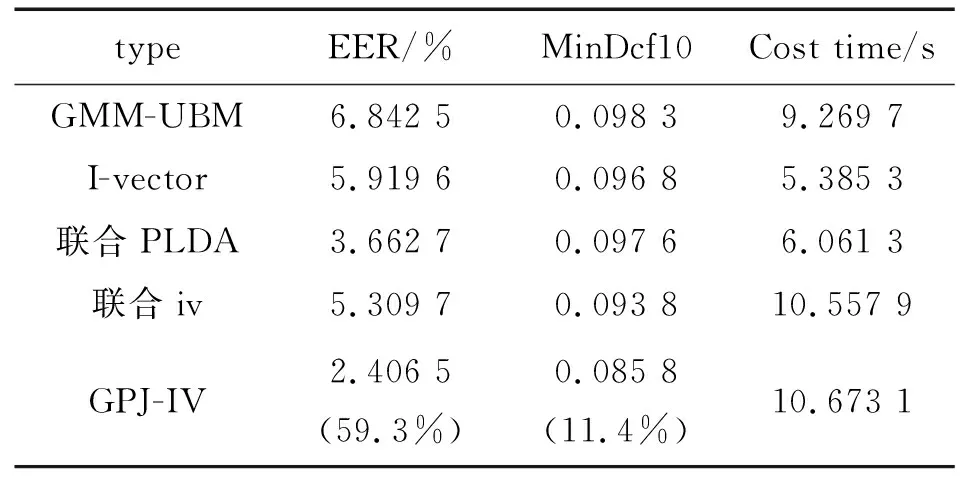
表4 MFCC特征的性能测试

表5 MFCC+LSP组合特征的性能测试

表6 MFCC+LSP+ASF组合特征的性能测试

图4、图5、图6分别为MFCC，MFCC+LSP，MFCC+LSP+ASF特征组合238个说话人语音送入238个训练好的说话人模型进行了238×238次的似然评分可视化展示，其中，横坐标为不同的测试人，数值代表测试人的标签号；纵坐标为经过训练的不同说话人模板，数值代表不同模板标签号。

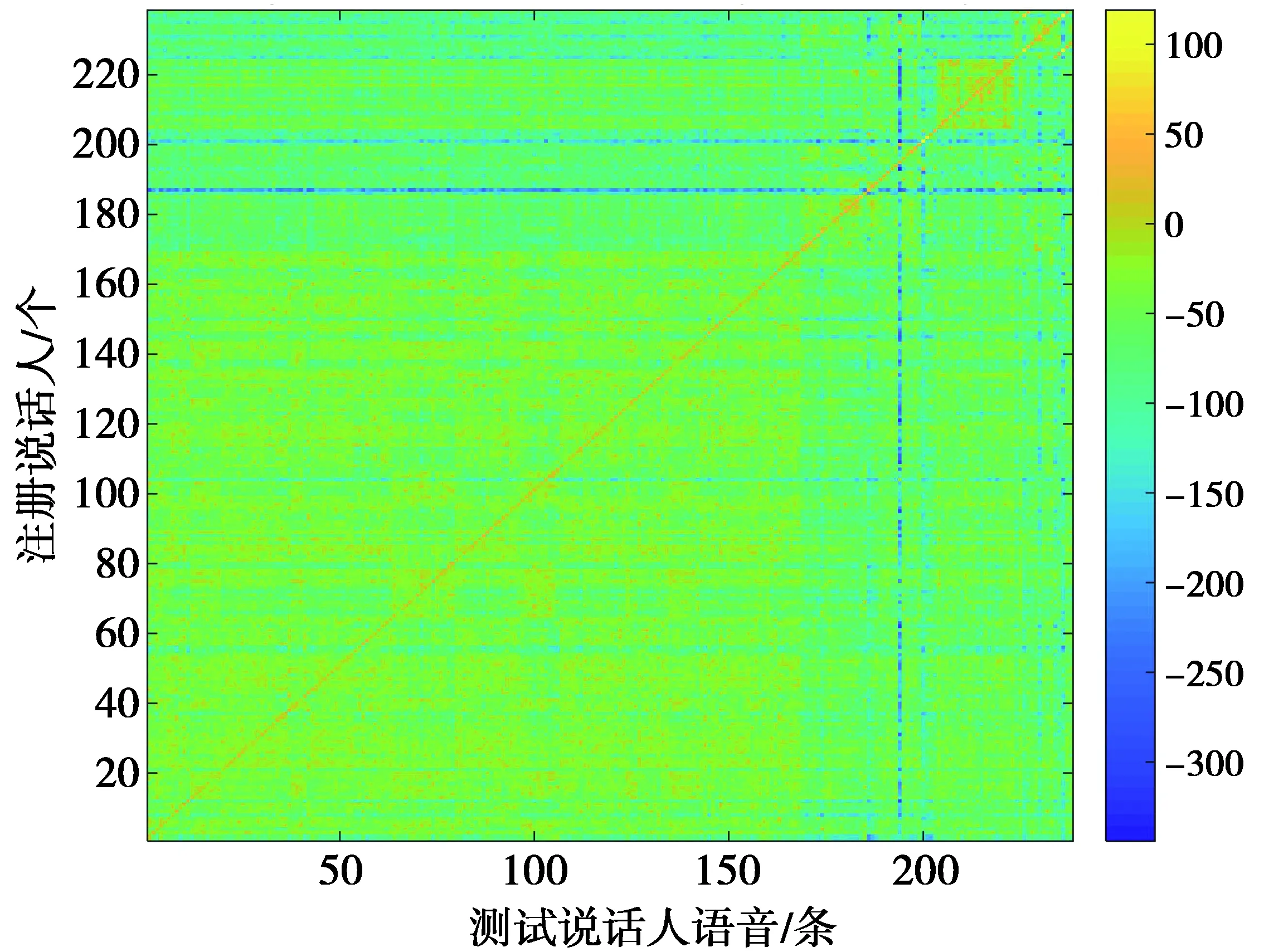
图4 MFCC特征的说话人似然评分Fig.4 Speaker likelihood score based on MFCC

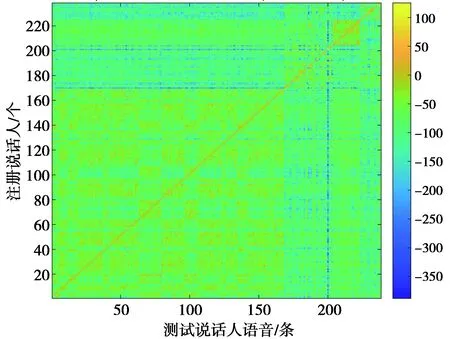
图5 MFCC+LSP特征的说话人似然评分Fig.5 Speaker likelihood score based on MFCC+LSP

图6 MFCC+LSP+ASF特征的说话人似然评分Fig.6 Speaker likelihood score based on MFCC+LSP+ASF

3.3 实验分析

由表4可知，MFCC特征送入不同说话人识别模型的测试结果中，其EER性能提高了59.3%，MinDcf10性能提高了11.4%。通过表5测试结果可知，MFCC+LSP组合特征送入不同测试结果中EER性能提高了62.7 %,MinDcf10性能也提高了17.7%。由表6可知，将特征组合MFCC+LSP+ASF送入不同说话人识别模型中其测试结果EER性能提升了54.7% ，MinDcf10性能也提高了18.5%。由表5和表4对比可知，MFCC+LSP组合特征相比于单一MFCC 特征不管对于i-vector说话人识别模型还是对于本文提出的GPJ-IV说话人识别模型在性能上都有较大的提升。表6与表4和表5实验结果分别对比可知，MFCC+LSP+ASF组合特征相对单一MFCC特征和MFCC+LSP组合特征，对于i-vector说话人识别模型和本文提出的GPJ-IV说话人识别模型在性能上也都有所提升，由此可分析得出其相对于MFCC+LSP组合特征所增加的特征组ASF确实为有效特征。分析表4—表6中的仿真Cost time(s)可知(注：此处计算的耗时仅为说话人特征送入模型进行识别的耗时)，同一特征不同模型条件下，GPJ-IV模型的耗时为i-vector模型的2倍左右，其原因为本文提出的GPJ-IV模型分别计算了基于全局差异空间T1,T2的说话人特征向量；同一模型不同特征条件下，维度越大，其计算量越耗时，与理论符合；其中识别效果最好的为基于MFCC+LSP+ASF特征的GPJ-IV模型，238人的识别耗时为12.954 6 s，人均识别耗时为55 ms，满足说话人实时识别要求。图4、图5、图6分别展示了238说话人不同特征在不同训练好的238说话人模型中的似然评分，3个图对比可知其明晰度为MFCC

4 结 论

通过实验测试结果分析可知，本文提出的基于i-vector全局参数联合的GPJ-IV模型对于i-vector说话人识别有较大的改进，并且通过分析实验结果可知，特征参数的选取和处理在整个说话人识别模型中起着不可替代的作用。并且从最终的似然评分中展示图中可见，不同语种的在同一说话人识别模型中性能也不一样，针对说话人识别问题应充分考虑说话人识别的机制，排除干扰因素(如说话人语速、情感、语种等)，突出说话人特点(如语音的整体特征、基音等)，其次对于i-vector说话人识别模型其关键是全局差异空间矩阵的求解和利用,即说话人特征的低维隐空间的基坐标。再者应充分考虑数据平衡即背景模型数据和训练测试数据的平衡，进而充分利用已有数据提高说话人识别率。