舶舶撞击荷载作用下桥梁桩基复合体系动力损伤特性分析

王祥秋，廖镇源，杨 柱

（佛山科学技术学院交通与土木建筑学院，广东佛山528000）

国内外学者针对船桥碰撞动力响应开展了大量的试验及数值模拟研究［1-5］，但针对桥墩桩基的动力响应及其损伤特性的研究相对较少，目前只有少数学者针对高承台桩与桩间土的动力响应特性开展了若干理论研究［6-7］。因此，基于船桥碰撞理论体系，深入研究桩土复合体系动力损伤特性具有重要的理论与现实意义。

本文利用ABAQUS 非线性有限元软件，对某桥梁桩基复合承载体系在船舶撞击荷载作用下的动力损伤特性进行数值模拟研究，将桥梁底部桩基以及岩土体纳入船桥碰撞复合体系，分析船舶撞击速度和撞击角度对桥梁结构以及桩基动力响应特性的影响，研究桥梁结构与桩基复合体系动力损伤特性。

1 工程背景

某桥梁结构总长200 km，为多跨连续梁结构，单跨长度12 m，桥面宽4 m，为空心混凝土结构，该桥梁结构采用直径为1 m 的灌注桩，桩长15 m，入岩深度为1 m，河道冲刷面以上的桩长为4 m，工程地质条件及结构、截面参数如图1 所示，从上至下分别为淤泥质土、粉质粘土和全风化花岗岩，各土层物理力学参数如表1 所示。

图1 桥基复合体系示意图

表1 岩土体物理力学参数

2 桥梁桩基复合体系动力损伤分析

2.1 动力有限元模型建立

2.1.1 混凝土损伤本构模型

混凝土损伤塑性本构模型（Concrete Damaged Plasticity，CDP）假定混凝土为各向同性材料，可较好地模拟混凝土在动静荷载作用下非弹性与塑性变形行为，适用于隐式和显示求解分析，可用于分析混凝土在任意荷载作用下的力学性态，在后处理阶段能较为清楚地展现混凝土结构的开裂破坏行为［8］，被广泛应用于模拟混凝土结构损伤特性。因此，本文采用混凝土损伤塑性本构模型（CDP）模拟桥面板及桩身混凝土开裂与压缩损伤特性。

如图2a 所示，在混凝土材料轴向受拉力过程中，当σt≤σt0时，材料处于线弹性阶段，弹性模量为E0；当轴向拉应力超过σt0时，逐渐出现应变软化现象；而混凝土材料在受压过程中，如图2b 所示，当σc≤σc0时，材料处于线弹性阶段，当轴向压应力超过σc0时，材料进入强化阶段，达到峰值压应力σcu时，材料刚度发生退化，材料进入应变软化阶段。处于应变软化阶段的材料弹性模量可用其卸载时的退化刚度E 表示

式中，dt、dc分别为无量纲的刚度退化系数，即受拉时的损伤因子和受压时的损伤因子，且0≤dt≤1，0≤dc≤1。

由此，混凝土材料的损伤本构关系，即损伤应力应变关系可表示为

混凝土受拉、受压损伤因子的求解方法很多，本文基于能量等效性方法计算混凝土的损伤因子［9］，具体的塑性损伤参数计算结果如表2 所示。为了考虑钢筋对桥面板以及桩身结构动力损伤的影响，本文将钢筋受力状态纳入到分析结构，并采用理想弹塑性本构模型模拟钢筋的屈服应力及塑性应变［10］。

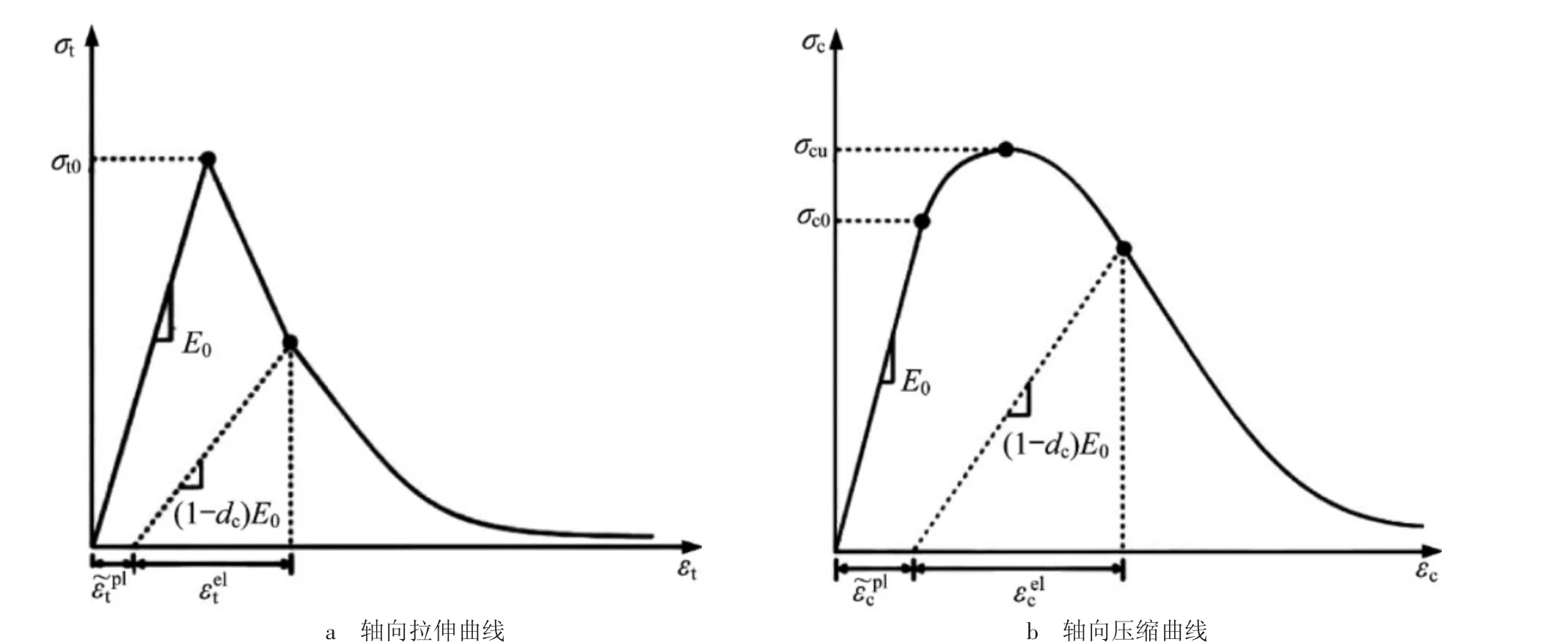
图2 混凝土应力—应变曲线

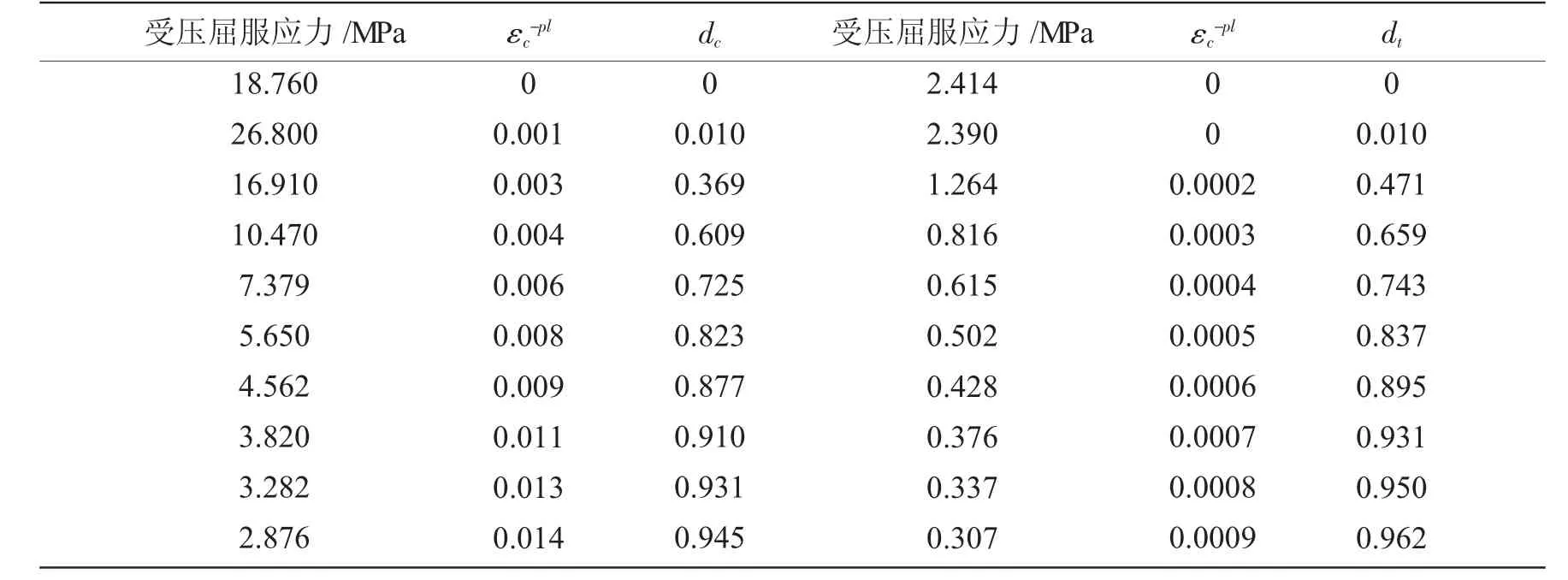
表2 混凝土材料损伤塑性参数

2.1.2 桩土动力相互作用模拟

为了有效模拟桥梁桩基与岩土体之间的动力相互作用，岩土体本构关系均采用摩尔库伦模型，在分析约束土层边界面上的法向位移时，当桩身侧向位移较少时，可近似视为线弹性问题，不考虑桩-土界面间的非线性剪切位移作用。桩身与桩间土体法向采用“硬”接触关系，而切向接触采用“罚”函数法，且切向罚函数摩擦系数取为桩侧摩擦系数，具体取值如表1。

2.2.3 几何模型与划分网格

桥梁桩基复合承载体系动力有限元分析建模时，取两跨桥梁结构为研究对象，即桥面板长28 m，宽4 m；底部桩基长15 m，其中：入岩土长度11 m ；桩周土体几何尺寸取为长×宽×深=40×15×20 m；桥面板配筋设计为箍筋Φ14@250，纵筋Φ25@150，桩基箍筋为Φ14@250，主筋为10Φ20，模型船总重为70 t。桥梁结构及岩土体采用三维8 节点六面体减缩积分单元（C3D8R）进行模拟分析，钢筋采用两节点桁架单元（T3D2）、船舶采用四结点曲面薄壳单元（S4R）进行模拟，有限元模型及网格划分如图3 所示。

2.2 分析工况

本文采用显示积分法对船桥碰撞动力损伤特性进行分析模拟。为了对比分析不同撞击角度和撞击速度对桥梁桩基复合体系动力响应特性的影响，本文假定正面撞击、偏转15°撞击和偏转30°撞击3 种碰撞工况，如图4 所示，每种碰撞工况下，船舶撞击速度分别为0.5、1、1.5、2、2.5 和3 m/s。以此分析不同碰撞工况下桥梁桩基复合体系动力损伤特性。

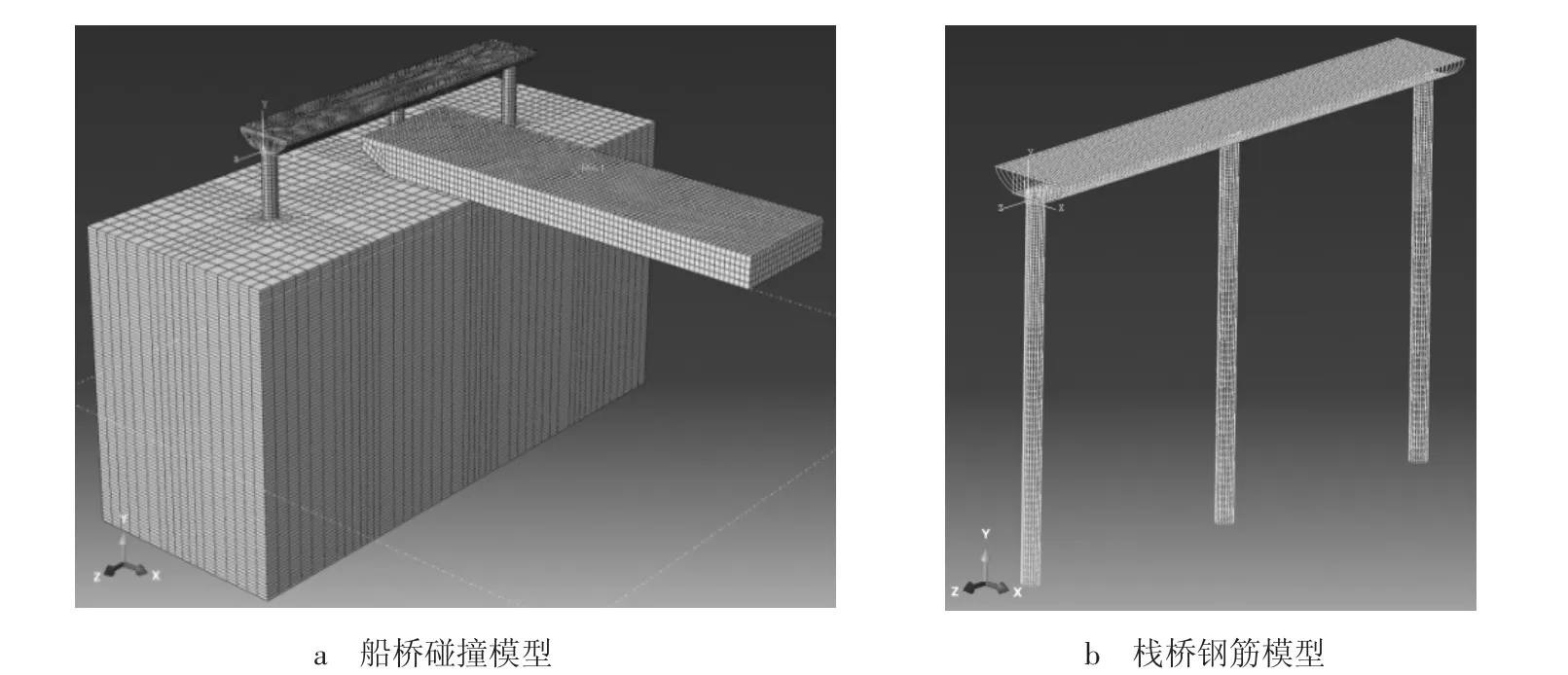
图3 网格划分示意图

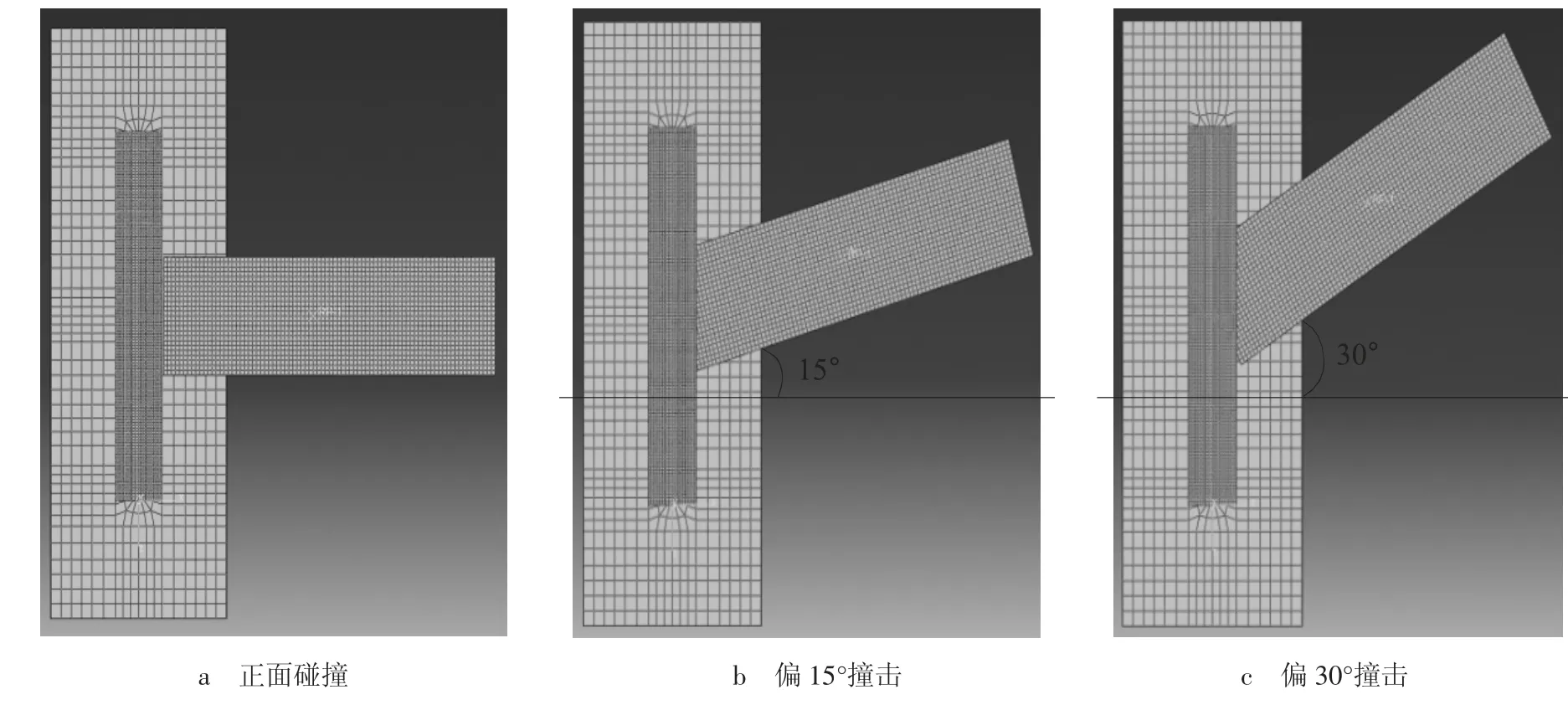
图4 撞击角度示意图

3 结果分析

3.1 撞击力时程分析

由桥梁桩基复合承载体系动力有限元分析结果，可得不同撞击工况下船桥碰撞动力响应时程曲线如图5 所示。

由图5 可知，不同撞击工况下，船桥之间的撞击力时程曲线呈现出相似的变化规律。即在船桥撞击瞬时产生的撞击力水平较低，随着时间不断增长，撞击力不断增大，并在撞击发生之后0.018～0.02 s 达到峰值，之后逐步衰减为某一定值。撞击速度与撞击角度对撞击力峰值均有显著影响，当船舶重量和撞击角度不变时，船桥之间的撞击力随撞击速度增大呈线性增长。撞击角度越大，撞击力峰值显著降低。不同撞击工况下的撞击力峰值如表3 所示。

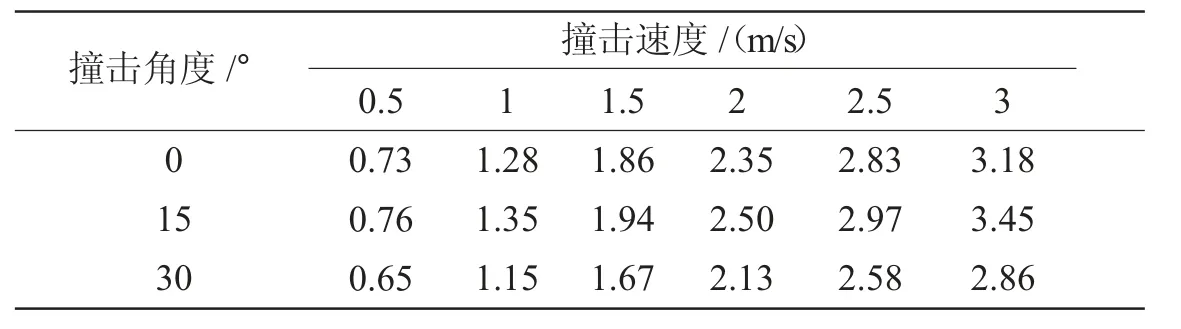
表3 撞击力峰值MN

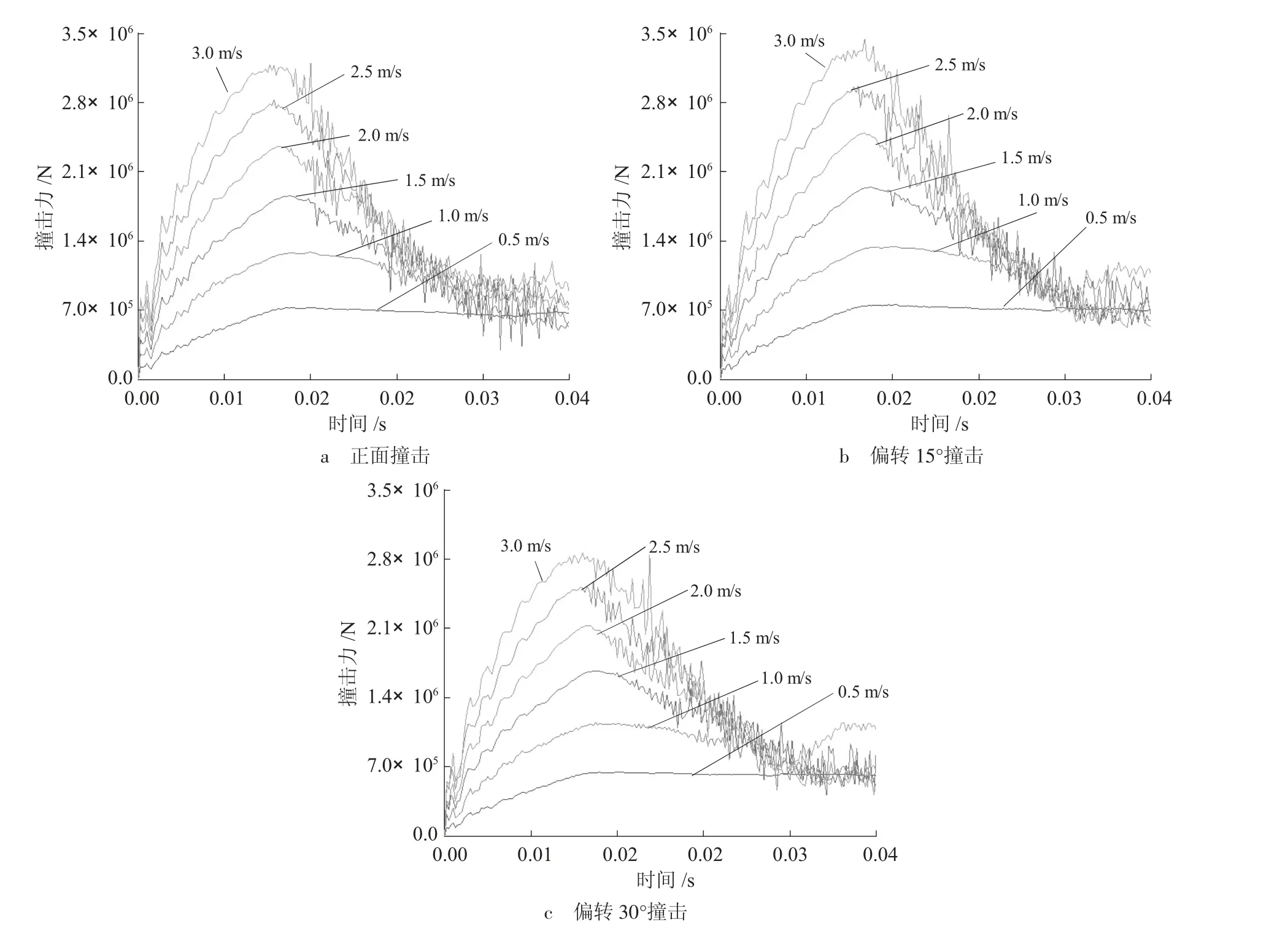
图5 不同工况下撞击力时程曲线

3.2 桩身位移与弯曲内力分析

由计算结果可得正面撞击工况在不同撞击速度下桩身最大位移变化曲线如图6 所示，桩身最大弯矩值变化曲线如图7 所示。由图6～7 可知，在船舶水平撞击荷载作用下，桩身最大位移值和最大弯矩值并未发生在撞击点，而是在撞击点以下3.0 m 左右，这可能与桩顶受到桥面约束有关。桩身位移与弯矩值均随船舶撞击速度的增大而增大。

图6 桩身位移分布曲线

图7 桩身最大弯矩分布曲线

3.3 桥桩复合体系损伤特性分析

为了分析研究桥桩复合承载体系在撞击荷载作用下的损伤特性，利用动力损伤有限元分析结果，可得船舶撞击过程中不同时刻桥面板与桩基的塑性损伤参量变化规律。为方便分析，以撞击速度为3 m/s 的正面撞击为例，不同时刻桥面板与桩基的塑性损伤云图如图8～9 所示。

如图8 所示，当船桥碰撞瞬间（即碰撞发生之后0.004 s 时），桩基与桥面板连接区域发生拉伸破坏，该区域内单元拉伸损伤参量（DAMAGET）达到0.996 以上，即桩基与桥面板连接区域处于拉伸破坏极限状态。之后随着时间的推移，桥面板以桩身拉伸损伤区域不断扩展。直至碰撞发生后0.04 s 时，拉伸损伤区域达到最大值。由此可见，船桥碰撞引发的拉伸损伤主要集中在碰撞区域附近桩身及桥面板内，桩身内的拉伸损伤随着入土深度的增加，拉伸损伤参量逐步衰减为零。

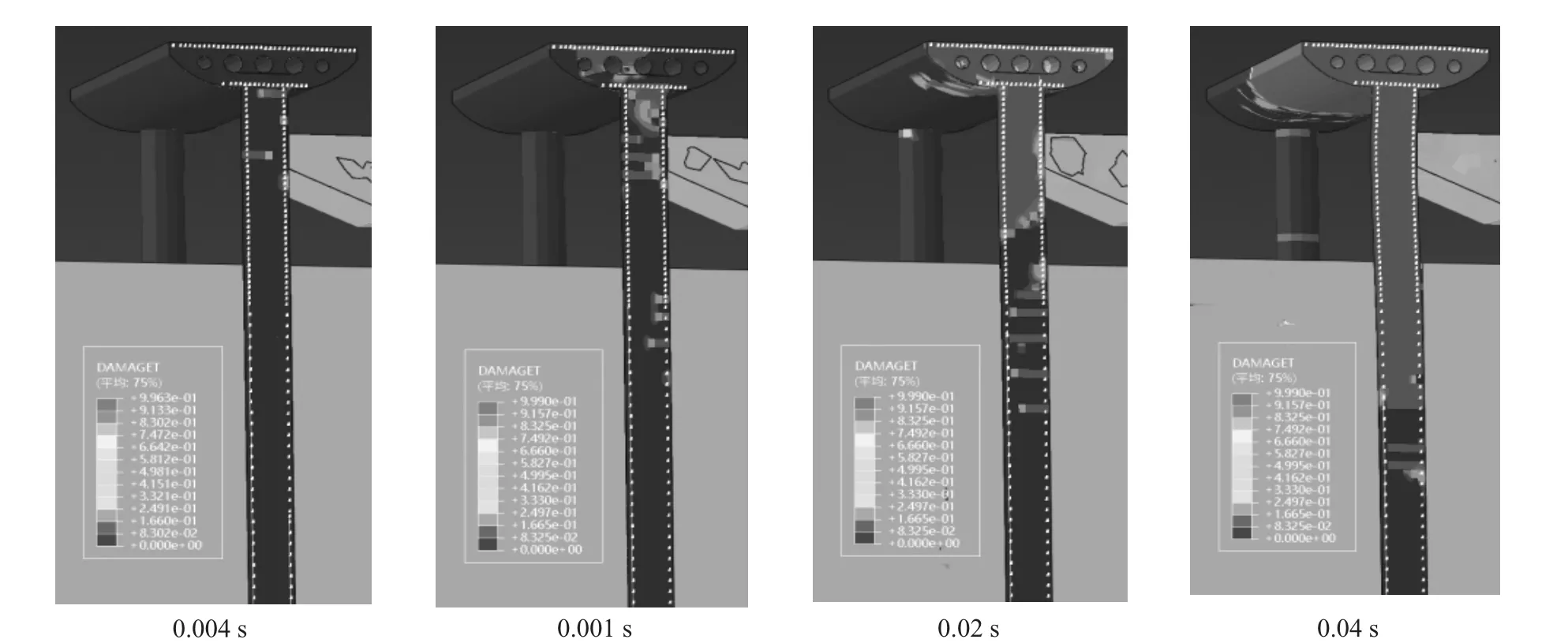
图8 栈桥拉伸损伤过程图

如图9 所示，船桥碰撞动荷载作用下桥梁桩基复合体系的压缩损伤与拉伸损伤表现出相似的发展过程。船舶撞击瞬时，首先在撞击接触表面出现局部混凝土压缩损伤，之后随着时间的推移，压缩损伤范围逐步向桥面板以及桩底方向扩展。并在碰撞发生之后0.04 s，压缩损伤区域达到最大值。由图8 和9 可知，船舶碰撞荷载作用下，桥梁桩基复合体系的动力损伤以拉伸损伤为主，压缩损伤区域面积相对较少，压缩损伤程度相对较轻（即压缩损伤参量值相对偏小）。

图9 栈桥压缩损伤过程图

4 结论

本文利用ABAQUS 动力有限元分析平台对船桥撞击动力荷载作用下桥梁结构与桩基复合承载体系的动力损伤特性进行分析，获得如下主要研究结论。

1）在船舶水平撞击荷载作用下，船桥撞击力随撞击速度增大呈线性增长。撞击角度对撞击力显著影响，撞击角度越大，撞击力峰值显著降低。桩身位移与弯矩值均随船舶撞击速度的增大而增大，桩身最大位移和最大弯矩值并非发生在撞击点处，而是在撞击点以下某一位置，这与桩顶受到桥面结构约束有关。2）船桥碰撞荷载作用下桥梁桩基复合体系的动力损伤以拉伸损伤为主，压缩损伤区域相对较少，压缩损伤程度也相对较轻。船桥碰撞引发的拉伸与压缩损伤主要集中在碰撞区域附近桩身及桥面板内，桩身内部损伤随着入土深度的增加逐步衰减为零。 3）桥梁桩基复合体系设计中，可适当提高桥梁桩基配筋率以及强化桩基与桥梁上部结构过渡段节点的整体刚度，以提高桥梁桩基复合体系抗水平撞击能力。