基于ZPD 理论的“常微分方程”变式教学
2021-03-12胡爱莲
胡爱莲
(喀什大学数学与统计学院,新疆喀什 844000)
0 引言
在大学本科数学“常微分方程”课程的教学过程中,经常遇到这样的情况:有的学生在解微分方程变式问题时,苦苦思索却不得其解,但经别人一指点,即刻恍然大悟。这说明学生头脑中已经掌握了解决这个问题所必需的基本概念、基本理论和基本方法等知识,只是不知道如何运用这些概念、理论和方法去解决眼前的问题。于是便出现了这样一个问题:怎样掌握数学知识才有助于提高学生解决数学问题的能力?或者说,怎样才能促进学生良好的数学思维与数学解题思维的有效建构?
1 ZPD 理论
苏联心理学家维果斯基提出的ZPD(The Zone of Proximal Development,最近发展区)理论认为,学生的发展有两种水平:一种是学生的现有水平,指独立活动时所能达到的解决问题的水平;另一种是学生可能的发展水平,也就是通过教师的教学所获得的潜在水平。这两种水平之间的差异就是ZPD(最近发展区),如图1 所示[1].ZPD 理论科学地诠释了在复杂的学习过程中教学的性质和形式,即:教学作为发挥潜在能力的支撑平台,赋予学习者能力,为其解决问题和建构意义提供概念框架。在教学过程中,教师应首先对学习者的现有水平进行评估,据此设计超出其现有能力但又能发挥其潜在能力的教学内容和学习任务,帮助学习者超越当前发展区,进入更高水平的最近发展区。[2]因此,我们在进行大学本科数学专业课程教学时,仅仅把课本知识讲清楚是不够的,还应针对学生的最近发展区,针对课程知识结构一环套一环的逻辑性,在变式教学的设计上注意变式间的逻辑联系,利用类比推理、化归转化等思想,预设“一题多变”“一题多解”的发散型变式和“一法多用”的聚合型变式,让学生在现有的课程知识水平基础上,通过教师教学过程中设计的一个个变式,逐步提高学生的ZPD,激发学生的学习兴趣,挖掘学生的学习潜力,提高学生解决较高难度数学问题的能力,以更好地适应数学课程的学习。那么,在大学本科数学专业课程教学中,如何通过必要的教学方法和手段把逻辑抽象、结构严谨的数学知识转化为易于调动其学习积极性、激发其潜能的能力,超越其最近发展区而达到下一发展阶段的水平呢?这是值得广大高校数学专业教师去实践探究的问题。

图1 学生两种发展水平及其差异间关系
2 基于ZPD 理论的“常微分方程”变式教学的具体实践
2.1 一题多变增强学生解决问题的变通性
在维果茨基看来,仅仅依据学生的实际发展水平进行教育是保守、落后的,有效的教学应走在发展的前面去引导发展。因此,教育者不仅应该了解学生的实际发展水平,更重要的是要了解学生的潜在发展水平,寻找其最近发展区,把握“教学最佳期”以引导学生向着潜在的、最高的水平发展[3]。课堂上,教师从原问题出发,或横向类比,或纵向深入,逐步引导学生完成预定的变式.对原问题、变式的设置要注意两点[1]:(1)原问题的选择既要简单,符合学生现有的知识、能力、情感水平,能使学生通过问题认同自己的能力,有信心顺利踏上发展的第一步;同时,原问题又要具有拓展性,可以是同一知识水平上的类比延伸,也可以是能深入挖掘的基础题型.(2)各个变式的选择要层层递进、逐步深入,这样才能让学生在现有发展水平的基础上,不断向着最近发展区努力,以求顺利地跨越当时的最近发展区,到达下一个最近发展区.
案例1从一阶齐次方程
[4]的解法入手,纵向衍生出4个变式方程的解法。
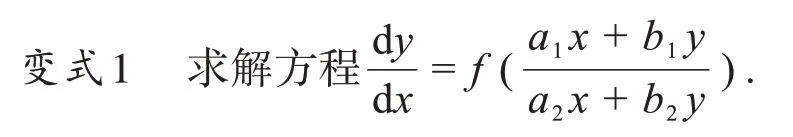
解析:此方程在原方程的基础上做了扩展,a1=b2=0,b1=a2=1 时即为原问题。此时,右端函数中分式的分子、分母同除以x,则方程的右端就变成了变量的函数.

解析:此时就是变式1,变式2的设置起到了承上启下的作用.


解析:此方程的右端函数为变量ax+by+c的函数,类似于原问题引入变量变换u=ax+by+c,可将方程化为变量可分离方程求解.
解析:此方程的右端函数中f为变量xy的函数,类似于原问题引入变量变换u=xy,可将方程化为变量可分离方程求解.

解析:此方程的右端函数中f为变量的函数,类似于原问题引入变量变换u=,可将方程化为变量可分离方程求解.
变式 4 求解方程f(xy)y+g(xy)xy′=0 (f(t)≠g(t)).
解析:此方程的左端函数中f,g为变量xy的函数,类似于原问题引入变量变换u=xy,可将方程化为变量可分离方程求解.
案例1 和案例2 将原问题1 从纵向、横向两个方面各产生了4个变式,都符合变式设置的两个要求,由原问题到变式,难度在逐步加深,对学生的要求在逐渐提高,随着变式教学的推进,学生从一个ZPD 发展到一个更高的ZPD,层层递进,不断引导和激励学生,使其两种发展水平呈螺旋式上升,最近发展区呈波浪状前进.[5]
2.2 一题多解提升学生解决问题的能力
“常微分方程”各个知识板块之间不是割裂的,相互之间存在着内在联系.我们在学习一个新知识时,要注意建构新知识与已有知识间的联系,把各个知识点联系起来,引导学生逐步建立起属于自己的知识结构体系,这样学生就不再惧怕解决数学问题.而这种联系,主要是靠“一题多解”来实现的。在已有知识储备的前提下,通过用不同的方法解决同一问题,在这个过程中不断寻找和建立新旧知识之间的内在联系,既开拓了学生的数学思维、巩固重构学生的知识结构体系,又可超越学生已有的最近发展区,达到下一发展阶段的水平,进而提升学生解决数学问题的能力.
案例3通过问题2 的三种不同解法,演示如何通过一题多解提高学生的发展水平.


以上三种方法通过将方程进行适当的改写,使其成为不同类型的一阶显示微分方程,再用相应方程的解法进行求解,导致了同一方程的不同解法。教师在教学中应引导学生主动思考,体会三种方法的本质,提高学生领悟数学本质的能力,同时也发展了学生的ZPD,利于其数学思维能力的提高.
2.3 一法多用激活学生解决问题的聚合性
基于ZPD 理论的常微分方程变式教学,仅仅停留在“一题多解”的发散型变式教学,可能会出现学生的数学思维得到了发散,但却忽视了思维的聚合性,也就是要及时归纳总结各类方程的求解方法,促进学生数学思想方法系统性的形成.而常微分方程的“一法多用”的聚合型变式恰好能弥补这个缺憾.
“一法多用”型变式是将所要求解的结构形式不同的常微分方程进行局部调整,变成解法相同或类似的问题,这样可以强化学生对某一种解法的掌握,同时,也以此为依据来解决其他问题.
案例4通过不同的一阶微分方程改写成微分形式,求得其积分因子,进而将原方程化为全微分方程进行求解.
原问题3 求解(y2+x2+x)dx+xydy=0.
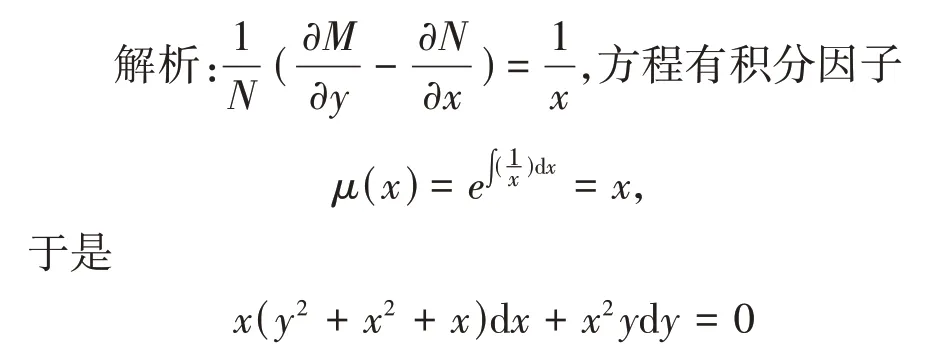

案例3的设置,可以让学生体会到不同的一阶显式微分方程间的潜在关联,从而归纳总结出解这一类题的通用解法——积分因子法,提升了学生的数学思维和解决问题的能力水平.
案例5常数变易法在不同微分方程(或方程组)的求解中的应用.
解析:此方程就是原问题2,其解法一就是常数变易法.

变式4 求解方程y˙+3y″+3y′ +y=[6].
解析:方程对应的齐次方程的特征方程为λ3+3λ2+3λ+1=0,解得λ1,2,3=-1,故对应的齐次方程的通解为

从案例3、4 可以看出,教师要引导学生对同一方法在不同问题中应用的重视,帮助学生寻求某一类题的常规通用解法,教学中要弱化针对性技巧,重视对一类问题通用解法的训练.这样不仅能达到触类旁通、举一反三的效果,还能拓宽学生的视野,启发学生思维并提升学生数学思维能力,尽可能激发学生潜能,将学生的ZDP 提升到一个新的阶段,使学生不断在学习的过程中提高解决数学问题的能力.
3 总结
数学知识之间具有严密的逻辑性和知识的层层递进,学生头脑中形成的数学知识不是教师通过课堂训练所形成的知识体系,而是学生通过主动思维在头脑中对自己的理解进行建构而形成的。许多新的知识背后都有它所对应的原有基础知识,教师在教学中要根据学生已有知识水平,在旧知和新知之间构建联系的桥梁,激发学生对已学知识的再认识,激起学习对新知识的欲望,经过对新知识的迁移、发展形成下一个发展区。这就是创造最近发展区并使最近发展区转化为现有发展水平的过程。遵循ZPD 理论的常微分方程变式教学能让学生的最近发展区得到很好的发展,尤其是在课堂中有针对性的适度的运用变式教学,充分发挥学生的内在潜能,不仅能提升学生的思维水平,还能提高学生解决问题的能力,是一种切实可行的教学方法.
