海峡两岸教材中分数内容的对比与教学建议
2021-03-12李玲玲
李玲玲
(福建省厦门市音乐学校)
三千多年前,古埃及为了在不能分得整数的情况下表示数,用特殊符号表示分子为1 的数。分数是度量和数学本身的需要——除法计算的需要而产生的,分数内容历来就是数学教学中的难点。德国谚语“掉到分数里去了”就用来形容一个人陷入困境。在实际的教学过程中,我发现“掉到分数里”的学生也为数不少。比如,我在教学教研过程中记录下这样三个教学事例。
事例1:有一位五年级的学生,在学完“分数的意义”后,作业中有一道题目要求写出分数各部分名称时,她抬头询问:“中间那条线叫什么?”
事例2:“把3 米长的绳子平均分成7 段,每段占这条绳子的每段长( )米。”在这个空格中,不少学生直接填上了循环小数。
事例3:五年级下学期“假分数”一课,在认识了假分数后,有学生举手表示有问题:“老师,这个假分数也太‘假’了!”(其他学生笑了起来)教师让学生说想法。“我们知道是表示把一个物体平均分成5份,取其中的2 份,那就是表示把一个物体平均分成5份,取其中的6 份,明明只有5 份,怎么能取其中的6份呢?”这位学生的质疑得到很多其他学生的支持。
这些问题在教学中经常出现,长期以来没有比较好的解决策略。近期,我阅读了我国台湾地区康轩版小学数学教材,并与我们当前使用的人教版教材中的分数内容编排进行了对比分析研究,得到了一些教学建议。
一、对比教材编排,理解学习困难
通过阅读这两种版本的教材,我认为,在“分数”这部分内容的编排中,两种版本教材的呈现方式各有特点,同时也存在着较大的区别,我对两种版本教材关于分数内容的编排进行了梳理,如表1所示。

表1 海峡两岸教材中分数内容的编排
从表1 中可以看出,两个版本教材关于分数编排有很大的区别,主要体现在两个方面:一是例题与习题数量。在题目总数相差不大的情况下,人教版教材的例题数量远远少于习题数量,康轩版教材的例题比习题数量略多。二是各年级的学习内容分布情况。两种版本都是在三年级上册开始接触分数,到六年级下册结束小学部分的分数学习。但不同的是,人教版教材从三年级上册“分数的初步认识”一单元,到再次正式学习分数内容要到五年级下册。康轩版教材则从三年级上册开始,每一册均有编排相关的分数学习内容,体现了小步子螺旋上升的特点。
因为学生在生活经验中比较少接触到分数,对于他们来说属于比较抽象的学习内容。人教版小学数学教材从三年级上学期到五年级下学期,中间隔了四个学期没有正式学习与分数的相关内容,学生普遍对分数比较生疏。因此,上文事例1 中出现的学生产生对分数线不认识的现象,属于正常情况。教材编排是个系统工程,对于一线教师来说,教材是最重要的教学载体,大幅度改造教材不现实,但基于学生的学习困难,笔者认为,可以在原教材的基础上进行适当的改组,帮助学生突破学习难点。
二、拓展测量意义,丰富概念理解
在小学阶段,分数有多种定义,如部分与整体关系、商定义、运算定义、测量定义、比定义。这五种定义可以归为两类,也就是常说的“量”和“率”含义。分数的“率”含义表示部分与整体的关系,是一个比率;分数的“量”含义表示一个具体的量,和整数一样是数量的抽象。在人教版小学数学教材的编排中,“率”含义受到重视,而“量”含义显然被忽视的。人教版与康轩版教材对“分数的初步认识”的编排,都是以分饼为情境(如例题1)。
【例题1】把一个酥饼平分成2 份,其中的1 份是二分之一个酥饼。二分之一记成

人教版教材“每份是它的二分之一”表示的是部分与整体的关系,是“率”含义,相应的练习都均已“率”含义出现;而康轩版“其中的1 份是二分之一个酥饼”表示的是具体的数量,并且在相应配套的课后习题中(如例题2),不断强化学生对“分数是一个具体的量”的认识。
【例题2】涂色的部分是多少?填填看。
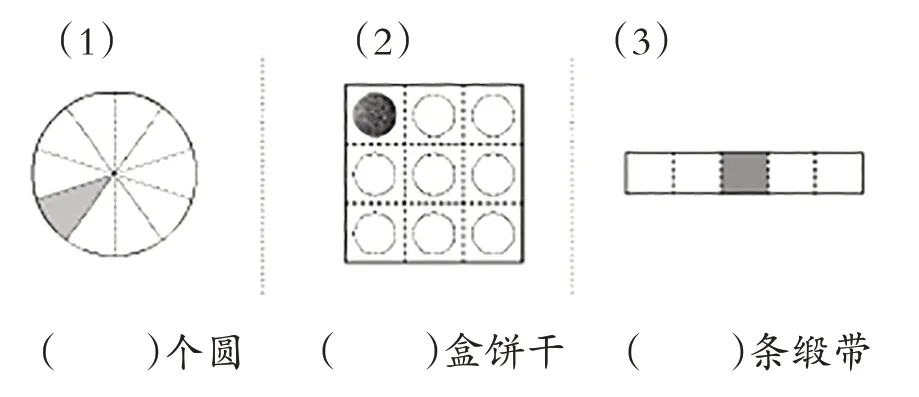
著名特级教师俞正强曾在“认识分数”一课中,只教学“量”的含义,他认为,“解决之道是让学生先深刻地经历关于量的分数的认识,记熟之后,再经历关于分率的分数的认识,在此基础上比较两个认识的差别,以此解决量与分率的混淆问题”。而他建议“量”的含义学习完,一年后再学习“比率”含义,这样,学生可以加深对“量”含义的认识。可以说,俞老师的设计跟康轩版教材的编排有相通之处,给我们提供了改造教材的启发。
无独有偶,著名特级华应龙在“分数:先分后数”一文介绍了关于分数的意义的教学片断。华老师首先让学生回顾要量教室、粉笔、米粒的长分别用什么做单位,然后指出:“单位不同,尺子就不一样。创造一把尺子,其实就是创造了一个新的单位。所以大头儿子在家中没有找到尺子,用领带创造了一个单位。请回头看,刚才我们说沙发是个领带长里有7个”从这里我们可以看出,华老师也是从“量”的含义引出分数的意义。把分数看成是“分数单位的累加”不仅延续了自然数的认识,又为进一步理解分数的性质以及分数的加减运算打下了坚实的数学基础。前文提到的事例2 学生不认为分数可用来表示具体的量,事例3 中的学生认为“假分数很‘假’”的问题,与教师在教学单方面强调“率”的含义是有相关性的。如何处理“量”与“比率”含义的理解呢?两位名师的做法给了我们很大的启示。
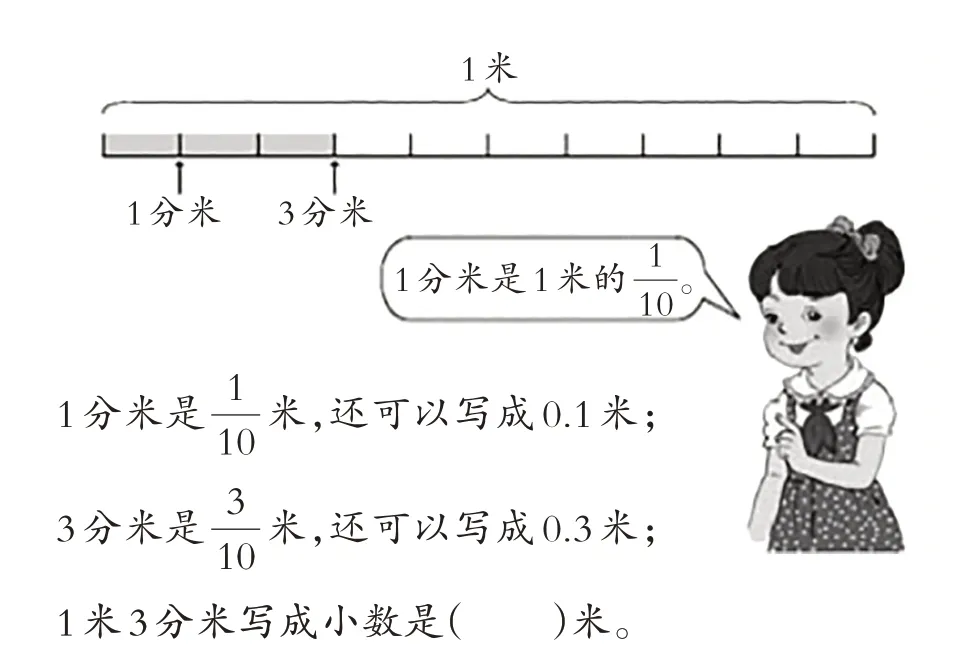
人教版小学数学教材三年级下册“认识小数”里的表述“1分米是米,还可以写成0.1米。”(如例题3)这里借助分数引出小数。但借助的分数是“量”含义的表示,而在此之前,教材没有出现过正式的用“量”表示的分数,造成的结果是学生能理解“1 分米是0.1米”,而不能理解“1分米是米”,从分数引出小数的编排意图成了一种摆设。因此,在学习“分数的初步认识”后补充分数“量”含义的相关教学,既是丰富对分数概念的理解,也是后续学习的基础。
【例题3】把1米平均分成10份,每份是1分米。
作为一名普通的一线教师,完全推翻教材另组教材不现实也没必要,但可以适当进行拓展,比如在人教版小学数学教材“分数的初步认识”一课教学中,引出“每份是它的二分之一”后,可以再加“也可以说是‘二分之一块月饼’”,在相应的巩固练习中,也借鉴康轩版做法增加一些用“量”含义写分数的练习。
本单元的练习题(三年级下册教材第95 页)有一道出现一家三口分月饼的情境,我认为可以直接改变题目,在分数后面加上“块”,引导学生直接表述为“爸爸吃了块,妈妈吃了块,我吃了块,还剩下块。”这样的表述,既跟生活语言比较接近,又让学生加强对分数“量”含义的理解,从而丰富对分数的全面认识。
三、重视数线表征,培养几何直观
【例题4】分数数线。

(1)上图是1公升的量杯。用分数说说看,由下往上数,第1刻度表示多少公升?第2个刻度呢?……
(2)这是一条整数数线。

(3)把每一段都分成3 等分,每一个刻度各表示什么数?用分数记记看

人教版小学数学教材从一年级开始,在认识整数时就出现了让学生在数线写数,在三年级下册“小数的初步认识”单元练习题中,也出现了在数线上填小数的题目,但在分数的初步认识单元中却没有出现。原因主要是因为在此单元中分数是主要以“率”的含义出现的,不便于在数线上呈现。因此,在分数的认识时,除了拓展分数的“量”含义,还可以借助数线进行表征。我校一位教师在教学“分数的初步认识”一课时就引入了数线,以下是教学片断。
【片断一】情境引入
师:想一想,1 个月饼用什么数表示?2 个月饼用什么数表示?3 个月饼呢?没有月饼用什么数表示?(学生逐一回答1、2、3、0)
师:我现在要将这些数请到这条线上来。0应该安顿在这条线的什么地方?
生:放在1的前面。
师:孩子们,像0、1、2、3……这些数都是同学们学过的数。
师:我这儿有半个月饼,我该把它放在哪儿呢?
生:放在0和1之间。
(师放于数线上,如下图)
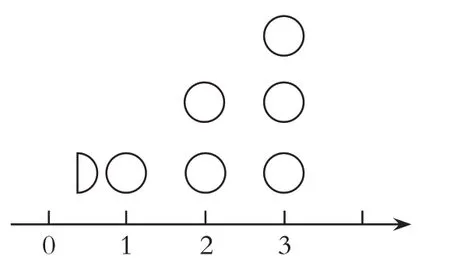
师:想一想,“一半”可以用一个什么样的数来表示呢?
生:二分之一。
师:这就是我们今天要学习的新数,叫做分数,让我们一起来认识分数。
【片断二】拓展提升


师:试着说说你的理由。
生:比较图上的阴影部分的大小可以发现。
师:试着在线上找到他们的位置。谁上来写一写。
生:我是这样写的。
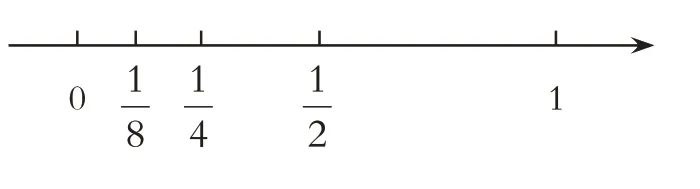
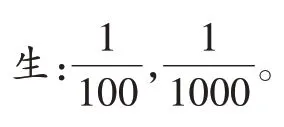
师:你为什么尽量把分母说大?
生:因为分母越大,这个分数就越小。
师:是的,分数比较大小,分子相同,分母越大,分数就越小。
生:分子相同,分母越大,分数就越小,在这条线上就越靠近0。
从整数到分数是数的概念的一次扩展,这个学习过程对于学生来说并不轻松。从学生的思维特点来看,他们对分数概念的理解,几何直观发挥了重要的作用。在以上两个片断中,这位教师将整数和分数分布在数线上,并引导学生在数线上进行分数大小比较,不仅丰富了对分数概念的理解,也在数形结合的过程中培养了几何直观能力。
