云制造环境下指标协同效应的双边匹配方法研究

2021-03-12耿秀丽赵灵玮宗天华

软件导刊 2021年2期

程磊，耿秀丽，赵灵玮，宗天华

（上海理工大学管理学院，上海 200093）

0 引言

随着全球经济高速发展，我国制造业处于大批量制造转变为服务型制造时期，满足用户个性化需求以及柔性制造的优势开始显露。由于市场快速转变，许多企业在面临用户多样化、个性化需求时，出现自身制造能力不足，或是因为市场需求较小，造成企业资源闲置和浪费等问题。在此供需不匹配的市场下，人们开始重视云服务制造。云制造将动态、可虚拟化的资源或服务通过网络提供给需求方，将分散或闲置的制造资源整合起来，通过平台对资源或服务的匹配进行优化，使其分配更合理。在互联网快速发展的环境下，许多制造企业通过云制造平台实现资源整合，根据需求变化及时调整生产规模，实行产品全生命周期的管理和优化的新型制造系统，推动生产方式向定制化、柔性化转变。在云制造平台中，为供需双方提供最优双边匹配十分重要。双边匹配理论主要探讨双方互相选择过程中如何充分考虑双方主体偏好，使双方满意度达到最大化，以达到提升市场资源利用率目的。基于云制造环境下的供需双方资源匹配是一个典型的双边匹配问题，也是目前的研究热点。

双边匹配最初由Gale 等［1］于1962 年提出，最早研究的是婚姻匹配和大学生录取问题。随后双边匹配广泛应用到各领域，如云制造中资源和服务的匹配［2］、金融市场风险投资［3］以及人员和岗位的匹配问题［4］。文献［5］通过假设云平台面对多个双边市场，对双边匹配稳定机制进行研究，运用算法拓展云平台中多对多的匹配问题；文献［6-7］通过将多种类型评价指标体系进行转化，建立双边匹配优化模型；文献［8］针对信息不确定性等因素影响，采用灰色关联分析法编制算法，求解多目标双边匹配模型；文献［9-10］通过改进匹配算法，对双边匹配的稳定性进行分析。相关研究大多从匹配机制、匹配稳定性、双边匹配算法以及多种类型的评价指标等角度，对双边匹配问题进行探讨，以期望效用理论和满意度为基础，构建双边匹配模型。

许多学者在研究双边匹配问题时多假设匹配双方主体是完全理性的，但在现实中，由于问题的复杂性、不确定性以及认知局限性等因素影响，决策主体往往是有限理性的，还要考虑双方主体的心理行为对双边匹配决策产生一定的影响。文献［11］采用直觉模糊形式表示主体偏好信息，最大化双边主体满意度；文献［12］针对不确定、不完全语言环境下的双边匹配，通过将偏好信息转化为二元矩阵建立双边匹配模型；文献［13］从后悔理论出发，将决策主体与其它主体匹配结果进行对比，获取决策主体感知效用大小，建立双边匹配模型；文献［14］建立一种多阶段双边匹配模型，根据决策者的反馈以及收益建立优化匹配模型；文献［15］利用直觉模糊数建立满意度矩阵，构建双边匹配满意度指标体系，构建多目标决策模型得到最终匹配结果。上述文献在介绍双边匹配时，考虑决策主体是非完全理性情况，或者假设多个指标之间是独立的，但较少研究多个指标之间也会产生协同效应而对决策主体偏好产生影响。

Choquet 积分可以对指标评价值进行集结，充分考虑指标间的相互关系，使信息集结结果更加准确，是分析指标关联关系的有效工具。因此，本文提出一种考虑指标协同效应的云制造资源双边匹配决策方法，利用Choquet 积分集结指标关联性特征，综合考虑评价指标之间的协同效应对主体匹配产生的影响，通过构建合理的双边匹配方法，提高企业资源利用率和灵活应变能力，在云制造资源大环境下使企业能够快速适应市场环境改变。

1 基础知识

1.1 双边匹配

在云制造资源双边匹配过程中，假设存在X=｛X1，X2，…Xm｝，表示云制造资源需求方集合，Y=｛Y1，Y2，…Yn｝，表示云制造资源供应方集合，其中Xi表示第i个需求方（i=1，2，…，m），Yj表示第j个供应方（j=1，2，…，n）。

定义1［16］：给定μ：X∪Y→X∪Y 上的映射，若∀Xi，∀Yj满足：

μ（Xi）∈Y；

μ（Yj）∈X∪｛Yj｝；

μ（Xi）=Yj，当且仅当μ（Yj）=Xi

则称μ为双边匹配，其中μ（Xi）=Yj表示Xi和Yj在μ中匹配，μ（Yj）=Yj表示Yj在μ中未匹配。

云制造资源需求方主体Xi利用多个具有相关关系的评价指标对供应方主体Yj进行评价。假设需求方主体Xi对供应方主体Yj进行评价的指标集为C=｛C1，C2，…，Ch｝，Cp表示第p个评价指标（p=1，2，…，h），评价值为R=｛R1ij，R2ij，…，Rpij｝，Rpij表示需求方Xi对供应方Yj的第p个指标评价值。供应方Yj对需求方Xi进行评价的指标集为D=｛D1，D2，…，Df｝，Dq表示第q个评价指标（q=1，2，…，f），评价值为S=｛S1ij，S2ij，…，Sqij｝，Sqij表示主体Yj对主体Xi针对第q个指标的评价值，其中Rpij和Sqij是决策主体以［1，10］的分值形式进行打分，分数越高代表指标满意度越高。

本文针对云制造资源匹配过程中评价指标之间具有关联关系的特点，依据双边主体给出的综合评价信息建立多目标规划模型，使双边满意度达到最大。

1.2 Choquet 积分及相关定义

法国数学家Choquet［17］提出非可加性测度研究，日本学者Sugeno［18］随后提出模糊测度概念，用来解决事物属性之间存在着关联关系的多属性决策问题。在云制造资源双边匹配问题上，许多学者假设评价指标之间是相互独立没有关联的，但在现实中指标之间往往不是独立的，彼此之间有一定联系，对最终决策主体的评价结果会产生一定影响。因此，本文采用Choquet 积分分析指标之间的关联关系，将其应用到云制造双边匹配问题中。首先给出Cho⁃quet 积分概念及计算公式。

定义2［19］：设A=｛a1，a1，…，an｝为一有限集，μ为幂集P（A）到［0，1］上的函数，ai表示第i个元素，若满足：①μ(∅)=0，μ（A）=1；②∀I,J∈P(A)，I⊆J，且有μ(I) ≤μ(J)，称μ是A上的模糊测度。

若∀I,J∈P(A)，I⋂J=∅，模糊测度μ满足：

μ(I⋃J)=μ(I) +μ(J) +λμ(I)μ(J),λ∈(-1,,∞)（1）

则称μ是A上的λ-模糊测度。当λ=0 时，表示μ为A上的可加测度，代表集合I、J之间互相独立，当λ≠0 时，表示μ具有非可加性，I、J之间存在关联关系；若λ ＜0，μ(I⋃J) ＜μ(I) +μ(J)，则μ是A上的次可加测度，表示集合I、J间相互存在信息冗余，有替代作用；若λ ＞0，μ(I⋃J) ＞μ(I) +μ(J)，则μ是A上的超可加测度，表示集合I、J存在信息互补。

在具有关联关系的多属性决策分析中，λ-模糊测度可精确表述指标间的相互关联关系。因此，对多指标存在关联情况，可通过Choquet 积分进行集结运算。其中指标集代表定义1 中的集合A，各指标子集的重要度即为集合A的模糊测度。若非空集合A=｛a1，a1，…，an｝，∀i,j,…,n,i≠j，ai⋂aj=∅,那么，则λ-模糊测度μ满足：

由式（2）可知，对∀I∈P(A),有：

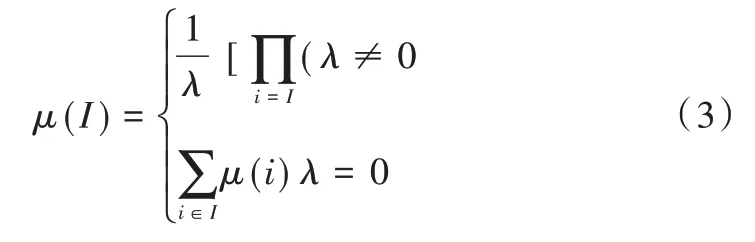
由边际条件μ（A）=1，根据式（2）和式（3），可由以下方程确定参数λ：

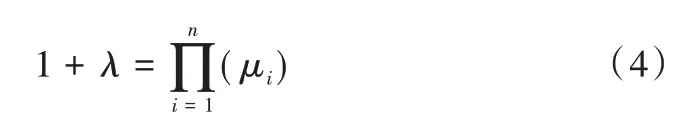
定义3［20］：若μ是A上的模糊测度，f为定义在A上的非负实值函数，则函数f关于μ的Choquet 积分集结计算公式为：

函数f关于μ的离散Choquet 积分集结计算公式为

其中，（i）是按照0 ≤f(A1) ≤… ≤f(An)进行排序之后的下标，Ni={x(i),…,x(n)},i=1,2,…,n;x(0)=0。

2 云制造双边匹配方法

2.1 考虑指标协同效应的满意度计算方法

考虑用Choquet 积分集结多个存在关联的评价指标，假设指标集C=｛C1，C2，…，Ch｝和D=｛D1，D2，…，Df｝的多个评价指标之间也存在关联关系。由于决策主体受问题的复杂性和模糊性等因素影响，所以对同一指标，不同的决策主体可能会有不同的认可度。由此可根据供需双方给出的指标评价信息集结指标权重作为评价指标的模糊测度，根据公式（4）计算出参数λ，由式（2）和式（3）得到各评价指标集的λ-模糊测度。

按照指标C1，C2，…，Ch评价值将R1ij，R2ij，…，Rpij从小到大排序，使得评价指标C'1,C'2,…C'h下的评价值R'1ij,R'2ij…,R'pij大小关系为R'1ij≤R'2ij≤… ≤R'(p-1)ij≤R'pij。根据式（6）计算出需求方主体Xi对供应方主体Yj的满意度评价值，其计算公式为［21］：

其中，R0ij=0为评价指标集C'1,C'2,…C'h的λ-模糊测度。

按照同样方法可得到供应方主体Yj对需求方主体Xi的满意度评价信息，计算公式为：

其中，S0ij=0，为评价指标集D'1,D'2,…D'f的λ-模糊测度。

考虑到各决策主体都是理性的，即决策主体对另一方满意度敏感性［22］有逐渐递减趋势，通过公式（9）计算供需双方的最终满意度：

其中，maxαij表示需求方主体对供应方主体偏好的最大值，maxβij表示供应方主体对需求方主体偏好值的最大值。

2.2 双边匹配模型构建与求解

根据上述分析，获得供需双方关于指标协同效应的满意度，构建基于最大化满意度的多目标优化模型：

公式（10）代表最大化需求方主体满意度，公式（11）代表最大化供应方主体满意度，公式（12）表示每个X方主体至多与一个主体Y匹配，公式（13）表示每个Y方主体至多与一个X方主体相匹配。其中，xij为0-1 型决策变量，当xij=1 时，代表指标Xi与Yj相匹配；当xij=0 时，代表主体Xi与Yj不匹配。

在模型（10）中，目标函数的量纲级相同，依据文献［21］提出的核心竞争理论，稀缺资源具有更大的竞争优势。因此，在双边匹配中，数量较少的一方占有优势地位，提出匹配相对竞争度概念，X方以及Y方的匹配相对竞争度为：

将其转化为单目标规划模型为：

其中ω1、ω2分别表示目标函数Z1、Z2的权重系数，且满足0≤ω1、ω2≤1。式（16）—式（19）是单目标规划，其约束和目标函数均是线性的，可采用线性规划方法求解，如优化软件包或遗传算法编程等。通过求解模型，获得X方以及Y方的双边匹配结果。

3 案例分析

云制造由于集合了多方供需企业，以最大化资源使用率与服务满意度为目标，为企业生产提供优质高效的原料，成为学者研究热点。假设一云制造服务平台上有5 家需求商（X1，X2，X3，X4，X5）发布某种制造资源的需求信息，有6 家企业（Y1，Y2，Y3，Y4，Y5，Y6）是关于该种制造资源的供应方。从众多文献研究及决策者、行业专家学者意见中提取10 个评估指标，对需求方与供应方进行匹配［23］。从需求方对6 家制造资源供应商从制造技术水平C1、产品价格C2、企业信誉C3、交货期C4、售后服务C5等方面进行多指标综合评价，从供应方根据需求方的制造工艺复杂程度D1、交货期D2、企业信誉D3、生产成本D4等指标进行综合评价。

考虑到决策主体采用多个指标进行偏好评价时指标之间往往会存在关联情形，并不是完全独立的，如企业信誉（C3）和交货期（C4）是具有相关关系的评价指标。根据前述给出的方法进行分析。需求方Xi对供应方Yj针对指标Cp的评价信息如表1 所示，供应方Yj对需求方Xi针对指标Dq的评价信息如表2 所示，以1-10 分值代表对各个指标的偏好程度。

Table 1 Matching index evaluation information of supplier Yj by demand side Xi表1 需求方Xi 对供应方Yj 的匹配指标评价信息

Table 2 Matching index evaluation information of supplier Yj to demander Xi表2 供应方Yj 对需求方Xi 的匹配指标评价信息

双边决策主体对不同指标具有不同认可度，由双方给出的匹配指标评价信息可计算不同决策主体下的指标权重，如需求方主体X1在评价指标（C1、C2、C3、C4、C5、）下的评价值向量为（40，34，37，36，39），计算得到需求方主体X1对所有评价指标权重为（0.215，0.183，0.199，0.194，0.210），同理可得其他需求方对应评价指标权重如表3、表4 所示。

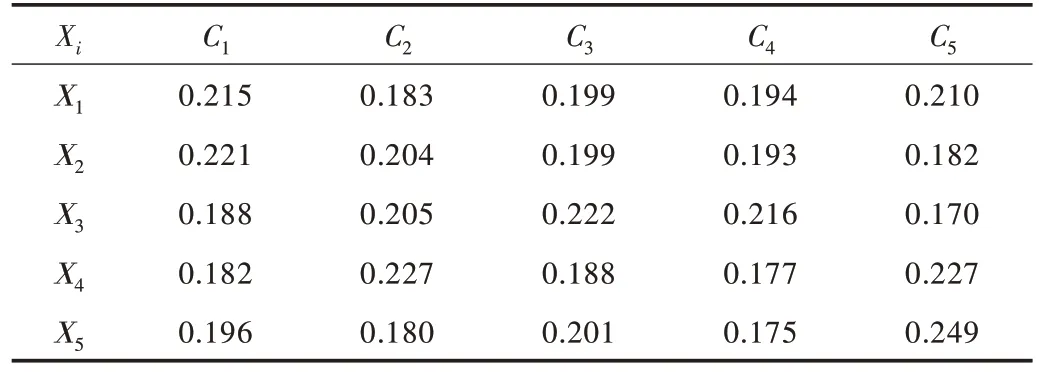
Table 3 Index Evaluation Weight of Demand Side Subject Xi表3 需求方主体Xi 的指标评价权重

根据需求方和供应方评价指标权重，由式（4）计算得到所有需求方主体的λ-模糊测度的参数：λ1=-0.002 5，λ2=0.002 5，λ3=-0.002 5，λ4=-0.002 5，λ5=-0.002 5，以及所有供应方主体的λ-模糊测度的参数：λ′1=0.002 7，λ′2=-0.002 7，λ′3=0.002 7，λ′4=-0.002 7，λ′5=0.002 7，λ′6=-0.002 7。由公式（3）计算各指标集的λ-模糊测度，对｛C5｝，｛C4、C5｝，｛C3、C4、C5｝，｛C2、C3、C4、C5｝，｛C1、C2、C3、C4、C5｝分别计算出相应的模糊测度向量，如需求方主体X1指标集C=｛C4、C5｝的模糊测度计算步骤为：(xi)) -1]=-1/0.002 5［（1-0.002 5×0.194）×（1-0.002 5×0.210）-1］=0.404，采用同样计算方法可得到其它指标集的模糊测度如表5、表6 所示。

Table 4 Index evaluation weight of supplier main body Yj表4 供应方主体Yj 的指标评价权重

Table 5 Fuzzy measure vector of demand-side subject Xi for evaluation index表5 需求方主体Xi 针对评价指标的模糊测度向量

Table 6 Fuzzy measure vector of supplier subject Yj for evaluation index表6 供应方主体Yj 针对评价指标的模糊测度向量

需求方以及供应方具有相同的重要性，所有需求方Xi对供应方Yj评价指标（C1，C2，C3，C4，C5）下的评价值向量为（183，182，184，174，190），则评价指标按照评价值向量从小到大再次排序：交货期、产品价格、技术水平、企业信誉、售后服务。供应方Yj对需求方Xi在评价指标（D1，D2，D3，D4）下的评价值向量为（194，203，195，178），评价指标按照评价值向量从小到大再次排序：生产成本、制造工艺、企业信誉、付款期。根据表5、表6 求得的模糊测度向量以及式（8）、式（9）计算出匹配满意度αij和βij，再由公式（10）计算得到最终满意度如表7、表8 所示。

Table 7 Satisfaction Matrix of Demand Side Xi to Supply Side Yj表7 需求方Xi 对供应方Yj 满意度矩阵αij'

Table 8 Satisfaction matrix of supplier Yj to demander Xi表8 供应方Yj 对需求方Xi 的满意度矩阵βij'

根据公式（10）建立双边匹配模型，根据核心竞争理论由公式（11）分别求得ω1为0.545、ω2为0.454，将其转化为单目标规划模型，使用LINGO 软件求解，得到x16=x23=x32=x44=x55=1，其余xij=0。

本文若不考虑指标间协同效应影响，则依据需求方及供应方的互相评价数据与指标权重相乘求和，可得到综合偏好信息，然后利用公式（9）得到双方满意度矩阵如表8、表9 所示。建立多目标规划模型，同样由公式（11）计算出ω1、ω2，转化为单目标规划模型求解。

Table 9 Satisfaction Matrix α″ij of Demand Side Xi to Supply Side Yj表9 需求方Xi 对供应方Yj 满意度矩阵α″ij

Table 10 Satisfaction Matrix β″ij of Supply Side Yj to Demand Side Xi表10 供应方Yj 对需求方Xi 的满意度矩阵β″ij

求解该模型可得x14=x23=x32=x46=x55=1，其余xij=0。两种匹配结果对比如表11 所示。

Table 11 Analysis of matching results of two methods表11 两种方法的匹配结果分析

通过表11 匹配结果可知，运用两种匹配方法得到的匹配结果有所不同。若考虑指标协同效应，则主体X1与Y6匹配，X2与Y3匹配，X3与Y2匹配，X4与Y4匹配，X5与Y5匹配，这说明在满足用户所需以及柔性制造为目标的云制造资源匹配市场中，考虑指标协同效应对匹配结果有重要的影响，同时也说明本文所提方法的可行性。