Quantitative coherence analysis of dual phase grating x-ray interferometry with source grating∗

Zhi-Li Wang(王志立), Rui-Cheng Zhou(周瑞成), Li-Ming Zhao(赵立明),Kun Ren(任坤), Wen Xu(徐文), Bo Liu(刘波), and Heng Chen(陈恒)

School of Electronic Science&Applied Physics,Hefei University of Technology,Hefei 230009,China

Keywords: x-ray imaging,phase contrast,grating interferometer,fringe visibility

1. Introduction

Over the last two decades, x-ray grating interferometry has attracted increasing attention from the scientific community.[1–13,15–18]As a multi-modal imaging technique,x-ray grating interferometry provides simultaneously three complementary signals,i.e.,attenuation,refraction,and darkfield,from the same set of experimental data.[1–4,11,18]Particularly,standard x-ray tubes are fully compatible with x-ray grating interferometers in the so-called Talbot–Lau geometry.[3,4]Consequently,x-ray grating interferometry has shown significant potential applications in diverse fields including, but not limited to,mammography,[19,20]materials science,[21,22]nondestructive testing,[23]and early detection of lung injury.[24]

In x-ray grating interferometry,a phase grating is always employed to generate an interference pattern at the so-called fractional Talbot distances downstream.[1–4]With a sample placed close to the phase grating, the interference pattern is locally distorted. Analyzing the local distortion of the interference pattern allows one to retrieve the x-ray attenuation, refraction, and dark-field signals on a pixel-by-pixel basis.[1–4,11,17]In order to achieve a high sensitivity,the phase grating typically has a period of a few micrometers. The resulting interference fringes, with a pitch of several micrometers,cannot be directly resolved by common imaging detectors with a typical pixel size of several tens of micrometers. To utilize these detectors, one needs to use an absorbing grating,with its pitch matching that of the interference fringe, placed before the detector to convert the fringe distortion into intensity variations in a Moir´e approach.[1–4]However,the attenuating analyzer grating blocks more than half x-rays transmitting through the sample,which will significantly increase the dose deposition to the imaged sample.

In recent years, dual phase grating x-ray interferometry has demonstrated its attractive advantages.[25–30]Two phase gratings are employed as beam splitters in a dual phase grating interferometer.The split beams transmitting through the phase gratings interfere with each other,creating distinct diffraction orders in the intensity fringe pattern.[27,28]The imaging detector just resolves the beat pattern of large periodicities, and makes other fine patterns a constant background. Compared to x-ray Talbot–Lau interferometers, the dual phase grating interferometers directly resolve intensity fringes without the need of an absorbing analyzer grating. This advantage will lead the radiation dose to substantially decrease in x-ray imaging exams. Moreover,unlike the case of the inverse geometry of Talbot–Lau interferometers,[5]the limitation to the field-ofview can be avoided in dual phase grating interferometers with the total system length kept compact.[25,26]

In dual phase grating x-ray interferometers, spatially coherent illumination of the phase gratings is always necessary to attain a high fringe visibility.[25]However, it is challenging for standard x-ray tubes to provide sufficient spatial coherence and adequate flux simultaneously. Alternatively, inspired by the solution in Talbot–Lau interferometry, one may employ the combination of a large-focus x-ray source with an absorbing source grating.[29]The source grating creates an array of line sources, each of which illuminates the phase grating coherently.[3,4,10,29]In Talbot–Lau interferometry,with the period of the source grating satisfying the Lau condition, the fringes generated by all the line sources in the source grating are superimposed constructively to achieve a good fringe visibility.[3,4,10,31]Similarly,a new generalized Lau condition was derived for dual phase grating interferometer equipped with a source grating.[28]The theoretical results have been validated by simulations and experimental results.[29]However,experimentally measured fringe visibility was no greater than 6.5%, which was too low for potential practical applications.Therefore,it is of great importance to find how the spatial coherence of the x-ray beam affects the fringe visibility in dual phase grating x-ray interferometry. And that is the purpose of this work.

The rest of this paper is organized as follows. In Section 2, we apply the partial coherence theory to dual phase grating interferometry equipped with a source grating. With the generalized Lau condition satisfied, we show that the spatial coherence effect is approximately determined by the source grating profile. In Section 3, we investigate the influence of the source grating profile,including its duty cycle and finite bar height,on the fringe visibility quantitatively. Finally,we conclude this work in Section 4.We hope that those results can be used as guidelines for designing and optimizing dual phase grating interferometers equipped with a source grating.

2. Quantitative coherence analysis of dual phase grating interferometry

Consider a dual phase grating x-ray interferometer as shown in Fig.1, where an absorbing source grating G0 and two phase gratings G1 and G2 are employed. Assuming a quasi-monochromatic illumination and following a quantitative theory of dual phase grating interferometry,[27]we find that the resolvable intensity fringes by the detector can be expressed as follows:where I0is the incident x-ray intensity at G1 plane; µindenotes the spatial coherence degree of the x-rays of wavelength λ incident on G1;[32]sinc(lpD/pfr) represents the pixel-averaging effect, with pDbeing the detector pixel size,and pfr=M5p2/[M1−(p2/p1)] the period of resolvable intensity fringes;anand bsdenote the Fourier coefficients of the grating G1 and G2,respectively; a∗nis the complex conjugate of an; R1is the source-to-G1 distance; R2is the distance between G1 and G2;R4is the G2-to-detector distance; p1is the period of G1,and p2is the period of G2. Note that the relative transverse shift of the gratings G1 and G2 is set to be zero in Eq.(1). The magnification factors used in Eq.(1)are defined as follows:

Fig.1. The schematic diagram of dual phase grating x-ray interferometer equipped with source grating.

In order to employ x-ray sources of large focal spots, an absorbing source grating G0 is introduced into dual phase grating interferometers.[28,29]The source grating divides the tube’s focal spot into an array of virtual line sources. Each of the mutually incoherent line sources can provide spatially coherent illumination of the phase gratings. Since x-ray tubes always have a focal spot much larger than the size of virtual line sources, the effective source intensity distribution can be well approximated by the transmittance function of the source grating,[31]which can be expanded as a Fourier series

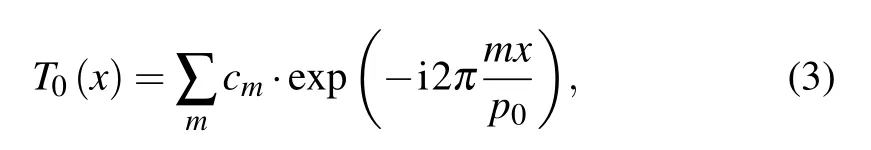
where p0is the source grating period, and the Fourier coefficient cmis given by

with γ0being the duty cycle of the source grating, and T the non-zero transmission through the grating bar. The transmission T is related to the finite bar height h by T =exp(−µt),with µ being the energy-dependent linear attenuation coefficient of the grating material. Under the approximation of Eq.(3),according to the Van Cittert–Zernike theorem,[32]we find that the spatial coherence degree in Eq.(1)is given by

where δ(·) denotes the Dirac delta function. As shown in Eq.(1),the spatial coherence degreeµinrelating to the diffraction order l,represents the reduction of fringe modulation due to partial spatial coherence of x-ray illumination. Therefore,to achieve a high fringe visibility,the spatial coherence degree needs to be maximized. Equation (5) reveals that the spatial coherence degree achieves its maximum value if,and only if,the following geometry condition is fulfilled:

Substituting Eq. (2) and pfr= M5p2/[M1−(p2/p1)] into Eq. (6), we obtain the condition of the source grating period below:

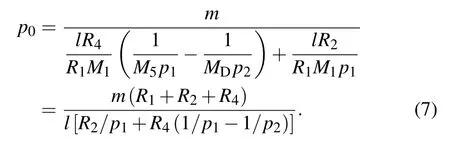
Meanwhile, we note that polychromatic x-ray sources such as x-ray tubes prevail in medical imaging applications. With polychromatic x-rays, the phase grating’s phase shift varies linearly with the x-ray wavelength. Therefore,the fundamental mode (l =1) contributes to the intensity fringe formation for both π-shifting and π/2-shifting phase gratings. With these considerations,we obtain the following unique solution valid for all diffraction order m:

which reproduces the generalized Lau condition for dual phase grating interferometers equipped with a source grating.[28]Note that if the mode is l =−1, the p0given by Eq. (8) just changes its sign,and the source grating configuration remains the same.

With the generalized Lau condition in Eq. (8) satisfied,the spatial coherence degreeµincan be further simplified into the following expression:

which shows that given that the generalized Lau condition is satisfied,the spatial coherence degree is solely determined by the Fourier coefficient of the source grating, i.e. the source grating profile. As shown in Eq. (4), the Fourier coefficient decreases with increasing diffraction order l,reflecting that the fringe modulation decreases with increasing diffraction orders.The higher the diffraction order, the larger the loss in fringe modulation. Substituting Eq. (9) into Eq. (1), we obtain the following expression for the resolvable intensity fringes:

where

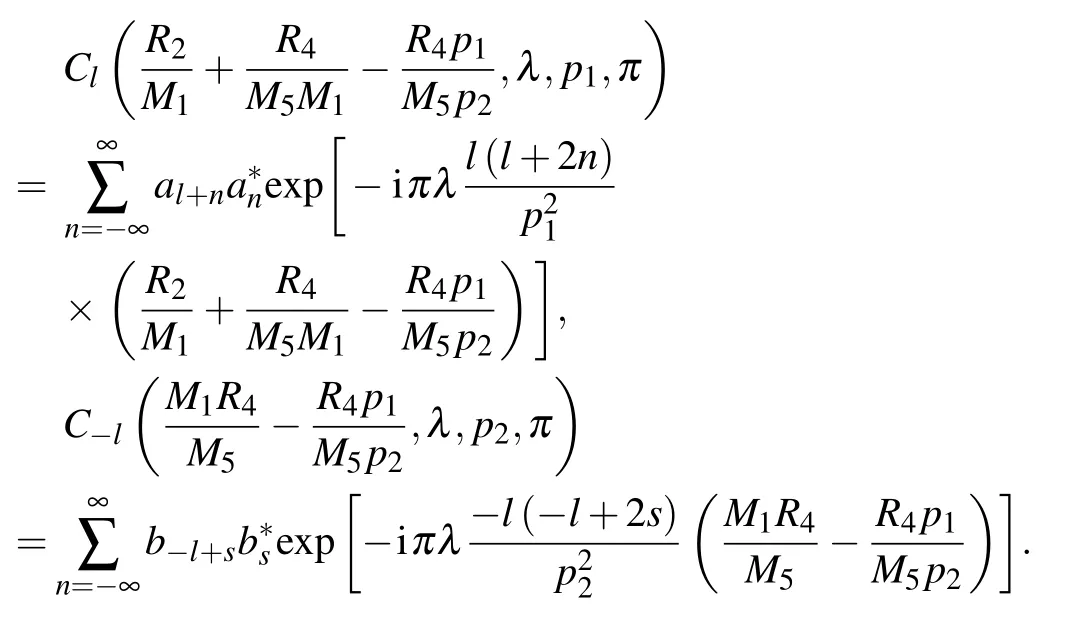
3. Fringe visibility

In x-ray grating-based interferometry, fringe visibility has been a common figure of merit to quantify its imaging performance.[1–4]It is defined as

V =(Imax−Imin)/(Imax+Imin),

with Imaxand Iminbeing the maximum and minimum intensity values,respectively. A high fringe visibility is always required to achieve a high signal-to-noise ratio (SNR) in x-ray grating-based interferometry.[17,18,33,34]As shown in Eq.(10),the visibility of those resolvable intensity fringes is dependent on the x-ray spectrum, the setup geometry, the Fourier coefficients of the source grating and dual phase gratings,and the ratio p1/p2. Since this work aims to investigate the effect of spatial coherence on the fringe visibility,a monochromatic illumination is assumed for further analysis. And the obtained results can be considered to be the upper limit of the achievable fringe visibility for dual phase grating interferometers using polychromatic x-ray sources.

We start with considering an interferometer consisting of two π-shifting phase gratings with a duty cycle of 0.5, to demonstrate how the source grating profile affects the fringe visibility. By use of the closed form expression for the coefficients,[27]we find that Cl=C−l=0 for all odd diffraction orders,and for even integer l,

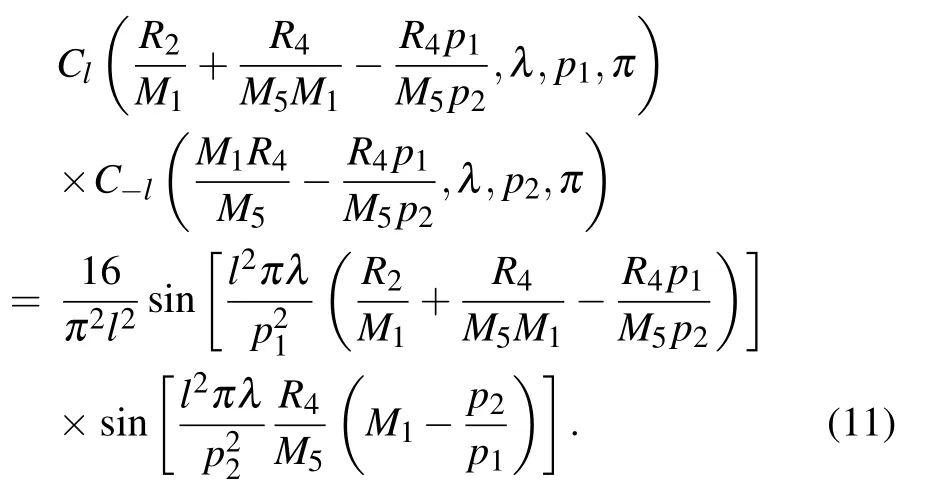
Substituting Eq. (11) into Eq. (10), we find that the coefficients related to the even integer l decrease rapidly with increasing diffraction orders. Thus, in the case of a 0.5 duty cycle, the lowest order (l=2) contributes dominantly to the intensity fringes. Then the expression for the intensity fringe is further simplified into

which shows that the intensity fringe has a period of pfr/2 under monochromatic illumination. From Eq.(12),we find that the fringe visibility is given by

which shows that the fringe visibility is influenced by the source grating profile through c1/c0, the pixel-averaging effect sinc(2pD/pfr),and the setup geometry.

To provide a quantitative insight into the effect of the source grating profile on the fringe visibility, we conduct the following numerical calculations.The considered setup geometry resembles that used for experimental measurements,[29]where λ =4.96×10−11m, p0=24.00µm, p1=4.364µm,p2=4.640 µm, R1=52.79 cm, R2=10.89 cm, and R4=162.34 cm. It can be readily verified that the generalized Lau condition is fulfilled,and that

which means that the fringe visibility is maximized in terms of setup geometry.

Fig.2. Variations of fringe visibility with duty cycle of source grating for dual π-shifting phase gratings(a)(pfr/2)/pD=10 and(b)(pfr/2)/pD=4.

Figure 2 shows the curves of fringe visibility versus duty cycle of the source grating for different values of transmission T and different pixel-averaging effects. The following trends in the fringe visibility can be observed. Firstly, in the ideal case of zero transmission,the fringe visibility decreases monotonically with increasing duty cycle. However, the behavior becomes quite different in the case of a non-zero transmission.As shown in Fig.2,the fringe visibility achieves its maximum,with a duty cycle being 0.25, in the case of 5%transmission.When the transmission increases to 10%,the fringe visibility is maximized,with a duty cycle being 0.3.With the transmission further increasing to 20%,the optimal duty cycle increases to 0.35 where the fringe visibility reaches its maximum. That is, there exists an optimal duty cycle to maximize the fringe visibility in the realistic case of a non-zero transmission.

Secondly, increase in the transmission results in a significant decrease of the maximum achievable fringe visibility. With the transmission increasing from 5% to 10%, the maximum achievable fringe visibility decreases from 0.5928 to 0.4993,i.e.reduces about 16%. In the case of a 20%transmission, the fringe visibility further decreases to 0.3768, i.e.reduces almost 36%.Therefore,the transmission of the source grating bar should be minimized for a high fringe visibility.Taking into account the available x-ray flux that increases with increasing transmission and duty cycles, we can find an optimal duty cycle to maximize the image quality. This subject is left to be investigated in the future.

Finally,a comparison between Fig.2(a)and Fig.2(b)reveals that the pixel-averaging effect has minor effect on the achievable maximum fringe visibility, as long as one fringe period is sampled at least by four detector pixels. This result can be explained by the fact that the term sinc[pD/(pfr/2)]is always greater than 0.9 in real experiments. Meanwhile, we note that the optimal duty cycle that maximizes the fringe visibility is independent of the pixel-averaging effect as revealed by Eq.(13).

Furthermore,we consider an interferometer that consists of two π/2-shifting phase gratings. Again, using the expression for the coefficient Cl,[27]we obtain the following expression for odd diffraction order l:

which suggests that the dominant diffraction order is l =1.Following a similar procedure to that of dual π-shifting phase gratings,we obtain the visibility of the resolvable fringes with a period of pfr,

The analysis of Eqs. (13) and (15) and the results displayed in Fig.3 reveals that the effect of the source grating profile on the fringe visibility is independent of phase grating type,while the pixel-averaging effect shows some little differences due to the different fringe periods. Besides, as a result of the difference in fractional Talbot distances, the setup geometry that maximizes the fringe visibility is changed accordingly.

Fig.3. Variations of fringe visibility with duty cycle of the source grating for dual π/2-shifting phase gratings(a) pfr/pD=20 and(b) pfr/pD=8.

4. Discussion and conclusions

The feasibility of dual phase grating interferometer equipped with a source grating is demonstrated by latest experimental results.[29]However,the measured fringe visibility is quite low compared to typical values of Talbot–Lau interferometry. Therefore, it is important to know how the source grating profile affects the fringe visibility. For this purpose,we apply the partial coherence theory to dual phase grating interferometry equipped with a source grating. The results show that with the generalized Lau condition satisfied, the fringe visibility is influenced by the duty cycle of the source grating and the transmission through the grating bar simultaneously.

In the case of a non-zero transmission, the achievable maximum fringe visibility exhibits a significant decrease with increasing transmission in the source grating. Thus, the bar height of the source grating is required to be large in order to attain a high fringe visibility. On the other hand, for a given transmission, one can find an optimal duty cycle that maximizes the fringe visibility.A comparison between results from dual π-shifting phase gratings and dual π/2-shifting phase gratings shows that the optimal duty cycle is independent of the phase grating used and the pixel-averaging effect. Besides,since the transmission is dependent on the photon energy,special attenuation is required when using a polychromatic x-ray source. In the future work, the theoretical results for some design criteria of dual phase grating interferometers will be evaluated experimentally.

In this work, we present a quantitative coherence analysis of dual phase grating x-ray interferometry equipped with a source grating. In order to attain a good fringe visibility,the geometry is required to satisfy the generalized Lau condition. Furthermore, we derive the fringe visibility formulas for both dual π-shifting phase gratings and dual π/2-shifting phase gratings. Especially,those general expressions given by Eqs. (13) and (15) are applicable to any setup geometry, not limited to the symmetrical one.[27]These results can be used as guidelines for designing the source grating and optimizing dual phase grating x-ray interferometers. Finally,we mention that the presented results can be generalized to the case of a multiline x-ray source.[6]