Evidence of potential change in nonsequential double ionization∗

Changchun Jia(贾昌春), Pu Zhang(张朴), Hua Wen(文华), and Zhangjin Chen(陈长进),‡

1School of Physics and Material Science,Anhui University,Hefei 230039,China

2Department of Physics,College of Science,Shantou University,Shantou 515063,China

Keywords: nonsequential double ionization, quantitative rescattering model, potential change, momentum

1. Introduction

It has been widely accepted that the main mechanisms for non-sequential double ionization (NSDI) are the laserinduced recollision direct ionization(RDI)and the recollision excitation with subsequent ionization(RESI),[1]which can be qualitatively interpreted by the classical three-step rescattering model.[2]In the scenario of three-step model, an electron that was first released by tunneling through the barrier of combined atomic and field potential could then be driven back to the parent ion. Then the laser-induced returning electron may collide with the parent ion, leading to a secondary electron being ionized through RDI or RESI. This implies that NSDI takes place only when the kinetic energy of returning electron is sufficiently high to ionize an electron of the residual ion or to promote this electron to an excited state. According to the classical rescattering model, the maximum kinetic energy that a returning electron can accumulate in the field is 3.17Up,where Upis the ponderomotive energy that is proportional to the laser intensity. This indicates that a“threshold intensity”(the minimum intensity)for NSDI is required. However, NSDI processes have been observed to occur at intensity below the expected threshold intensity in the experimental measurements for both the total yields of doubly charged ions[3]and the correlated two-electron momentum distributions(CMDs)[4]as well.

It was argued[5]that the confliction of the recollision model with experimental observations arises from the assumption that scattering can be treated as if it takes place in a free atom. In a free atom or ion, the total energy of a continuum electron must be positive. Therefore, an incoming electron must possess a kinetic energy larger than the threshold energy for excitation to promote the ground-state electron to an excited state and remain a continuum electron. Nevertheless,this is not necessarily the case when the collision takes place in an electric field.Since the combined electric and atomic potentials form a barrier below zero, the incoming electron can escape from the atom or ion even with negative energy provided that its energy is higher than the potential barrier after the collision. As a result,even when the returning electron has an energy less than the energy difference between the ground state and the excited state, electron impact excitation of the parent ion can still take place in the laser-induced recollision process, since the returning electron can donate more energy to the ionic electron compared to the laser-free collisions.This is somehow equivalent to lowering of threshold,although the energy level of an excited state is not lowered. The lowering of threshold due to the presence of electric field is referred to as potential change(PC)in this paper.

The evidence of PC in NSDI was first provided by van der Hart and Burnett.[5]Using a recollision model, they performed the calculations on the ratio between double and single ionization for He atoms subjected to intense laser pulses. It was shown that by taking the laser field at the recollision into account,the recollision model used in Ref.[5]successfully reproduced the ratio between double and single ionization below threshold intensity.

The methodology proposed by van der Hart and Burnett was recently adopted by Chen and collaborators in the quantitative rescattering(QRS)model.[6]With the PC considered,the QRS model was modified and employed to evaluate the yields of doubly charged ions due to NSDI of He and Ne by intense laser pulses at wavelengths of 800,780,400 and 390 nm,and the obtained results were found to be in good agreement with the experimental measurements over the entire intensity range including the intensities below threshold.[6–8]Very recently,using the modified QRS model,Chen et al.[9,10]simulated the CMD for NSDI of He. It was found that the CMD reproduced by the modified QRS model was in better agreement with the experimental measurements[11]than that predicted by the original QRS model,which confirms again the validity of the modifications made in the QRS model.

While the early measurements of the total yield of doubly charged ions as a function of the laser intensity[12]settled the controversial debate on the mechanisms responsible for NSDI, the measured momentum distributions of doubly charged ions[13]provide more insight into the ionization mechanism and hence offer more stringent test of the theoretical models. In this paper,we apply the QRS model to simulate the longitudinal momentum distributions of doubly charged ions for NSDI of He in 795 nm laser pulses. We make direct quantitative comparisons of our model results with the experimental measurements of de Jesus et al.[14]It turns out that with the PC taken into account,the agreement between theory and experiment is greatly improved, which provides, for the first time,the direct evidence of PC in NSDI above threshold intensity.

Unless indicated otherwise, atomic units (a.u.) are used throughout this paper.

2. Theoretical method

In this paper, we consider PC in the QRS model and investigate the effect of PC on the process of NSDI.

2.1. Potential change in NSDI

Suppose that we have an ion with effective charge Z in an electric field F(t)=F0cos(ωt),the combined electric field and Coulomb potentials along the polarization axis z of the laser field is given by

As displayed in Fig.1,a barrier appears when the electric field is added to the Coulomb potential. The maximum of the barrier in the combined Coulomb and electric field potentials is

For electron impact excitation and ionization of a singly charged ion,Z=1 and 2,respectively.Thus,for laser-induced electron impact excitation and electron impact ionization,the Coulomb potential is lowered by |Vb|. This indicates that, in principle, the laser-induced returning electron with energy Erhas sufficient energy to promote a secondary electron from the ground state to an excited state when

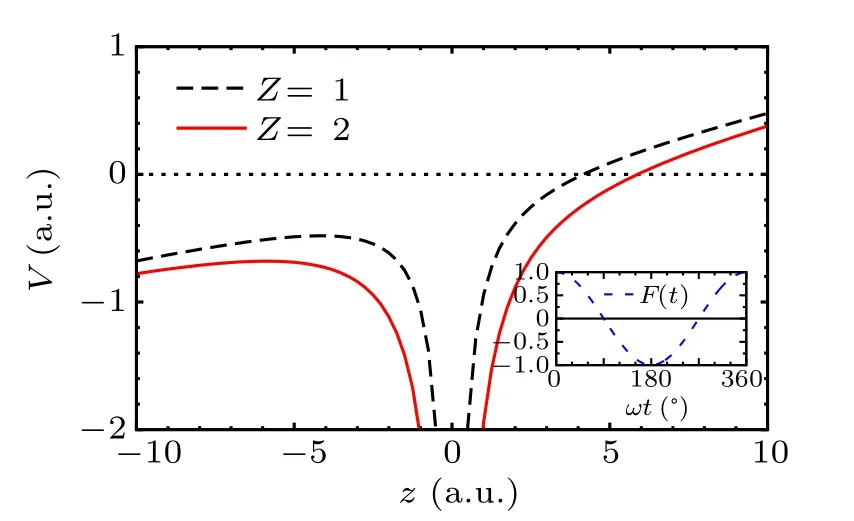
Fig.1. Combined electric field potential F(t) = F0 cos(ωt) and Coulomb potential with Z =1 and Z =2 along the polarization axis z of the laser field at an intensity of 10×1014 W/cm2. The phase of the electric field is chosen to be ωt=290◦.The inset shows the normalized monochromatic laser field.

Although the barrier height can be easily determined, it is far from straightforward to take the PC into account in the QRS model since recollision takes place at different times and the corresponding barrier height of the combined atomic and electric fields varies with the angle to the polarization axis. For simplicity, we choose an “average” returning time of t=290◦/ω in our calculations.[9]Unfortunately,even with this average returning time,it is still a formidable task to perform actual numerical calculations. Alternatively, we follow the prescription suggested by van der Hart and Burnett.[5]To account for the lowering of threshold, we adjust the collision energy so that the laser-free incoming electron energy Eicorresponds to the laser-induced returning electron energy

where j stands for exc or e2e.

2.2. The QRS model for NSDI

We aim to evaluate the longitudinal momentum distributions of doubly charged ions for NSDI of He and compare the simulated results with the corresponding experimental findings.[14]The momentum distributions of doubly charged ions are obtained by projecting the CMD for NSDI onto the main diagonal. Since the details of the numerical procedures for simulations of the CMD for NSDI of helium atoms based on the QRS model have been presented in Refs.[8,9,15],here we only give a brief overview.

The main philosophy of the QRS model for laser-induced rescattering processes is that the momentum distributions for photoelectrons can be expressed as a product of the returning-electron wave packet(RWP)and the field-free scattering cross sections. Therefore, to simulate the CMD for NSDI of He, we first need to prepare the RWP, the tripledifferential cross sections (TDCSs) for electron impact ionization and the differential cross sections(DCSs)for electron impact excitation of He+. The RWP is evaluated based on the improved strong-field approximation for high-order abovethreshold ionization.[16]For the laser-induced recollision processes of He+considered here, only the cross sections for the singlet spin channel should be used, since the two electrons involved in the process start in the singlet ground state of He, and their singlet coupling is preserved.[17]The singlet TDCS for laser-free (e, 2e) of He+are calculated using the BBK model,[18]in which the Coulomb interaction between the two outgoing electrons is accounted for. The singlet DCSs for laser-free electron impact excitation of He+are evaluated using the state-of-the-art multi-electron B-spline R-matrix closecoupling theory[19]for incident energies below 100 eV and the distorted-wave Born approximation[20]for higher energies. In this paper,only the DCSs for excitation to the excited states of n=2 and n=3 are calculated, since the excitation to higher states can safely be neglected based on the n−3scaling law.

With all these ingredients well prepared, we are now ready to simulate the CMD for NSDI of He. In the QRS model,the CMD for RDI and RESI are simulated separately.

Similarly,the CMD for RESI is given by

The magnitude of vector potential Arat the instant of recollision is determined by the returning electron energy,

where Eris given by Eq.(5).

3. Results and discussion

In this study, we focus on the parallel momentum distributions of the doubly charged ions for NSDI of He in 795 nm laser pulses at intensities of 6.0,7.0,10.0,and 12.5×1014W/cm2measured by de Jesus et al.[14]Very recently,we investigated the intensity dependence in NSDI of He by strong laser pulses at 800 nm,[23]which is very close to the wavelength considered in the present work. In Ref.[23],the CMD for NSDI of He at intensities in the range from 2×1014W/cm2to 15×1014W/cm2have been simulated without taking into account PC,and the ingredients involved in the CMD,including the scattering cross sections for laser-free electron impact excitation and electron impact ionization,the parallel momentum distributions for the projectile electron after recollision and the tunneling-ionized electron have been presented. Here,we therefore only show the parallel momentum distributions for the two correlated electrons and the doubly charged ions.

In Fig.2,we plot the simulated CMD and the corresponding parallel momentum distributions of the doubly charged ion for RESI and RDI in NSDI of He by 795 nm laser pulse at an intensity of 10×1014W/cm2. First of all,it is obvious that PC plays an important role in producing the CMD for both RESI and RDI. By comparing Figs. 2(c) and 2(d) with Figs. 2(a)and 2(b), one can see that, with the PC effect taken into account,the CMDs for both RESI and RDI shrink such that the density in the CMD at smaller momenta increases. This is due to the fact that, according to Eqs. (5) and (8), the outgoing electrons in the recollision processes at a given incident energy are supposed to possess smaller drift momenta when the lowering of potential barrier is considered. As a result,as demonstrated in Figs.2(e)and 2(f),in the parallel momentum distributions of He2+, more probabilities for RESI at smaller momenta are generated and the‘valley’predicted by the original QRS model is almost filled. At the same time,the double peak in the distributions of RDI moves towards the center.

From Fig.2,one can also see that,with the PC accounted for, the total yields for both RESI and RDI increase. Nevertheless,the relative increase for RDI is more pronounced than that for RESI since the PC for RDI is much larger than that for RESI. Take the peak intensity of 10×1014W/cm2as an example, the maximum adjustments of the collision energy for the returning electron are 37 eV for RDI and 13 eV for RESI.

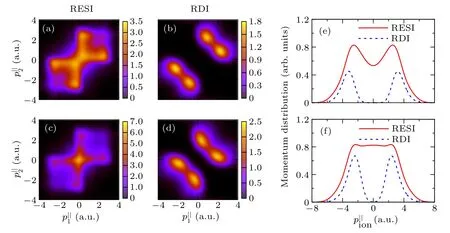
Fig.2. Correlated two-electron momentum distributions for RESI and RDI in NSDI of He by a 795 nm laser pulse at an intensity of 10×1014 W/cm2 [(a)–(d)]and the corresponding parallel momentum distributions of the doubly charged ion[(e),(f)]. The results without and with the potential change accounted for are shown in the first and the second rows,respectively.

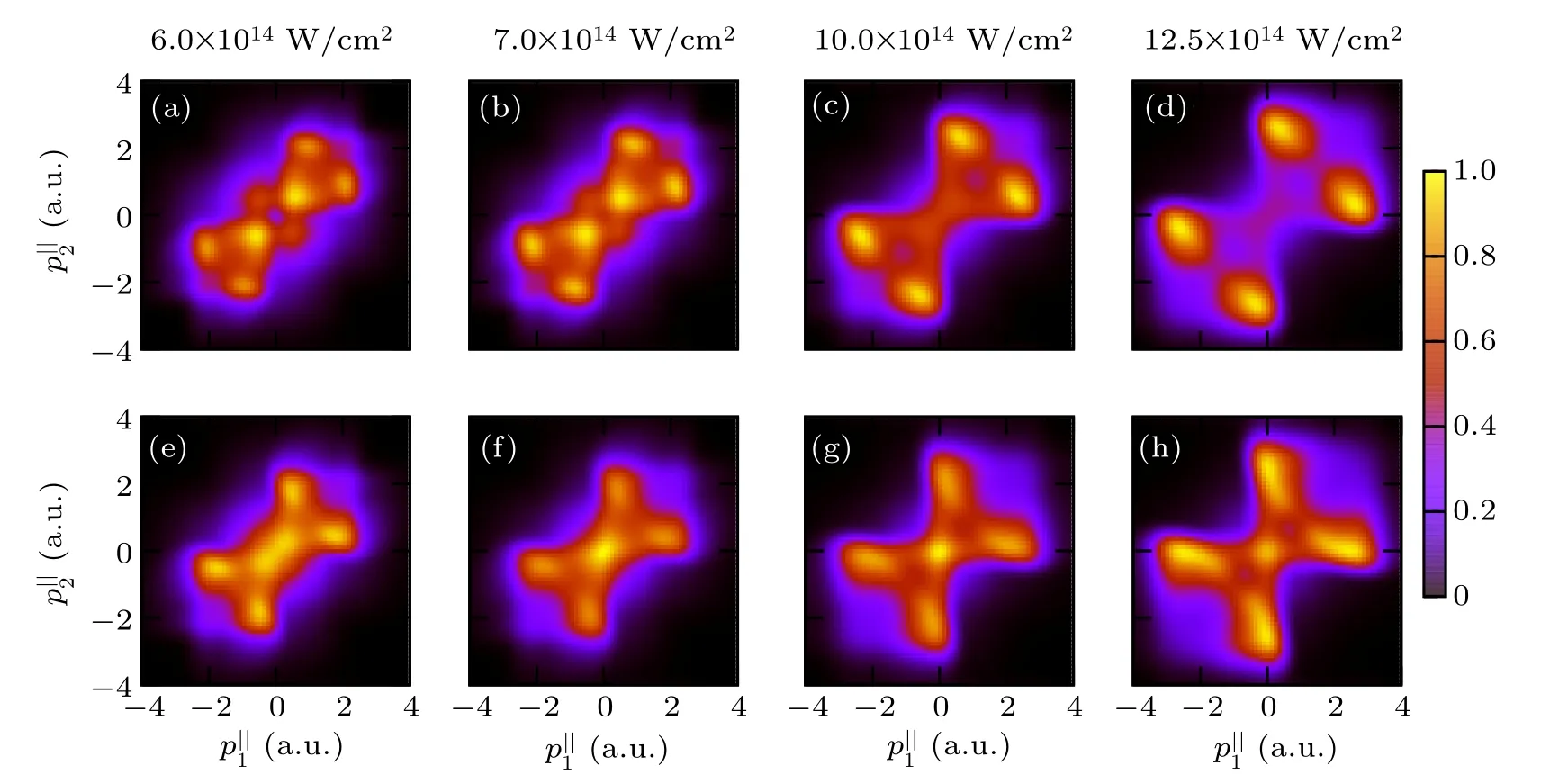
Fig.3. Normalized correlated two-electron momentum distributions for NSDI of He by 795 nm laser pulses at intensities of 6.0,7.0,10.0,and 12.5×1014 W/cm2. The results without and with the potential change accounted for are shown in the first and the second rows,respectively.

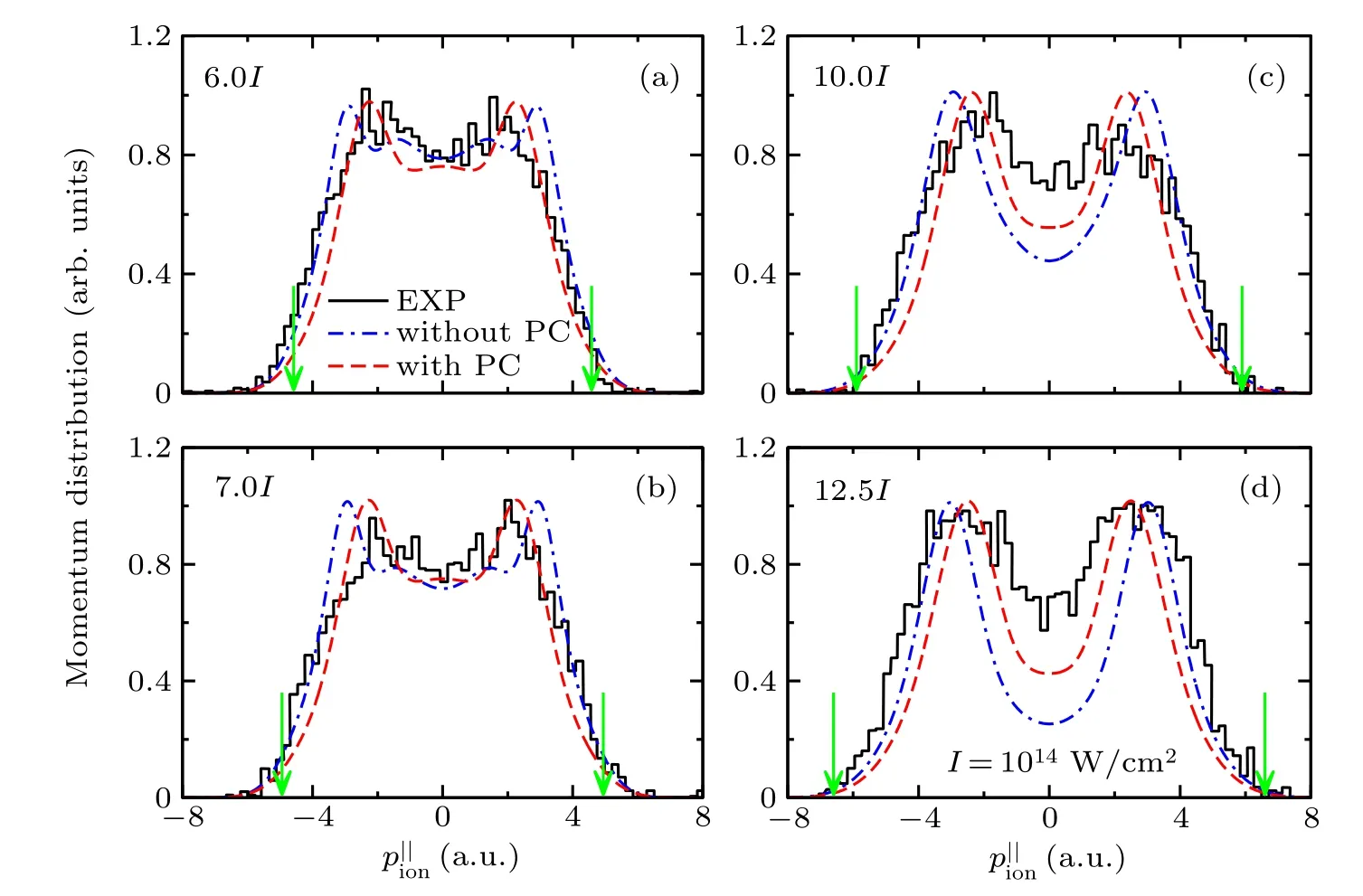
Fig.4. Parallel momentum distributions of doubly charged ions for NSDI of He by 795 nm laser pulses at peak intensities of(a)6.0,(b)7.0,(c)10.0, and(d)12.5×1014 W/cm2. The black solid line represents the experimental data taken from de Jesus et al.,[14] the blue chain and red broken curves are the simulated results without and with the potential change accounted for. The arrows indicate the upper limits for thekinematically favored ion momenta of±4.

By adding the CMD for RESI to that for RDI,we obtain the entire CMD for NSDI.The CMD for NSDI of He,including both RESI and RDI,by 795 nm laser pulses at intensities of 6.0,7.0,10.0,and 12.5×1014W/cm2are displayed in Fig.3.As is expected,the region of the CMD spreads as the intensity increases and,at a given intensity,the CMD is squeezed when the PC is considered. Furthermore,it should be noted that the maximum energy of the returning electron is proportional to the laser intensity. At 12.5×1014W/cm2,which is the highest intensity considered here,the maximum energy of the returning electron is about 235 eV. As demonstrated in Ref. [23],close to threshold, the total cross section for ionization increases rapidly until it reaches a maximum below 120 eV,and then decreases very slowly with increasing impact energy. On the other hand,the total cross section for excitation decreases steadily beyond a narrow maximum within about 15 eV above the threshold energy. Around 150 eV, the two cross sections become comparable. Therefore,the relative contribution from RDI is enhanced with the increase of intensity. This explains why the momentum distributions in the outer part in the first and third quadrants become denser at higher intensities.

Finally,we emphasize that in all the simulated results presented in this paper,the focal volume averaging has been considered.

4. Conclusions

Using the QRS model with and without taking into account the potential change due to the presence of electric field at the instant of recollision,we have simulated the parallel momentum distributions of doubly charged ions for NSDI of helium by 795 nm laser pulses at intensities of 6.0, 7.0,10.0 and 12.5×1014W/cm2. The model results are compared directly with the corresponding experimental measurements. It is found that when the potential change is considered, the width between the two peaks becomes narrower and the minimum at zero momentum increases. Both of these changes in the simulated ion momentum distributions improve the agreement of the model results with experimental findings.The present investigations provide clear evidence of potential change in NSDI at intensities above the threshold.

We comment that, besides the total yields of the doubly charged ions measured at intensities below the threshold intensity,[5–7]the potential change effect has also been observed in the experimental measurements of CMD at intensities above the recollision threshold.[10]Although the CMD provides more detailed information than the longitudinal momentum distribution of doubly charged ions, direct quantitative comparisons between theory and experiment are hampered due to the two-dimensional data of CMD.In this sense,we believe that to show the direct evidence of potential change effect in NSDI above-threshold intensity,the one-dimensional longitudinal momentum distribution is the best candidate.