A local refinement purely meshless scheme for time fractional nonlinear Schr¨odinger equation in irregular geometry region∗

Tao Jiang(蒋涛), Rong-Rong Jiang(蒋戎戎), Jin-Jing Huang(黄金晶), Jiu Ding(丁玖), and Jin-Lian Ren(任金莲)

1School of Mathematical Sciences,Yangzhou University,Yangzhou 225002,China

2Department of Mathematics,University of Southern Mississippi,Hattiesburg,MS 39406-5045,USA

Keywords: Caputo fractional derivative, nonlinear Schr¨odinger/Gross–Pitaevskii equation, corrected smoothed particle hydrodynamics,irregularly domain

1. Introduction

In recent years, fractional differential operators have a wide range of applications in engineering and science because they can accurately describe the complex dynamic behaviors in the real world, such as the viscoelasticity procedure, the fluid mechanics, the electrostatics, and other physical events.[1–9]Moreover, the integer nonlinear Schr¨odinger equation is usually used to describe some physical phenomena in quantum mechanics,[10–16]in which the Gross–Pitaevskii equation (GPE) is one of the most important nonlinear Schr¨odinger equations. As the fractional calculus receives more and more attention, fractional quantum mechanical phenomena have been discovered in the literature[17,18]and then the fractional nonlinear Schr¨odinger equation has become an important equation for describing the fractional quantum mechanical character.[5,19–25]Subsequently, some fractional nonlinear Schr¨odinger equations (FNLSE) have been studied for different mechanical properties.[19]Although the theoretical analysis for fundamental fractional Schr¨odinger equations is still being carried on, it is very difficult to obtain analytical solutions for most of FNLSEs[5,26–30]Hence,the design of a highly-efficient and accurate numerical method to find approximate solutions for FNLSEs is necessary and important in practice. Presently, many kinds of numerical methods[23–27,31–42]have been proposed for the numerical solutions of time fractional nonlinear Schr¨odinger equations(TF-NLSEs), such as the finite difference method (FDM), finite element method(FEM)and local discontinuous Galerkin(LDG)method, etc.The purpose of this paper is to study the TF-NLSE numerically.

Meshless techniques have gradually attracted researchers’attention and been extensively applied to various PDEs,[43–53]because the meshless method does not need mesh generation or reconstruction required in grid-based methods. There are some common meshless methods,[43–47,51,52]such as the conventional SPH (TSPH),[47]corrected SPH(CSPH),[47–50]EFG,[51,52]MLS,[43]RBFs,[44,46]MLPG,[53]FPM, RKPM,[52]etc. Although the above meshless methods have been widely used to simulate various fluid/solid mechanical problems,[47,51,52]the meshless technique is rarely used for the TF-NLE.[46,50,53–55]As a purely meshless particle TSPH or CSPH method without completely depending on grids has been extensively used for many kinds of fluid dynamic fields,[47–50,56–65]it has not yet been applied to TFNLSEs to the best of our knowledge. The CSPH has higher accuracy and better stability than the TSPH,and it is easier to implement in programming than other meshless methods(for example the EFG,MLPG,RBFs,etc.).

For the above reason, the main aim of the present paper is to propose a hybrid scheme (named LRCSPH-FDM which is a local refinement corrected SPH method coupled with FDM) for 2D TF-NLSEs in a complex region with irregular geometry by combining the FDM for the Caputo time fractional derivative[66]and the CSPH[50,59]with a new kernel function[63]for spatial derivatives. Meanwhile, the local refinement particle technique is also adopted to reduce the numerical error, and the parallel technique[50,59]is introduced to enhance the computational efficiency. To further demonstrate the capability of the proposed LRCSPH-FDM, the numerical solutions of the challenging time fractional Gross–Pitaevskii equation (TF-GPE) with a potential and a rotation term in an irregularly shaped domain is investigated by the present LRCSPH-FDM. It is worth noting that the main idea of this work has much more progress than that in Ref. [51].There are three main differences as follows. First, this work focuses on the time fractional nonlinear Schr¨odinger equation(TF-NLSE) which is different from the time integral nonlinear Schr¨odinger equation in Ref. [51]. There is a wide range of application in physics, where the TF-NLSE can be used to describe many quantum phenomena[67]but the time integral nonlinear Schr¨odinger equation cannot. Also, the merits of corrected SPH(which was easily used in irregular complex domains but can be locally refined if need be)are not described well or sufficiently in Ref.[51].This paper emphasizes the particle characteristics of SPH, so the simulation domain can be locally refined in any areas if need be. Then the SPH scheme can be used in various complex domains (see Fig.1)which are not simulated in Ref. [51]. Last but not least, the time fractional derivative is much more difficult to obtain than time integral derivative.In L1−2 scheme.[66]The results of all former time steps are needed to simulate the current result,but to simulate the integral results only one former time step result is used. So,this method needs to occupy more memory spaces when time increases than that in Ref. [51]. The MPI parallel technique is used in 2D examples to enhance the computation efficiency. In a word, this work simulates the time fractional nonlinear Schr¨odinger equation in complex domains and the merits of LRCSPH-FDM are demonstrated through the examples.

The rest of this work is organized as follows. The 2D TF-NLSE/GPE with initial/boundary conditions is described in Section 2. The proposed particle scheme for 2D TF-NLSEs based on the local refinement CSPH and FDM is given in Section 3. Section 4 demonstrates the numerical convergence of the proposed method for 2D TF-NLSEs with different cases of the particle distribution in a rectangular or irregularly shaped domain. An extended application of the proposed particle method for 2D TF-NLSE/GPEs in regular/irregular domains is illustrated and discussed in Section 5. Section 6 gives some remarks and conclusions.

2. Time fractional nonlinear Schro¨dinger equation

We consider the time fractional nonlinear Schr¨odinger equation(TF-NLSE)[46]

with the initial value condition u(x,0)=w(x)and the boundary value condition

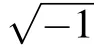
There are several definitions of fractional derivatives, among which the Riemann–Liouville and Caputo fractional derivatives are two of the most used ones in fractional calculus(see Refs. [1,27,46]). In this paper, we use the Caputo fractional derivative.

The Caputo fractional derivative of order α is defined as

So the Caputo time fractional derivative of order α (0 ＜α ＜1)takes the form

Also,the Caputo fractional derivative satisfies

The Gamma function Γ(z)is

where z is in the complex domain,and has the following properties:

(i)Γ(z+1)=zΓ(z),

(ii) for any n ∈N, the set of positive integers, Γ(n) =(n−1)!,

3. Local refinement approximate scheme(LRCSPH-FDM)

3.1. Scheme for time fractional derivative

At present, two approximation schemes for the Caputo time fractional derivative have been proposed and used widely to solve time factional differential equations,which are called the L1 method with o(τ2−α)-order[4–9]and L1 −2 method with o(τ3−α)-order,[66]respectively. Here,the L1−2 scheme is adopted.

Taking the 1D case, let the positive integers M and Nbe given,set the time step τ=T/M and the space step h′=L/N,and define the space nodes xi=ih′with 0 ≤i ≤N and the time nodes tn=nτ with 0 ≤n ≤M.Then the L1−2 formula for the Caputo fractional derivative(5)[1]can be obtained as follows:

where 0 ≤j ≤k −1,and for k ≥2

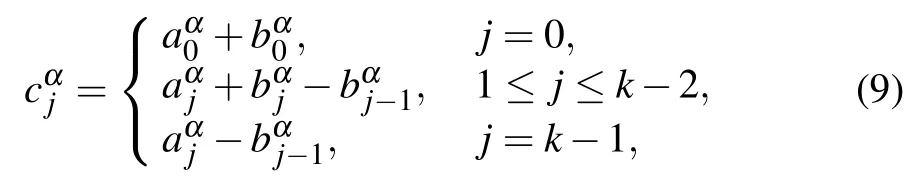
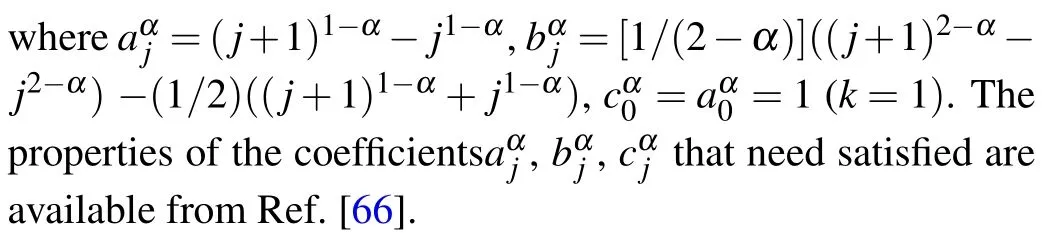
3.2. CSPH scheme for space derivatives

3.3. Conventional SPH scheme

In the conventional SPH simulation, the kernel function[47–50]is first used for integral interpolates. Secondly,the simulated domain Ω is discretized into a finite number of particles by the SPH method,[47]where each particle has its own physical quantities such as the density,mass and the temperature, which depend on the problem solved. Finally, the integral form of the kernel function is approximately obtained by the particle discretization.

The integral representation of the function u(x) and the derivative of the function ∇u(x) at the point x = (x,y) can be obtained by the kernel function W and the kernel function derivative ∇W as follows:[47,50]

In this paper,the double cosine smoothing function[63]is considered as

W(R,h)

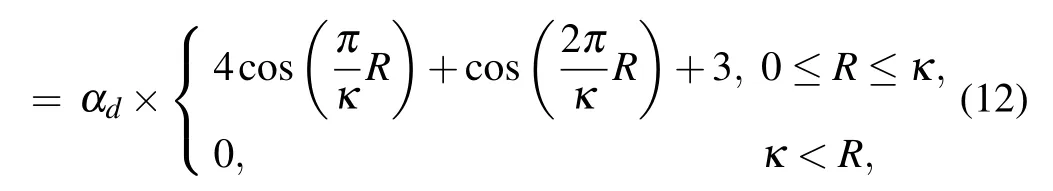
where Wij=W(|xi−xj|,h), ∇iWij=∂W(|xi−xj|,h)/∂xi,and ∇iWijsatisfies ∇iWij=−∇jWij. The positive integer Nirepresents the neighbor particle number within the support domain of particle i.

3.4. Corrected SPH scheme

There have arisen the problems with low accuracy and instability[47,49,56]as the conventional SPH method is used near the boundary of the domain, or in the case of irregular particle distributions.Some improved SPH methods have been proposed to enhance the numerical accuracy and stability by using the Taylor expansion.[47–50,56]A corrected SPH(CSPH)scheme for the first-order derivative with two-order accuracy without kernel derivatives has been proposed in Refs.[59,62],which can perform well even in the region of non-uniform particle distributions.[50]So far, the above CSPH has not been used to solve the fractional differential problem to the best of our knowledge. In this work, the CSPH scheme combining the FDM scheme(8)is used to approximate the TF-NLSE(1),in which the space derivative of Eq. (1) is discretized by the CSPH.Then,the conventional SPH scheme(14)for the firstorder derivative can be corrected as

For the second-order derivative ∂2u/∂x2i,it is firstly discomposed into two first-order derivatives. Secondly,the above corrected scheme(15)for the first-order derivative is adopted continuously to approximate the above second-order derivative. That is,

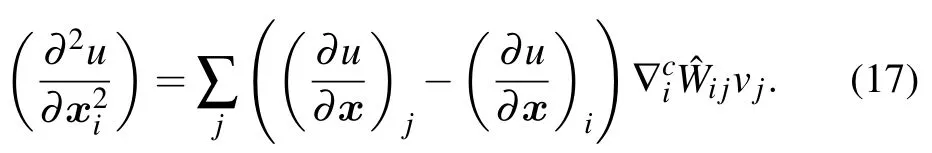
From the above procedures, it can be seen that neither the CSPH scheme (15) nor the CSPH scheme (17) involves kernel function derivative, which offers some advantages over other improved SPH methods.[59,62]Also, the CSPH method has a better flexibility than a class of grid-based methods(e.g.,FDM)due to its own special advantages,for example,an easy implementation of simulations in the case of non-uniform particle distributions or irregular computing domains. In other words, the local refinement approach is suitably and easily implemented for reducing the numerical error in the present particle method,but it is complicated in the grid-based methods. And then the local refinement particle distribution technique is applied to the boundary and specified parts of the computing region when the CSPH scheme(15)combined with the FDM scheme (8) is proposed for the TF-NLSE, named the “LRCSPH-FDM” scheme. The above viewpoints will be demonstrated in the following (Section 4) by the numerical simulation for several examples,involving the numerical convergence rate and the flexibility of the proposed method. It is regrettable that a strictly unified theory of the particle method has not been developed well[47,52,56]due to the influence of some empirical theory parameters.

To show the calculation process of the LRCSPH-FDM scheme directly,the flowchart is as follows.

Input: The simulation domain Ω (the locally refined domain and the irregular particle distributions areas);the discrete particle numbers N;computation time T;the space step h′;the time step τ; the simulation function u; the kernel function W and its smoothing length h;some physical quantities for particles;the coefficient a,b,c of L1−2 scheme.

Output: The approximated solution u(xj,T).

The detailed algorithm flow:

Step 1The simulated domain Ω is discretized into N particles and for each particle xj(j=0,1,...,N −1),its neighbor particles are marked.It is noted that Ω has various particle distributions(see Fig.1)and some of them are difficult to simulate by the grid-based method. Meanwhile, to enhance the computation accuracy,the local refinement scheme is used.

Step 2Assign the physical quantities for each particle xj.The initial data are assigned to u(xj,t=0).

Step 3The first-order derivative ∂u/∂xjis approximated by formula(15)(combined with formula(16)),noting that the boundary conditions are not considered here.

Step 4Use the result in Step 3 as the initial value, then the second-order derivative

is obtained by using formula(15)repeatedly.

Step 5The first and second-order derivative on the righthand side are achieved by Steps 2–4(corrected SPH)and the L1−2 scheme(FDM)is used to approximate the time derivative on the left-hand side,the next time step result is obtained to be u(xj,t1). Update the results on the boundaries with the boundary conditions.

Step 6The temporal loop(from Step 3 to Step 5)is continuously implemented until the required computation time is achieved and then the result u(xj,T)is output.

Moreover,the parallel technique based on the MPI communication is adopted to enhance the computational efficiency in the programming with C++,which is detailed in our pervious researches.[50,59]

4. Numerical accuracy and convergence of LRCSPH-FDM

In this section,the convergence rate and the flexibility of the proposed LRCSPH-FDM for the TF-NLSE are shown by the numerical demonstration. Three 1D/2D examples[31,36,46]with Dirichlet or periodic boundary conditions are considered in a regular or irregular particle distributed region(see Fig.1).The L2-norm error and convergence rate are defined as

where ujrepresents the numerical solution,Ujis the exact solution, and d01and d02are two different initial particle distances.

Fig.1. Sketches of all computational regions with different particle distributions in the whole numerical solvers.

It is worth noting that figure 1 shows the sketches of all particle distributed cases in regular or irregular computing domains in the whole numerical solvers of Sections 4 and 5.Panel 1(a) shows the case of uniform particle distribution in a rectangular domain. Panels 1(b)and 1(c)display two cases of non-uniform particle distributions in rectangular domains,involving the local refinement case of panels(b). Panels(d)–(f)are for the cases of non-uniform particle distributions in irregular computing regions,which are obtained by the Abaqus software.

Example 1 (1D TF-NLSE)We consider the 1D TFNLSE

with the periodic boundary value condition u(0,t)=u(1,t)=it2,t ∈[0,1]and the initial value condition u(x,0)=0. The source term f(x,t)is

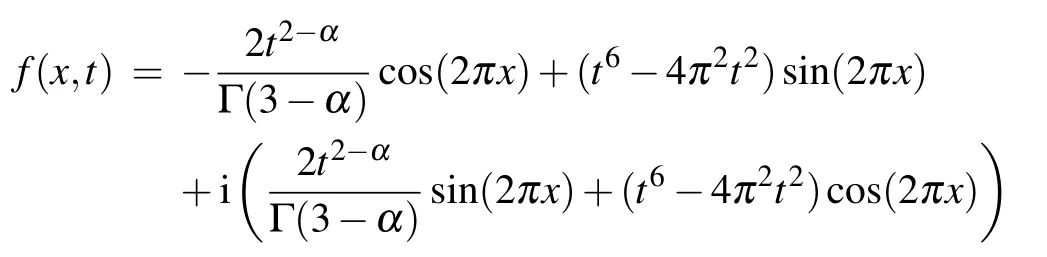
and the exact solution is u(x,t)=t2(sin(2πx)+i cos(2πx)).

where functions f1(x,t), f2(x,t)are

The above equations have the computing domain [0,2π]and the analytical solution is u(x,t)=t2(cosx+i sinx), and v(x,t)=t2(cosx+i sinx). The initial data and the boundary condition can be obtained by the above theoretical solution.

Through the simulations of Examples 1 and 2, the numerical convergence rate and the flexibility of the proposed method for the 1D TF-NLSE are shown in Figs. 2 and 3 and Tables 1 and 2. Figure 2 shows the changes of curves Re(u)and Im(u)obtained by the present method for Example 1 with α =0.7 at different times. The particle number N =41 and time step dt =1.0×10−4. The present numerical results including the real and imaginary part of u accord well with the analytical solutions. As the time increases, the real part expands in the sinusoidal form and the imaginary part expands in the cosine form. The error (e2) and convergence rate (Cr)of the modulus, real and imaginary part of u obtained by using the proposed method for Example 1 (α =0.7 at t =1)are demonstrated in Table 1,and the advantage of local refinement particle distributions is illustrated in Table 2. It can be seen that the proposed method has almost second-order numerical accuracy for solving the 1D TF-NLSE (see Table 1).In Table 2,the local refinement regions[0,0.1]and[0.9,1]are set to be the initial particle distance d0=1/80, and the other region is set to be d0=1/40. The error of the local refinement case is obviously smaller than that of the coarse case at different times. For the proposed purely meshless particle method,the local refinement technique can be easily implemented in simulation and it can enhance the numerical accuracy without adding more calculations. To further investigate the accuracy and ability of the proposed method for the 1D TF-NLSE,the 1D coupled TF-NLSE of Example 2 with two interacting nonlinear packets is simulated as indicated in Fig.3. It is accurate to capture the interaction between two nonlinear waves by the proposed method,and the evolution of the wave function versus time is also accurately simulated.

In a word,the proposed purely meshless method is accurate and flexible for solving the 1D TF-NLSE.

Next, the numerical convergence rate and flexibility of the present method for the 2D TF-NSLE problem are demonstrated by the following simulation of Example 3 in rectangular or irregular computing domains.

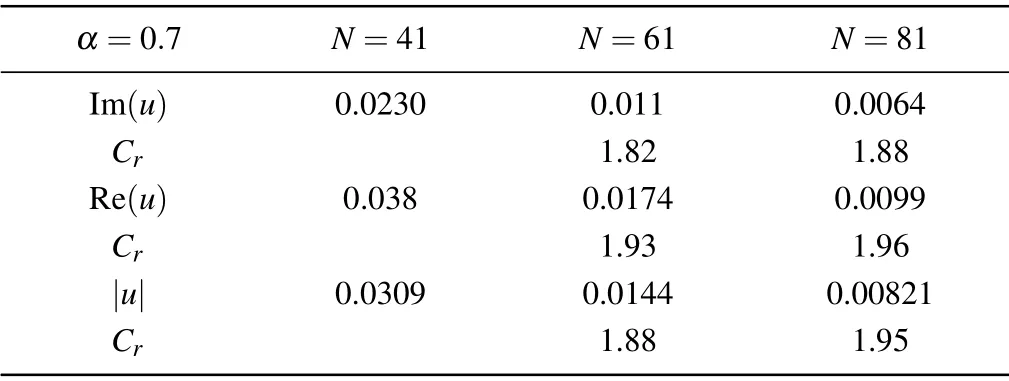
Table 1. Values of error(e2)and convergence rate(Cr)of the modulus,real and imaginary parts of u obtained by the proposed method for Example 1 with α =0.7 at t=1.

Fig.2. Changes of curves of Re(u)and Im(u)obtained by the present method for Example 1 with α =0.7 at different times.

Table 2. Comparison of errors (e2) of |u| obtained by the proposed method between two particles’ distributions of coarse case and local refinement case for Example 1 with α =0.7 at different times.

Example 3 (2D TF-NLSE)Consider the 2D timefractional nonlinear Schr¨odinger equation

with the nonlinear term

The analytical solution u(x,y,t)=t3(cos(x+y)+i sin(x+y))in the rectangular region(x,y)∈[0,1]×[0,1]or in the irregular region(panels(e))in Fig.1 is considered in this subsection.The initial data and boundary condition can be achieved by the above exact solution.

In the simulation of Example 3 with α =0.7,the particle distributions of panels(a),(b),and(c)in Fig.1 in the rectangular region and the particle distribution panel(e)of Fig.1 in the irregular one (which is obtained by the Abaqus software)are all used to show the accuracy and the extended flexibility of the proposed method for the 2D TF-NLSE (see Figs. 4–6 and Tables 3 and 4). Meanwhile, the advantage of the purely meshless particle method over the gird-based method(e.g., FDM) is also obviously demonstrated. The curves of the real and imaginary part of u(0.3,y) obtained by the proposed method for Example 3 with α=0.7 at t=0.2 are shown in Fig.4. The present numerical results accord well with the exact solution. The numerical convergence rate and computing errors of the proposed method for the 2D TF-NLSE with particle distributions [panels (a) and (b) in Fig.1] are illustrated in Tables 3 and 4, respectively. From Figs. 4–6 and Tables 3 and 4, we can obtain that (i) the proposed method has a numerical accuracy of about 1.8 for the 2D TF-NLSE;(ii) the present method is accurate and can be flexibly used to simulate the 2D TF-NLSE with non-uniform particle distributions(panels(b)and(c)in Fig.1)in rectangular regions or an irregular domain (panel (e) in Fig.1); (iii) the local refinement technique in the proposed method is feasible and efficient([0,0.2]×[0,0.2],[0.8,1.0]×[0,0.2],[0,0.2]×[0.8,1],[0.8,1]×[0.8,1],[0.4,0.6]×[0.6,0.8]are the local refinement regions);(iv)the contour of the wave in the 2D TF-NLSE with non-uniform particle distributions can be exactly obtained by the proposed purely meshless method.

Table 3.Values of error(e2)and convergence rate(Cr)of modulus,real and imaginary parts of u obtained by the proposed method for Example 3 with α =0.7 at t=0.2.

Table 4. Comparison of error(e2)of|u|obtained by using the proposed method between two particle distribution cases of panels(a)and(b)in Fig.1 for Example 3 with α =0.7 at different times.

Fig.4. Curves of(a)real and(b)imaginary parts of u(0.3,y)for Example 3 with α =0.7 at t=0.2.

Fig.5. Contours of non-uniform particle distribution panel(c)of Fig.1 obtained by using the proposed method for Example 3 with α =0.7 at t=0.1:(a)Re(u)and(b)Im(u).

Fig.6. The contours of the particle distribution panel(e)of Fig.1 obtained by using the present method for Example 3 on an irregular region with α =0.7 at t=1: (a)Re(u)and(b)Im(u).

To sum up,the proposed particle method has a better numerical accuracy for the 2D TF-NLSE with non-uniform particle distributions panels (b) and (c) in Fig.3, and a stronger flexibility in extended applications than the FDM for the 2D TF-NLSE in complex domains with an irregular geometry.

5. Numerical investigation for 1D/2D TF-NLSE

In order to further demonstrate the ability and flexibly extended application of the proposed purely meshless method for the TF-NLSE, three classical 1D/2D examples without theoretical solutions are considered and investigated by the present method,and compared with the FDM results.

Example 4 (1D TF-NLSE)Consider the 1D time fractional nonlinear Schr¨odinger equation

with the initial value condition u(x,0)=u0(x)and the boundary value condition u(x,t)→0(|x|→∞). The external potential function V(x)=0,the nonlinear term f(|u|2)u=2|u|2u+|u|4u includes general nonlinear effects on u, and the initial data u0(x)= e−3(x−2)2+e−3(x+2)2.

Fig.7. Comparison between curves of |u| versus x, obtained by different methods for Example 4 with α =0.7 at two different times.

Fig.8. Evolution of wave|u|with time,obtained by the present method for Example 4 with(a)α =0.7 and(b)α =0.95.

To verify the reliability of the present method for Example 4, figure 7 illustrates the comparisons between |u| values obtained using different methods for Example 4 with α =0.7 at two different times.The present numerical results are closer to the FDM results,which indicates that the proposed method is credible for predicting the wave change versus time in the 1D TF-NLSE.The evolution of wave|u|versus time,obtained by the present method for Example 4 with two different α values,is shown in Fig.8.Figure 9 shows the curve of wave|u|at t =0.2 with α =0.7 and α =0.95 for showing the difference in nonlinear wave between two different fractional parameters.From Figs. 8 and 9, we can find that i) the crest of the wave decreases as time goes on;ii)it is reliable to predict the evolution of nonlinear waves in the 1D TF-NLSE by the proposed method; iii) the fractional parameter has an important influence on the wave movement; iv) a larger peak value of wave|u|is achieved when the parameter α increases.

Fig.9. Waves |u| obtained by the present method for Example 4 at t=0.2 with two different α values.

Example 5 (2D TF-NLSE)Consider the 2D timefractional nonlinear Schr¨odinger equation with a periodic condition,which is

and the initial data u(x,y,0)=(1+sinx)(2+siny). The periodic size along the x direction and along the y direction are both 2π.

The case of Example 5 with α =1(time integral order)is usually considered to illustrate the extended application and the robustness of a numerical method for the NLSE,which can be seen in Ref.[68]. Figure 10 shows the wave|u|obtained by two different methods for Example 5 at t =0.108 with α =1(time integral order)and α =0.7(time fractional order). The initial particle distance d0=1/60,time step dt =2.0×10−5and β =1. To illustrate the difference in result between integral time derivative and fractional time derivative, figure 10 displays the results for time derivative changing with time.The result at t=0 is the initial result,while figure 10(a)shows the result with time integral order (α =1) and figure 10(b)displays the result with time fractional order(α =0.7)when t=0.108. From the results,it can be seen that there is a sharp wave with high value when α=1 and when the time derivative changes to α =0.7(time fractional derivative), the evolution is quite different. In Fig.10(b), it turns out to be two small waves. To demonstrate these results, in this work the results from the FDM are compared with those from the LRCSPHFDM.It is clear that the present numerical results are in agreement with the FDM results,which indicates that a)it is reliable to predict the wave propagation with a periodic boundary condition by the present method;b)the fractional parameter has a significant influence on the wave change in the 2D TF-NLSE;c)the singularity can be obviously observed whenα =1,and it is weakened when α =0.7(see Fig.10(b)).

Fig.10. Waves|u|obtained by using different methods for Example 5 at t=0.108 with(a)α =1(time integral order);(b)α =0.7(time fractional order).

Example 6 (2D TF-GPE)Consider the 2D time fractional Gross–Pitaevskii equation with a rotating term

with the initial data

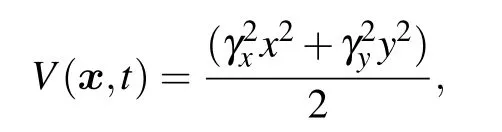
and the other parameters γx=γy=1.0,Lz=0.7,and β2=1.0.

Fig.11. Comparison of waves |u(0,y)| obtained by different methods for Example 6 with α =0.7.

Fig.12. Contours of wave |u| obtained by the present method for Example 6 for particle distribution panels (d) of Fig.1 with α =0.7 at different times: (a)t=0,(b)t=0.3,(c)t=0.6,and(d)t=1.

Fig.13. Contour of wave|u|obtained by the present method for Example 6 for particle distribution panel(f)of Fig.1 with α=0.7 at t=0(a),0.3(b),0.6(c),and 1.0(d).

Here,three different computing regions of panels(a),(d)and(f)of Fig.1 in Example 6 are considered to further illustrating the flexibility of the proposed method for the 2D TFGPE.The size of the computing region can be observed from Figs.11–13. The comparisons of curves of wave|u(0,y)|obtained by using different methods for Example 6 in a rectangular domain with α=0.7 are first demonstrated in Fig.11 to show the reliability of the present method for the 2D TF-GPE.And then the proposed particle method is used to investigate the evolution of wave|u|of Example 6 in irregular regions of panels(d)and(f)in Fig.1 with α =0.7 as the time increases,which are illustrated in Figs. 12 and 13. From Figs. 11–13,it can be seen that i) the present results accord well with the FDM results in Fig.11;ii)the peak values decreases with time in the case of the regular or irregular domain;iii)the proposed method can be flexibly extended to the 2D TF-NLSE/GPE in a complex irregular domain.

To sum up,it is reliable to predict the propagation of nonlinear waves by the present particle method for the 1D/2D TFNLSE;the proposed method has more widely extended applications in the simulation of 2D problems in irregular computing regions than the grid-based method.

6. Remarks and conclusions

A flexible, effective, and accurate hybrid scheme (a local refinement corrected SPH method combined with FDM,which is called “LRCSPH-FDM”) by combining a corrected SPH for spatial derivatives and the FDM scheme for the Caputo time fractional derivative is first proposed to solve the 2D time fractional nonlinear Schr¨odinger equation(TF-NLSE)in regular or complex irregularly shaped domains. Subsequently,the proposed purely meshless method is extended to predict the quantum mechanical character governed by the time fractional Gross–Pitaevskii equation(TF-GPE)in regular or complex irregular domains. Several examples are simulated by the present method and the results are compared with analytical solutions or FDM results. Meanwhile, the local refinement technique is adopted to reduce the numerical error, and nonregular particle distribution in rectangular or complex irregularly shaped domains is considered to demonstrate the flexible application ability and the merits of the purely meshless CSPH method for the TF-NLSE.Through the above numerical tests we can draw some conclusions below.

(I)The proposed method for the TF-NLSE has a secondorder numerical accuracy, and it is reliable for simulating the TF-GPE without theoretical solutions.

(II) It is flexibly and easily implemented to simulate the TF-NLSE/GPE in non-uniform particle distributions or in complex irregularly shaped domains by the present method.

(III)The local refinement particle distribution can reduce errors and has a lower computational quantity than the global refinement approach.

(IV) The quantum mechanical property in the GPE can be effectively and accurately predicted by the proposed purely meshless method.