Complex coordinate rotation method based on gradient optimization∗

Zhi-Da Bai(白志达), Zhen-Xiang Zhong(钟振祥), Zong-Chao Yan(严宗朝), and Ting-Yun Shi(史庭云)

1State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics,Wuhan Institute of Physics and Mathematics,Innovation Academy for Precision Measurement Science and Technology,Chinese Academy of Sciences,Wuhan 430071,China

2University of Chinese Academy of Sciences,Beijing 100049,China

3Department of Physics,University of New Brunswick,Fredericton,New Brunswick E3B 5A3,Canada

4Center for Cold Atom Physics,Chinese Academy of Sciences,Wuhan 430071,China

Keywords: complex coordinate rotation method,resonant state,metastable state,gradient optimization

1. Introduction

Resonant states play an important role in atomic,molecular, and nuclear physics and have a long history of research,such as doubly-excited states in two-electron systems,[1,2]Efimov states in weakly bound few-body systems,[3,4]resonance phenomena under Debye plasma environment,[5]four-body resonant states in positronium hydride[6]and positron-helium,[7]resonances in positron scattering by atoms and molecules,[8]metastable states in antiprotonic helium ¯p4He+,[9–11]and resonance phenomena in nuclear physics.[12,13]

There exist many theoretical methods for studying resonant states. In early years, the S-matrix[14]and R-matrix[15]theories were used to solve resonant problems. In 1970s, the method of complex coordinate rotation(CCR)was mathematically established,[16]and was first used in studies of scattering involving three charged particles by Raju and Doolen.[17]After that, the CCR method was further developed to calculate atomic resonant states by Ho.[18]From then on, the CCR method has been widely adopted as a powerful tool for investigating resonant states in atoms and molecules, including its application to high-precision antiprotonic helium spectrum.[10,11]On the other hand, Feshbach in 1962[19]formulated a general theory for studying resonances, where the wave function space is partitioned into closed- and openchannel segments.The hyperspherical close-coupling method,developed by Lin[20]in 1984 to calculate doubly-excited states, was applied to positron–atom scattering.[21]Recently,the stabilization method combined with hyperspherical coordinates and B-spline expansion was applied to positron–atom scattering by Han and co-workers.[22]Among these methods,both the CCR method and the closed-channel approximation of the Feshbach theory can reach high precision for long-lived metastable states with small widths, such as 10−11atomic units in ¯p4He+decaying via a radiative channel.[9]However,an Auger-dominated state in ¯p4He+is usually short-lived and possesses a width larger than 10−10atomic units,[9]such as the (N =31, L=30) state, where N and L are, respectively,the principal and total angular momentum quantum numbers.The accuracy of the closed-channel approximation of the Feshbach theory is limited by the width of a resonant state,[23]whereas the accuracy of the CCR method can go beyond this limit,[10]making the CCR method more suitable for shortlived metastable states.

Since the variational approach using Hylleraas- or Sturmian-type basis sets has been proven to be effective in dealing with atomic or molecular few-body systems,it is natural to combine these basis sets with the CCR method,[24–27]and solve resonance problems variationally. However, due to the lack of extreme theorem for a resonance state,historically it is common practice in using the CCR method that the nonlinear variational parameters in the trial wave function are optimized through repeated trial and error manual adjustment,which could become extremely laborious and inefficient, especially for a high-dimensional parameter space. In this work,we propose a novel approach of complex coordinate rotation based on the gradient optimization(CCR-GO).The advantage of the CCR-GO method over the existing resonance methods is that it does not require manual adjustment of nonlinear parameters in the wave function;instead,a mathematically welldefined optimization path can be followed, leading to a resonance pole quickly. Our method will be tested for various three-body atomic systems.

2. Computational method

In the method of complex coordinate rotation,[18]under the radial coordinate transformation r →rexp(iθ), the original Hamiltonian of the system ˆH = ˆT + ˆV, where ˆT and ˆV are,respectively,the kinetic and potential energy operators,is transformed into

where the rotational angle θ is assumed to be real and positive. According to the Balslev–Combes theorem,[16]in the complex energy plane, for sufficiently large θ this transformation rotates the continuum spectrum of ˆH to “expose” the resonant poles around the thresholds from the unphysical sheet to physical sheet of the Riemann surface,and the bound state poles remain unchanged on the negative side of the real axis.The eigenenergies can be obtained by solving the following complex eigenvalue problem:

where the eigenfunction Ψθis square integrable and the corresponding discrete complex eigenvalue E =Er−iΓ/2 defines the position Erand the width Γ of a resonance. By choosing a basis set {ψn,n=1,...,N} in an N-dimensional Hilbert space,the complex eigenvalue problem(2)can be converted to the following generalized algebraic complex eigenvalue problem:

In our CCR-GO approach,we try to minimize either

or

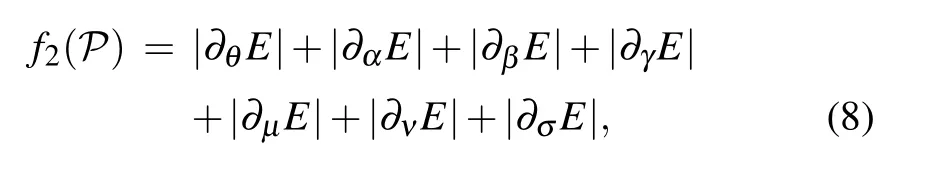
where P ≡(θ,α,β,γ,µ,ν,σ) aggregates all variational parameters,such as the rotational angle θ and the nonlinear parameters α, β, γ, µ, ν, and σ that appear in Eq. (6), for example. The optimization procedure for minimizing f1(P)or f2(P) can be done iteratively from step k to step k+1:[P]k→[P]k+1,where the initial values of optimization parameters, as well as the search directions and steps for each parameters,are determined by the Broyden–Fletcher–Goldfarb–Shanno algorithm,[34]or the quasi-Newton method. In particular,the search directions are directly related to the following vectors:

where ∇=(∂θ,∂α,∂β,∂γ,∂µ,∂ν,∂σ) is the gradient operator in the full parameter space.It is noted here that,for an efficient search of a resonant state,the rotational angle term|∂θE|must be included in the optimization procedure, whereas the other parameters can sometimes be optional except for some broad resonant states.

3. Results and discussion

For the purpose of demonstrating the effectiveness of our optimization technique, figure 1 shows the convergence pattern for the lowest S-wave resonant state in Ps−using only one set of nonlinear parameters in Eq.(6),with the initial values θ=α=β =γ=µ=ν=σ=0.2 and the size of basis set N =252. One can see from the figure that,starting from the same initial point,the two optimization paths based on g1(E)and g2(E) approach each other rapidly around the resonant pole after about 9 iterations. Of course, further iterations are needed if one wishes to obtain higher accuracy, as shown in Table 1. It is noted that,since the resonance width of this state is relatively small,the searching process is less sensitive to the initial values of nonlinear parameters and the searching paths.For narrow resonant states, the optimization of nonlinear parameters can be performed firstly to minimize the real energy eigenvalue when θ =0. After this process,the results are only limited by the width of the resonant states.[23]These optimized parameters as the initial values of CCR-GO implementation can avoid the spurious solutions efficiently and converge to the right results. The prior optimization of real energy can also reduce the computation load and enhance the rate of convergence. However, for a resonant state of broad width, the above strategy for searching the initial values is invalid due to the shallower minimum in parameter space. Thus, manual adjustment of the initial nonlinear parameters is required to approach the true lowest position through minimizing the energy derivations as small as possible. It is advisable to use the more demanding condition g2(E)to do searching,instead of g1(E) which is difficult to trap the iteration of parameters into the shallower minimum. It is also noted that our CCRGO method is applicable not only to resonant states, but also to bound ones. Figure 2 shows two optimization paths determined by g1(E)and g2(E)for locating the ground state of helium,with the initial values θ=α=β =γ=µ=ν=σ=0.2 and the size of basis set N =252. The ground-state energy,thus obtained after 30 iterations,is accurate to about 9 digits.

Fig.1. Two optimization paths based on g1(E)and g2(E)for the lowest resonant state 1Se in Ps−below the Ps (N =2) threshold, with the size of basis set N =252. The inset is an enlarged view of the paths around the convergence point. Atomic units are used.

Fig.2. Two optimization paths based on g1(E) and g2(E) for the ground state of helium, with the size of basis set N =252. The inset is an enlarged view of the paths around the convergence point. Atomic units are used.

Table 1. Resonance parameters (Er,Γ/2) for various three-body Coulombic systems. In the table, N is the size of basis set controlled by parameter Ω. A comparison with some of the best theoretical results is also presented. Atomic units are used.

4. Summary

To sum up,we have presented a new approach called the CCR-GO method, which for the first time makes the search for resonance mathematically automated.This is in sharp contrast to the traditional way of manual adjustment of variational parameters. Therefore, our method can greatly improve the search efficiency and search accuracy of resonance poles.Resonance phenomena exist ubiquitously in physics. The significance of our method is by no means limited to few-body atomic systems;it can also be applied in principle to find resonance poles in many areas of physics,including nuclear and elementary particle physics.

Acknowledgment

ZXZ would like to thank V.I.Korobov of JINR for providing his computer codes of complex nonlinear parameters.