Analysis and implementation of new fractional-order multi-scroll hidden attractors∗

Li Cui(崔力), Wen-Hui Luo(雒文辉), and Qing-Li Ou(欧青立)

Hunan University of Science and Technology,Xiangtan 411201,China

Keywords: fractional order,hidden attractor,hidden bifurcation,basins of attraction,circuit implementation

1. Introduction

In recent years,the chaotic system has attracted extensive attention and conducted in-depth studies by researchers due to its particularities. It has promising prospects of many applications in random signal generators,[1–4]synchronous control technology,[5]image processing,[6]secure communication,[7,8]and artificial neural networks.[9–11]The increase in the complexity of the chaotic system and the generation of complex chaotic attractors have brought about the difficulty of deciphering the information in encryption systems.At present,the use of the multi-scroll or multi-wing topology method to improve the complexity of the chaotic system has become a hot topic.[12–14]

Although fractional differential has a history of over 300 years,its application to physics and engineering has been only in the last few decades. In the last three decades, it has been discovered that when we use fractional calculus to describe complex systems, the physical significance becomes clearer and its expression becomes more concise. The nature and behavioral characteristics of an object are revealed with greater ease when we use fractional calculus to characterize the object. Hence,fractional calculus has been gaining increasingly more attention,and its application to engineering and physics has become a research hotspot. As a generalization of the integer number system, fractional calculus can describe the dynamic characteristics of the system more accurately with higher nonlinear complexity, and it has a unique historical memory function. There are mainly two kinds of chaotic attractors: self-excited attractors and hidden attractors. The dynamic characteristics of hidden attractors are completely different from those of self-excited attractors. In recent years,Leonov et al.[15,16]discovered hidden attractors in Chua system and proposed the concept of hidden attractors. At the same time, Leonov provided a new set of numerical analysis methods to find hidden attractors. As is well known, the Lorenz attractor,the Chen attractor,and the Chua attractor are all typical attractors in the traditional sense. However,the researchers in Refs.[17,20]indicated a kind of attractor different from these traditional attractors, namely, hidden attractor.Some of these hidden attractor systems possess no equilibrium points,and some have only a stable equilibrium point with an infinite number of equilibrium points. These are reports on integer-order hidden attractor systems. There are few reports on fractional-order hidden attractor systems.

The integer-order chaotic system has been extended to the fractional-order chaotic system by introducing the fractional-order differential operators based on the mathematical model of the integer-order chaotic system in the early stage of their studies, such as the fractional-order Lorenz system,[21]fractional-order Jerk system,[22]fractional-order Chua system.[23]The fractional-order multi-scroll chaotic system has been widely concerned because it can increase the complexity of the system and the accuracy of chaos.[24–27]In recent years, the hidden chaotic attractor system has also received extensive attention.The searching for the hidden attractors and the hidden bifurcations of the hidden attractor chaotic system has also become a hot topic.[28–30]In Ref.[31]the hidden attractor and the hidden bifurcation phenomenon of the multi-scroll Chua’s chaotic system are studied. In Ref. [32]studied are the chaotic property,quasi-periodicity,and coexistence of hidden attractors in a new simple of four-dimensional(4D) chaotic system with hyperbolic cosine nonlinear terms.In Ref. [33] conducted is a dynamic analysis of the multistable chaotic system of hidden attractors. In Ref.[29]studied are the hidden and transient chaotic attractors in the attitude system of four-rotor UAVs. In Ref.[34]studied are the multistability,hidden chaotic attractors,and transient chaotic analysis of brushless DC motors.

The Riemann–Liouville (RL) derivative and the Caputo derivative are often used in research for practical applications.In the time–frequency domain transformation method, as defined by RL,the integer is used to fit the fractional-order and the fractional-integral operator in the time domain is transformed into a transfer function in the frequency domain and then the piecewise linear approximation method for the frequency domain is used to perform an approximate calculation. The corresponding expanded form can be obtained by solving the system function in the frequency domain. On the other hand, one starts from the Caputo derivative and derives the predictor–corrector method as the time-domain solution method of fractional differential equations. Using the Adams–Bashforth predictor formula and the Adams–Moulton corrector formula can obtain the time series of the system’s corresponding order, thus solving the fractional differential equation. In this paper the definition of Caputo fractional calculus is adopted.

In the present study,we first propose a three-dimensional quadratic fractional-order multi-scroll hidden chaotic attractor system with sinusoidal nonlinear terms. Then we use the Adomian decomposition algorithm[35]to solve the proposed fractional-order chaotic system,thereby obtain the 0.99-order chaotic phase diagram as well as the Lyaponov exponent spectrum, bifurcation diagram, SE complexity, and basins of attraction of the system. In the process of analyzing the system,it is found that the system possesses the dynamic characteristics of hidden bifurcations. Finally, we construct a circuit system of the fractional-order chaotic system by designing an equivalent circuit module of the fractional-order integral operators, thus realizing the 0.9-order multi-scroll hidden chaotic attractors.

2. New fractional-order multi-scroll chaotic system

In this paper a new fractional-order multi-scroll chaotic system with sinusoidal nonlinear terms is proposed. The dimensionless equation of the state is given as follows:

When the parameters of the system(1)are taken as A=8,B=4,C=4,w=3.8,q=0.99(0 ＜q ＜1),the initial value is(1,1,0),the system presents a multi-scroll chaotic state. The Adomian decomposition algorithm is used to solve the system(1). The corresponding system phase diagram is obtained and the results are shown in Fig.1. The analysis in Fig.1 clearly shows that there are hidden attractors in the phase diagram.

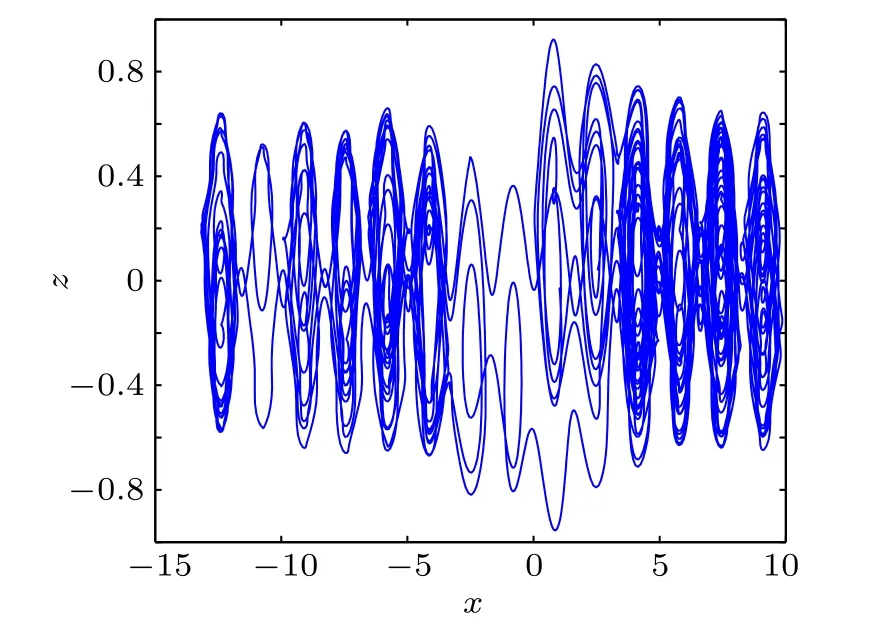
Fig.1. Phase diagram of x–z plane with q=0.99 for q=0.99 initial value(1,1,0).

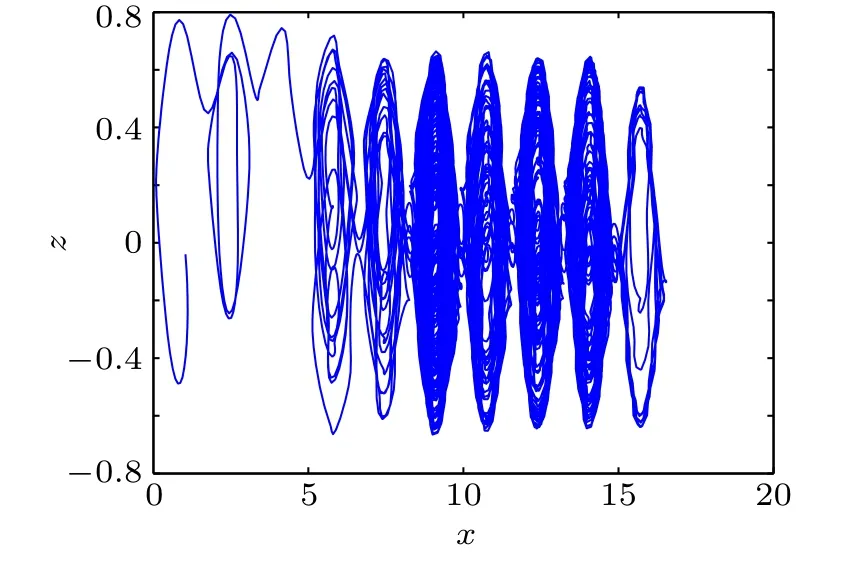
Fig.2. Phase diagram of x–z plane with q=0.9 for q=0.9, initial value(1,1,0).

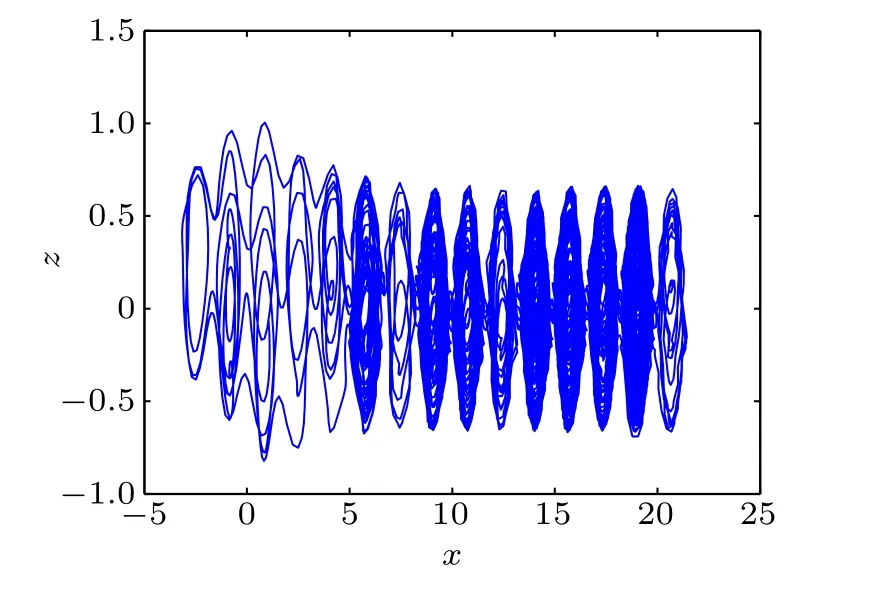
Fig.3. Phase diagram of x–z plane with q=0.8 for q=0.8, initial value(1,1,0).

When the values of q are 0.9 and 0.8, the phase diagrams of system(1)are shown in Figs.2 and 3, respectively.In this paper, the proposed 0.99-order fractional-order multiscroll hidden attractor system is particularly analyzed.

2.1. Equilibrium point and Lyapunov analysis

The equilibrium points of system(1)can be obtained by solving the following equation

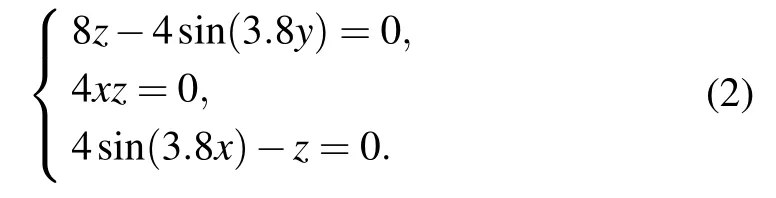
By solving Eq. (2), it is found that the proposed system(1)has infinitely many equilibrium points. As the number of scrolls is affected by sinusoidal function and different initial values,the number of scrolls,which also depends on the order of fractional order, is generated randomly. When q=0.99,the Lyapunov exponents of system (1) are LE1=4.3271,LE2=−0.0542,and LE3=−5.3292,indicating that the system is a multi-scroll hidden attractor system. The Lyapunov exponents are shown in Fig.4.

Fig.4. Lyapunov exponent spectra of system(1)for q=0.99,initial value(1,1,0).

2.2. Bifurcation and Lyaponov exponent spectrum analysis

We set the fractional parameters to be q=0.99, B=4,C=4,and w=3.8,the control parameter A of the system(1)to change from 0 to 10,the initial values of the system(1)are chosen as follows:

x(0)=1, y(0)=1, z(0)=0,

and the step size of parameter A is chosen as 0.01. The bifurcation of the fractional-order multi-scroll system is shown in Fig.5(a). When the fractional-order multi-scroll system is 0.99-order,the system(1)presents a chaotic state varying with time. When the control parameter B increases from 0 to 5,the fractional-order multi-scroll system enters into the chaotic state with period-doubling bifurcations. When the control parameter C increases from 0 to 5, the system (1) has hidden bifurcations, because when the corresponding Lyaponov exponent spectrum enters into the positive exponent state, the bifurcation of the parameter C does not appear but directly enters into the chaotic state,so it is believed that the system(1)has hidden bifurcation behaviors. The Lyapunov exponent of the system(1)is calculated and the corresponding index map is obtained based on the predictor–corrector (PECE) method of Adams–Bashforth–Moulton type and Wolf’s method.

Fig.5.(a)Corresponding bifurcation diagram of state variable A;(b)spectra of Lyapunov exponent,with A changing from 0 to 10.

Obviously,the Lyapunov spectrum provides the parameter ranges of the system(1)when it is in a chaotic state. These ranges are consistent with the results of the bifurcation analysis. As shown in Fig.5(b),there is a positive Lyapunov exponent in a range of 0 ＜A ≤10,indicating that the system(1)is chaotic. As shown in Fig.6(b),the system(1)shows a quasiperiodic state in a range of 0 ＜B ≤1,the system(1)presents a quasi-periodic state. When the parameter B continues to increase to 5, there is a positive Lyapunov exponent, this indicates that the system(1)enters into a chaotic state. As shown in Fig.7, when Z is in a range of 0.06 ＜C ≤5, the system is in a chaotic state. However,the analysis of the corresponding bifurcation diagram shows that the system does not enter into the chaotic state, nor has the bifurcation behaviors in a range of 0 ＜C ＜1,indicating that the system(1)has hidden bifurcation behaviors.

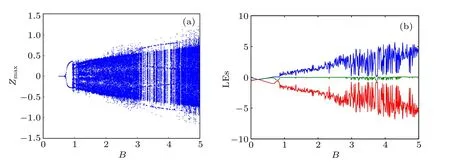
Fig.6. (a)Corresponding bifurcation diagram of state variable B;(b)spectra of Lyapunov exponent,with B changing from 0 to 5.

Fig.7. (a)Corresponding bifurcation diagram of state variable C;(b)spectra of Lyapunov exponents,with C changing from 0 to 5.

Fig.8. (a)Corresponding bifurcation diagram of state variable w;(b)spectra of Lyapunov exponents with w changing from 0 to 5.

2.3. SE complexity analysis

The complexity analysis of the system involves many fields. Scholars have studied these fields and have different understandings of the complexity of the system. So far,there is no unified definition of the complexity. The complexity of the chaotic system refers to the randomness of chaotic sequences. The greater the complexity, the closer to a random sequence the sequence is and the higher the security of the corresponding system. The complexity of the chaotic system,in essence,belongs to the complexity of the chaotic dynamics.So far,many complexity algorithms have been applied to measuring the complexity of the chaotic system, including multiscale entropy,[36]Shannon entropy,[37]fuzzy entropy,[38]and spectral entropy (SE) algorithm.[39]Compared with other algorithms,the SE algorithm has the advantages of few parameters and high precision. Therefore,it is used in this paper to measure the complexity of the chaotic system. In addition,the SE algorithm based on chaotic mapping can provide a better basis for the parameter selection in practical applications.

First, it can be known from Figs. 9(b) and 9(d) that the darker the color, the greater the complexity of the system is,indicating that if the value of the system parameter is within this range, the security of the system is higher. Then it can follow from the analysis of Figs. 9(a) and 9(c) that because system (1) is a hidden attractor system, darker colored areas are randomly distributed in lighter-colored areas and its complexity is affected not only by the orders but also by the initial values of the system. The randomness of the chaotic sequence is dependent on initial values.

Fig.9. Chaos diagrams of fractional-order chaotic system(1)in(a)q–A plane,(b)q–B plane,(c)q–C plane,and(d)q–w plane.

2.4. Basins of attraction

Fig.10. Basins of attraction of coexisting attractors on x(0)–y(0)plane with q=0.99(a),0.98(b),0.9(c),and 0.8(d).

To further study the nonlinear dynamic behaviors of system (1), in this paper we propose using the Lyapunov exponents to calculate the basins of attraction of the chaotic system,because the Lyapunov exponents describe the orbit of the chaotic system. The Lyapunov exponents refer to the average quantities related to the contraction and expansion of the phase space near the orbit in different directions. No matter what sense of space or time they are in,Lyapunov exponents are not local quantities.Each Lyapunov exponent is the average quantity of the local deformation of the phase space relative to the motion of the system. At the same time, it is determined by the long-term evolution of the system. Therefore,the positive Lyapunov exponent is compared with the Lyapunov exponent with the middle value equal to 0 to describe the coexistence of multiple attractors of the chaotic system with different initial value.

The basins of attraction of system (1) can be obtained by changing the parameter q and the initial conditions x(i)and y(i) in a range of (−5, 5) with the system parameters unchanged[40–44]as shown in Fig.10. The red area refers to the basins of attraction of infinity attractors,namely,the point set where the trajectory is diverged. The yellow area refers to the basins of attraction of chaotic attractors, showing the coexistence of multiple attractors. The blue area refers to the periodic area. The red, blue and yellow areas are mixed to form a meshed basin, indicating that there is a smooth and invariant subspace containing the chaotic attractor system(1)(Ref.[40]). Different color areas represent completely different initial conditions, showing the multiple stability of coexistence. The simulation results show that system (1) has a multi-stable phenomenon, namely, the coexistence of multiple attractors. Therefore,the trajectory of the system not only depends on the initial conditions of system(1),but also is related to the fractional-orders. The lower the order, the higher the complexity of the chaotic system is and the larger the red area,which is consistent with the conclusion of the complexity analysis. The partially enlarged diagram of the basins of attraction of the 0.99-order system(1)is shown in Fig.11.

If the basins of attraction of the chaotic system can effectively form a meshed area for each attractor, it will result in the intermittent phenomena of continuous communications between chaotic attractors. The trajectory of the attractor will jump from one attractor to another and then hover around a certain chaotic attractor for a while, thus repeating the cycle continuously.

Fig.11. Enlarged part of basins of attraction with q=0.99.

3. Circuit implementation

Fig.12. Schematic diagram of circuit designed from system(1).

To verify the chaotic characteristics of the fractionalorder chaotic system in the physical sense, a 0.9-order fractional-order multi-scroll chaotic system is designed based on the method of designing integer-order chaotic circuits and the frequency domain approximation method[45]by using resistors, capacitors, capacitors, and other devices, including the analog operational amplifier TL082,the multiplier AD633.The power supply voltage is±12 V.In this paper designed is an analog circuit to implement the 0.9-order fractional-order multi-scroll chaotic system. The schematic circuit diagram and its parameters are shown in Fig.12. The fractional-order unit circuit with 0.9-order is shown in Fig.13.

Its parameters are Ra= 63 MΩ, Rb= 1.6 MΩ, Rc=0.0158 MΩ, Ca=0.44 µF,Cb=0.49 µF,Cc=0.3 µF. The values of these resistances are determined in accordance with the parameters of the fractional-order multi-scroll system(1).The chaotic attractors are observed with an oscilloscope. In this paper,provided are the chaotic attractors of the x–z plane displayed by the digital oscilloscope used in the actual environment as shown in Fig.14. It is shown that the numerical simulation result of the fractional-order multi-scroll system(1)is consistent with the result of the circuit implementation.

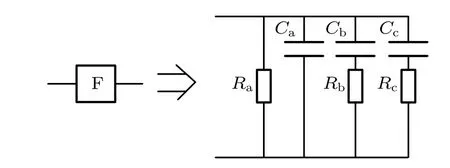
Fig.13. Fractional-order unit circuit with q=0.9.

Fig.14. Phase diagram of x–z plane with q=0.9.

4. Conclusions

In this paper, we studied the nonlinear dynamic characteristics of a new fractional-order multi-scroll chaotic system with sinusoidal nonlinear terms,and also review the history of the fractional-order chaotic system, focusing on the bifurcations, Lyapunov exponents, complexity, and basins of attraction of the 0.99-order multi-scroll chaotic system. We first propose using the Lyapunov exponents to describe the basins of attraction of the chaotic system in the Matlab environment.The result shows that system(1)has the characteristics of hidden attractors,hidden bifurcations,and multi-stability.Finally,the 0.9-order multi-scroll chaotic attractors are implemented by using the simulated circuits. As the multi-scroll chaotic system of the fractional-order has more complex nonlinear behavior, it can describe the physical characteristics of the system more clearly. It is widely applied to such fields as secret communication, image processing, artificial neural network,etc. The hidden attractors and hidden bifurcations are new concepts that have been proposed only in recent years. The hidden attractor chaotic system has more complex nonlinear dynamic behaviors, so it is necessary to carry out more indepth research on this type of system.