基于最小二乘向量机结合双向时序长短期记忆的台区用电特征提取*
2021-03-11程昱舒谢振刚陈安琪
程昱舒,谢振刚,陈安琪
(1.国网山西省电力公司营销服务中心,山西 太原 030002;2.国网山西省电力公司,山西 太原 030021)
随着智能电网、能源互联网和泛在电力物联网建设的发展,风、光、水、核等可再生能源大量、不断地并入电网的各个角落,使电网的调度、控制难度越来越大,因此精细化地掌握用户用电的特征和趋势就显得越来越重要,已经成为电力系统研究的热点问题之一,引起国内外专家学者的广泛重视[1-3]。
泛在电力物联网建设的重要一环就是高级量测系统的形成,并能够采集电力系统发、输、配、用各个环节数据,尤其是智能电表的安装,可以获得配电网用户侧各个时段的用电信息,从而为用电特征的提取提供了重要基础[4-5]。
基于电力系统高级量测体系,目前对于电力系统台区用电特征的研究有如下的代表性成果,如文献[6]基于高级量测体系形成的多元大数据平台,建立了配电网用电行为特征的分析构架;文献[7-9]针对赤峰市、厦门市、湖南省等多用户农村住宅实际年、月生活用电量,分别从年、月、日、小时等尺度分析了农村住宅用电量规律;文献[10-13]基于聚类思路,分别采用K-Mean 方法、云平台计算方式获得用户用电行为特征;文献[14-16]从构架方面,给出了用户画像的不同技术框架下的关键实现技术和应用。
对于电力系统大数据的分析和应用是用户用电特征分析和提取的有力保证,然而目前的研究成果在提取用电特征时,仍以传统方法为主,没有使用人工智能领域的相关新成果。本文以此为切入点,以深度学习理论中的双向时序长短期记忆网络(Bidirectional Long Short-Term Memory,BLSTM)为手段,以最小二乘支持向量机回归模型为前提,综合考虑天气环境信息、人文活动信息、经济社会信息,提出了台区用户用电特征提取方法。
1 台区用电特征提取
用电行为特征提取的核心是获得用户用电的特征,即通过真实的量测数据进行聚类分析:

式中:SSE 表示传统的误差平方和计算方法;k表示该划分中的个体数量;ci表示第i个划分;x表示ci中的个体;mi表示样本均值。
式(1)描述了样本分类过程中的计算准则,然后使用K-Means 聚类算法能够获得具有多个特征的聚类。
在传统K-Means 聚类算法的基础上,进一步采用最大熵原理来进行特征精细化过滤,随机变量x的计算熵为:

式中:Ω为随机变量x取值集合;p(x)为随机变量x的概率。
在传统K-Means 聚类分类d中,所有用户特性的熵为:

式中:Nd表示分类总数;Mi表示第i个分类的总样本。
获得用户特性熵后,可以计算特征ti与用户类别之间的最大相关信息熵D(s,d):
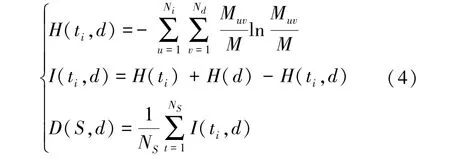
式中:Muv表示特征ti在分类v中的总样本;I(ti,d)表示S中的特征ti与分类d之间的信息相关度;S表示经过筛选后的最优特征集;NS表示该集合中的特征数量。
获得式(4)后可以辨别特征与分类之间的信息相关度,进而定义相关系数ρ(ti,tj):

式中:cov(ti,tj)表示特征ti和tj的协方差;和分别为特征ti和tj的标准差。
相关系数表示的是特征之间的关系,还要从最优的角度进行去除分类内的冗余,因此需要设置冗余指标:

结合式(4)~式(6),可以获得最优特征分类:

利用机器学习方法求解式(7)后即可得到用户用电特征的最优分类,从而形成用户用电特征提取。
要想求解式(7),可以采用机器学习中的相关方法,在电力系统量测大数据环境下,基于人工智能的方式可以获得精度较高的特征解。
为了获得精度高的特征解,下面首先给出最小二乘支持向量机的回归模型,然后以此为基本解,采用深度学习中的双向时序长短期记忆网络方法对基本集进行学习,从而获得精度更高的解。
2 最小二乘支持向量机回归模型
根据第1 部分的内容可知,用户用电特征提取的本质就是对用户用电进行分类,即依据电力系统量测的历史大数据,对其中具有相似特征的进行分类,形成若干类。每一类具有相似的用电特征。而分类的方法可以使用模式识别中的支持相量机(Support Vector Machine,SVM)方法。传统SVM 具有收敛速度慢、容易陷入局部极值的问题,为了克服这些问题,本文采用最小二乘支持向量机回归模型。
最小二乘支持向量机(Least Square Support Vector Machine,LSSVM) 是对传统支持向量机(Support Vector Machine,SVM)的改进,是一种遵循结构风险最小化(Structural Risk Minimization,SRM)原则的核函数学习机器,其算法是最小二乘法,其原理是结构风险最小化,克服了传统经验风险最小准则泛化能力差、求解速度低的缺陷。已经在电力系统负荷预测、风电预测等方面得到广泛应用[17-18]。
设存在电力系统潮流量测大数据,选择时间窗为n的时间断面量测,使用这n个时间断面量测历史数据作为训练样本,设为训练样本对(xi,yi)(i=1,2,…,n),其中xi表示输入样本,yi表示输出样本。
根据SVM 原理,可以将该样本对在非线性映射函数φ(x)的作用下,映射到高维特征空间中:
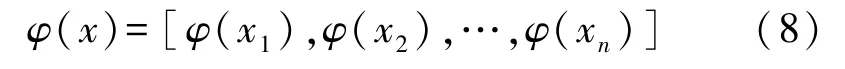
在式(8)所示的特征空间中,建立如式(9)的线性回归函数:

式中:w表示权相量,wT为其转置;b为偏移量。
根据SRM 原理求解式(9),等效为如下的计算:

式中:γ为一系数,当其为无穷大时,所得到的解为最小二乘优化解;Remp为SRM 函数,可以表示为Remp表示第i个时间断面中训练过程中的误差。
为了求出式(9)中的参数w和b,在式(10)的基础上,可以建立如下的优化模型:

一般来说,式(11)可以通过建立拉格朗日函数来求解:

式中:λ=[λ1λ2…λn]T表示拉格朗日乘子。
依据拉格朗日乘子法中的最佳解条件,即KKT(Karush Kuhn Tucker)条件,可以求解式(13)得到:

展开式(13)可得:

求解式(14)中的w和εi,可以转换为如下的线性方程组的形式:
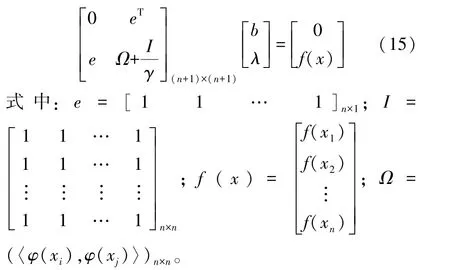
在计算式(15)的方程过程中,需要给定核函数才能进行计算。设满足Mercer 定理的核函数为K(xi,xj)=[φ(xi),φ(xj)],那么求解式(14)就可以等效为求解如下的回归函数:
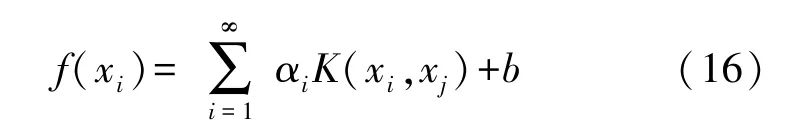
由于径向基函数具有较强的泛化能力,因此在计算式(16)时,通常选择径向基函数作为核函数,即:

式中:σ表示径向基函数的尺度参数。
将式(17)代入方程组(15)中,利用最小二乘法原理就可以得到参数的估计值:

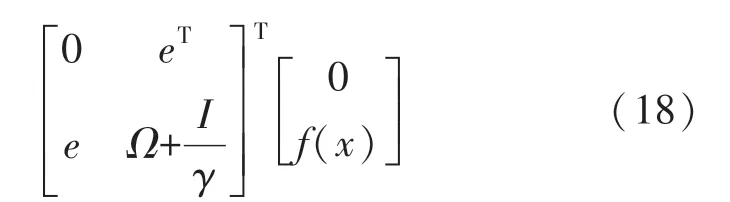
将式(18)估计结果代入式(14)中,可得:

根据式(8)~式(19)的计算,可以获得台区用户用电特征分类,该分类是通过对台区历史量测的大数据进行统计分析获得的,但是还存在一定的误差。
为了获得精确度更高的特征分类,将误差以及式(8)~式(19)获得的解进一步采用双向时序长短期记忆网络的方式进行学习,从而获得精度更高的特征分类。
3 双向时序长短期记忆网络用户用电特征提取
3.1 基本原理
双向长短时记忆网络(Bidirectional Long Short-Term Memory,BLSTM)是由前向、后向两个LSTM 构成,其基本单元如图1 所示,包含输入层、前向LSTM、后 向 LSTM、输出层,具体计算步骤如下[19-20]。
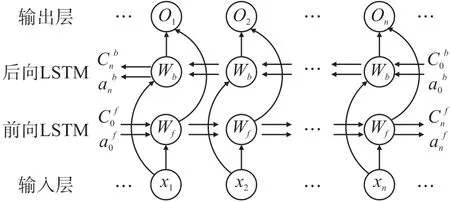
图1 BLSTM 结构图
第一步,中间处理单元的计算:
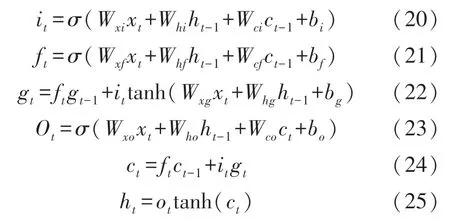
其中,式(20)是对输入层的计算;式(21)对遗忘层的计算;式(21)是对中间层的计算;式(22)是对输出门的计算;式(23)是对记忆融合阶段的计算;式(24)是最后的输出计算。Wxi,Whi,Wci,Wxf,Whf,Wcf,Wxg,Whg,Wxo和Who,Wco为学习训练的权系数;bi,bf,bg,bo为偏置项。
3.2 用户用电特征提取
为了实现准确的用户用电特征分类和提取,在通过电力系统量测的大数据基础上,通过第2 部分的计算,可以选择N个滚动的时间窗口,每个时间窗口包含n个第2 部分的量测断面,从而可以获得N个第2 部分计算的数据样本,标记为:

式中:Δwt表示第2 部分估计的的误差;同理,Δbt表示第2 部分估计的的误差;Δft(x)表示由Δwt和Δbt获得的分类函数的误差值;Pi表示台区历史负荷值,包含了N个时间窗口内、每个窗口内的n个值;Wi表示台区天气环境信息;Ai表示人文活动信息;Oi表示经济社会状态。
将式(26)中的数据样本作为BLSTM 的输入数据,同时选择式(20)、式(21)、式(23)中的过滤函数为sigmoid 函数,设置BLSTM 相应的层数和LSTM个数,从而可以进行学习BLSTM 的权系数。
4 算例分析
采用如图2 所示的山西电网某地区实际电网为例,对本文方法予以验证。该地区电网中共包含5台发电机、11 个用电负荷,电网参数如表1 所示,采集负荷13 某天的有功功率,如表2 所示。
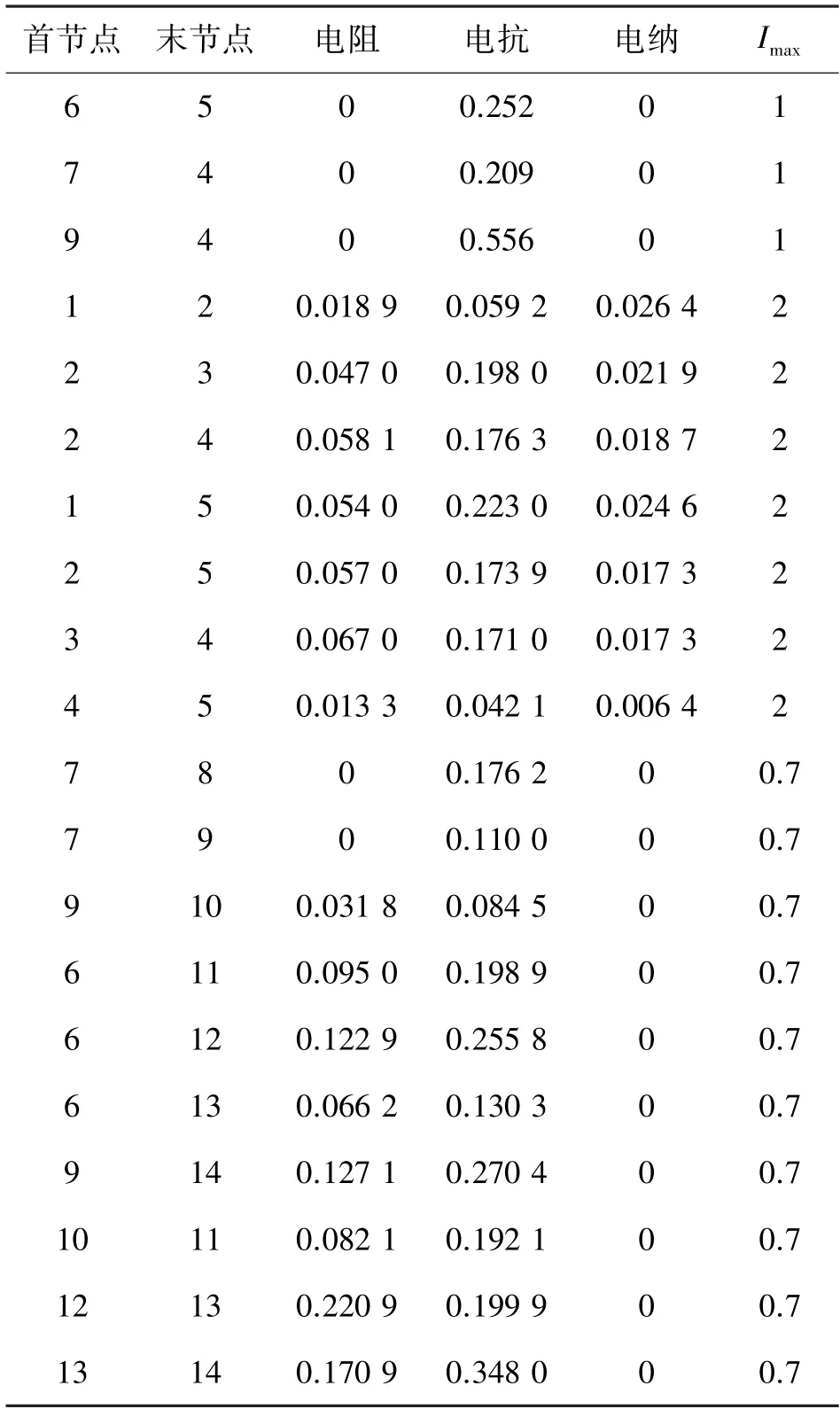
表1 图2 所示电网结构参数(标幺值)

表2 某天24 h 负荷13 的有功功率 单位:MW
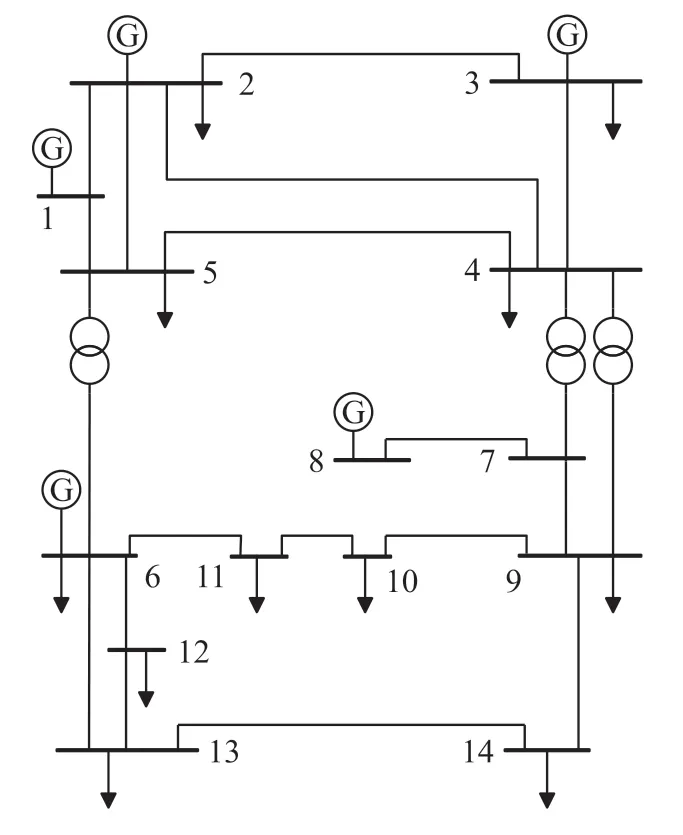
图2 某地区实际电网
采用某年1 月至6 月共6 个月,每个月按照30 d 计算,每天24 h、每小时以15 min 采集系统潮流,共获得17 280 个时间断面的潮流结果,某天潮流结果如表3 所示。

表3 某天24 h 发电机有功潮流结果 单位:MW
在Windows 环境下,采用MATLAB 结合Python对本文算法进行程序设计,文中涉及的数据保存在SQL 数据库中,与Python 和MATLAB 进行配合,编写程序进行计算和分析。
基于上述基本信息和潮流数据,根据本文第1、2、3 部分的方法,进行用电特征分类,可得到如图3所示的分类结果。
由图3 中的4 类分类结果可见,每一类的差别很明显,即可以明确地获得分类结果。从曲线的走势上就可以直观地看到,而每一类中的负荷数据大小和趋势也基本一致。

图3 聚类后4 类用户用电特征曲线
5 结论
针对电力系统精细化管理的要求,准确地获得需求侧用电特征十分必要,因此首先对传统K-Mean典型聚类方法进行改进,获得用户用电特征,并形成学习的历史数据;在此基础上,通过使用最小二乘支持向量机回归模型获得具有较高准确度的用电特征,并获得误差,将其作为后续人工智能学习方法的输入;最后,通过双向时序长短期记忆网络进行深度学习而进行分类。通过实际电网的仿真验证表明了本文所提出的方法能够准确地获得台区用户用电特征。
