水土压力统一计算理论的对比研究

2021-03-11

工程技术研究 2021年2期

广东省冶金建筑设计研究院有限公司，广东广州 510080

当设计支护结构时，需要计算水土压力，其原则是黏性土、黏质粉土水土合算，砂质粉土、砂土和碎石土水土分算[1]。由于土与水作用的微观机理复杂，根据不同种类的土采用水土合算和分算，是长期工程经验总结的结果，其计算结果与工程实际较吻合。但是，完善统一的水土压力计算理论仍然是主要的研究热点之一[2]。

水土压力统一计算理论的研究，均从微观机理的探索开始。通过微观机理研究，部分水土压力统一计算理论被引入水道率计算理论，推导出统一的水土分算和水土合算算法[3-4]；还有使用电镜成像手段，对土中孔隙率进行定量统计，在现有水土压力计算理论中引入土颗粒接触面积影响系数，得出统一的水土分算和合算理论[5]。

采用不同的研究手段得出的水土压力计算理论中，各参数的物理意义也会有区别，但最终影响工程应用的是通过各种理论计算的结果。因此，有必要采用同时满足各计算理论的条件，得出具体的计算结果，对比分析计算结果在工程应用中的可靠性。

1 基于有效应力原理的水土压力计算理论

目前，水土压力统一计算的理论均是从有效应力的理论中推导出来的，即除了部分土层按照水土合算（基于总应力理论）计算土压力，统一采用水土分算计算土压力，从而在理论和形式上均形成统一。因此，在各种理论的对比研究中，可将计算土压力的土层限定在黏性土、黏质粉土的范畴。土压力均采用朗肯土压力，且只考虑孔隙静水压力。

黏性土、黏质粉土等按水土合算，是基于总应力理论，主动土压力如下[6]：

式中：γsat为计算土层饱和重度，kN/m3；z为计算点土层深度，m；Ka、Kp为主、被动土压力系数；c为黏聚力，kPa；φ为内摩擦角，°。

1.1 引入水道率的水土压力统一计算理论

引入水道率的水土压力计算公式，是根据有效应力原理，引入水道率参数ξ。主动土压力如下：

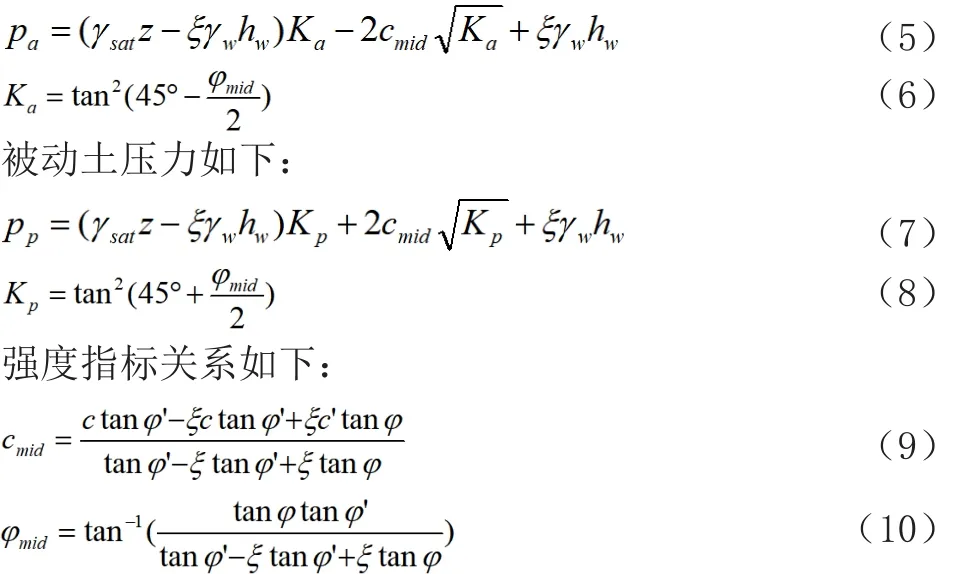
式中：γsat为计算土层饱和重度，kN/m3；γw为水重度，kN/m3；z为计算点土层深度，m；hw为计算点地下水深度，m，Ka、Kp为主、被动土压力系数；c为黏聚力，kPa；φ为内摩擦角，°；c’为有效应力黏聚力，kPa；φ’为有效应力内摩擦角，°；cmid为引入水道率有效应力黏聚力，kPa；φmid为引入水道率有效应力内摩擦角，°。

1.2 考虑土颗粒接触面积的水土压力统一计算理论

利用电镜图像对土颗粒接触面积和孔隙面积进行统计分析，引入平均孔隙面积率。主动土压力如下：

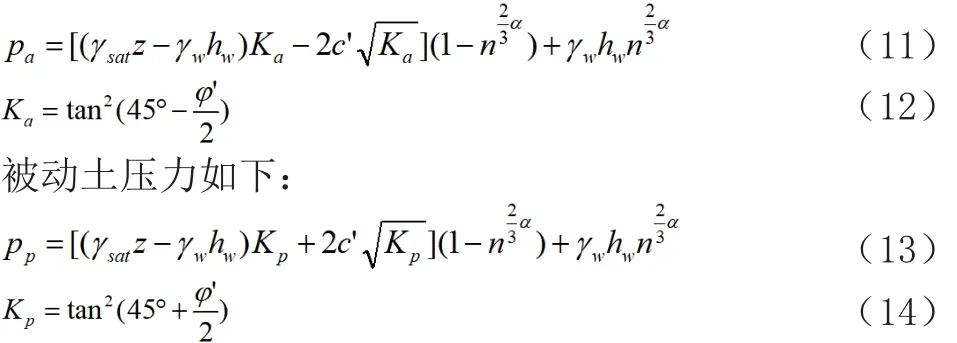
式中：γsat为计算土层饱和重度，kN/m3；γw为水重度，kN/m3；z为计算点土层深度，m；hw为计算点地下水深度，m；Ka、Ka为主、被动土压力系数；c’为有效应力黏聚力，kPa；φ’为有效应力内摩擦角，°；n为土体的孔隙率；α为待定参数，与软土成分含量和区域有关。

2 水土压力统一计算理论的对比研究

黏性土、黏质粉土等采用水土合算方法计算土压力，其结果通过工程实践证明具有很强的可靠性，亦是规范的推荐使用方法。因此，在相同条件下，用水土合算的结果，与水土压力统一计算理论的计算结果对比，可以确定新理论的实用性和可靠性。

计算选用粉质黏土的土层参数，如表1所示。

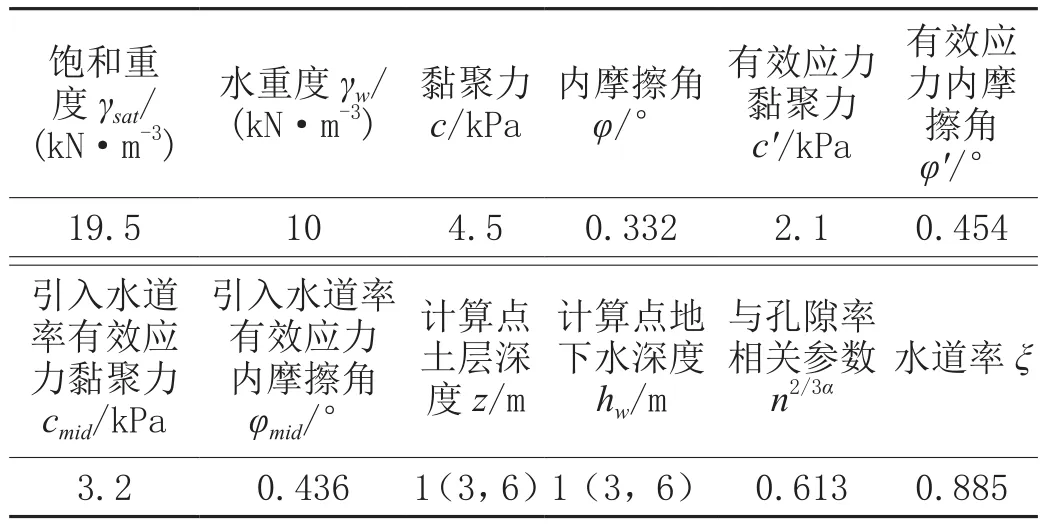
表1 土层参数表

根据土层参数，分别计算主动和被动土压力，如表2、图1、图2所示。

表2 主动土压力和被动土压力计算结果

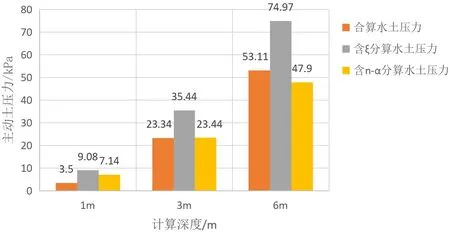
图1 主动土压力结果对比

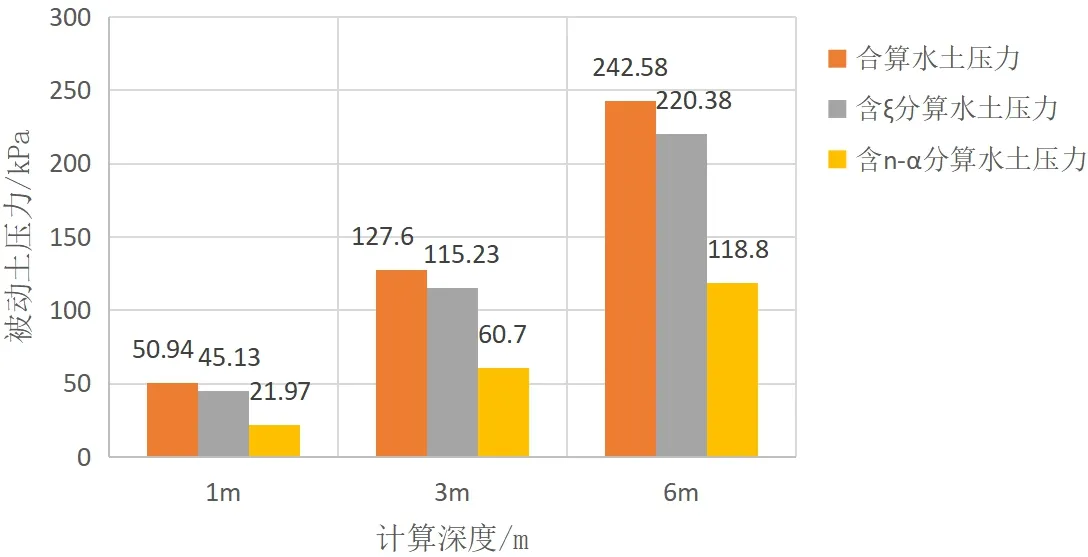
图2 被动土压力结果对比

由表2和图1、图2可知，同一土层单位深度的水土压力，引入水道率ξ的水土压力统一计算方法与传统的水土合算方法计算结果接近。其中，引入ξ的水土压力统一计算方法的主动土压力结果比水土合算结果大5.58kPa，结果差异变化率为159.4%，变化率很大；而比被动土压力结果小5.81kPa，结果差异变化率为11.4%，变化率较小。当取z=hw=3m和z=hw=6m时，主动土压力计算结果差异变化率分别为51.8%和41.2%，被动土压力计算结果差异变化率分别为9.7%和9.2%，即随着计算深度增加，主动土、被动土压力计算结果差异变化率均在减小，但减小的幅度逐渐降低。因此，引入ξ的水土压力统一计算方法的主动土压力结果是偏保守的，而被动土压力结果差别较小，如果采用此算法，经过适当修正，可以满足工程要求。

考虑土颗粒接触面积的水土压力统一计算方法，其主动土压力计算结果与水土合算结果相比先偏大，随深度增加又偏小，结果具有不稳定性特点；而被动土压力结果仅为水土合算结果的0.5倍，偏向不安全。出现这种结果的主要原因是该理论通过分析微观电镜图像并结合统计学原理得到，与复杂的土体构造相比，仍然缺乏普遍性，仍然需要大量样本进一步深入研究。