钢底板-波形钢腹板钢-混组合箱梁剪力滞后效应分析
2021-03-11朱世栋王金凤
刘 星,朱世栋,王 巍,王金凤,李 瑜
1.甘肃彭大高速公路项目管理有限公司,甘肃 平凉 744000
2.甘肃顺达路桥建设有限公司,甘肃 兰州 730000
3.甘肃路桥建设集团有限公司,甘肃 兰州 730000
波形钢腹板钢-混组合箱梁因其具有上部结构自重较轻、箱梁各部受力较为明确、材料利用率高、施工较为便捷的特点,在桥梁工程领域迅速得到应用[1-2]。现有的此类组合结构箱梁主要由波形钢腹板和顶、底板混凝土结构构成[3-6],但随着此类结构在工程领域中的不断应用和探索,新型波形钢腹板钢-混组合箱梁逐渐运用于实际工程中。这种结构优化不仅可以继续有效减轻上部结构的自重,提高桥梁跨越能力,还可以充分利用钢材抗拉强度高的材料特性,减少正弯矩区底板混凝土受拉开裂的现象[7]。为更加方便、准确地得出此类新型结构的剪力滞后分布规律,文章基于附加挠度法对钢底板-波形钢腹板钢-混组合箱梁剪力滞后效应进行分析与研究。
文章以银川至昆明国家高速公路(G85)彭阳(甘宁界)至平凉至大桥村(甘陕界)段建设项目泾河特大桥钢底板-波形钢腹板钢-混组合箱梁桥为例,基于能量变分法,以余弦函数为剪力滞后翘曲位移函数,采用附加挠度作为广义位移来描述钢底板-波形钢腹板钢-混组合箱梁剪力滞后变形状态,引入轴力自平衡条件与弯矩自平衡条件,推导出集中荷载和均布荷载两种典型荷载工况作用下钢底板-波形钢腹板钢-混组合箱梁剪力滞后计算公式,并与ANSYS有限元模型进行对比,验证理论计算方法的正确性,进一步揭示这种新型钢底板-波形钢腹板钢-混组合箱梁的剪力滞后分布状态。
1 钢底板-波形钢腹板钢-混组合箱梁剪力滞后效应分析
1.1 基本假定
以保证足够的计算精度为前提,引入“平截面假定”,同时为方便计算,基于等效刚度法(即ASES=ACEC),将钢底板换算成混凝土底板,得到新的抗弯结构(如图1所示),并对其进行计算分析。由于波形钢腹板的褶皱效应,其轴向的弹性模量很小,因此对轴力和弯矩的抵抗作用可忽略不计,即在采用能量变分法求解时可不计入波形钢腹板的弯曲应变能。

图1 换算后的钢底板-波形钢腹板钢-混组合箱梁抗弯结构
1.2 附加挠度对剪力滞后变形状态的描述
当有任意竖向荷载P(z)作用于钢底板-波形钢腹板钢-混组合箱梁并使梁体竖向挠曲变形时,与初等梁理论下的截面变形不同,其截面变形还应包括由剪力滞后效应引起的翘曲变形,如图2所示。
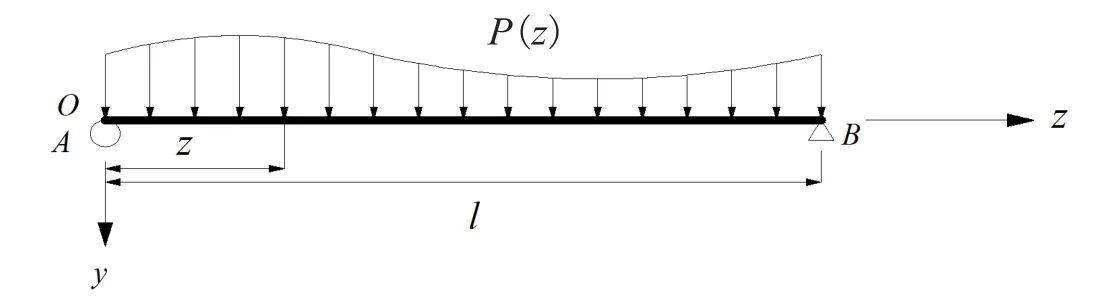
图2 坐标轴与荷载作用示意图
文章以剪力滞后效应影响下钢底板-波形钢腹板钢-混组合箱梁竖向抗弯刚度减小、竖向挠度增大这一现象为基础,以增大的附加挠度作为描述剪力滞后变形的广义位移,计算横截面上任意一点的纵向位移u(x,y,z):

式中:η为引入的弯矩自平衡修正系数;f(z)为剪力滞后效应引起的附加挠度;w(z)为初等梁理论引起的挠度;ωζ(x,y)为剪力滞后翘曲函数;ω(x,y)为相应于附加挠曲转角的广义位移函数,即。
基于胡克定律,可得组合箱梁任意截面一点处正应力的表达式如下:

式中:-Eyw"(z)为基于初等梁理论的正应力表达式;-Eω(x,y)f"(z)为基于剪力滞后效应的翘曲应力表达式。可得:

在竖向荷载作用下组合箱梁任一截面上翘曲应力应满足相应自平衡条件,由此可得:

由式(2)可知,钢底板-波形钢腹板钢-混组合箱梁任意点处的总正应力为剪力滞后效应引起的翘曲正应力与初等梁理论相应的正应力之和,即:

1.3 控制微分方程与初参数解
文章将钢底板-波形钢腹板钢-混组合箱梁的剪力滞后变形形态与初等梁变形状态分离开来研究,受如图1所示的任意竖向荷载P(z)作用的钢底板-波形钢腹板钢-混组合箱梁,其总势能的一阶变分如下:


式中:A、B、C、D为钢底板-波形钢腹板钢-混组合箱梁两段相应边界条件对应的常数。
对于跨内受任一集中荷载P的钢底板-波形钢腹板钢-混组合箱梁(如图3所示),可得相应的附加挠度与广义力矩的计算式如下:

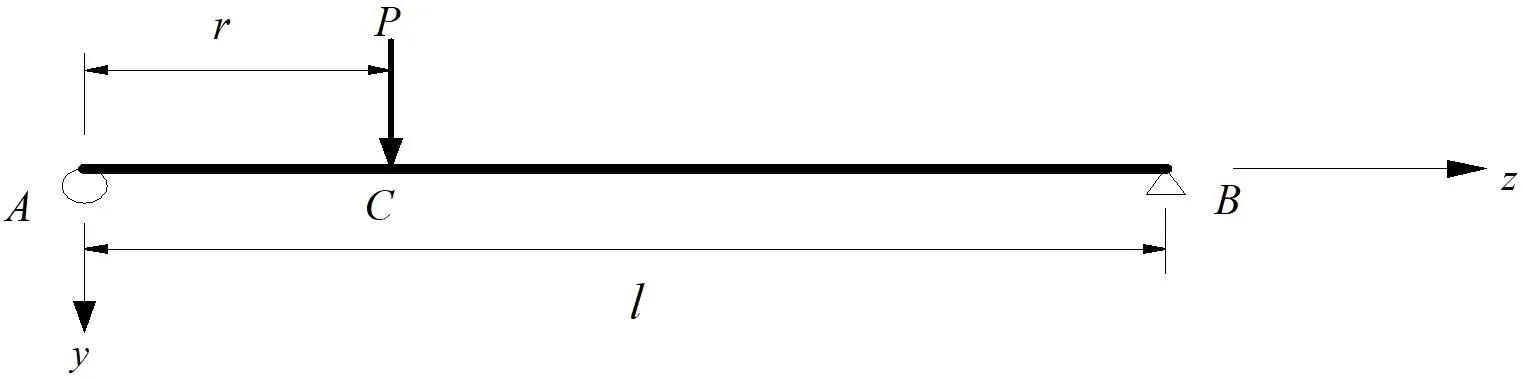
图3 简支梁任一截面受竖向集中荷载P作用
对于跨内受任一满跨均布荷载q的钢底板-波形钢腹板钢-混组合箱梁(如图4所示),可得梁的附加挠度与广义力矩的计算式如下:


图4 简支梁任一截面受竖向均布荷载q作用
1.4 截面几何特性计算
文章选取余弦函数为钢底板-波形钢腹板组合箱梁翘曲位移函数,如图5所示。由此可得如下形式的翘曲位移函数:

图5 梯形横截面箱梁

式中:α为悬臂板影响的修正系数,即α=(b3/b1)2;β为底板影响的修正系数,即β=(b2/b1)2(yx/ys);d为轴力自平衡条件引起的附加轴向位移,d需满足:

由式(25)与式(26)可得d的表达式如下:
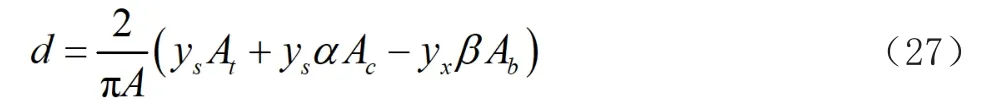
式中:A为组合箱梁横截面面积之和;At为组合箱梁顶板面积;Ac为组合箱梁悬臂板面积;Ab为组合箱梁底板面积。
由剪力滞后翘曲位移函数可推导出其他截面几何特性表达式:

2 算例分析
2.1 有限元模型建立
此小节以银川至昆明国家高速公路(G85)彭阳(甘宁界)至平凉至大桥村(甘陕界)段建设项目泾河特大桥钢底板-波形钢腹板钢-混组合小箱梁为算例,对理论方法进行验证。该桥全长50m,计算跨径48.92m,横截面尺寸及横截面计算点布置如图6所示。

图6 钢底板-波形钢腹板钢-混组合箱梁横截面尺寸(单位:mm)
相应的顶板、悬臂板采用C50微膨胀混凝土,钢底板采用Q370qD钢材,波形钢腹板采用Q345qD钢材。各种材料的主要材料特性值如表1所示。

表1 各种材料的主要材料特性值
计算时,对钢底板-波形钢腹板钢-混组合箱梁跨中施加两种的荷载,如图7、图8所示。

图7 钢底板-波形钢腹板钢-混组合箱梁受集中荷载作用示意图
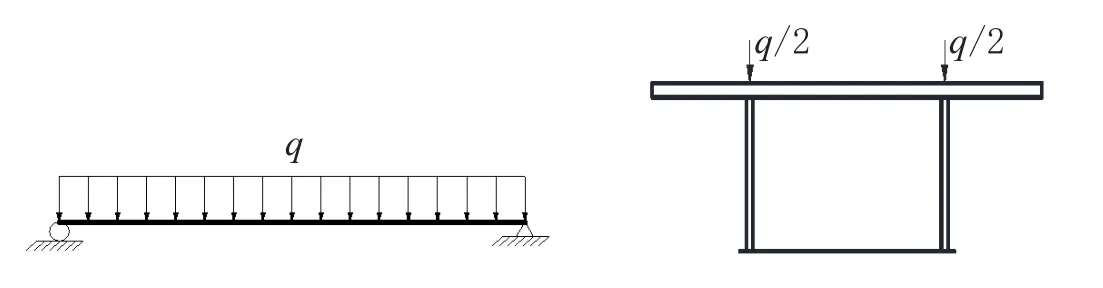
图8 钢底板-波形钢腹板钢-混组合箱梁受均布荷载作用示意图
在建模过程中,采用Solid 45单元来模拟顶板及悬臂板混凝土结构,采用Shell 63单元来模拟波形钢腹板及钢底板结构,各板件结构采用共节点方式进行连接,从而使其协调一致工作,有限元模型如图9所示。

图9 钢底板-波形钢腹板钢-混组合箱梁ANSYS有限元模型
2.2 计算结果对比分析
文章以跨中截面作为计算截面来分析钢底板-波形钢腹板钢-混组合箱梁简支状态下的剪力滞后效应的横向分布,分析时施加如图7、图8所示的集中荷载及均布荷载,得出相应的理论计算结果和有限元模拟计算值,如表2、表3所示。

表2 钢底板-波形钢腹板钢-混组合简支箱梁集中荷载作用下跨中计算截面剪力滞后系数对比

表3 钢底板-波形钢腹板钢-混组合简支箱梁均布荷载作用下跨中计算截面剪力滞后系数对比
由表2、表3可知,受相应跨中集中荷载和满跨均布荷载作用时,运用附加挠度法所得的简支钢底板-波形钢腹板钢-混组合箱梁跨中截面各个计算点的剪力滞后系数与ANSYS有限元模型所得的计算结果较为吻合,最大误差绝对值仅为8.23%。同时,由计算结果可以很明显地看出,剪力滞后系数横向分布规律是由顶板中心和悬臂板端部的负剪力滞后现象向波形钢腹板与顶板、悬臂板相交处逐步过渡到正剪力滞后现象,并且钢底板与混凝土顶板的剪力滞后系数分布规律相同,这证明了文章所述方法的正确性。
3 结束语
文章结合钢底板-波形钢腹板钢-混组合箱梁的结构特点,利用附加挠度法对银川至昆明国家高速公路(G85)彭阳(甘宁界)至平凉至大桥村(甘陕界)段建设项目泾河特大桥钢底板-波形钢腹板钢-混组合箱梁剪力滞后效应进行研究,得到以下结论:
(1)以等效刚度法为基础,将钢底板换算成混凝土底板,得到新的钢底板-波形钢腹板钢-混组合箱梁抗弯结构模型,利用考虑自平衡条件后的附加挠度法在两种荷载工况下计算出的钢底板-波形钢腹板钢-混组合箱梁各点的剪力滞后系数与ANSYS有限元模型计算结果吻合良好,证明了文章所述方法的正确性。并且由计算结果可知钢底板-波形钢腹板钢-混组合箱梁存在明显的剪力滞后现象,在此类桥梁设计及施工中为保证结构的安全与稳定,应充分考虑该现象对桥梁结构的影响。
(2)由计算结果可以看出,在两种荷载工况下,顶板、悬臂板及底板随着横坐标发生变化,与此同时钢底板-波形钢腹板钢-混组合箱梁横截面上会出现正、负剪力滞后效应变化现象,由此揭示了剪力滞后效应在钢底板-波形钢腹板钢-混组合箱梁上的横向分布情况。
