基于Kubelka-Munk双常数理论的色纺纱配色模型
2021-03-11杨瑞华
王 卓 杨瑞华 潘 博 王 鑫
(江南大学,江苏无锡,214122)
随着现代文明不断进步,绿色环保理念已经逐渐融入各行各业,环境与经济之间的矛盾,也随之成为了各个领域亟待解决的问题。化纤原液着色技术是一种环保型的再生纤维生产方法。在粘胶纺丝原液中加入着色剂,再经纺丝得到的有色粘胶纤维,具有生产加工流程短、生产方式节能减排、产品色牢度强和色泽均匀的优点[1]。据统计,相较于常规本色纤维,采用原液着色可节约水耗89%、降低能耗63%、减少CO2排放量62%[2]。色纺纱通过单色或者多色纤维的混纺,生产有色纱线,可减少织物染色污染,所成织物色彩立体感强、颜色丰富,并可开发多种新型品种。数码转杯纺是实现混纺比可控的色纺纱柔性生产技术,通过不同比例三基色(红黄蓝)纤维的混纺,可生产各种彩色纱线。该生产方法既具有现代转杯纺技术高速高效、原料适用性强、纺纱流程短的特点,也具有数码纺纱智能化、个性化、多样化的优点[3]。色纺纱产品的配色是其生产中关键的技术问题。混色纺纱的配色不同于织物或纤维染色获得的均一颜色效果,具有复杂的物理过程,既不完全是光线的加法混合,也不完全是颜料的减法混合[4],混色效果更具有层次感。因此色纺纱的颜色需要通过模拟配色、试纺试验及织样试验才能够最终确定[5],过程繁杂。研究者分别提出了Stearns-Noechel、Kubelka-Munk 双常数、Friele 模型,以提高色纺纱的配色智能化和灵便化[6-7]。然而现有的配色系统受生产方法、纤维种类及混纺比例的影响,不能完全适用于新型混配色纱线。
本研究基于Kubelka-Munk(以下简称K-M)双常数理论进行了大量试验,以研究数码转杯纺原液着色粘胶混色产品的智能配色系统,希望可以加快不同种类色纺纱智能化生产进程,完善现有色纺纱配色系统。
1 试验
1.1 原料与仪器
试验原料:博拉经纬纤维有限公司生产的棉型原液着色粘胶纤维,包括红色(Spunshades 9818)、黄色(Spunshades 4274)、蓝色(Spunshades 2925),纤维长度38 mm,纤维细度1.33 dtex。
试验仪器:FA016 型混棉机(江苏金昇实业股份有限公司),A186G 型梳棉机(青岛永佳纺织机械制造有限公司);FA320A 型并条机(南通宝成精密设备有限公司);THC2015 型粗纱机(同和纺织机械制造有限公司);TR-1 型数码转杯纺纱机(江南大学);HC21K 型小型针织圆纬机(无锡市天翔针织机械有限公司);Datacolor650 型分光光度计(Datacolor LTD)。
1.2 样品制备
设计合适的纺纱工艺参数,将红、黄、蓝三种颜色的粘胶短纤维依次通过混棉、梳棉、并条和粗纱,纺制成定量为5.46 g/10 m 的粗纱,再利用TR-1 型数码转杯纺纱机,以10%为质量比例梯度纺制成捻向为Z 向、捻度为72 捻/10 cm、线密度为44.85 tex 的混色纱线。此后,利用HC21K型小型针织圆纬机,将制成的混色纱线织成线圈密度为112 个/cm2的针织纬平纹织物。将红、黄、蓝三基色以10%质量比例为梯度制备混色纱,可得到单组分混色纱3 种,双组分混色纱27 种,三组分混色纱36 种,共66 个样品。混色纱样品编号及纤维质量比例见表1。
1.3 织物颜色测试
将织成的66 个针织样品折叠成不透光状态,利用Datacolor650 型分光光度计进行织物颜色测试,试验条件∶D65 标准光源、10°视场、30 mm 测试孔径。其中光源波长取值范围为360 nm~700 nm,取值间隔为10 nm。为减少试验误差,可以多次测量针织样布不同部位的反射率值和色度值,本试验重复测量次数为10 次。
2 K-M 双常数理论
K-M 理 论 是Kubelka 和Munk 于1931 年提出的理论,这一理论的使用需满足以下4 个条件[8]∶一是物体厚度足够且不透光;二是光线在物体中呈完全扩散状态;三是物体界面上折射率无变化;四是光线在物体中运动方向只有两种(一种向上,一种向下),且与界面呈垂直关系。在K-M 理论中,物体反射率R与吸收系数K和散射系数S关系见式(1)。

K-M 理论分为单常数理论和双常数理论,由于单常数理论更适用于纺织品染料染色配色,故研究者在此基础上提出了更适用于色纺纱有色纤维混色的双常数理论[9-10]。根据K、S的加和特性,简化后可以得到双常数理论见式(2)。

式中∶K1、K2、…、Ki和S1、S2、…、Si分别为混色纱线中各单色纤维的吸收系数和散射系数,c1、c2、…、ci为混色纱线各单色纤维质量比,且c1+c2+…+ci=1。
3 构建配色模型
3.1 最小二乘法
最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小[11]。在本研究中,将利用最小二乘法求解红、黄、蓝三基色纤维的吸收系数K和散射系数S[12]。
将式(2)进行移项可得式(3)。
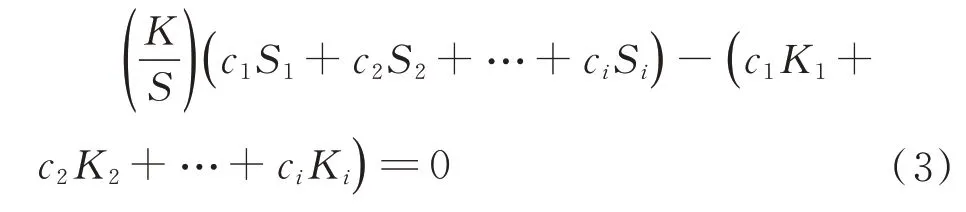
假设共有m个混色织物样品,根据最小二乘法的原理,且目前已知混色织物的实际K/S值[通过实际测得反射率值代入式(1)计算得到]和混色织物中各单色纤维比例,故可将线性方程中的系数常量做以下定义。
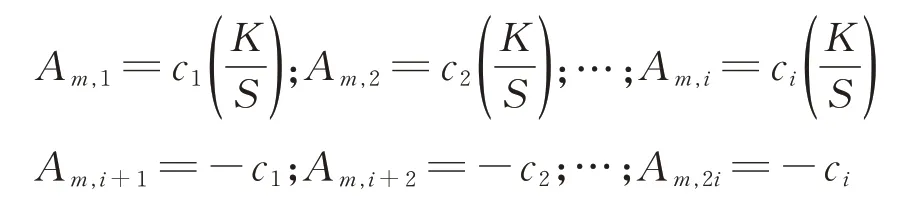
由此可得到矩阵,见式(4)、(5)、(6)所示。
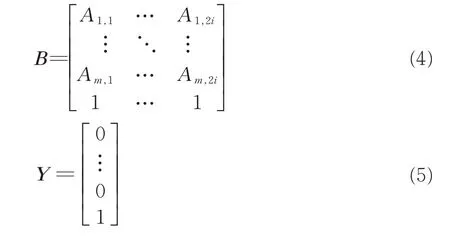

由此,m个混色织物的线性方程组可用矩阵表示,见式(7)。

通过最小二乘法进行矩阵运算,可得到线性方程的解,见式(8)。

利用式(8)即可求出某一波长下红、黄、蓝三单色织物的K值、S值。
3.2 相对值法
相对值法最初由Burlone[13]提出,用于计算有色锦纶的K值、S值。对于两种纤维混色时,则存在以下关系,见式(9)、式(10)、式(11)。
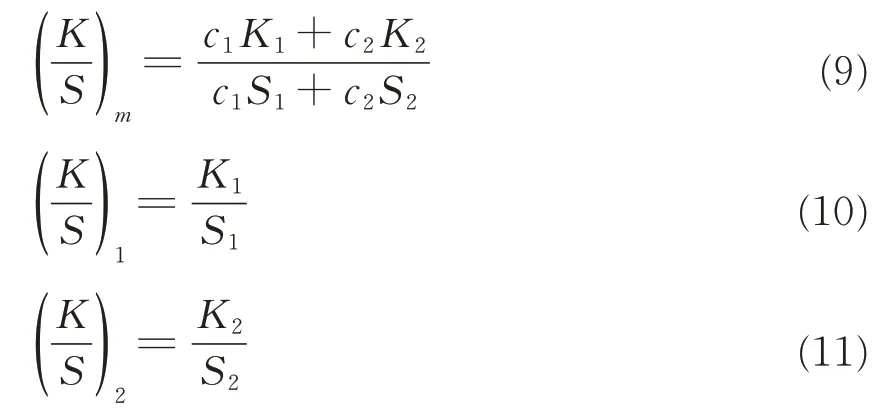
式中,(K/S)m为编号为m的混色织物的实测K/S值;c1、c2为混色织物中两种单色纤维的比例,且和为1;K1、K2分别为两种单色纤维的吸收系数;S1、S2分别为两种单色纤维的散射系数;(K S)1、(K S)2分别为两种单色纤维实际测得的K/S值。
我们假设其中一种纤维的散射系数S2=1,则联立方程(9)、(10)、(11),则可得出。

由此可得到另一种纤维的相对K值、S值,但是通过相对值法求得的单色纤维K值、S值只是相对的,并非单色纤维本身固有的K值和S值,不能够直观得表征有色纤维的颜色。
3.3 色差计算
通过最小二乘法或相对值法,可以得到红、黄、蓝三种单色织物在特定波长下的K值和S值,进而求出一定混色比例时混纺织物的预测K/S值,将式(1)转换为式(15)并代入预测K/S值则可以计算出相应的反射率R值,再通过三刺激值转换即可得到相应织物的预测色度值。将混色织物的预测色度值与实际色度值代入纺织品常用色差公式CMC(l∶c),色差越小,说明预测反射率与实际反射率越接近,预测效果越好,预测精度越高。一般取l∶c=2∶1。色差计算原理见式(16)[14]。
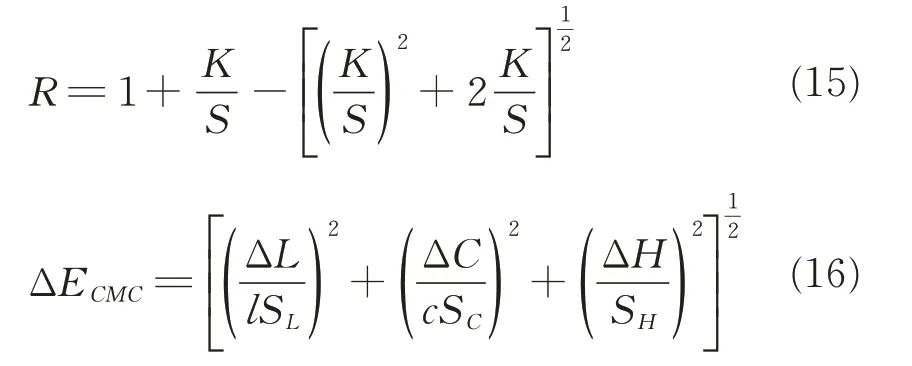
式中:ΔECMC为色差值,ΔL、ΔC、ΔH分别为明度差、饱和 度差、色 相差;SL、SC、SH分 别为ΔL、ΔC、ΔH的加权系数;l=2,c=1。
3.4 结果分析
在最小二乘法中,利用编号为4~30 的双组分混色针织样品进行分析试验。为了保证试验数据的准确性,增大样本量,将27 种双组分纱线视为三基色纤维混和,样品中所缺少单色纤维的质量比例设为0,再利用试验所测数据代入式(8)得到三种单色纤维在一定波长下的K值、S值,每种单色纤维可得到35 组数据。利用最小二乘法计算所得单色纤维K值、S值如图1 所示。
在相对值法中,将蓝色纤维的散射系数设为1,则可利用编号为4~12 和13~21 的针织混色样品所测已知数据代入式(12)、式(13)、式(14)分别求出黄色纤维和红色纤维在不同比例下的K值、S值,再取平均值作为三基色纤维的K值、S值。利用相对值法计算所得单色纤维K值、S值如图2 所示。
分别利用最小二乘法和相对值法所得K值、S值预测编号4~30 混色样品的色度值,再利用色差式(16)计算预测值与实际值之间的色差,结果见表2 和表3。
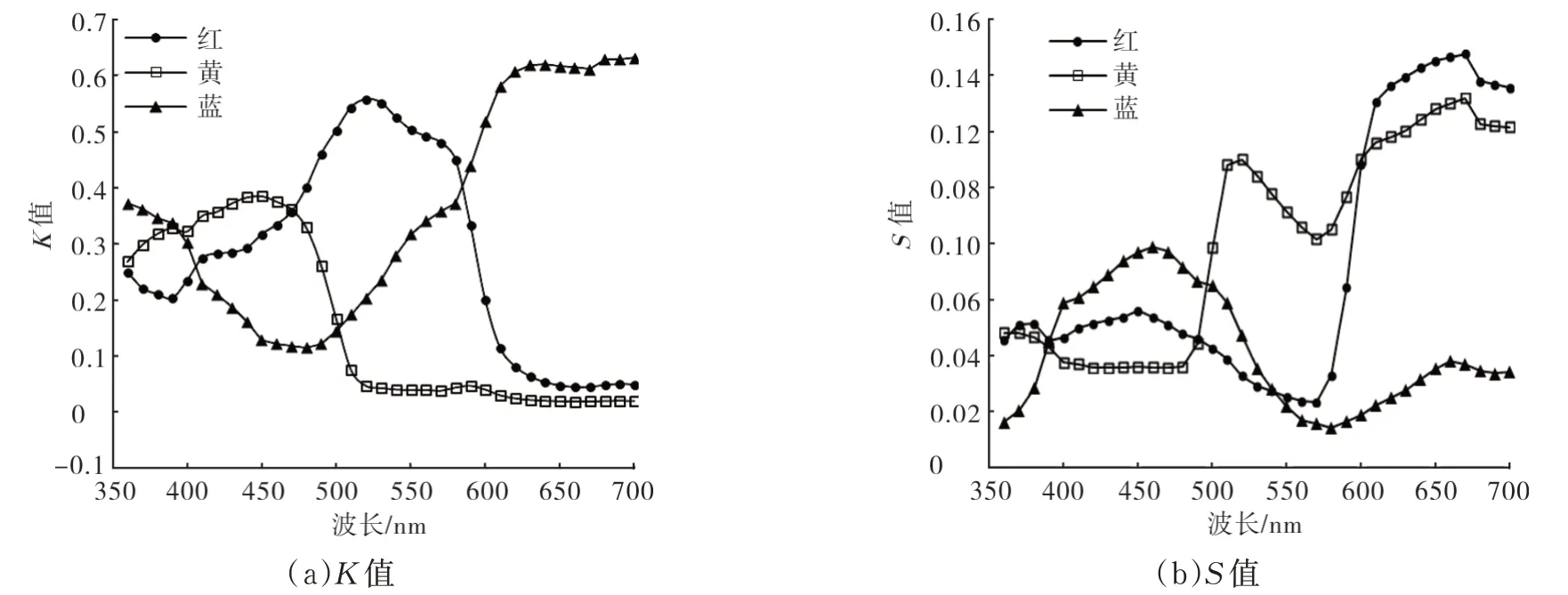
图1 最小二乘法所得单色纤维的K 值和S 值
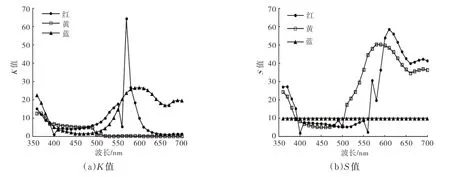
图2 相对值法所得有色纤维的K 值和S 值
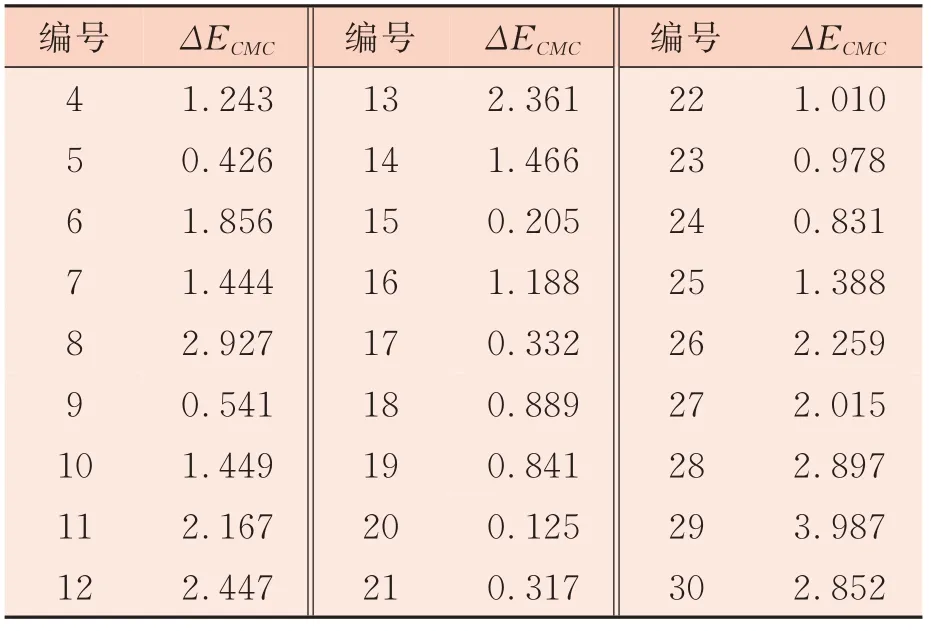
表2 混色样品色差(最小二乘法)
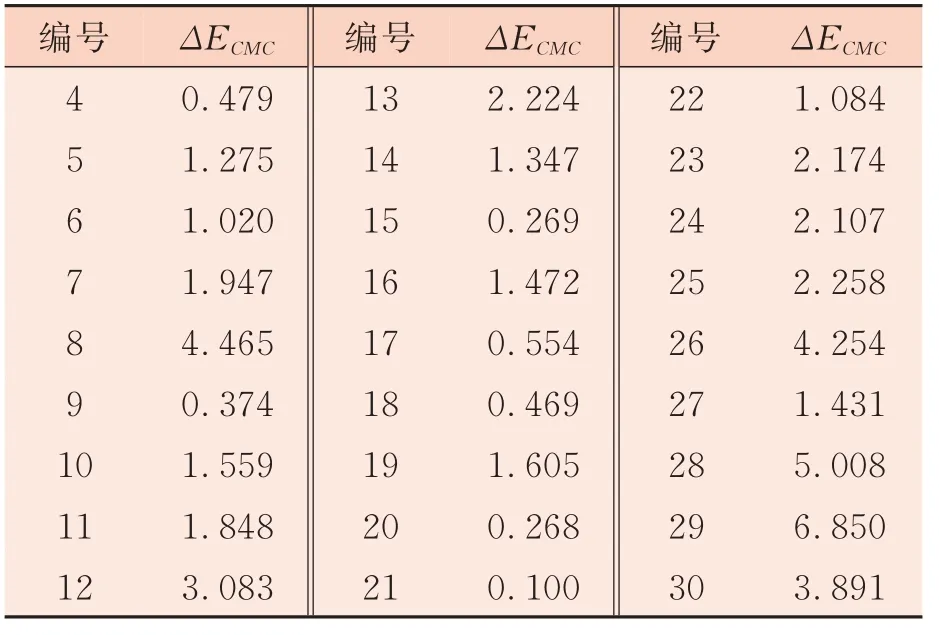
表3 混色样品色差(相对值法)
从表2 中可以看出,最小二乘法算得色差平均值为1.498,相对值法算得色差平均值为1.978。分别统计两种方法的27 个样品色差分布情况,如图3 所示。从图3 中可以看出,两种方法的色差值均主要分布在0~3 之间,而相对值法在大于3 的色差范围内样品数量较多。综合比较,最小二乘法对针织混色样品来说,预测精度较高。

图3 最小二乘法与相对值法的色差分布情况
深入分析可知,无论是哪一种方法,编号8、12、26、28、29、30 的色差值都较大,这可能是试验误差导致的,同时这6 个混色样品中黄色纤维占比都较高,则也可能是K-M 理论在预测黄色纤维的反射率值时适应性较弱导致的。现分析编号1~3 的单色样品的实际R值,与利用K-M 理论得出的单色纤维预测R值进行比较,结果如图4所示。

图4 单色织物实际反射率值与预测反射率值对比
分析图4 可知,最小二乘法中黄色纤维的实际反射率值与预测反射率值相差较多,而相对值法中几乎无差别,但是,利用最小二乘法进行模拟时6 个突出样品(编号8、12、26、28、29、30)的色差较小,故排除黄色纤维占比较多带来的影响,认为这6 个突出样品色差较大是试验误差导致的。剔除掉这6 个突出样品进行分析,最小二乘法算得平均色差为1.099,相对值法算得平均色差为1.232,仍可得出最小二乘法预测精度更高的结论。为了更加直观比较两种方法,选择利用箱型图对两种方法所得色差值进行分析比较,混色针织样本色差箱型如图5 所示。
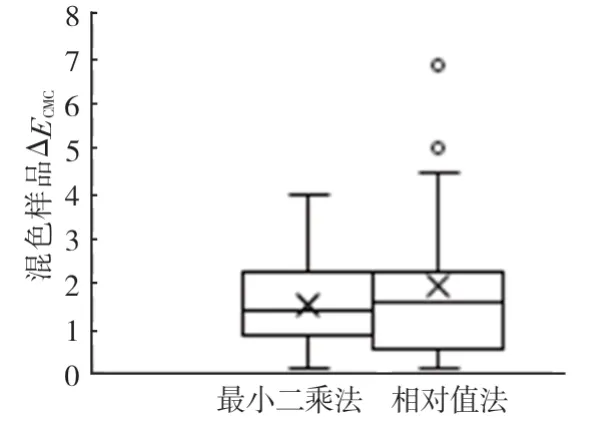
图5 混色针织样本色差箱型
从图5 中可看出,最小二乘法的箱体较小,色差分布较为集中,预测效果更稳定。因此选择最小二乘法所得K值、S值进行K-M 配色模型构建。
4 K-M 双常数理论配色结果
为验证所构建的配色模型的精确度,现对编号31~66 的混色纱线所制成的针织物进行配方比例预测,计算预测比例下预测样本的色度值,并计算其与实际测得色度值的色差。K-M 模型验证结果见表4。同时,引入“比例误差”这一评价指标,用于判断验证结果。比例误差越小,则表示构建的配色模型越精确,比例误差的计算方法见式(17)。

表4 K-M 模型验证

式中:ΔR表示比例误差,xi表示混色样品中第i种有色纤维的实际比例,xi'表示混色样品中第i种有色纤维的预测比例。
由表4 可知,36 个混色样品的比例误差基本都在0.2 以下,平均比例误差为0.097 9,预测比例与实际比例偏差较小;平均色差为0.465,配色结果较好。
混色样品的预测色度值与实际色度值对比图如图6 所示。

图6 混色样品预测颜色与实际颜色对比色卡
图6 为混色样品预测颜色与实际颜色对比色卡,有标记的表示实际颜色,无标记的表示预测颜色。可以看出,预测颜色与实际颜色几乎无肉眼可见的差别,K-M 模型对于数码转杯纺粘胶针织混色织物配色预测的适用性较强。
5 结论
为完善色纺纱智能配色系统,本研究基于KM 双常数理论针对数码转杯纺原液着色粘胶纤维针织混色织物进行了配色模型研究,分别利用最小二乘法和相对值法求得的单色织物吸收系数K值和散射系数S值进行配色预测,并进行比较分析。结果发现,两种方法预测样品的平均色差相差较小,仅相差0.48,然而最小二乘法所预测样品的色差值分布较为集中,离散程度较小,大于3 的色差值较少,故认为最小二乘法预测精度更高,最终选用最小二乘法所得K、S值进行配色模型构建。
在配色模型精确度预测试验中,混色样品比例误差较小,仅为0.097 9,平均色差较小,仅为0.465。此外,从混色样品预测颜色与实际颜色对比图中可以看出,预测颜色与实际颜色几乎无肉眼可见的差别,K-M 模型对于数码转杯纺粘胶针织混色织物配色预测的适用性较强。
