三角函数诱导公式体验式学习法
2021-03-11广西钦州市高新区实验学校李凤东
广西钦州市高新区实验学校 李凤东
三角函数诱导公式的推导涉及较多的知识,显得比较抽象,公式难理解、易遗忘。为了对学生学习和记忆公式有所帮助,通过三角函数诱导公式的体验式学习,解决难学难记的问题。
一、体验一:假设a 为锐角

二、体验二:去“圈圈”和去“-”号(诱导公式一、三的推导)
公式一包括:sin(2kπ+a)=sina,cos(2kπ+a)=cosa,tan(2kπ+a)=tana,其中k∈Z。方法是:直接把2kπ去掉,即把“圈圈”去掉,从而达到“大化小”的目的。注意:去掉2kπ 后,三角函数不变。
例1:化简sin764°=sin(2×360°+44°)=sin44°。
例2:化简cos(-60°)。
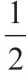
三、体验三:去掉π三角函数不变(诱导公式二、四的推导)
公式二包括:sin(π+a)=-sina,cos(π+a)=-cosa,tan(π+a)=tana;公式四包括:sin(π-a)=sina,cos(π-a)=-cosa,tan(π-a)=-tana。推导方法和步骤如下:
1.假设:a 为锐角;
2.定“三角”:公式二和公式四是关于角(π+a)和(π-a)的三角函数,去掉π 之后,三角函数都是不变的,即:等号左边是正弦,右边还是正弦;等号左边是余弦,右边还是余弦;等号左边是正切,右边还是正切。简记为:去掉π 三角函数不变。
3.定“正负”:去掉π后的结果是正还是负,由角(π-a)和(π+a)对应的“一全二正弦,三切四余弦”来判断。
例3:(1)化简cos(π-20°)。
步骤:1.定“三角”:因为去掉π,所以cos 不用改变,结果仍然是cos;
2.定“正负”:因为角(π-20°)为第二象限角,其余弦值为负,所以等号右边取“-”号,所以cos(π-20°)=-cos20°。
(2)化简tan(π+20°)。
步骤:1.定“三角”:因为去掉π,所以tan 不用改变,结果仍然是tan;
2.定“正负”:因为角(π+20°)为第三象限角,其正切值为正,所以等号右边取“+”号,所以tan(π+20°)=tan20°。

当然,上题(2)的化简,用“如果两个角互余,则其中一个角的正弦等于另一个角的余弦”来化简更直接。
例5:(1)化简sin(-600°)。
步骤:1.去“-”号:在定义域 内y=sin a 为奇函数,sin(-600°)=-sin 600°;
2.去“圈圈”:-sin 600°=-sin(360°+240°)=-sin 240°;3.定“三角”:sin 240°中角度去掉180°,所以sin 不变,仍然是sin;