面向农业园区污染源监测的多无人机路径优化方法研究*

杜心怡，徐 玲，苏莹怡，何羽亭，张 旭，丁 涛

（中国计量大学，浙江 杭州 310018）

我国现有各级农业园区和农业生产基地在促进产业集聚和推动经济发展中贡献重大。但与此同时，园区生产过程中引发的环境问题也日益突出，成为环境污染的集聚区域。政府部门通过加强对农业园区污染源的日常环境监察和巡查，有利于及时评估园区范围内的大气污染状况、监控各污染源排放现状并快速确定超标排放污染源的准确位置，对实现园区大气污染的靶向治理和制定有效的应急处置方案具有重要意义。目前污染源的日常环境监察一般采用固定监测站、无线传感器网络、监测车或手持式监测仪等方式。超标污染源的定位一般通过将其监测位置和污染物信息浓度相综合，得到较粗略的浓度分布图，进而估计出污染源的位置[1]。但由于受地面条件、建筑物和城市道路限制，上述监测手段往往效率不高。同时由于监测点位往往分布不均匀，且事故污染源附近不一定恰好设有监测站或被监测点所包围。虽然可以通过增加监测站数量和观测频率来提高环境监测质量，但仍面临着监测范围有限、成本高昂且机动性差的问题。目前研究结果表明，无人机环境监测平台具有机动、灵活和监测范围广等优势，可以弥补现有固定监测站和监测车的不足，更有利于对大气污染源进行日常环境巡查[2-3]。单架无人机进行园区内大气污染源监测时，由于受无人机自身续航时间限制，一次飞行只能完成部分污染源点位的监测任务，监测任务的执行效率不高[4-5]，也不满足多个污染源在监测时间上尽量保持同步性的要求。因此，采用多架无人机来完成多个污染源的监测十分必要[6-8]。如何根据农业园区污染源监测的特定问题来研究构建目标函数和约束条件，并采用合适的技术手段寻找园区内大气污染源最优的监测路径，是本文重点解决的问题。

不同于传统的多旅行商（mTSP）问题，该方法根据农业园区污染源监测的特定问题来构建目标函数和约束条件，目标函数中考虑了各无人机监测路径总长度最短、无人机飞行路径转弯角最小（保证飞行的平滑度以减少无人机飞行能耗）、无人机对障碍物的躲避半径最大（该项可使得无人机距离障碍物的路径适应度值小，以保证最终得到的路径和障碍物保持一定距离）；特定的约束条件包括单架无人机续航时间限制、各污染源排放污染物类别和排放污染物数量限制、各污染源无人机停留时间限制、无人机起飞出发点和终点限制等。而后采用基于复杂变异树的多染色体遗传算法来对上述规划模型进行求解，得到最优的农业园区污染源监测路径。

1 优化方法

该方法首先获取目标农业园区的环境信息，所述环境信息包括无人机出发基地和n个污染源位置的坐标信息、单架无人机续航时间、无人机平均飞行速度、无人机飞行单位能耗、无人机悬停单位能耗、各污染源排放污染物类别和排放污染物数量、各污染源无人机停留时间、无人机数目m等；而后根据农业园区的环境信息构建大气污染源监测的路径优化问题模型，设定模型的特定目标函数和约束条件；最后基于复杂变异树的多染色体遗传算法来对上述规划模型进行求解，得到多个无人机最优的农业园区污染源监测路径；目标函数F为：

minF=w1·L/Lmax+w2·Dmax/D+w3·θ/θmax，

式中，w1，w2和w3为监测路径总长度L、无人机对障碍物的躲避半径D、无人机飞行路径转弯角θ的三个子目标的权重，w1+w2+w3=1；Lmax、Dmax和 θmax为预先设定的极大值，目的为去量纲化。躲避半径D取倒数的原因是我们期望无人机躲避半径越大越好。

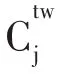
式中，Dm为第m架无人机的飞行路径对障碍物的躲避半径之和，g为障碍物的数量，dk为飞行路径距离第k个障碍物的距离，rk为障碍物的最大外围半径。

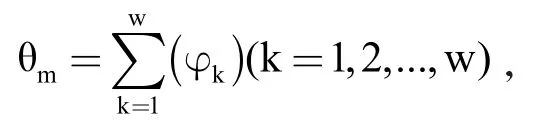
式中，θm为第m架无人机的飞行路径上转弯角之和，w为转弯角的数量，φk为飞行路径上第k个转弯角。

步骤S2的约束条件为：遍历农业园区内所有污染源监测点、无人机起飞基地和终点基地均为出发点：

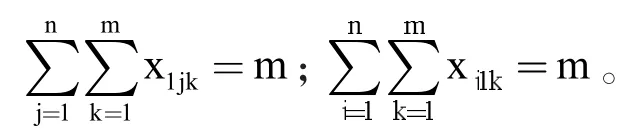
每个污染源仅停留一次：

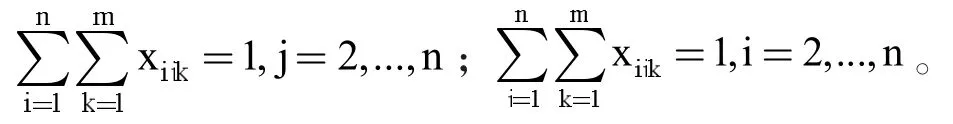
单架无人机续航能力和其他约束：

式中，M为预先给定的无人机数量；m为优化后的无人机数量。

2 优化步骤

面向农业园区污染源监测的多无人机路径优化方法的计算过程如图1所示。具体过程如下：（1）设置基于复杂变异树的多染色体遗传算法的参数，包括种群数量Pop、迭代次数S、无人机数量（即染色体数量）M；（2）初始化种群，根据当前染色体数量M，采用多染色体编码的方式对种群进行编码，一条染色体代表一架无人机的污染源监测点序列；计算算法适应度函数；（3）随机选择复杂变异树中不同复杂程度的算子，对各种群进行优化，复杂变异树分为简单变异算子、一般变异算子和复杂变异算子。简单变异算子包括交换（Swap）算子、倒位（Reverse）算子、滑动（Slide）算子、插入（Insert）算子和交叉（Crossover）算子；一般变异算子为随机两个简单算子结合而成，包括交换和交叉（Swap & Crossover）算子、逆转和交叉（Reverse & Crossover）算子、滑动和交叉（Slide & Crossover）算子、插入和滑动（Insert & Slide）算子、插入和交叉（Insert & Crossover）算子；复杂变异算子为随机三个简单算子结合而成，包括Swap & Reverse & Crossover算子、Slide & Insert & Crossover算子、Swap & Slide & Crossover算子、Slide & Reverse & Crossover算子；（4）判断当前迭代次数是否达到最大迭代次数S，若达到，则记录当前最优解；否则，返回。（5）判断当前无人机数量（染色体数量）是否达到下限，若达到，则输出当前最优解；否则，无人机数量-1，返回。

图1 多无人机路径优化算法计算步骤

3 案例计算

该实例中需要解决的技术问题为：已知某农业园区内各个污染源的位置坐标信息和各污染源排放污染物类别和污染物排放数量，以监测区域的中心点为无人机出发基地，m架无人机航行到n个大气监测点，最终回到出发基地；每架无人机可到多个监测点进行采样监测，要求每个监测点都被采样监测且每个监测点只能被一架无人机采样，根据各污染源排放污染物类别和排放污染物数量确定其采样停留时间，m架无人机需要在完成监测任务后再回到出发基地，要求为每架无人机规划出最优的监测路径，且无人机数量最终达到最优化。已知目标农业园区占地面积为36km2，园区内随机分布有20个排放污染源，20个污染源的坐标信息、污染物排放类型和无人机停留时间为已知条件；单架无人机续航时间为 40min，平均飞行速度为 5m/s；w1取 0.95，w2取 0，w3取0.05；种群数量Pop设定为80，迭代次数设定为500，初始无人机数量预设为8架。利用基于复杂变异树的多染色体遗传算法来对上述规划模型进行求解，最终得到多个无人机最优的农业园区污染源监测路径，见图2。

图2 农业园区污染源监测路径MATLAB仿真结果

由图2可知，优化后的无人机数量为6架，第1架无人机的航行路径为1→18→2→1，第2架无人机的航行路径为1→15→20→1，第3架无人机的航行路径为1→12→19→1，第4架无人机的航行路径为1→16→17→11→10→1，第5架无人机的航行路径为1→6→5→14→1，第6架无人机的航行路径为1→4→9→13→3→8→1；6架无人机的飞行路径总长度为49.0073km，计算程序的迭代次数为435次。由计算结果可知，该方法可用于解决农业园区污染源监测的多无人机路径优化问题。