暴雨作用下含裂缝谭家湾堆积层滑坡渗流特征与稳定性分析

李林均，简文星，张端淼，董志鸿，张 彬，潘永亮

(1.中国地质大学(武汉) 工程学院，湖北 武汉 430074；2.宜昌市地质环境监测站，湖北 宜昌443000;3.湖北冶金地质研究所(中南冶金地质研究所)，湖北 宜昌 443003;4.湖北省地质环境总站应急中心，湖北 武汉 430034)

三峡库区地质构造复杂，岩性组成多样，降雨丰富且暴雨频发，是我国滑坡灾害发生频繁的重灾区之一。在库区各种类型滑坡灾害中，堆积层滑坡分布广泛，数量众多，所占比例较大，仅在长江上游地区100万km范围内发育的1 736个滑坡中就有64%为堆积层滑坡。堆积层滑坡特殊的物质组成及结构特征，决定了降雨及地下水的作用常常是导致其变形、甚至失稳最主要的动因。据统计，秭归县50万m以上受降雨激发的158处滑坡中堆积层滑坡为149处,占比达94%。因此，研究降雨作用下三峡库区典型堆积层滑坡的渗流场和稳定性变化规律十分必要。

已有研究表明，降雨可引起滑坡渗流场的变化，雨水入渗一方面使滑坡土体含水量增大、基质吸力降低，从而引起抗剪强度减小，另一方面使滑坡土体孔隙水压力增大、有效应力降低，此外还可使滑带饱和后软化、强度降低。现有入渗理论认为，当降雨强度达到滑坡表层土体积水点之后，过强的降雨将转化为地表径流，雨强的增大并不会相应地增加入渗量，因此均质土坡中降雨入渗的影响深度极为有限。而通过对三峡库区大量堆积层滑坡实例研究发现，降雨强度越大，堆积层滑坡的规模也越大，当降雨强度为120 mm/d时可触发中厚层堆积层滑坡，当降雨强度为150 mm/d时可触发大型厚层堆积层滑坡。可见，雨水渗入深层土体触发大型滑坡的机制仍存在争议。对于大多数滑坡，在发生整体滑移前往往会产生比较显著的变形，尤其在滑坡中后部会产生一系列拉张裂缝；在暴雨作用下拉张裂缝处可以迅速形成优势入渗，从而增强暴雨对其稳定性的影响。

目前，不少学者已经开展了降雨作用下具有裂缝斜坡的渗流场与稳定性评价方面的研究工作。如姚海林等、张维等、Zhang等对降雨作用下含裂隙的膨胀土边坡渗流场与稳定性进行了研究；魏凌傲等、万思豪等分析了不同降雨类型下裂隙各向异性对膨胀土边坡渗流场的影响；祝磊等、张毅等对降雨入渗作用下不同裂隙和风化深度的煤系土边坡的渗流场进行了数值计算和分析；Zhang等利用有限元数值软件再现了暴雨作用下川东红层近水平基岩滑坡后缘裂缝充水导致其失稳前的渗流场特征，并以此为基础计算了在暴雨作用过程中坡体稳定性的变化情况；蒋泽锋等将边坡临界滑动场法与降雨入渗条件下饱和-非饱和渗流分析相结合，考虑了张裂缝在降雨入渗及充水状态下对均质黏土边坡稳定性的影响。

通过以上研究，人们已经认识到降雨作用下裂缝对不同类型岩土体渗流场与稳定性有重要的影响。但是，对于大型堆积层滑坡，以往的研究在考虑降雨过程中其渗流场与稳定性演化规律时往往没有量化拉张裂缝的不利影响，且在其稳定性评价时没有对滑带饱水后的动态软化加以考虑。为此，本文通过地质调查、位移监测数据分析以及数值模拟方法，对三峡库区谭家湾堆积层滑坡在暴雨作用下考虑裂缝优势入渗时的瞬态渗流场与稳定性演化规律进行研究，以期对暴雨诱发大型深层堆积层滑坡的机制及其防治工作提供一定的参考。

1 滑坡概况与地质背景

谭家湾滑坡位于湖北省秭归县水田坝乡，距三峡大坝43 km。滑坡地处秭归向斜核部长江北岸单斜顺层斜坡，属侵蚀构造低山地貌类型，地势南西高北东低。滑坡后缘高程为360 m，前缘最低高程为170 m左右，相对最大高差为200 m；滑坡平面形态呈“舌”形(见图1)；滑坡主滑方向为68°，最大纵长约440 m，平均宽为295 m，滑体平均厚约25 m， 分布面积约为11.3×10m，体积约为282.5×10m，属大型深层堆积层滑坡。

谭家湾滑坡滑体主要为含碎石粉质黏土，呈黄褐-红褐色，稍湿，可塑-硬塑，土石比约为7∶3～9∶1，碎石直径一般为1～5 cm，大者可达8～20 cm，碎石成分主要为泥质粉砂岩、石英砂岩；滑带主要物质成分为黄褐色含砾粉质黏土，软塑-可塑状，土石比为9∶1，砾石成分主要为紫红色泥质粉砂岩、灰黄色石英砂岩，呈棱角-次棱角状，粒径约为0.2～0.4 cm，滑带厚度约20～40 cm，平均厚度为30 cm；滑床为侏罗系上统蓬莱组(J

p

)地层，岩性为石英砂岩、紫红色砂岩、泥岩不等厚互层，厚层状构造。谭家湾滑坡典型工程地质剖面图见图2。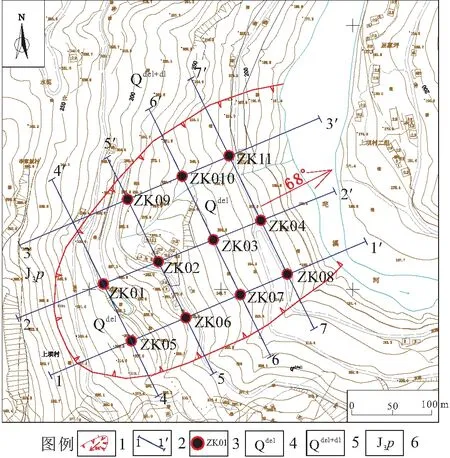

图1 谭家湾滑坡工程地质平面图Fig.1 Engineering geological plan of Tanjiawan landslide1.滑坡边界；2.剖面线及编号；3.钻孔及编号；4.第四系滑坡堆积层；5.第四系残坡堆积层；6.侏罗系上统蓬莱镇组

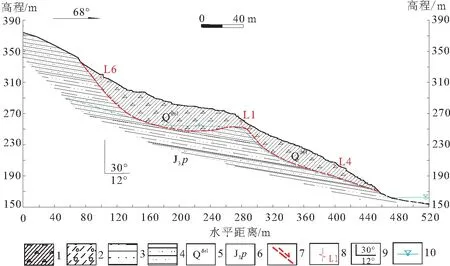
图2 谭家湾滑坡典型工程地质剖面图Fig.2 Typical engineering geological section of Tanjiawan landslide1.含碎石粉质黏土；2.卵石夹石粉质黏土；3.泥质粉砂岩；4.石英砂岩；5.第四系滑坡堆积层；6.侏罗系上统蓬莱镇组；7.滑带及滑动方向；8.裂缝及编号；9.岩层产状；10.推测地下水水位线

2 含裂缝谭家湾滑坡变形特征分析

2.1 滑坡宏观变形分析

谭家湾滑坡第一次较大规模的变形发生于2014年夏季的一次强降雨过程，此后2017年和2018年的6～10月份强降雨时段，均有不同程度的变形迹象产生。根据现场调查，谭家湾滑坡中后部发育多条弧形裂缝并伴有局部下挫，最大裂缝LF1长约135 m，拉张约5～50 cm[见图3(a)]，最大下挫高度约120 cm；滑坡中前部变形最强烈区段公路路基有显著下沉，路面已完全破损，整体下凹，并向滑动方向轻微凸出，公路损毁段长约10 m，变形约3～5 m，下沉为1～1.5 m，该段公路下方坡体发生鼓胀变形[见图3(b)]。

图3 谭家湾滑坡变形特征Fig.3 Deformation characteristics of Tanjiawan landslide

2.2 滑坡位移监测数据分析

据《三峡库区秭归县地质灾害监测预警工程专业监测年报》相关的监测数据显示，谭家湾滑坡的专业监测手段包括GPS地表位移监测、裂缝位移监测两类。谭家湾滑坡近十年地表累计位移、近三年地表裂缝(LF1)位移以及降雨量随时间的变化曲线如图4所示。

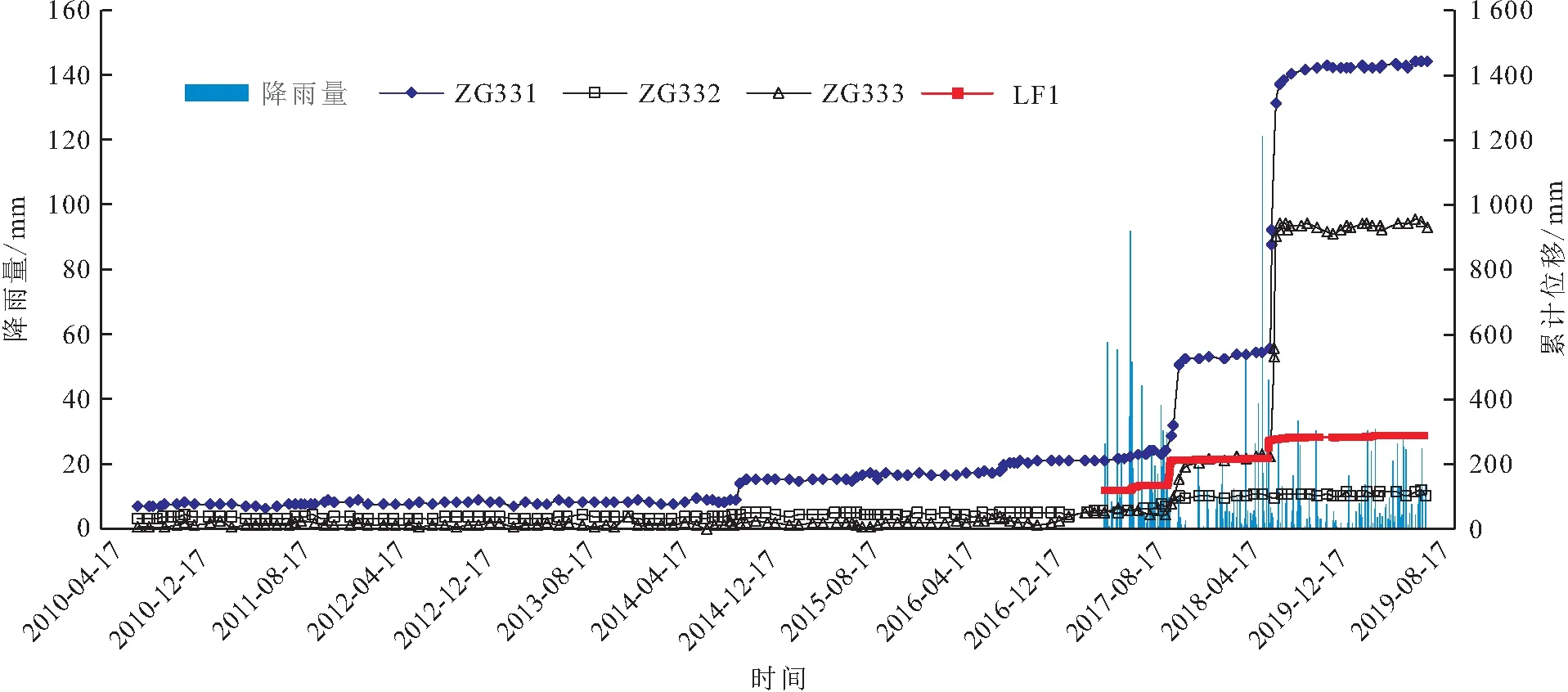
图4 谭家湾滑坡GPS地表位移监测点、裂缝(LF1)监测点累计位移以及降雨量随时间变化的关系曲线Fig.4 Correlation curves of rainfall and accumulative displacement of GPS monitoring points and crack monitoring points in Tanjiawan landslide with time

由图4可以看出:

(1) 在监测时段内3个GPS地表位移监测点中位于滑坡中部和前部的测点ZG331、ZG333分别发生了2次、3次较大的变形，累计地表位移-时间曲线具有明显的阶跃特征，台阶高度在历次变形中逐次增大，且历次变形均发生在降雨量丰富的6～10月份，尤其是在2017年9～10月份持续性降雨时段，2018年6～7月份强降雨时段。

(2) 在该强降雨时段内，裂缝位移-时间曲线同地表位移-时间曲线一样呈现明显的阶跃式抬升。以2018年监测数据为例，滑坡中部测点ZG331、前部测点ZG333的年度累计水平位移分别为894.5 mm、723.7 mm，在6月份之前累计水平位移-时间曲线较为平缓，随后在6月18日至7月9日强降雨时段内出现2次日降雨量高于40 mm的强降雨过程，且降雨量最大值高达121.6 mm(6月18日)，累计水平位移在该时段内的增量分别达到754.3 mm、683.7 mm；位于滑坡中部的裂缝监测点显示在该年度内裂缝宽度累计增加值为66.8 mm，位移速率为5.6 mm/月，最大日位移速率为34.1 mm/d，发生于7月6日；而滑坡后部测点ZG332的年度累计水平位移值仅为4.7 mm，位移速率为0.4 mm/月，可认为几乎没有发生位移变化。

通过以上分析可知，谭家湾滑坡地表GPS位移监测点的变形特征与地表裂缝位移特征基本吻合，滑坡变形区域主要集中在滑坡中前部，可能与滑坡中部基岩上凸的特殊形态有关；滑坡变形对强降雨过程十分敏感，且历次变形均集中发生于降雨后一段时间内，滑坡稳定性具有逐年弱化的趋势。

3 含裂缝谭家湾滑坡渗流特征与稳定性数值模拟计算分析

3.1 数值模型建立

综合考虑谭家湾滑坡的工程地质特征、监测点分布情况和滑坡变形特征，以该滑坡2-2′主滑剖面为计算剖面建立二维数值模型，采用数值模拟软件GEO-STUDIO分析暴雨条件下考虑裂缝优势入渗时谭家湾滑坡的渗流场与稳定性演化规律。该滑坡数值模拟计算模型见图5。

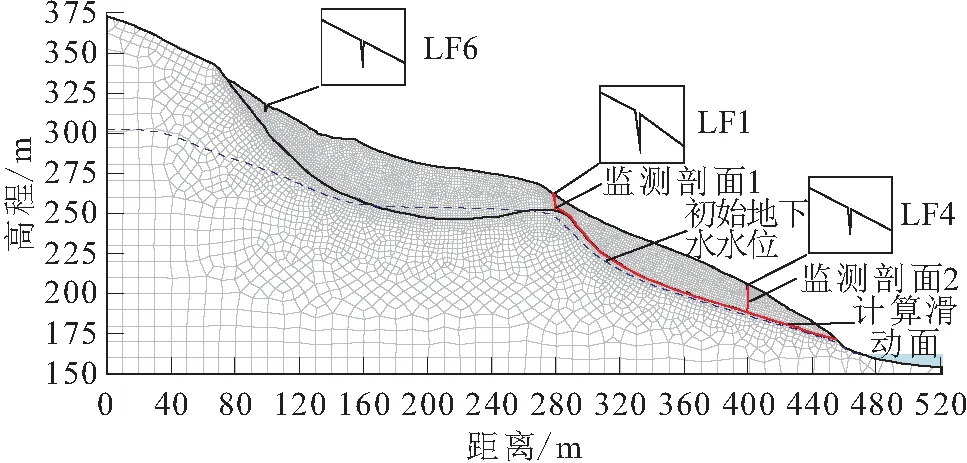
图5 谭家湾滑坡数值模拟计算模型Fig.5 Numerical simulation calculation model of Tanjiawan landslide

(1) 初始状态与边界条件：秭归地区多年平均年度总降雨量为1 028.6 mm，平均至每天为2.8 mm，将其作为初始流量边界；根据谭家湾滑坡勘察资料可知，滑坡中后部钻孔ZK02、ZK03揭露地下水水位埋深分别为23.3 m、17.7 m，勘察期间滑坡前缘归州河水水位高程为162.4 m，据此对滑坡地下水水位初始水头边界条件进行反演试算，最终将模型左侧定水头边界设置为302.5 m，右侧定水头边界设置为162.4 m，以此确定初始地下水水位；滑坡前缘剪出口到归州河面设置为潜在溢出面，坡面设置为单位流量边界模拟降雨，其余边界均为不透水边界。在此基础上进行滑坡渗流场稳态数值模拟计算，并将所得渗流场结果作为模型的初始渗流场状态。

(2) 裂缝的设置：目前利用数值方法对裂缝进行模拟的方式较多，本文利用文献[24]、[25]的思路，将裂缝两侧视为边界，把裂缝从滑体区域去除，引入边界条件，并对裂缝边界处网格进行加密。根据野外调查的实际情况对模型进行简化，仅在滑坡后缘(

x

=99.6 m)、中部(

x

=278.9 m)和前部(

x

=400.2 m)设置3条主要拉张裂缝，不考虑次要裂缝，滑坡中部裂缝宽度为0.4 m、深度为3 m，滑坡后缘和前部裂缝宽度为0.3 m、深度为2 m。

(3)材料参数：利用SEEP/W渗流模块进行滑坡渗流场模拟时，需要提供滑坡岩土体饱和渗透系数和饱和体积含水量这两个重要的水力学参数，谭家湾滑坡岩土体饱和渗透系数和饱和体积含水量通过勘察资料与工程类比获得，具体取值见表1。基于滑坡岩土体饱和体积含水量采用SEEP/W渗流模块自带的样本函数类比可以获取土-水特征曲线，在此基础上结合滑坡岩土体饱和渗透系数与Frellund&Xing模型拟合,便可以得到滑坡岩土体渗透系数函数，滑坡岩土体渗透系数、基质吸力及体积含水量的关系式如下：

(1)

式中：

K

为计算所得土体非饱和渗透系数(m/s);

K

为测得的土体饱和渗透系数(m/s);

θ

为土体体积含水量(无量纲)；

θ

′为土体体积含水量的一阶导数；

θ

为土体饱和体积含水量(无量纲)；

y

代表基质吸力算法的虚拟度量；

i

为

j

到

N

之间的数值距离；

ψ

为对应第

j

步的土体基质吸力(kPa)；

j

为最终函数描述的土体最小基质吸力(kPa)；

N

为最终函数描述的土体最大基质吸力(kPa);e为自然对数的底2.718 28。

此外，根据实际地层情况，并结合勘察资料室内实验结果以及三峡库区秭归段相似工程类比，综合分析赋予谭家湾滑坡岩土体各层材料物理力学参数，具体数值见表1。

表1 谭家湾滑坡岩土体物理力学参数

3.2 计算方案

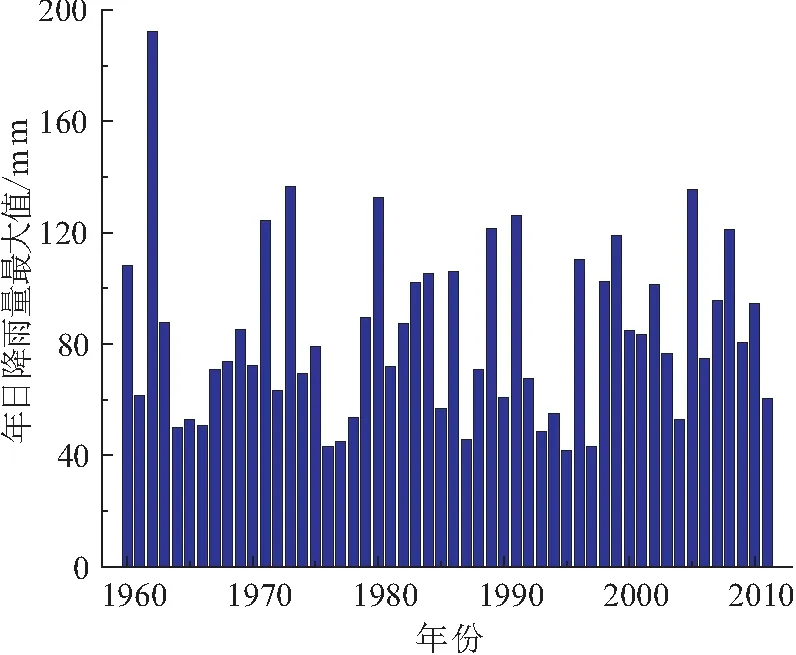
图6 秭归县最大日降雨量直方图 (1960—2011年)Fig.6 Histogram of maximum daily rainfall in Zigui district(1960-2011)

秭归地区降雨丰富，是三峡库区两个暴雨中心地带之一，前人根据该区域1960—2011年日降雨量最大值统计数据(见图6)，并基于皮尔逊Ⅲ型曲线，采用数理统计的方法得到秭归地区10 a、20 a、50 a、100 a一遇日降雨强度分别为125.6 mm、142.9 mm、164.5 mm、180.2 mm。结合近年来极端降雨天气日益频现的趋势，同时为了体现出暴雨过程中滑坡从非积水入渗到坡体裂缝内产生积水，再转换为积水入渗的过程，选择以上极端降雨统计结果作为本次数值模拟的暴雨工况；降雨过程持续4 d，其中0～1 d为10 a一遇暴雨，1～2 d为20 a一遇暴雨，2～3 d为50 a一遇暴雨，3～4 d为100 a一遇暴雨；前3 d降雨强度小于滑体饱和渗透系数，无积水产生，裂缝设置为单位流量边界，第4 d降雨强度大于滑体饱和渗透系数，认为裂缝处迅速形成积水，裂缝边界按定水头边界处理，积水深度为裂缝深度；同时在降雨停止后保持6 d不降雨的情况。

3.3 暴雨作用下含裂缝谭家湾滑坡渗流特征分析

为了便于对暴雨作用下含裂缝谭家湾滑坡的渗流特征进行分析，在滑坡中部(

x

=278.9 m)和前部(

x

=400.2 m)裂缝处设置两个监测剖面(见图5)，分别为监测剖面1、监测剖面2；图7和图8给出了整个暴雨过程中监测剖面处特定深度滑坡岩土体的体积含水量、孔隙水压力随时间的变化情况。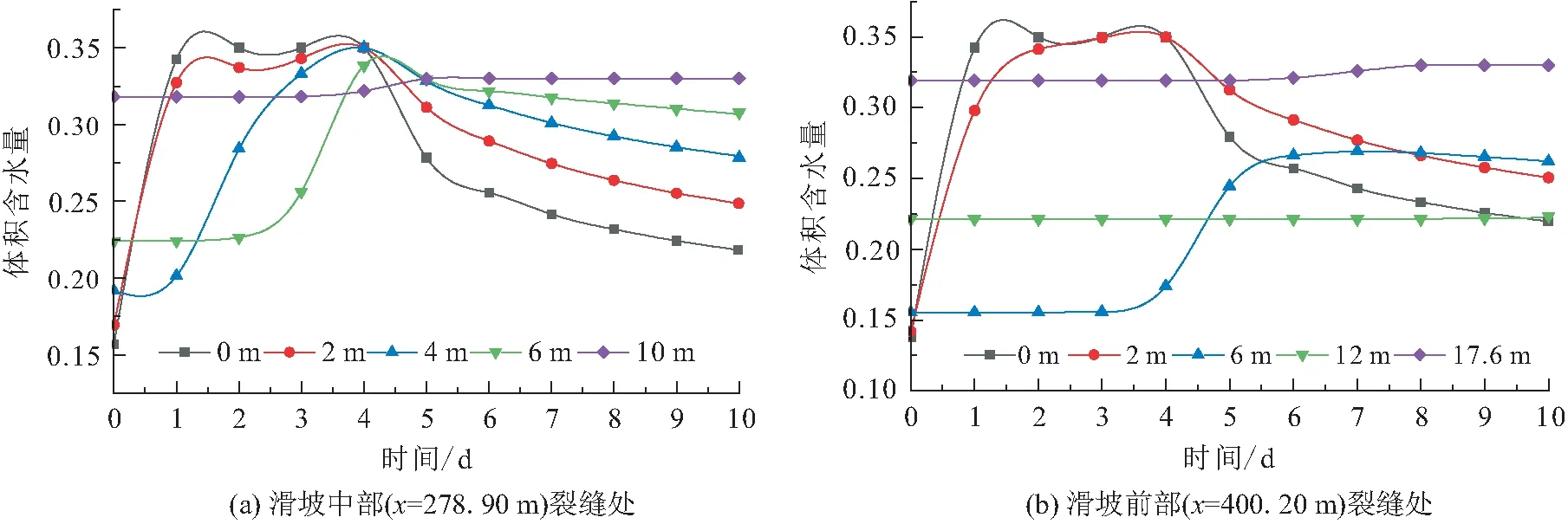

图7 暴雨作用下滑坡裂缝不同埋深处滑体体积含水量随时间的变化曲线Fig.7 Variation curves of volumetric water content of sliding mass of different depths of fracture profile with time under rainstorm

图8 暴雨作用下滑坡裂缝不同埋深处滑体孔隙水压力随时间的变化曲线Fig.8 Variation curves of pore water pressure of sliding mass at different depths of fracture profile with time under rainstorm

3.3.1 滑坡裂缝处滑体体积含水量变化特征

由图7可见，由于初始地下水的影响，滑体初始体积含水量随埋深的增加逐渐增大，滑坡中部基岩向上微凸的特殊地质结构导致中部的滑体较薄，地下水埋深较浅，因此滑坡中部裂缝处滑体的初始体积含水量相较于滑坡前部裂缝处滑体同一深度处的更大；在暴雨开始后，滑坡裂缝处地表土体体积含水量迅速升高，尽管前3 d降雨强度小于滑体饱和渗透系数，但在暴雨持续2 d后滑坡裂缝处地表土体均达到了饱和；滑坡中部裂缝埋深6 m处滑体体积含水量对暴雨开始时刻的响应延迟时间为3 d，较滑坡前部裂缝处滑体同样深度处提前了1 d；暴雨结束时，滑坡前部裂缝处埋深2 m、滑坡中部裂缝处埋深4 m内的滑体均达到完全饱和状态，可见此时滑坡裂缝处一定深度范围内均形成了瞬态饱和区域，且滑坡中部裂缝处的饱和区域更大；暴雨结束6 d后，滑坡前部裂缝处埋深为12 m处滑体体积含水量无变化，即使存在裂缝，雨水入渗影响范围也未到达该深度，但埋深17.6 m(滑带位置)处滑体体积含水量在暴雨降雨结束4 d后增长到0.33，由非饱和状态转变成饱和状态；滑坡中部裂缝处雨水入渗影响深度则直达基覆界面滑带处，并且滑带在降雨结束后1 d时便已达到了饱和。

3.3.2 滑坡裂缝处滑体孔隙水压力变化特征

由图8可见，滑坡裂缝不同埋深处滑体的孔隙水压力变化规律与体积含水量变化规律类似；在暴雨持续的前3 d内，因降雨强度小于滑体饱和渗透系数，裂缝深度内无积水产生，滑体孔隙水压力一直未超过0 kPa；到暴雨持续第4 d时，降雨强度大于滑体饱和渗透系数，裂缝深度内瞬态饱和区域产生积水，积水深度随裂缝深度线性增加，滑坡中部和前部裂缝底部积水深度分别达到3 m、2 m，相应的滑体孔隙水压力值分别为30 kPa、20 kPa，并且裂缝底部外1 m处孔隙水压力均大于0，分别达到6.7 kPa、1.7 kPa；暴雨结束1 d后，滑坡中部裂缝下部滑带(10 m处)已达到饱和，由于雨水继续下渗，该处滑体孔隙水压力持续增大，在暴雨结束4 d后滑体孔隙水压力从初始状态时的-10.2 kPa升高到最大值15.7 kPa，增幅高达253.9%，地下水水位涨幅为2.6 m。此外，在整个暴雨过程中，滑坡前部裂缝在埋深12 m处滑体孔隙水压力一直保持为-46.2 kPa，但是在埋深17.6 m(滑带位置)处暴雨结束4 d时已达到饱和，滑体孔隙水压力值在暴雨结束6 d后达到最高值8.6 kPa。

3.3.3 裂缝优势入渗对谭家湾滑坡渗流场的影响机制分析

前文所述较为清晰地反映了暴雨作用下含裂缝谭家湾滑坡的裂缝优势入渗过程，可见在连续极端暴雨工况下谭家湾滑坡所发育的3条主要拉张裂缝(尤其是滑坡中部裂缝)作为优势入渗通道对滑体内的渗流场有显著的影响。本文分析其原因认为：一是由于堆积层滑坡发育的拉张裂缝扩大了雨水入渗边界，裂缝侧壁直接受到暴雨的影响，地表与开裂深度范围内滑坡土体共同接受雨水的补给，入渗量增大导致土体含水量快速增加，裂缝处地表土体饱和时间提前；二是因为当暴雨强度超过滑坡地表土体饱和渗透系数之后，此时入渗能力由滑体饱和渗透系数决定，雨水将会沿着地表顺坡向径流排泄，裂缝的存在导致径流的雨水通过裂缝汇集直接渗入滑体内部，缩短了渗流路径，流动的雨水在滑体开裂深度内扩散速度快，导致土体基质吸力迅速降低，并在裂缝处一定范围内快速形成瞬态饱和区域；该区域在雨水的持续补给下迅速形成积水，且积水深度随裂缝的深度线性增加，积水有压渗透显著增加了入渗速度与入渗量，使得入渗影响范围扩大。此外，滑坡中部基岩向上突起的特殊地质结构导致中部裂缝处滑体厚度较薄，裂缝底部距离地下水水位较近，土体初始体积含水量较高，因此暴雨作用下雨水通过滑坡中部裂缝入渗速度更快，响应范围更广，更易直接补给入地下水，使滑带处地下水水位大幅度升高，在水头差作用下地下水沿滑带处顺坡向流动，从而引起滑坡前部裂缝处雨水入渗影响极限深度之外的滑带(埋深为17.6 m)位置在降雨结束6 d后地下水水位涨幅接近1 m。

3.4 暴雨作用下含裂缝谭家湾滑坡稳定性分析

将上节所得暴雨条件下含裂缝谭家湾滑坡瞬态渗流场计算结果导入GEO-SLOPE/W模块，可以得到暴雨过程中滑体不同时刻的暂态孔隙水压力分布情况，基于Fredlund非饱和土强度理论，利用Vanapalli等提出的方程可以计算出暴雨过程中滑带的非饱和抗剪强度，具体方程如下：

(2)

式中:

τ

为非饱和土体抗剪强度(kPa)；

c

′为土体有效黏聚力(kPa)；

φ

′为土体有效内摩擦角(°);(

σ

-

u

)为破坏面上土体的净法向应力(kPa)；(

u

-

u

)为破坏面上土体的基质吸力(kPa)；

θ

为土体体积含水量；

θ

为土体饱和体积含水量；

θ

为土体残余体积含水量。此外，暴雨入渗后导致地下水水位升高，滑带在地下水渗流与浸泡软化作用下微观结构损伤引起强度大幅度降低，且其强度会随饱和时间的延长进一步劣化，在滑坡稳定性计算时须予以考虑。因此，假定滑带土饱和抗剪强度指标

c

和

φ

随饱和时间的变化关系为

S

(

t

)=

α

(

t

)·

S

(0)

(3)

式中:

S

(

t

)为饱水时长

t

时滑带土抗剪强度参数

c

或

φ

值；

S

(0)为初始饱和时刻(

t

=0)滑带土抗剪强度参数

c

或

φ

值；

α

(

t

)为滑带土抗剪强度随饱和时间的衰减因子。谭家湾滑坡滑带土的强度衰减因子通过工程类比选用文献[31]对秭归千将坪滑坡滑带土在不同饱水时长下的抗剪强度试验数据计算所得，千将坪滑坡与谭家湾滑坡距离较近，且两者均发育于侏罗系地层，其滑带土为侏罗系中统炭质页岩夹层剪切泥化形成的黄褐色粉质黏土，对谭家湾滑坡基覆界面处含侏罗系上统泥岩角砾的黄褐色粉质黏土滑带具有一定的借鉴意义。采用指数函数模型对试验数据进行拟合后得到滑坡滑带土黏聚力

c

和内摩擦角

φ

的

α

(

t

)随饱水时间的变化规律分别符合如下模型：

α

(

t

)=0.60+0.40e-0.05

(4)

α

(

t

)=0.77+0.23e-0.05

(5)

谭家湾滑坡滑带土天然强度和初始饱和强度取值见表1，结合公式(3)～(5)可实现暴雨结束后处于不同饱和软化时长下的谭家湾滑坡滑带土强度参数的动态取值。在以上基础上,结合极限平衡法中的Morgenstern-Price法，可对在整个暴雨过程中同时考虑暂态正负水压力及软化作用下的谭家湾滑坡稳定性进行计算。需要指出的是，由于该滑坡上、下部滑动面不是统一的整体，难以整体滑动，且变形主要集中在滑坡中前部，因此滑坡稳定性计算时滑动面设置为从滑坡中部裂缝进入沿基覆界面至前缘剪出(见图5)。此外，在计算过程中滑坡滑带土的饱和软化时长根据第3.3.1节滑坡裂缝处滑体体积含水量监测剖面来确定，由滑坡中部裂缝处滑体体积含水量监测剖面数据[见图7(a)]可知，监测剖面1底部滑带土在暴雨持续的1～4 d内均为非饱和状态，因此在暴雨持续过程中滑坡稳定性计算采用滑带土天然抗剪强度参数；降雨结束1 d时(第5 d)，滑坡中部裂缝监测剖面底部滑带土已达到饱和，此时地下水水位已升高到滑带以上，并且形成较高的水头将促使地下水沿滑带向下快速渗流，滑坡下部滑带土也将迅速饱和。因此，为了便于取值计算，基于最不利工况假设，在第5 d时，假设滑带土全部达到饱和，统一采用初始饱和强度参数；随后第6 d至第10 d，假设滑坡滑带土饱水时长分别为1 d至5 d，从而可采用公式(3)～(5)对相应饱水时长下滑带土的强度参数依次进行计算，最终计算得到滑坡稳定性系数与降雨持时的关系见图9。

图9 谭家湾滑坡稳定性系数与降雨持时的关系曲线Fig.9 Relationship curve between stability factor of Tanjiawan landslide and rainfall duration

由图9可见，随着暴雨过程的持续，滑坡稳定性系数逐步下降，这是由于随着雨水的入渗，滑体含水量增加、基质吸力减小，降低了土体的抗剪强度；在暴雨持续4 d的过程中，暴雨强度大于滑体饱和渗透系数，雨水径流汇入滑体表面拉张裂缝形成的积水入渗大幅度增加了雨水在滑体内的入渗速度、入渗量，使滑体基质吸力下降速度加快，滑体基质吸力降低的范围扩大，从而引起滑坡稳定性系数下降幅度与下降速度开始增大；降雨结束1 d后，由滑坡中部裂缝处滑体体积含水量和孔隙水压力的监测数据(见图7和图8)可知，下渗的雨水升高了地下水水位使滑带土开始饱和，强度软化降低，且其孔隙水压力持续增大，因此滑坡稳定性系数出现大幅度下降；随后地下水持续向下渗流形成动水压力，并且滑带土的饱水时长不断增加，导致滑带土微观结构损伤，强度进一步劣化，引起滑坡稳定性系数持续降低；到暴雨结束6 d后，滑坡前部裂缝处滑体孔隙水压力监测剖面[见图8(b)]显示，该剖面底部滑带处土体孔隙水压力此时达到最高，并且滑带土在持续饱水软化5 d后强度衰减达到最低，导致滑坡稳定性系数达到最低值0.997，此时滑坡处于不稳定状态。由此可见，连续极端暴雨作用下谭家湾滑坡后缘、中部和前部发育的3条主要拉张裂缝处形成的优势入渗对该滑坡的稳定性极为不利。

4 结论与建议

(1) 谭家湾滑坡在天然条件下处于稳定状态，其变形主要集中在滑坡中前部，且与强降雨过程紧密相关；滑坡地表累计位移-时间曲线与裂缝累计位移-时间曲线呈明显的阶跃特征，前期形成的拉张裂缝对其变形有不利影响，在降雨等因素的影响下滑坡稳定性具有进一步弱化的趋势。

(2) 在暴雨条件下，拉张裂缝对谭家湾滑坡渗流场与稳定性的影响较为显著，裂缝一方面扩大了堆积层滑坡的入渗边界，缩短了入渗路径；另一方面当降雨强度大于滑体饱和渗透系数之后，地表径流的雨水汇入裂缝，使裂缝深度内土体快速饱和，形成积水后转变为有压入渗，大幅度增加了雨水的入渗速度、入渗量。

(3) 在暴雨条件下，拉张裂缝的发育部位对谭家湾滑坡渗流场的影响程度存在较大的差异。当裂缝发育处滑体厚度较薄、距离地下水水位较近时，雨水通过裂缝更易直接补给地下水，引起滑带处地下水水位的大幅度升高，滑带土持续浸泡软化后导致滑坡稳定性大幅度且持续性地降低。

(4) 三峡库区降雨丰富，堆积层滑坡发育数量大且分布广泛，在库区堆积层滑坡勘察、监测及防治工作中需加强对滑坡地表拉张裂缝的详细调查并采取相应的封闭措施，以防止雨水通过裂缝大量入渗对堆积层滑坡稳定性造成不利的影响。