深基坑多层承压含水层中混合井降水技术优化研究

张哲斐，冯晓腊,2，蔡兵华，陈 帅，刘旭阳

(1.中国地质大学(武汉)工程学院，湖北 武汉 430074；2.武汉丰达地质工程有限公司， 湖北 武汉 430074；3.武汉市政建设集团有限公司，湖北 武汉 430074)

承压含水层水头高、水量大、补给迅速，尤其对于深基坑多层含水系统地下水控制问题，若盲目采用降水措施，由此诱发的地面沉降以及对周边环境的影响问题是不容忽视的。因此，常采用降低承压水水位的方式来控制承压水对基坑工程的不利影响。

目前，针对深基坑地下水控制方法已有大量的研究。如程芸等以武汉长江隧道基坑为例，利用正交试验和数值模拟方法分析了存在止水帷幕情况下地下水渗流场特点和黏土层释水固结特征；马郧等以富水复杂环境地质条件下的深基坑为例，提出布设在下部强透水层中的降水井深度要适当，并非其越深降水效果越好；陈崇希建立了地下水定流量降水井抽水的稳定混合井流和不稳定混合井流两种模型，对比Hantush、Neuman关于混合观测孔水位建议方程所需要的条件，研究得出混合抽水井各层流量的分配与各层的导水系数成正比；Ai等针对渗透各向异性层状地层中的点源抽水问题进行了求解分析，重点分析了渗透各向异性地层对孔压的影响；Barzegar等通过对伊朗大不里士平原水文地质条件的调查，发现平原中部存在无限含水层和承压含水层，而靠近高地地区只有无限含水层，且承压含水层存在轻微渗漏；曹洪等以沙金煊提出的承压非完整井中滤管顶或底位于含水层中的理论推导为基础，假设上下部渗流场中深井滤管长度与其含水层厚度的比值相等，得到适用于滤管顶、底均不在含水层层面的承压非完整井的近似计算方法；王军辉等以北京地区为例，通过建立渗流-压缩耦合数学模型，提出采用主控含水层来确定耦合模型下边界的新方法；李佐春等以太原地铁2号线某站采集水样测得的含砂量数据为基础，从滤网类型、滤料、井管和降水井实时出水量等方面分析了管井降水中出水含砂量的影响因素；Zhao等通过对多层含水层中14个抽水试验数据联合反演水文地质参数，将估计的含水层渗透系数

K

和储水率

S

参数用于另一种泵送测试的正向仿真系统，从而合理计算出含水层的水文地质参数。

综上所述，国内外对深基坑地下水控制方法已有大量的研究，但由于工程特点不一，降水方案也不相同，应进一步围绕降水管井进行深入研究。

本文基于荆州市某深基坑工程现场试验数据，采用理论计算与数值模拟相结合的方法，通过改进“降水井滤管”在两层承压含水层中的数量、长度以及分布位置，提出两层间“最优滤管比”以研究坑内降水的最优方案，为类似复杂水文地质条件下深基坑降水提供针对性、目的性更强的参考依据。

1 工程实例分析

1.1 工程概况

某深基坑为荆州市修建某翻车机房所需基坑，场区全部位于陆域，地形较平坦，高程多在30 m左右，地表以农田为主，场区东侧60 m以外为已建成的铁路桥墩，其余区段外围100 m范围内无重要建(构)筑物，均为空地，临近荆江河岸北段。基坑周长为316 m，面积约为5 587.25 m，南北两侧基坑面积相当。基坑北侧区开挖深度较大，约为26.2 m；基坑南侧区开挖深度略小，约为19 m。该基坑平面布置如图1所示。

图1 某基坑平面示意图Fig.1 Schematic plan of a foundation pit

1.2 工程地质及水文地质条件

表1 某基坑土层分布及相关参数

拟建场地地下水类型主要为赋存于上部土层中的孔隙潜水以及中、下部砂性土组、卵砾石组中的承压水，即分别对应构成第一、二承压含水层。

孔隙潜水赋存于地表以下黏性土组覆盖层中，该类土孔隙度较小，渗透性较差，水量随季节变化，其主要接受大气降水补给，其次为下部富水层补给，排泄方式主要为蒸发，勘探期间测得孔隙潜水的水位为29.6～30.8 m。

弱承压水赋存于黏性土组覆盖层以下的地层中，主要的富水层为砂类土层及卵砾石层，该类土孔隙度较大，渗透性较好，水量随季节变化明显，其主要接受远源大气降水的侧向径流补给和长江水的侧向补给，向相邻含水层径流排泄，其次为人工抽水排泄,勘探期间测得孔隙承压水水位约为27.9～29.5 m。对该基坑开挖影响较大的地层涉及④、⑤粉细砂和⑥卵石层，勘探钻孔未揭露卵石层厚度，因此控制地下水成为基坑开挖的关键。

1.3 基坑承压水控制方案

1.3.1 单井试验

为了获取场区有效水文地质参数，分别在砂土层和卵石层中布置水文观测孔，其中砂土层试验采用1个抽水孔和3个观测孔，选取孔深范围为14.0～30.0 m作为抽水试验段；卵石层试验采用1个抽水井、2个观测井，选取孔深范围为30.0～35.0 m作为抽水试验段。抽水井为承压非完整井结构，累计抽水时间约为30 h，流量采取由小到大先后进行3次稳定流抽水试验，其试验结果见图2。

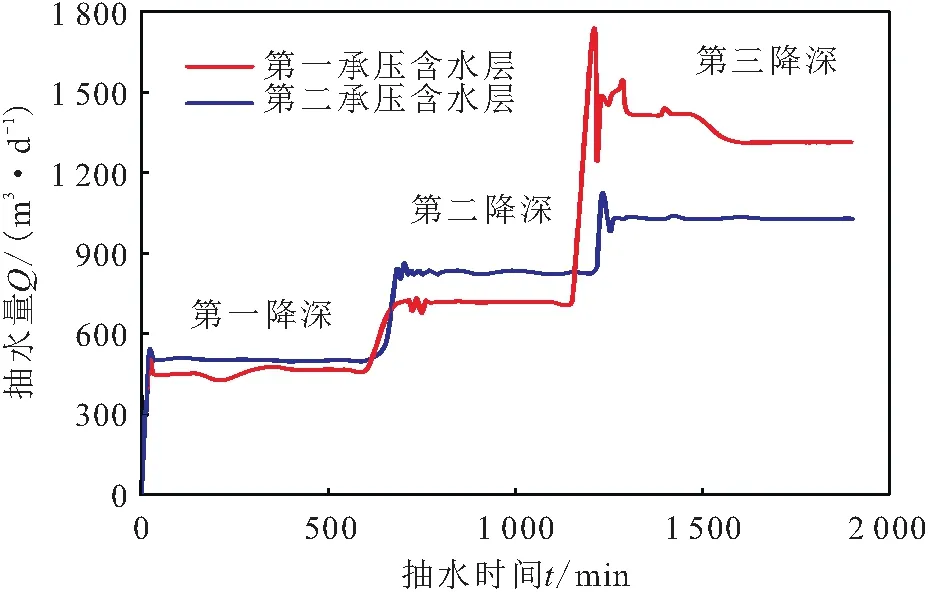
图2 单井试验Q-t变化曲线Fig.2 Cumulative pumping Q-t versus time curves of single well test

由图2可见，第一承压含水层累计单井抽水量≤1 400 m/d，第二承压含水层累计单井抽水量≤1 100 m/d，抽水约100 min时承压含水层水位基本稳定。

场区水文地质参数依照《水利水电工程钻孔抽水试验规程》(SL 320—2005)，承压含水层稳定流非完整井渗透系数

K

及影响半径

R

的计算结果如下：第一承压含水层：

K

=1.6×10cm/s，

R

=95.3 m；第二承压含水层：

K

=2.5×10cm/s，

R

=150.9 m。

1.3.2 基坑抗承压水突涌稳定性验算

为了防止高水头承压水由最不利点突涌从而造成基坑危害，根据《建筑基坑支护技术规程》(JGJ 120—2012)中附录C.0.1，对该基坑抗承压水突涌稳定性进行验算，其计算公式如下：

D

·

γ

≥

F

·

h

·

γ

(1)

式中：

γ

为坑底隔水土层平均重度(kN/m)；

D

为承压含水层顶面至坑底的土层厚度(m)；

F

为基坑抗承压水突涌稳定安全系数(取值为1.10)；

h

为承压水高度(m)；

γ

为水的重度(kN/m)。以北侧深坑抗承压水突涌稳定安全系数计算为例，第⑥层承压含水层顶标高为0.43 m，承压水头标高为29.5 m，坑底标高为4.2 m，

γ

取19.0 kN/m，按压力不平衡法，不采取降压措施时，北侧深坑抗承压水突涌稳定安全系数为0.25(<1.10)。同理，计算得到南侧浅坑抗承压水突涌稳定安全系数为0.73。即基坑整体的承压水压力远大于土压力，故需采取措施降低承压水头。

1.3.3 初步降水方案

针对基坑开挖深度涉及到的上、中、下含水层的补、径、排特征，提出的基坑地下水控制方案为：侧壁隔水帷幕+深井降水。

本基坑工程按照“封闭止水，按需降水”的原则，浅坑初步布置14口降水井(含2口备用降水井BG1、BG2)，其余12口井编号为J1-(J～J)，井深为27～35 m， 滤管长为6～14 m； 深坑初步布置17口降水井(含3口备用降水井BG3、BG4、BG5)，其余井的编号为J2-(J～J)，井深为38～40 m，滤管长为9～21 m。降水井与地层剖面相对位置关系见图3，图中(1)、(2)为深坑区降水井抽取卵石层中地下水，(3)、(4)为浅坑区降水井抽取砂土层中的地下水。

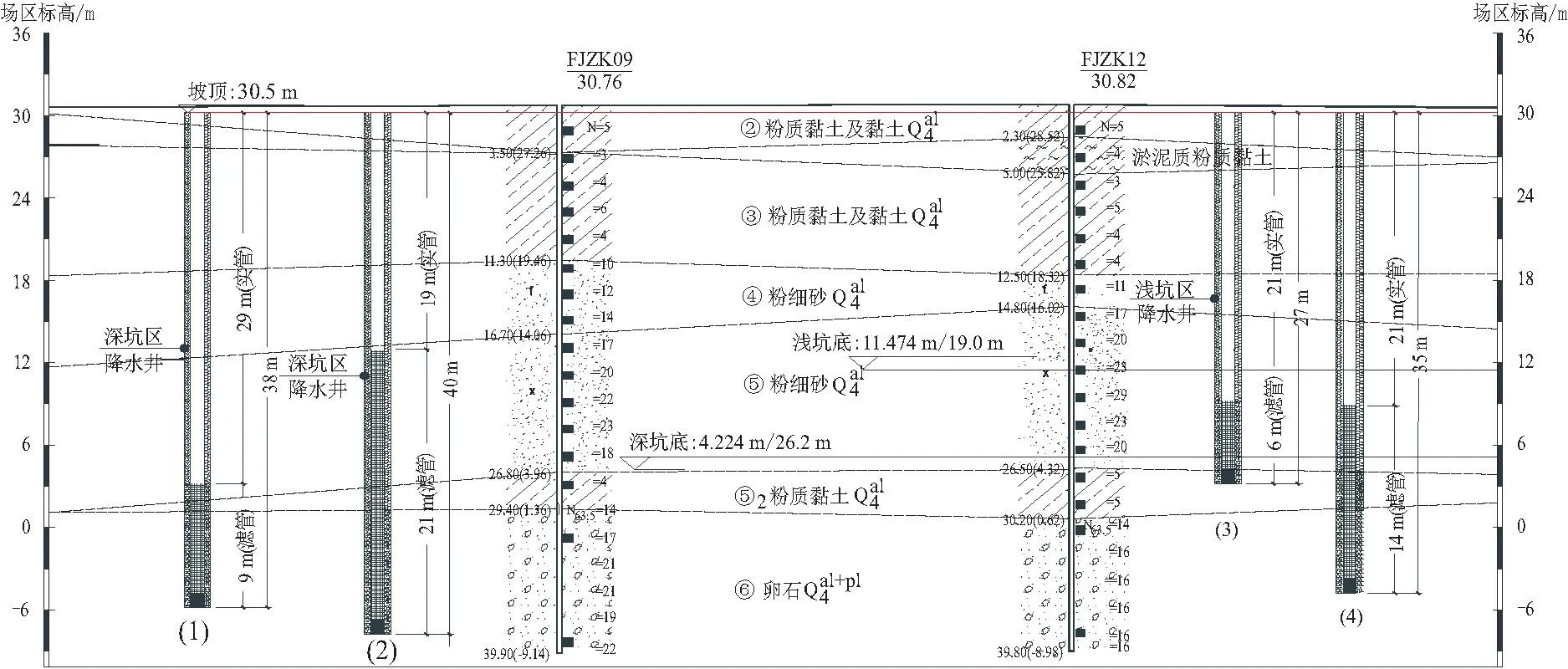
图3 降水井与地层剖面相对位置关系Fig.3 Relative position relationship between precipitation wells and stratigraphic sections

1.4 群井试验

为了验证实际降水效果，开展了深浅坑群井试验，降水井平面布置如图4所示。

图4 降水井平面布置图Fig.4 Layout of precipitation wells 注：蓝色标记(×)为暂时未抽水井，其余均为抽水井

试验前测得场区内孔隙承压水水位为26.9～27.8 m。整个试验选取20口井开启抽水，抽水井泵量为32～80 t/h，轮流选择1口井作为观测井。根据《基坑降水手册》，当最远观测孔水位波动值<2～3 cm时即达到稳定，本次试验观测井水位在停抽2 h后稳定，再开启本口观测井同时停抽下一口待测观测井，逐一循环完成深坑内所有井的静止水位观测，抽水累计时间约38 h。群井试验结果见表2。

表2 群井试验结果汇总

群井试验中，抽水可以有效降低承压水头，浅坑采用32 t/h小泵抽水，降水目标层为粉砂层，轮流观测观测井J1-水位变化，其水位有较灵敏的变化，基本满足浅坑坑底开挖要求(基底标高为11.4 m)；深坑采用80 t/h大泵抽水，降水目标层为卵石层，轮流观测观测井J2-水位变化，其水位变化幅度较小，较浅坑的降水效果差，而深、浅坑间面积仅差252.75 m，坑内、外降水均存在差异，说明卵石层补给水量大。

基于以上分析，初步方案未能实现承压水水位降至基底以下安全范围，后续将对其进一步优化，以达到最优降水效果。

2 多层承压含水层降水优化研究

为了研究最适宜本基坑工程深井结构的优化值，本次采用承压非完整井理论并结合数值模拟软件Visual Modflow，针对承压不完整井滤管结构参数(滤管数量、长度、位置)的设定进行讨论，分析多种滤管结构的优化结果，提出适宜本基坑工程深井结构的建议。

2.1 承压非完整井理论基础

沙金煊提出将渗流场以假想的虚线分开，分为上、下部渗流场，求得流线长度加权平均，运用井附近的局部抗阻概念，将不完整井的轴向渗流场以

r

+

ξT

为界，分为内圈急变区和外圈缓变区两个渗流场(见图5)，运用流量连续原理得到井流量的计算公式如下：

(2)

(3)

式中：

Q

为井流量(m/d)；

K

为土层渗透系数(m/d)；

h

、

H

分别为井口、井轴

R

处的水头(m)；

f

为不完整井附近流线急剧弯曲产生的附加阻力；

s

为滤管长度(m)；

T

为透水层非滤管部分的厚度(m)。

图5 滤管顶位于含水层层面的计算模型Fig.5 Calculation model of the filter tube at the aquifer level

若采用普通井可使用上述计算模型，但本基坑工程为多层含水层，也可采用混合井双滤管结构，同样分上、下渗流场，可参考曹洪等的做法采用等比例分配法进行改进，将该计算模型进行简化(见图6)，假设上下两层渗流路径相同、井滤管长度与其含水层厚度比值相等、不考虑越流等复杂情况，从而得到两个附加阻力并求得井流量，具体计算公式如下：

s

/

T

=

s

/

T

=

s

/

T

=

a

(4)

(5)

井的总流量为上、下部渗流场井流量之和：

Q

=

Q

+

Q

(6)

根据上述方程，若

T

、

T

、

H

、

h

、

R

、

R

、

r

、

K

、

K

已知，当控制混合井双滤管总长度为

s

时，含水层上部滤管长度为

s

，则含水层下部滤管长度

s

=

s

-

s

。结合多层含水层水文地质条件，因上部含水层滤管长度

s

未知，故本次借助数值模拟软件进行解析解的计算。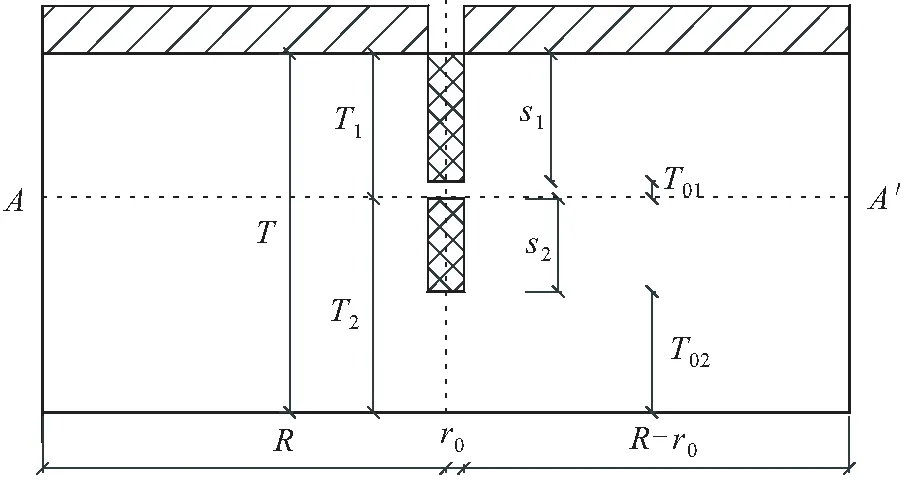

图6 本算例计算模型Fig.6 Calculation model for this study

2.2 承压非完整井数值模拟

根据本基坑工程特点，对计算模型作出如下假设:

(1) 土层渗透系数为某一定值，且各向同性；

(2) 土层中地下水渗流运动遵循达西定律。

地下水渗流模拟中的影响半径

R

=150.9 m，水平方向有限元计算域以基坑的东、西、南、北最远边界为起点，各向外扩展200 m，即计算区域设为600 m×500 m。为了保证计算精度，对基坑内管井密布区进行网格细化，每个单元的水平尺寸为2 m×2 m，随着计算范围与基坑距离的增加，逐渐放宽单元格，见图7。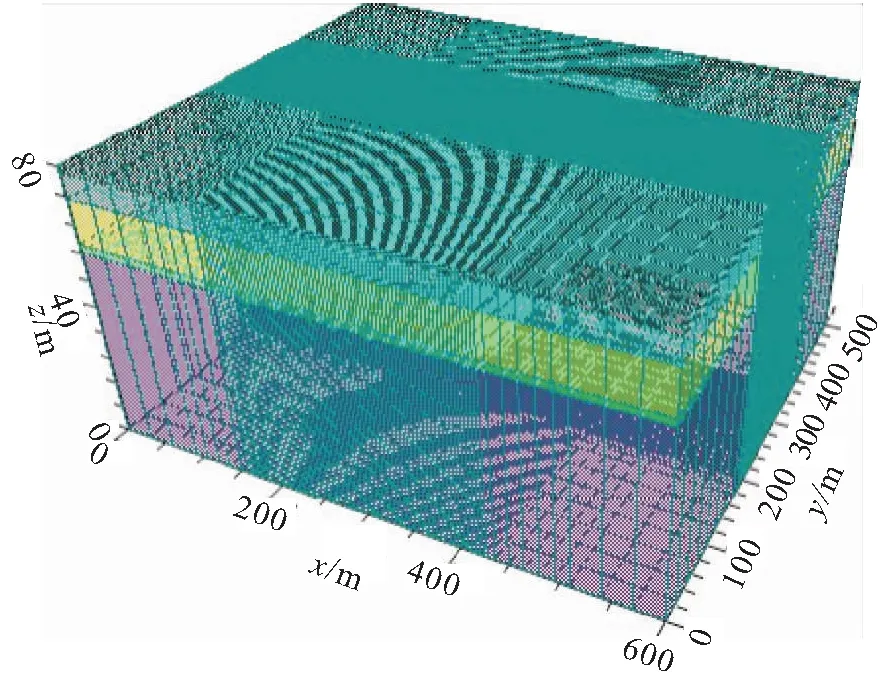

图7 计算模型三维示意图Fig.7 3D model of the calculation model

由于场地范围相对较小，地层起伏变化对模拟结果的影响较小，故为了节约建模及计算时间，将各土层概化为等厚度。根据模型取地面标高为30.5 m，从上到下将各土层概化为5个地层，经验证每层地层参数见表3，利用该模型能够较好地拟合现场观测井水位降深数据(见图8)，基本符合实际情况，便于进一步优化。

表3 地层数值模拟参数表

图8 观测井水位降深-时间拟合曲线Fig.8 Fitted curve of the water level drawdown of the observation well with time

为了克服由于边界的不确定性给计算结果带来的随意性，设置的定水头边界应远离源汇项，模型四周按定水头边界处理；初始水头第一、二承压含水层相同，设为地下-1 m(绝对标高为29.5 m)；止水帷幕采用墙边界(WALL)进行模拟，厚度设置为1 m，插入深度为28 m，渗透系数设置为1×10cm/s；深井27口，每口井设定抽水泵量为80 t/h，单井出水量为1 920 m/d。

2.3 混合井双滤管结构深井滤管数量的优化

本次对比了普通井单滤管和混合井双滤管的降水效果，以深坑为例，控制滤管总长度为21 m。普通井单滤管[标高为10～-11 m，见图9(a)]由第一承压含水层贯穿隔水层至第二承压含水层中，即构成“实管+滤管”的常规结构；另外一种结构为从地面向下交替布设实管与滤管，将降水井设计成集“疏干、减压”功能为一体的混合井，即开挖浅部土层时混合井起疏干作用，开挖中部及深部土层时起减压作用[见图9(b)]，混合井双滤管贯穿第一承压含水层10 m(标高18.5～8.5 m)、第二承压含水层11 m(标高为1.5～-9.5 m)。

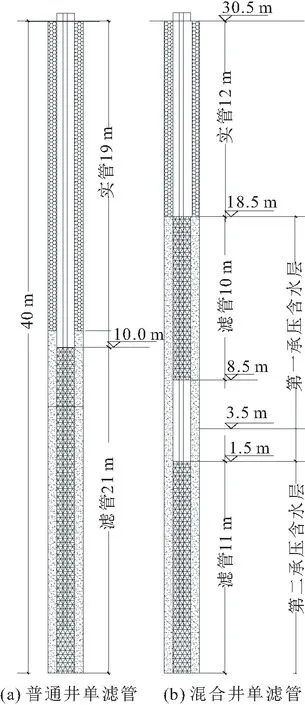
图9 滤管结构示意图Fig.9 Schematic diagram of the filter structure

同时开启双滤管混合井和单滤管普通井双模型，每口井设定抽水泵量为80 t/h，开启所有降水井，抽水天数设定为1 d、5 d、10 d、20 d，对比了抽水10 d、20 d后混合井和普通井第二承压含水层水位降深结果，见图10和图11。

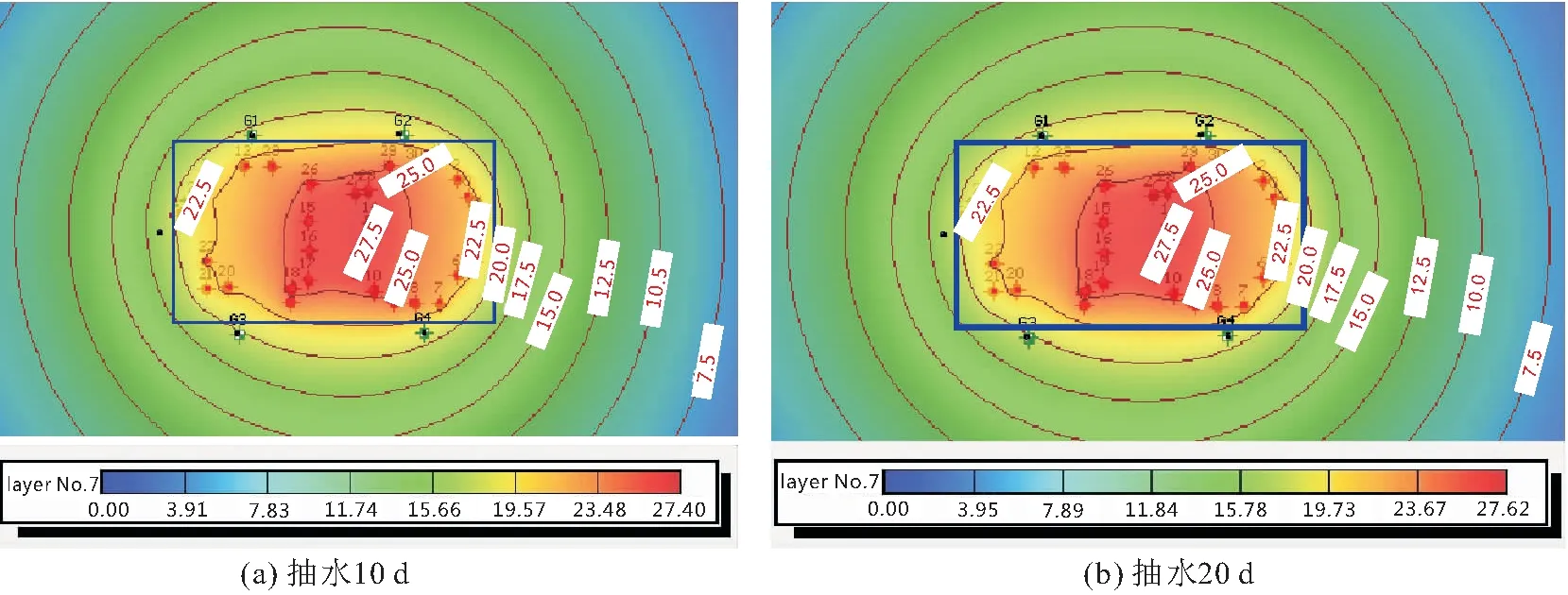
图10 混合井第二承压含水层水位降深云图Fig.10 Cloud chart of drawdown of the mixed well in the second confined aquifer

图11 普通井第二承压含水层水位降深云图Fig.11 Cloud chart of drawdown of the ordinary well in the second confined aquifer

由图10和图11可见，普通井单滤管结构坑内水位降深均小于混合井双滤管结构，普通井抽水10 d的水位降深最大为22.6 m，此时承压水头为6.9 m，高于基底开挖4.2 m，不满足深坑开挖要求；混合井承压水头达27.4 m，满足深坑开挖要求，故针对本基坑工程建议选用混合井双滤管结构。分析如下：当降水井不抽水时，上层滞水可缓慢渗透到混合井中并汇至承压含水层，起蓄水作用；当蓄水达到一定量进行降水抽水时，因两层承压水水头差，井流呈“窜流”状态，井管周围的承压水会以“爆发式喷射”方式透过滤网进入到降水井管内，井管内动水位在短时间内会急剧下降可使混合井中水位迅速降低，从而导致井内水位降低。

2.4 混合井双滤管结构深井滤管位于层顶时分层插入深度的优化

混合井滤管总长度同上为21 m，滤管位置由第一承压含水层层顶(标高为18.5 m)开始以1 m为步长渐变至层底，第二承压含水层滤管插入深度依次递减，共计15 种工况，见图12。本试验模拟得到混合井滤管长度与水位降深的关系曲线，见图13。

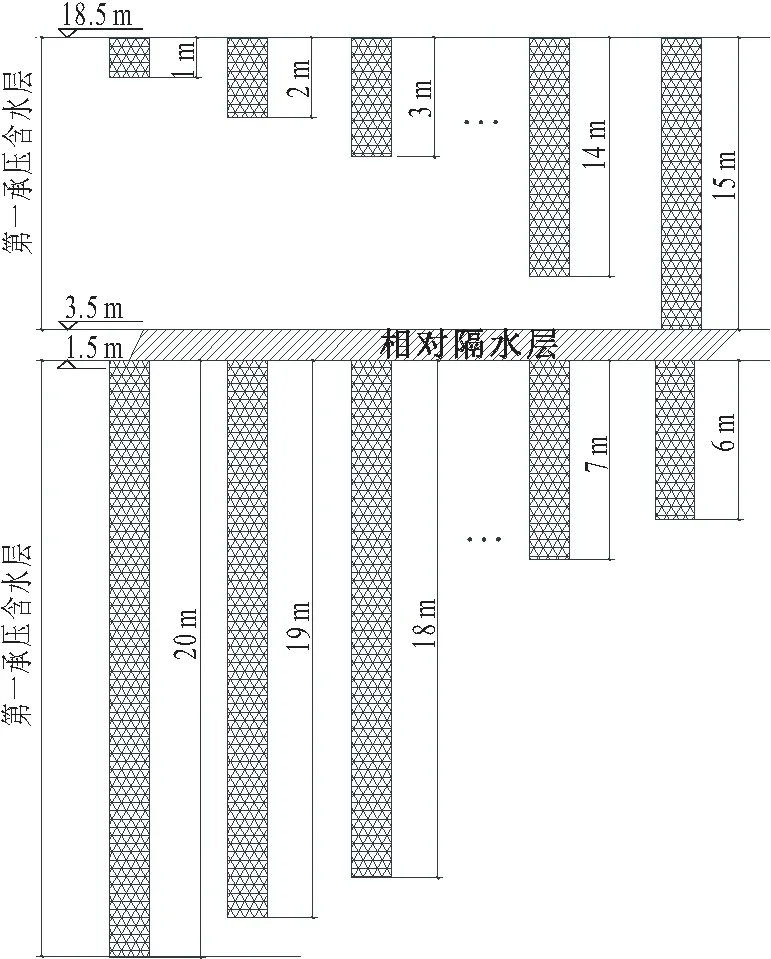
图12 混合井滤管长度示意图Fig.12 Schematic diagram of the filter length of the mixed well

由图13可见，随着混合井滤管位置由第一承压含水层层顶依次向层底移动，卵石层坑内水位降深逐渐变小，变化趋势较为平稳；当上部滤管(管底标高为3.5 m)完全贯穿第一承压含水层时水位降深最小为22 m。由此可见，地下水向管井运动具有分带特征，并非滤管越长水位降深越大；砂土层坑内水位降深先增大后减小，当上部滤管接近第一承压含水层层底时发生骤减；基坑坑外水位降深随着上部滤管插入深度的增长先减小，当上部滤管长度达10 m时(滤管底标高为8.5 m)开始增大，接近层底时逐渐减小。

图13 混合井滤管长度与水位降深的关系曲线Fig.13 Relationship between the filter length of the mixed well and the water level drawdown

依据实测和模拟结果，滤管总长21 m均满足基坑降水要求，建议降水井上部滤管应尽量靠近第一承压含水层中部，即上部滤管深入第一承压含水层10 m，深度约占第一承压含水层总厚度的2/3，上下分层滤管长度比为10∶11(约等于1∶1时)时达到最优值(即“最优滤管比”)，此时坑外水位降深最小，坑内降水效果明显。

2.5 混合井双滤管结构深井滤管空间分布位置的优化

由上述建议值进一步研究深井滤管的空间分布位置。因现场实际第二承压含水层深度未知，本次研究对象取上部滤管深入第一承压含水层10 m为定值，划分为3种：上部滤管位于顶部2/3处、上部滤管位于底部2/3处和上部滤管位于中部2/3处，见图14。本试验模拟得到的降水井滤管位置不同时的水位降深值，见表4。

图14 深井滤管空间位置分布示意图Fig.14 Spatial distribution of filter tubes in deep wells

由表4可见，将深井滤管空间分布位置划分为3种对坑内、外水位降深的影响很小，其中滤管(16.0～6.0 m)靠近第一承压含水层中部的井流量大于另外两种。分析原因如下：滤管顶或底端为不透水界面阻隔，井端进水量占井总流量的比例小，同样滤管长度，流线会随滤管位置的变化而改变，流线越短，阻力越小，过水断面面积越大，流量越大；但3种滤管位置的涌水量的差值较小，综合考虑建议降水井滤管应尽量靠近第一承压含水层层顶位置。

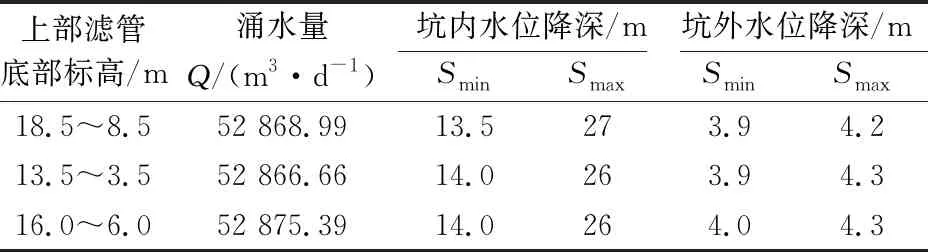
表4 降水井滤管位置不同时的水位降深值

2.6 理论计算结果与数值模拟结果的对比

为了验证上述优化值的可靠性，参考模拟结果，当采用混合井双滤管结构时，第一承压含水层参数为：

T

=15 m，

R

=95 m，

r

=0.14 m，

K

=14.39 m/d，

H

=30.8 m，

h

=29.5 m，

s

取1 m，2 m,…,15 m；第二承压含水层参数为：

T

=50 m，

R

=150 m，

r

=0.14 m，

K

=21.60 m/d，

s

=(21-

s

) m，水头取值相同，代入公式(6)可计算得到井的总流量理论计算值。并将井的总流量理论计算值与数值模拟结果进行对比，其相对误差见图15。

图15 理论计算结果与数值模拟结果的对比Fig.15 Comparison of theoretical calculation values and simulation values注：相对误差(%)=(理论值-模拟值)/模拟值×100%

分析可得：①经计算，当

s

/

s

=10/11=0.91≈1时精度最高，此时单井

Q

=503.4 m/d、

Q

=1 321.26 m/d，与模拟相匹配，设置27口井，井的总流量

Q

=49 265.8 m/d，相对误差值仅为6.81%，与模拟结果基本相符；②两种计算方法整体计算结果的吻合度较高，最大相对误差约为12%，进一步增强了优化措施的可信度。

3 优化后的降水方案与验证

3.1 优化后的降水方案

根据现场降水效果，结合理论与模拟计算结果，优化后的降水方案如下：浅坑布置降水井14口(井深为27～35 m)，深坑布置降水井27口(井深为38～40 m)，均深入第二承压含水层，共计41口降水井，其中混合井19口。配置水泵功率为32～100 t/h，基坑外侧布置6口观测井，以检查止水帷幕的效果。考虑到工程地质勘察不能完全揭示地层局部的差异以及止水帷幕可能存在渗漏等因素，需在坑内预留备用井，以备在突发情况下兼降水井使用。

3.2 降水效果验证及现场监测

在降水过程中务必做到“按需降水”，随基坑开挖深度的逐渐加大，需逐步开启更多的降水井来降低承压水头，经统计选取深、浅坑内观测井的地下水水头平均值，见图16。

图16 基坑地下水水位变化曲线Fig.16 Variation curves of groundwater level in the foundation pit

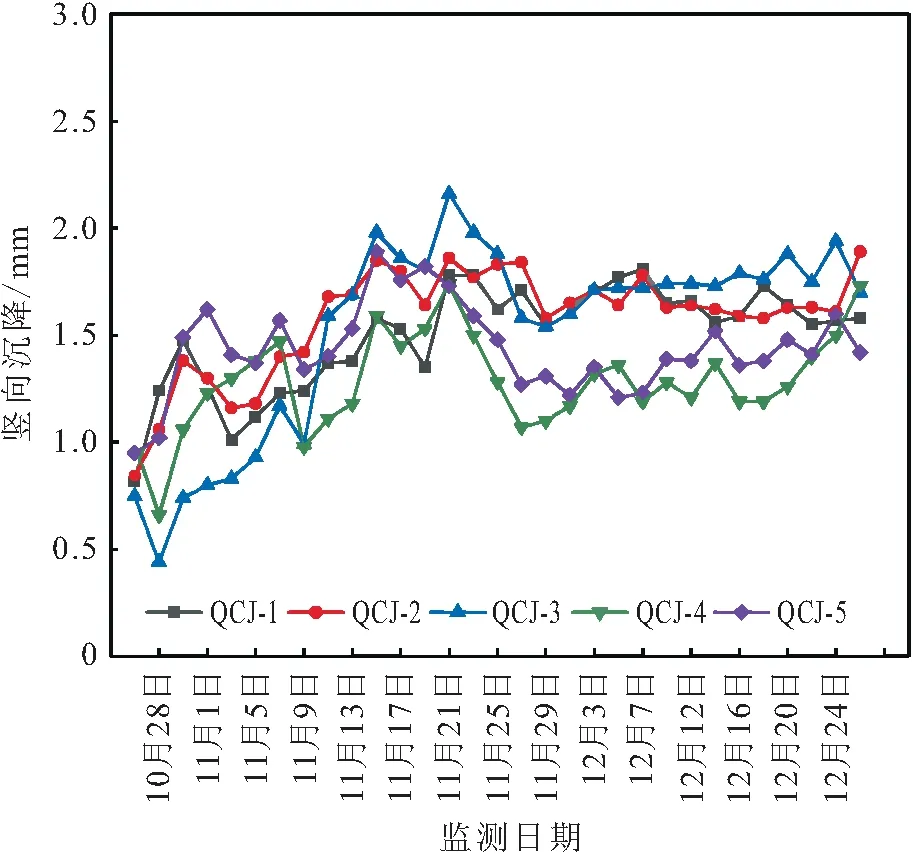
图17 基坑附近铁路桥墩竖向沉降的监测曲线Fig.17 Monitoring curves of vertical settlement of the railway bridge pier near the foundation pit

当采用混合井降水后，浅坑区域承压水头基本满足基底开挖要求，深坑地下水水位降幅明显增大，最终稳定地下水水位标高约为5.7 m，距离深坑底板安全水位不足2 m，后期持续抽水结合明排方法可保证地下水水位降至底板以下。

降水的同时务必监测其对周边环境的影响，结合布设在基坑临近铁路桥墩的5个监测点(见图1)的实测结果(见图17)，监测周期为60 d，结果显示：竖向沉降最大点为QCJ3，其最大值为2.16 mm，在规范允许的范围内，说明整个降水工程的方案设计及施工管理较合理，基坑降水未对临近铁路桥墩造成不良的影响。

4 结 论

本文针对多层承压含水层中深基坑减压降水措施进行了讨论，降压时采用混合井双滤管结构的降水效果明显，得出如下结论：

(1) 该基坑工程处于多层承压含水层的复杂水文地质条件下，在基坑降水设计与施工中应慎重对待中、下部高承压水头的处置，布设在下部强透水层中的降水井深度要适当，并非滤管插入越深降水效果越好。

(2) 该基坑工程前期降水效果不佳，优化后采用混合井替代部分疏干井与减压井，其降水效果明显，避免了常规深井降水中同时在浅部潜水层设置疏干井、在深部承压水层设置减压井的冗繁施工。相同开启数量的混合井与普通井对比，混合井设计时的水位降深满足深坑底板开挖要求，较好地适应场地内各分项施工对降水的需求。

(3) 在本基坑工程中，因下部卵石层未见底，本次以第一承压含水层滤管插入深度为控制变量，结合有限元分析并套用沙金煊公式，提出该基坑工程上下分层滤管长度的最优比值约为1∶1，即上部滤管位于第一承压含水层的长度与下部滤管位于第二承压含水层的长度相当；滤管插入深度建议取第一承压含水层厚度的2/3，即从第一承压含水层层顶向下10 m，此时可达到最优降水效果。