地铁深基坑内支撑结构优化分析
2021-03-11贺振昭李忠超梁荣柱蔡兵华肖铭钊吴文兵
贺振昭,杨 新,叶 超,李忠超,梁荣柱,5,蔡兵华,肖铭钊,吴文兵,5
(1.中国地质大学(武汉) 工程学院,湖北 武汉 430074;2.武汉城建集团,湖北 武汉 430022;3.武汉市市政建设集团有限公司,湖北 武汉 430023;4.武汉大学土木建筑工程学院,湖北 武汉 430072;5.广西大学土木建筑工程学院,广西 南宁 530004)
深基坑工程中有关围护结构的稳定性、变形规律、经济性等问题一直是研究的热点。最早Peck通过对深基坑开挖变形计算理论进行了细致的研究,最先提出了预估深基坑开挖稳定和支撑内力的总应力法;O’Rourke通过分析基坑开挖及相关工程活动引起的土体变形,指出基坑开挖前期的工程活动如降水、围护结构施工、桩基施工等会对土体的变形产生影响,并讨论了支撑刚度、支撑加预应力、最下道支撑以下的开挖深度、预留土的作用等对基坑变形的影响;Long通过搜集大量的监测数据,指出基坑开挖深度、支撑刚度等对基坑变形有较大的影响;曾国熙等、应宏伟通过比较不同支撑、挡墙刚度、开挖方式和土的力学性质等对土体沉降的影响,分析了支护结构、基坑形状、土体固结等因素对土体沉降的影响;李云安等探讨了影响基坑变形的主要因素,认为围护结构刚度、入土深度、支撑刚度和道数、预应力、土体变形模量这6个因素对基坑变形的影响较为显著。
国内外学者对深基坑开挖变形规律及对周边环境的影响等方面做了大量的研究,对优化基坑工程设计和施工具有重要的作用。但基坑的支护形式是影响基坑变形的重要因素之一。深基坑的支护结构和形式多样,目前在深基坑支护结构中比较常用的是桩墙+内支撑的支护形式,常见的支护形式有排桩+内支撑、地连墙+内支撑、桩锚+内支撑等,内支撑一般分为钢筋混凝土支撑与钢支撑两种类型。Clough首次将有限单元法运用到基坑工程分析中,使数值分析方法在挡土结构分析中得到了广泛应用;Potts等采用数值分析的方法分析了两种内支撑类型的受力和变形特征;彭社琴结合润扬长江公路大桥南汊北锚碇超深基坑工程实例,利用三维数值模拟技术对其支护结构进行了拟合分析,将墙体厚度、支撑间距、支撑刚度作为可变因素考虑,指出支护结构体系刚度决定基坑支护结构是否足够安全;何璠对基坑开挖过程中的不同工况进行了有限差分数值模拟分析,通过采用单因素控制变量的分析方法,在不同围护桩刚度、钢支撑刚度以及不同水平支撑间距等变量的模拟分析中,总结了基坑围护结构水平位移以及基坑周围地表沉降的相关规律。Tan等结合上海某基坑工程失稳案例,分析了该基坑前后两种支护结构设计方案,指出不同支护结构设计方案对围护结构系统刚度的影响较大;王卫东等利用Plaxis 3D有限元软件对上海地区板式支护体系基坑开挖进行了计算,并对结果进行归一化处理,考虑了系统刚度对基坑开挖变形的影响。
综上研究可知,前人已从围护结构刚度、支撑数量和间距以及开挖方式等方面研究了影响深基坑开挖的影响因素,而在基坑设计中加减基坑支撑数量对基坑整体稳定性具有至关重要的影响。相对而言,我国上海、台北、长沙等地区含黏土层的基坑内支撑结构优化研究较为丰富,而现阶段武汉市有关地铁基坑内支撑结构设计的工程实例较少,可借鉴的经验较少。而本项目基坑开挖深度达26.9 m,所在的长江Ⅰ级阶地含较厚细砂层,是武汉市典型的深基坑工程案例,能为存在较厚细砂地层的类似深基坑工程变形范围研究提供参考。为此,本文以武汉市某地铁深基坑工程项目为依托,首先为该地铁深基坑工程项目提供施工前期数值模拟变形预测以及设计建议;然后对该工程项目部所提出的两种基坑支护结构设计方案进行变形安全分析,为施工设计提供合理的优化建议;最后针对数值模拟中地层与结构的参数选取是否准确加以验证,即将施工后所得的真实变形数据与前期模拟结果进行对比来反证数值模拟结果的正确性。该研究结果可为武汉地区类似基坑工程项目提供借鉴。
1 某地铁深基坑工程概况与设计方案
1.1 基坑工程概况
本项目基坑工程设计尺寸长为176.8 m,标准段外包宽度为23.5 m,盾构端外包宽度为29 m,基坑标准段开挖深度为26.5 m,盾构工作井开挖深度为27.9 m,基坑开挖总面积达4 288.2 m,距离长江仅3 km。图1为武汉市某地铁深基坑工程平面示意图,其中基坑东、西两侧均存在堆土区,且施工期间无法清除。
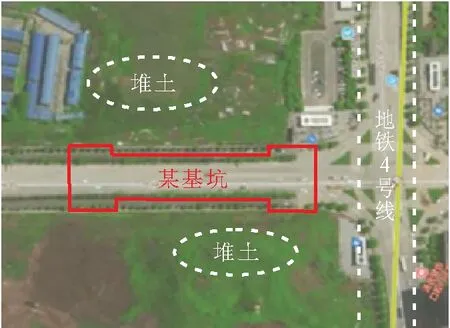
图1 武汉市某地铁深基坑工程平面示意图Fig.1 Diagram of the plane plan of a subway deep excavation project in Wuhan City
由前期勘察情况可知,该基坑施工场地地形平坦,地势起伏不大,属长江冲积Ⅰ级阶地,具有明显的二元结构特征。该基坑由上而下主要地层分布为:素填土、粉质黏土、淤泥质粉质黏土、粉质黏土夹粉土、粉砂、粉细砂、中粗砂夹砾卵石、强风化砂砾岩、中风化泥质粉砂岩。表1为该地铁深基坑各层土体物理力学参数。基坑部分开挖深度位于砂层,在施工过程中为了避免基坑渗水和突涌,设计了嵌岩式地下连续墙作为止水帷幕,同时在基坑内外采用“深井降水”的方式进行降压处理。评定此项目为一级超深基坑工程,施工过程中对围护结构的变形控制要求较高。
1.2 基坑支护结构设计方案
该地铁深基坑工程项目部提出了2种基坑支护结构设计方案(见图2),均采用相同地下连续墙(简称地连墙)设计,厚度为1 200 mm,墙深约45 m,墙体嵌入中风化泥质粉砂岩不少于1 m,地连墙顶浇筑冠梁一圈。基坑具体的支护结构方案设计如下。
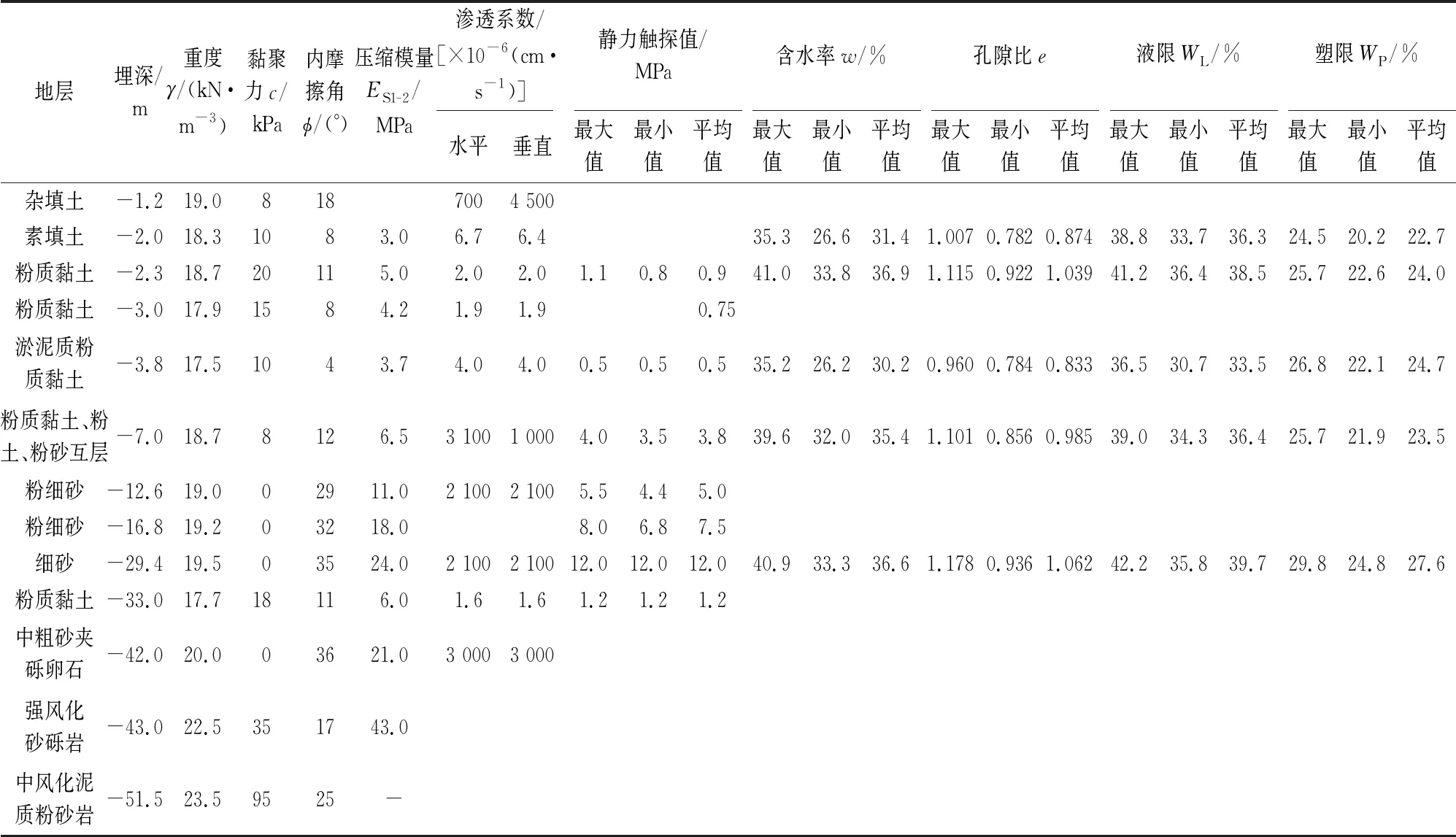
表1 某地铁深基坑各层土体物理力学参数
(1) 方案一:采用3道混凝土支撑和2道钢支撑,基坑支护结构剖面图如图2(a)所示。内支撑中第一道、第三道和第四道内支撑采用钢筋混凝土支撑,各支撑间的水平间距为6 m,支撑截面尺寸分别为1 000 mm×800 mm、1 200 mm×1 000 mm和1 200 mm×1 000 mm;第二道和第五道内支撑采用直径为800 mm、壁厚为20 mm、钢材为Q235钢管支撑作为内支撑体系,钢管之间的水平间距均为3 m。基坑具体的开挖工况如下:
工况一:开挖至2.1 m处浇筑第一道混凝土支撑;
工况二:开挖至8.9 m处安装第二道钢管支撑,并施加预应力;
工况三:开挖至13.7 m处浇筑第三道混凝土支撑;
工况四:开挖至18.7 m处浇筑第四道混凝土支撑;

图2 某地铁深基坑标准断面支护结构剖面图Fig.2 Section of standard section supporting structure of a subway deep excavation
工况五:开挖至23.9 m处安装第五道钢管支撑;
工况六:开挖至26.9 m处到达设计基坑深度。
(2) 方案二:采用3道混凝土支撑和3道钢支撑,基坑支护结构剖面图如图2(b)所示。内支撑中第一道、第四道和第五道内支撑采用钢筋混凝土支撑,支撑截面尺寸分别为1 000 mm×800 mm、1 200 mm×1 000 mm和1 200 mm×1 000 mm;第二道、第三道和第六道内支撑采用钢管支撑,各支撑间的水平间距均与方案一相同。基坑具体的开挖工况如下:
工况一:开挖至2.1 m处浇筑第一道混凝土支撑;
工况二:开挖至7.9 m处安装第二道钢管支撑,并施加预应力;
工况三:开挖至11.8 m处安装第二道钢管支撑,并施加预应力;
工况四:开挖至14.4 m处浇筑第三道混凝土支撑;
工况五:开挖至18.5 m处浇筑第四道混凝土支撑;
工况六:开挖至23.0 m处安装第五道钢管支撑;
工况七:开挖至26.9 m处到达设计基坑深度。
2 基坑有限元模型建立与测点布置
2.1 建立有限元模型与参数设定
Plaxis 3D是一款在岩土工程中应用广泛的有限元数值模拟软件,并且率先引入了土体硬化模型(HS模型)和小应变土体硬化模型(HSS模型),这种土体本构模型能够考虑到土体的受荷历史和刚度变化与应变率的相关性。Ou等运用Plaxis 3D中的HS模型来模拟基坑开挖,结果表明数值模拟结果与实际情况较为符合。
首先,建立大小尺寸为530 m×220 m ×70 m的有限元模型,基坑尺寸与实际的比例设计为1∶1。然后,设定模型底部边界竖向位移以及四周侧壁水平位移均为零,即地表荷载作用下边界处不产生变形,且计算边界远大于基坑开挖预计影响范围,以降低边界效应对计算结果的影响。由于基坑使用的是深入基岩的止水帷幕地连墙,基岩是天然的隔水层,在数值模拟中将地连墙设定为不透水后,即阻断了基坑内外地下水的流通,再对基坑内进行降水开挖模拟。将基坑场地东西侧堆土荷载分别简化为120 kPa和90 kPa的均布荷载。为了更好地反映土体剪切硬化和压缩硬化,土体本构模型采用能考虑小应变刚度的HSS模型;岩体采用摩尔库伦模型,因其强度较高,且深度均在基坑底面以下,故设定岩体仅出现线弹性变形;选用板单元来模拟地连墙,混凝土支撑和钢支撑则分别选用梁和锚杆单元进行模拟,均设定弹性变形。最后,结合现场及室内的试验,计算模型中土体和结构参数的选取见表2。为方便计算,有限元模型中将真实土层进行简化后,得到具体的5种地层类型,包括填土层、粉质黏土层、粉细砂层、强风化砂砾岩层和中风化粉砂岩层。其中,将杂填土与素填土合为填土层,由于杂填土中多为建筑垃圾,因此填土层的计算参数选取素填土的物理力学指标;粉质黏土层则由粉质黏土层和淤泥质粉质黏土层合并,粉细砂层则由粉细砂层和细砂层合并,均选取其中相应的各土层的物理力学指标平均值进行换算;深部较薄的粉质黏土层则忽略不计。
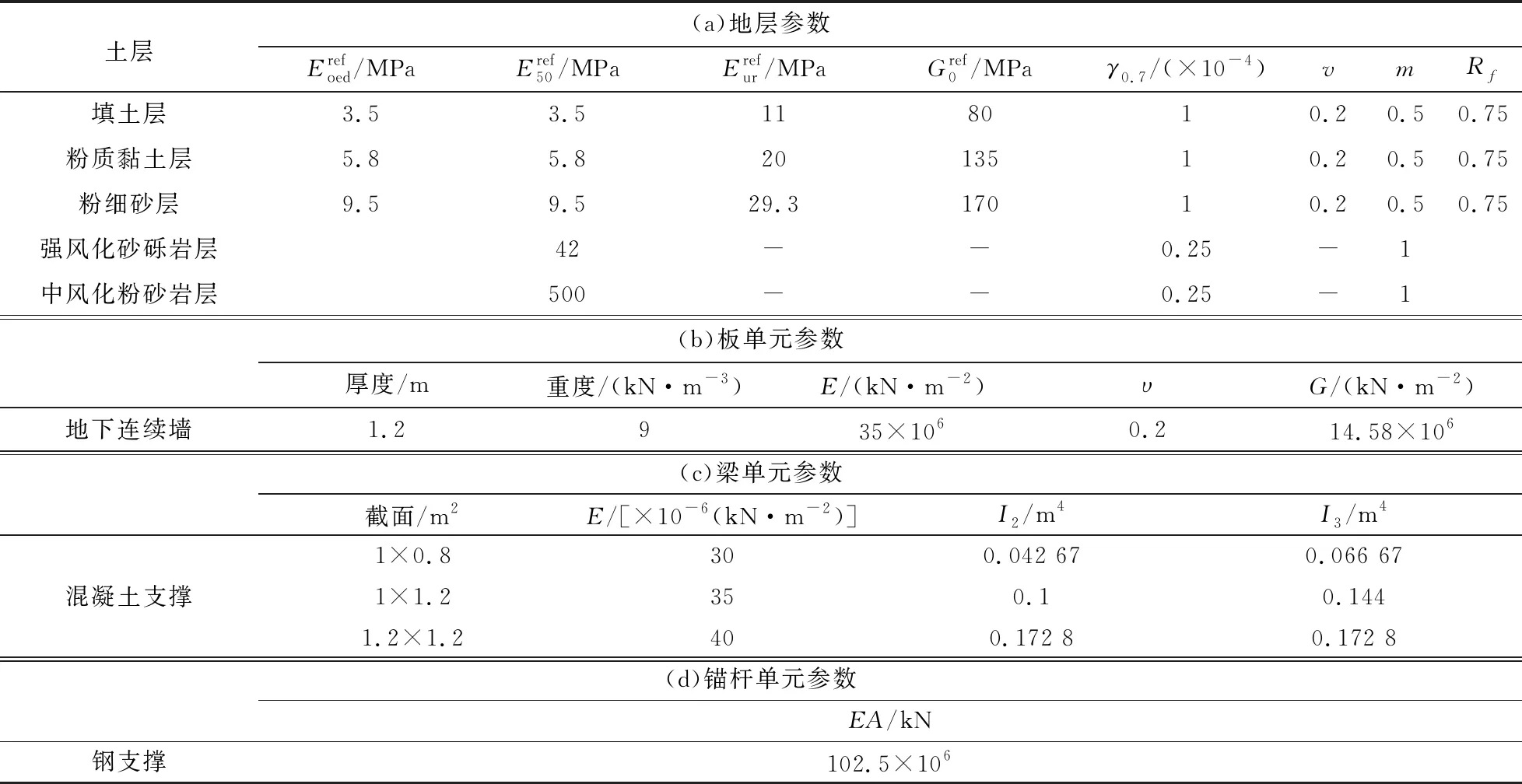
表2 有限元模型的计算参数
2.2 模型网格划分与测点布置
Plaxis 3D软件采取自动划分四面体土体单元的方式进行网格划分,选择单元密度为粗,图3为该基坑模型网格划分示意图,结果显示:方案一共生成21 966单元、36 630个节点;方案二共生成31 501个单元、50 441个节点。再设定基坑开挖施工步骤,采用K法进行初始应力计算,并设置在计算第一步开挖时将前期位移清零,计算后导出结果。图4为某地铁深基坑在两种支护结构设计方案下数值模拟计算得到的地连墙变形结果云图。

图3 某地铁深基坑有限元模型网格划分示意图Fig.3 Meshing diagram of a subway deep excavation model
由图4可见,该基坑在两种支护结构设计方案下地连墙沿y
轴方向的位移存在一定差异。为了细致地对比该基坑在两种支护结构设计方案下地连墙的变形情况,如图5所示,取基坑长短边的中点处作为数据提取点,即为B、C、L和R测点,同时由于基坑东西两侧存在较大面积的堆土,因此靠近两侧堆土的长边处分别取A和D测点提取基坑变形的计算结果,以便观察堆载对基坑变形的影响。
图4 基坑在两种支护结构设计方案下地下连续墙 变形结果云图Fig.4 Deformation nephogram of diaphragm wall under two supporting schemes
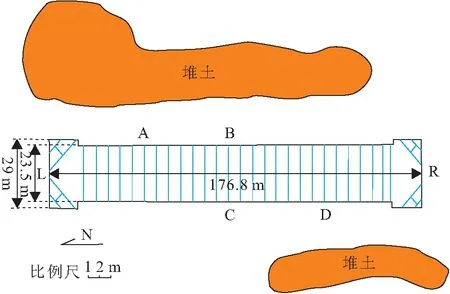
图5 某地铁深基坑平面测点布置Fig.5 Layout of monitoring points of a subway deep excavation
3 基坑有限元分析
3.1 基坑围护结构侧向变形模拟结果对比
图6为数值模拟得到的某地铁深基坑在两种支护结构设计方案下B和R测点处地连墙侧向变形随开挖深度的变化曲线。
由图6可见,该基坑在两种支护结构设计方案下地连墙侧向变形曲线除数值上有差异外,变形规律基本相同,墙体侧向水平位移曲线呈“弓形”模式,且墙体侧向水平位移随着开挖深度的增加而增大,同时其最大侧向水平位移发生的位置也随之下移,基本保持在开挖面附近。该有限元模拟得到的地连墙侧向变形曲线与前人所研究的基坑实际开挖地连墙侧向变形规律基本一致,表明数值模拟结果具有一定的可信度。
本项目基坑长边与短边的比值为6.1∶1,属于狭长型基坑,如图6所示,基坑长短边测点地连墙侧向变形的差异除基坑短边地连墙侧向变形数值较长边小以外,另一不同点在于A、B、C和D测点在基坑开挖至地表以下2.1 m时,地连墙最大侧向水平位移发生在墙顶,之后地表处地连墙侧向水平位移随着工况的进行而不断减小;L和R测点地表处地连墙侧向水平位移则随着工况的进行逐渐增大。其主要原因是基坑长边地连墙所受周边土体的约束较弱,且第一次开挖后无支撑结构,地连墙的侧向变形属于悬臂情况,因此地表处地连墙的侧向水平位移较大,随着开挖后各支撑的布设导致基坑长边整体强度得到提升,地表处地连墙侧向水平位移出现回弹现象。由于基坑角隅处结构刚度偏大,导致基坑短边地连墙侧向变形较小,且基坑短边支撑布设方式为斜撑,其对地表处土体的约束作用较长边的对撑形式弱,因此随着开挖深度的增大,地表处地连墙侧向水平位移呈不断增加的趋势。值得注意的是,图6中L和R测点处地连墙侧向变形曲线在坑底处出现明显的折线变化,其原因主要是坑角存在明显的空间效应,限制地连墙向坑内进一步变形的效果更显著,而基坑长边变形接近于平面应变条件,且所受约束较短边少,则坑底处地连墙侧向变形没有明显的突变情况。

表3 基坑在两种支护结构设计方案下B和R测点处地下连续墙的侧向变形数值模拟结果
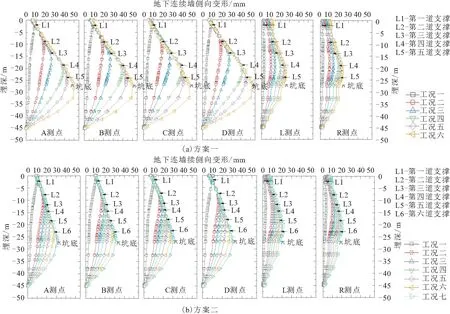
图6 基坑在两种支护结构设计方案下各测点地下连续墙侧向变形随开挖深度的变化曲线Fig.6 Lateral deformation curves of diaphragm wall at each measuring point with the change of excavation depth under two supporting schemes
由于篇幅所限,本文仅选取B和R测点来分析该基坑两种不同支护结构设计方案下地连墙侧向变形的特点,图7为该基坑在两种支护结构设计方案下B和R测点处各工况地连墙的侧向变形曲线。
由图7可见,采用方案二作为基坑支护结构时地连墙侧向变形的程度明显小于方案一;当开挖至基底时方案一下B测点的地连墙最大侧向水平位移为50.25 mm,而此时方案二下B测点处地连墙最大侧向水平位移为31.11 mm,位移减少约38.09%[见图7(a)];在开挖至基底时方案一和方案二下地连墙最大侧向水平位移分别为23.68 mm和19.68 mm,位移减少约16.89%[见图7(b)]。由此可见,基坑支护结构增加一道钢支撑后基坑长边地连墙最大侧向水平位移减小的幅度大于短边,但基坑短边最大侧向水平位移依然是小于长边。
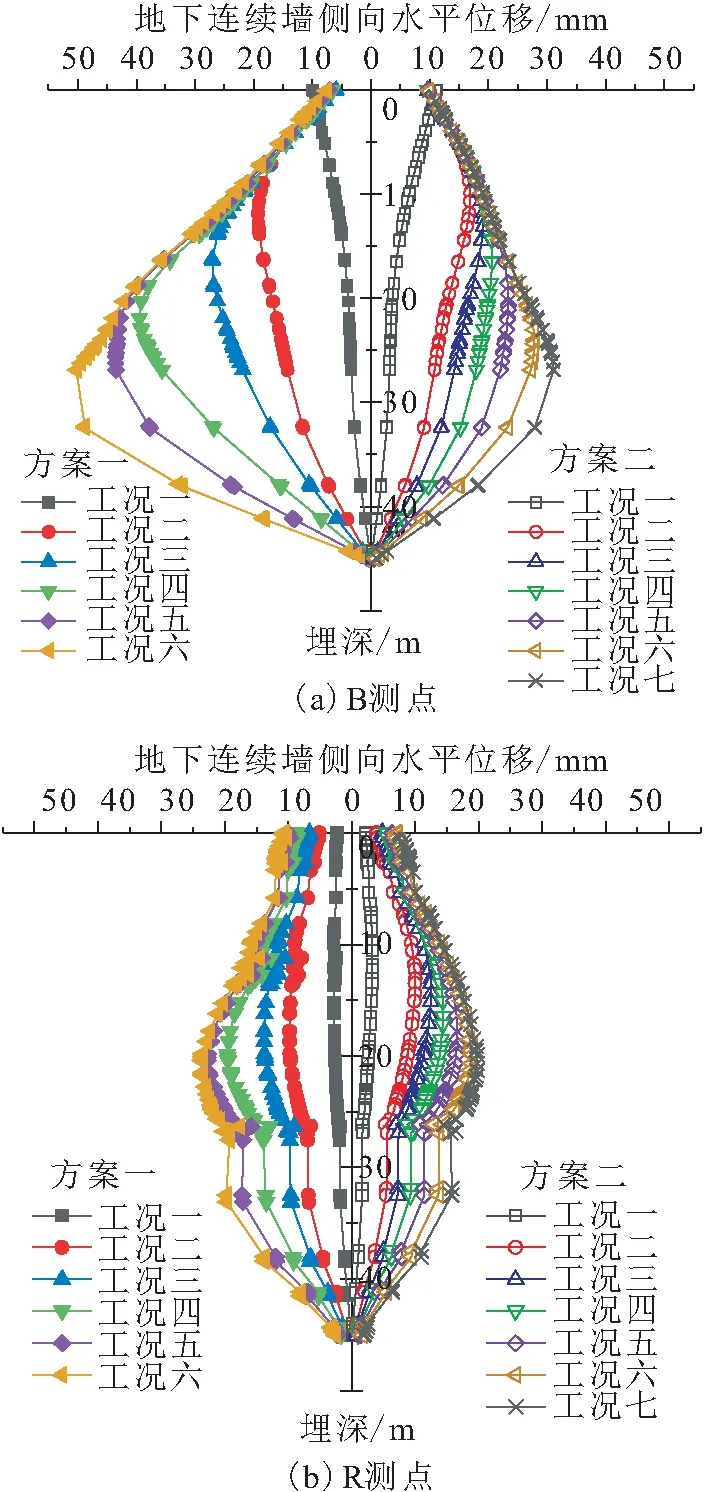
图7 基坑在两种支护结构设计方案下B和R测点处 各工况地下连续墙的侧向变形曲线Fig.7 Lateral deformation curves of diaphragm wall at measuring points B and R in two supporting schemes
同样以B和R测点为例,对比该基坑在两种支护结构设计方案下地连墙侧向水平位移数值的变化情况,表2为该基坑在两种支护结构设计方案下B和R测点处地连墙最大侧向水平位移以及每一工况位移的增幅结果。
由表2可知,该基坑在两种支护结构设计方案下工况一和工况二开挖深度相差较小,因此前两次开挖中同一工况两种支护方案下地连墙最大侧向水平位移之差不大于2.3 mm,且地连墙侧向变形曲线亦基本相同;相较于方案一,方案二在开挖至地表下11.8 m处多设有一道钢支撑,导致从工况二开挖至-14 m附近时,B测点处方案一下地连墙的侧向水平位移增幅达40.95%,而方案二增幅仅为22.22%。由于-14 m附近开挖至基底时,两种支护方案下支撑布置形式与位置基本相同,因此虽然相同开挖面附近方案一下地连墙的最大侧向水平位移均大于方案二,但在开挖至地表下19~26.9 m范围内,两种支护方案下地连墙的侧向水平位移增幅并没有明显差异,表明方案二中多加的一道钢撑对-11.8 m以下地连墙的侧向水平位移具有明显的限制作用,且导致地表以下约8~19 m范围内地连墙的侧向水平位移增幅显著减少。
3.2 Hm、δh与开挖深度H的关系分析
Ou等通过统计大量基坑现场监测数据后发现,基坑地连墙发生最大侧向变形的深度H
与当前开挖深度H
的比值接近1。图8为该基坑在两种支护结构设计方案下地连墙发生最大侧向水平位移的深度H
与当前开挖深度H
的关系曲线。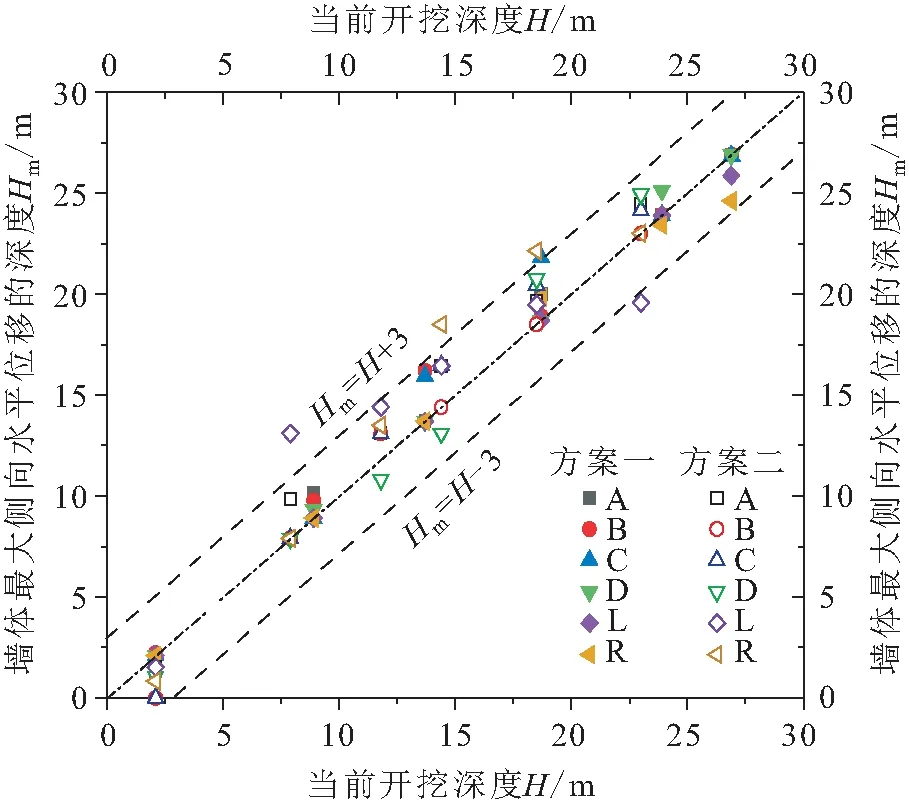
图8 基坑在两种支护结构设计方案下地下连续墙发生 最大侧向水平位移的深度Hm与当前开挖 深度H的关系曲线Fig.8 Relationship curves between maximum horizontal displacement depth Hm of diaphragm wall and current excavation depth H under two supporting schemes
由图8不难发现,方案一和方案二下地连墙发生最大侧向变形的深度H
均落在当前开挖深度H
为+3 m~-3 m的区间范围内,基本保持在开挖面位置附近,偶尔出现波动,表明基坑支护结构的改变对于地连墙发生最大侧向变形的深度H
并无较大的影响,同时两种支护方案下的模拟结果符合基本变形规律,进一步证实了模型设计的合理性和正确性。图9为数值模拟得到的该基坑在两种支护结构设计方案下地连墙最大侧向变形δ
与当前开挖深度H
的关系曲线。
图9 基坑在两种支护结构设计方案下地下连续墙 最大侧向水平位移δh与当前开挖深度H的 关系曲线Fig.9 Relationship curves between maximum horizontal displacement δh of diaphragm wall and current excavation depth H under two supporting schemes
由图9可见,方案一下墙体最大侧向水平位移δ
主要落在当前开挖深度H
为0.09%H
~0.21%H
的区间范围内,其中L和R测点侧向变形主要落在0.09%H
附近,而基坑长边上测点处墙体侧向水平位移点δ
主要落在0.17%H
~0.21%H
的区间范围内,基坑的空间效应导致墙体的侧向水平位移δ
的变化范围较大;方案二下墙体最大侧向水平位移δ
主要落在0.07%H
~0.14%H
的区间范围内,其范围略小于方案一,表明增加支撑数目使基坑系统刚度提高,能有效减少狭长基坑的空间效应。3.3 基坑系统支护体系刚度及设计方案选取
Rowe最早于1952年提出了柔度数概念,他基于原型及模型试验的位移并利用相似原理得出只适用于单支撑墙体的变形指标如下:

(1)
式中:E
为墙体的弹性模量(MPa);H
为墙体高度(m);I
为惯性距(m)。单支撑并不适用于复杂的内支撑情况,因此Clough等和O’Rourke研究指出,内支撑间距减小可大大提高基坑系统支护体系的刚度,并根据内支撑的数量和地连墙的刚度提出了基坑系统支护体系刚度K
的计算公式如下: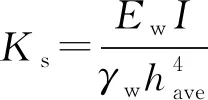
(2)
式中:E
I
为围护墙的水平抗弯刚度(MPa·m);γ
为水的重度(kN/m);h
为内支撑竖向平均间距(m)。之后,刘美麟等在Clough等基坑系统支护结构刚度的基础上,提出一种考虑围护墙、内支撑和墙后土体刚度的基坑支护体系综合刚度表达式,能用于正确预测基坑的变形量;徐洪钟等也在Clough等基坑系统支护体系综合刚度的基础上,在考虑围护结构、支撑体系与场地土层条件下,提出了改进的深基坑系统支护结构MSD综合刚度,用来反映不同地质条件下基坑系统支护结构的整体变形特性。由此表明,Clough等所提出的K
计算公式具有正确性,足以作为判定基坑系统支护体系刚度的基本标准。本项目中计算得到方案一的K
值为1 094(无量纲),而方案二的K
值为2 027(无量纲),仅从数值上判断,方案二因减少一道钢管支撑导致了基坑系统支护体系刚度下降了近一半。Liu等通过大量基坑实测数据统计分析指出,随着基坑系统支护体系刚度的下降将会引起墙体侧向水平位移的增加。类似地,上海某软土深基坑断面2开挖深度为16 m,原支护结构设计方案采用5道内支撑,而实际更改为4道内支撑,导致基坑存在超挖,最终致使墙体发生较大的变形。由此可见,在承压富水层加减基坑内支撑数量对基坑的安全性具有至关重要的影响,应慎重考虑。本项目中方案二因多一道钢支撑,支撑间的纵向距离最小仅为2.6 m,相对来说更不方便现场工人施工和仪器设备的操作。依据湖北省地方标准《基坑工程技术规程》(DB 42/T 159—2012)表4.0.7中当一级基坑周边无特殊重要保护对象,且与重点保护对象间的距离大于基坑开挖深度时,基坑支护结构水平变形应控制在50 mm以内。本次模拟结果中方案二的墙体侧向水平位移均小于35 mm,而方案一中基坑长边地连墙最大侧向水平位移均保持在40~50 mm左右,部分段墙体侧向水平位移略大于50 mm,总体上能满足规范对基坑支护结构的变形要求。尽管方案二基坑围护结构的刚度较大,墙体的最大侧向变形远远小于规范控制值,但是设计过于保守,会造成经济浪费,最终建议选取五道内支撑的支护结构设计方案进行基坑实际施工。
3.4 模拟结果与实测值的对比
本文选择与实际施工测斜监控点较为接近的C、D和R测点,对开挖至地表下23.9 m时地连墙侧向变形的有限元计算结果与实测值进行了对比,见图10。本次选取基坑开挖至地表下23.9 m工况进行对比的原因主要是此时开挖全断面进入了承压含水层,墙体新增侧向水平位移最大,更能反映有限元计算结果的合理性。

图10 基坑开挖至地表下23.9 m时地下连续墙侧向 变形模拟计算值与实测值的对比曲线Fig.10 Comparison curves between simulated and measured ateral deformation of diaphragm wall excavated at 23.9 m under the ground surface
由图10可见,3个测点处地连墙侧向变形曲线的模拟结果均大于实测值,但两者的基本变形规律一致;R测点模拟计算结果与实测数据两者地连墙侧向水平位移之差最大达15 mm左右,究其原因是:在实际施工中为了盾构机始发和接收安全,对基坑端部深层土体进行了深层搅拌桩加固,土体的强度得到了明显的提高,而前期有限元模拟中未考虑这一因素;D测点处地面以下20 m范围内模拟计算结果与实测数据两者地连墙侧向水平位移之差为10 mm左右,-20 m以下两者地连墙侧向水平位移之差甚微,基本保持一致,而C测点模拟计算结果与监测数据两者地连墙侧向水平位移之差在4~9 mm的范围内,显示模拟计算结果与实测数据具有较好的一致性,表明方案一作为基坑支护结构具有合理性,进一步证明有限元模型计算结果的正确性和可行性,有限元模拟能够反映基坑变形的一般规律,能为基坑支护结构的设计与施工提供参考。
4 结 论
本文以武汉市长江I级阶地富水砂层某地铁车站深基坑工程为依托,通过Plaxis 3D有限元软件对基坑开挖过程进行了有限元分析,得到主要结论如下:
(1) 在两种不同支护结构设计方案下,基坑地连墙侧向变形曲线基本呈“弓形”模式,墙体侧向水平位移均随着开挖深度的增加而增大,同时其最大侧向变形深度也逐渐下移,地连墙最大侧向变形位置基本保持在开挖面附近。
(2) 方案二中多加的一道钢支撑对-11.8 m以下地连墙侧向水平位移具有明显的限制作用,且导致地表以下约8~19 m范围内地连墙侧向水平位移增幅显著减少。
(3) 方案二因多一道钢支撑,基坑系统支护结构刚度为方案一的近2倍,因而地连墙的变形程度小于方案一,但其支撑间纵向距离最小仅为2.6 m,且方案一下地连墙侧向水平位移基本符合施工规范的要求,综合经济角度,更推荐方案一作为该深基坑现场支护结构的设计方案,并建议基坑工程实际施工时应同时兼顾安全性与经济性。
(4) 将数值模拟计算结果与现场监测数据进行了对比,结果表明模拟计算结果与实测数据具有较好的一致性,证明有限元模型计算结果的正确性和可行性,有限元模拟能够反映基坑变形的一般规律,为基坑支护结构的设计与施工提供参考。
