机载激光测深波形去噪算法对比分析

2021-03-10李厚朴翟国君

测绘学报 2021年2期

宋越，李厚朴，翟国君

1. 海军工程大学导航工程系，湖北武汉 430033； 2. 海军海洋测绘研究所, 天津 300061

机载激光测深是近20年发展起来的一种主动式海洋测量技术[1-4]，适用于水深浅于50 m的海域，具有测量精度高、机动性强、成本低等优点，能够覆盖船只无法到达的极浅区域。机载激光测深系统是利用对水体具有较强穿透能力的蓝绿色激光(532 nm)进行水域扫描，获取全波形水面、水体和水底的反射数据，从而提取水底地形、水体浑浊度等信息。

机载激光测深精度主要受到测深系统位置精度和扫描回波的提取精度影响。为提高位置精度，文献[5]结合卫星定位和惯导系统,推导出激光脚点在成图坐标系中的定位模型；文献[6]建立了参数加权最小二乘平差模型，对测深系统位置精度进行检校；文献[7]利用遥感数据对测量海域测深系统参数进行评测，提高平台作业质量从而提高定位精度。在提取高精度扫描回波方面，需要从机载激光全波形数据中精确提取水面和水底反射信号，但由于受到水体散射、噪声等因素影响，无法精确提取水面和水底反射时间间隔[8-11]。目前，国内外学者相继开展对机载激光全波形数据的去噪拟合研究，在机载激光全波形数据去噪方面，文献[12]认为应该利用高通滤波将信号中的高频信号剔除，从而达到去噪目的；文献[13]利用启发式规则来识别海面与海底反射；文献[14]利用分层异构模型进行拟合去噪；文献[15]采用去卷积法和平均差方函数法对波形预处理,通过包含距离、导数和极值约束的逐级检测确定信号的初始位置。以上方法均对回波噪声起到一定抑制效果。然而，不同去噪方法各有其优势，高通滤波选取的过滤尺度直接影响去噪效果[16]；在小波软阈值去噪中阈值、分解层级等参数选取不当，同样影响去噪效果[17]。因此，去噪算法有待进一步优化。波形处理是检验去噪效果的重要手段，并且能够提取出较为理想的波形特征信息。波形处理方法较成熟的有：峰值探测法、波形分解法和去卷积算法[18-20]。峰值探测法可直接提取峰值信息，效率较高，但易受到噪声和粗差的影响，精度较低。波形分解法是对水面、水体、水底反射回波用不同函数分别进行拟合[20-21]，拟合精度得到一定提升，但计算量较大。去卷积算法是根据信号产生的物理过程，还原原始信号，会出现信息丢失、过度分割等问题[22]。

本文利用小波软阈值去噪和EMD去噪法，研究两种方法最优参数选择，以及找到联合去噪效果的最优方案，旨在进一步提高去噪精度。由于仿真数据能够放大原始回波信号传播过程中的特点，对去噪算法效果更为敏感，方便对去噪算法进行对比研究，因此先利用仿真数据进行信号的去噪算法比较研究，再用实测数据进行去噪拟合，验证算法对数据的实际效果。

1 波形特征及信号模型构建

1.1 机载激光测深波形特征

机载激光回波信号由水面反射回波、水体散射回波、水底反射回波以及噪声4部分组成[23-24]，因此机载激光回波信号可表示为4部分信号的叠加。用式(1)表示为

y=f(t)=f(t)S+f(t)C+f(t)b+f(t)N

(1)

式中，f(t)S表示水面反射回波；f(t)C表示水体散射回波；f(t)b表示水底反射回波；f(t)N表示噪声；y为t时刻回波的振幅。由于数据处理中提取的为第2段原始波形，即海表回波和海底回波的完整回波波形，不包含发射器的出光波形，介质不均匀主要来自水体的影响，实际会造成回波波形波宽变宽、面积增大等，f(t)N主要包括背景噪声和传感器内部噪声，机载激光测深作业限于50 m以上浅海域，测量精度要求较高，因此，需要对原始波形数据在保留有效回波信号的基础上进行最大限度的去噪处理。

1.2 信号模型构建

一般认为水面反射回波服从高斯函数，水底反射如果在平坦浅海区域也可近似看作服从高斯函数，而水体反射回波服从B样条函数。文献[25]研究了高斯函数与B样条函数之间的相似关系，建立了如下逼近公式

(2)

因此，可以将无误差仿真数据进行如下表示

(3)

式中，μs、μC、μb分别为水面反射、水体散射、水底反射回波波形的对称轴；σS、σb分别为水面反射、水底反射回波波形的半幅波宽。水体反射回波信号用三次B样条近似函数的变形函数来代替，最后将初始仿真信号加入高斯随机噪声得到试验仿真数据。本文采用采样间隔为1 ns，采样点数为300进行去噪仿真分析，加入噪声后得到的仿真信号如图1所示。

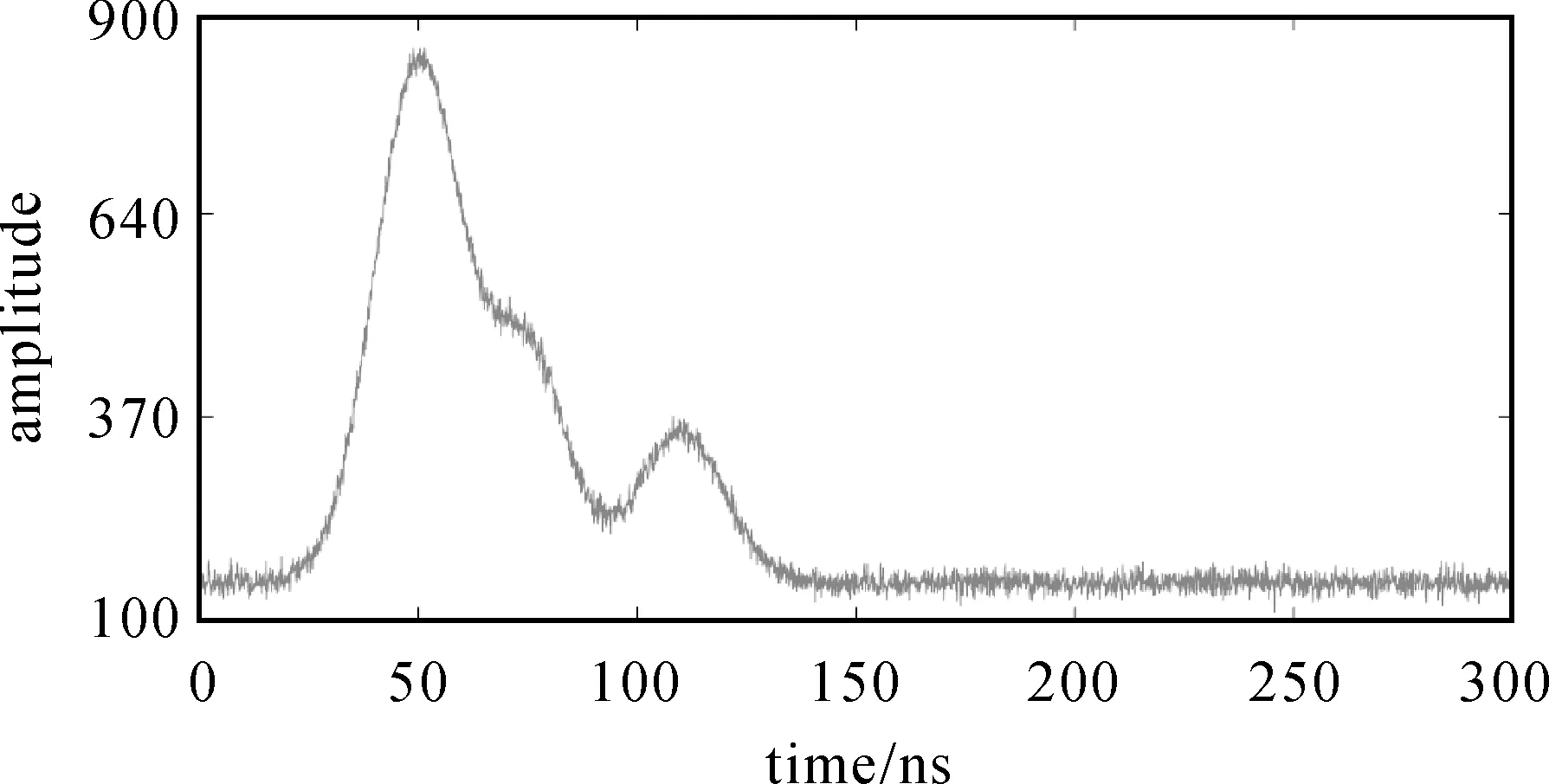
图1 加入噪声的仿真数据Fig.1 The simulation data with noise

2 波形去噪拟合算法

波形去噪是机载激光测深数据处理的关键步骤，本文对小波软阈值去噪法、EMD去噪法，与联合去噪法进行对比试验，反复调节各试验参数以达到最佳去噪效果。再利用实测数据进行去噪拟合，从而对去噪算法的实际效果做出评判。流程如图2所示。

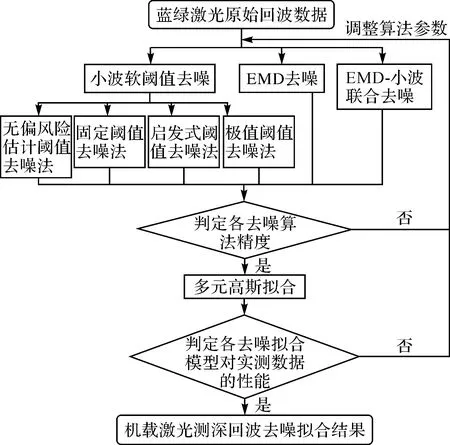
图2 本文算法流程Fig.2 Flow diagram of new algorithm

2.1 小波阈值去噪

由于小波变换为线性变换，因此经过正交变换后的回波信号可最大限度去除原始信号间的相关性。噪声经过正交变换后仍然为噪声，分布在各尺度上，不破坏各分量信号的有效信息，为去除噪声和最大保留有效信息提供基础。

小波变换后分为高频系数和低频系数。高频系数反映信号的噪声、突变等情况，低频系数反映信号的整体变化趋势和相关性等，故将小波变换后的高频信号进行小波阈值处理，阈值处理函数可分为硬阈值处理法和软阈值处理法。

软阈值处理法公式为

(4)

式中，w为小波分解系数；λ为设定的阈值；singn(w)表示取w值的正负号。

软阈值处理是对小波系数进行“收缩”处理，从而使输入和输出的曲线具有良好的连续性。大量试验以及国内外研究也发现，软阈值函数去噪优于硬阈值函数去噪[14]，故本文选用小波软阈值去噪法。小波去噪阈值主要分为以下4种。

2.1.1 无偏风险估计阈值(rigrsure)

将原始信号取绝对值从小到大排列，再各自取平方，取第k个元素的平方根作为阈值，则该阈值产生的风险为

(N-k)f(N-k)]/N

(5)

式中，N为总数据量；k表示第k个元素。因此将风险最小的元素作为无偏风险估计阈值。

2.1.2 固定阈值(sqtwolog)

(6)

2.1.3 启发式阈值(heursure)

(7)

(8)

当etacrit时选择无偏风险阈值。

2.1.4 极值阈值(minimaxi)

(9)

本文将对4种阈值方法进行逐一试验，旨在找到对机载激光回波信号去噪最优阈值算法。

2.2 经验模型(EMD)去噪

实现经验模型分解，待分解信号需满足：①信号可分为多个本征模函数；②本征模函数(IMF)既可以是线性函数也可以是非线性函数；③任意时刻，原信号可看做若干本征模函数的叠加。IMF需要满足：①IMF信号中，极值点个数与零点个数的差值至多为1；②任意阶IMF的上下包络均值为零。

从原始信号中提取全部极大值和极小值，利用三次样条函数对极大值拟合出上包络线eup(t)，对极小值拟合出下包络线edown(t),则上下包络线的均值作为原始信号的均值包络线m1(t)

(10)

再用原始信号减去均值包络线得到第1层分解系数c1(t)。重复以上步骤直至残差信号rN(t)为单调函数或常量时停止分解。故EMD分解后的最终表达式为

(11)

式中，x(t)为原始信号；ci(t)为分解得到的IMF；rN(t)为分解残差。

2.3 小波阈值分解与EMD模型联合去噪

小波阈值分解和EMD模型在信号去噪方面都有广泛应用，本文将利用两种方法进行联合去噪。针对去噪算法的特点拟定3种方案：①先进行EMD去噪，将EMD去噪后最优重构数据进行小波阈值去噪；②先进行EMD分解，对分解得到的IMF值进行小波阈值去噪，最后将去噪后IMF值进行重构；③先进行小波阈值去噪，去噪后数据进行EMD分解与重构。

2.4 基于最小二乘的波形数据多元高斯拟合

对原始回波进行去噪后会降低噪声对回波的影响外，同时也降低了回波分辨率。波形拟合能够提高浅水混叠信号以及海底较弱回波分辨率，且波形拟合是检验去噪效果好坏的一种手段。传统方法较为烦琐且由式(3)可知，三次B样条函数、双指数函数其基本形态依然是高斯函数，三次B样条函数、双指数函数可以看作是多个高斯函数的组合形式。故本文将对去噪后的实测数据进行基于最小二乘的多元高斯拟合，其基本模型为

(12)

式中，n为待定的高斯函数个数。

3 试验与分析

3.1 小波阈值去噪试验

采用4种软阈值小波去噪方式对前文得到的仿真数据进行去噪。

为使去噪后对比效果更加明显，图3为4种去噪方法经过5层小波分解去噪后与原始无噪声信号作差的去噪偏差图。图中，无偏风险估计阈值去噪法表现略差；启发式阈值去噪法与固定阈值去噪法效果相当，且均优于极值阈值去噪效果。

图3 不同阈值去噪偏差图Fig.3 Denoising deviation diagram of various threshold

由于小波分解层级是影响去噪效果的主要参数之一，因此，本文通过逐一增加分解层数来找到最佳去噪分解层，其去噪精度好坏利用均方根差(RMSE)进行判断

(13)

式中，N为信号采样数；f(ti)为去噪信号；yi为原始无噪声信号。

图4统计了4种小波阈值去噪算法一至十五阶分解层级的RMSE值，从中可以看出4种小波软阈值去噪法在前六阶分解中精度迅速提高，启发式阈值去噪六阶以后精度趋于平稳，且精度最高；其他去噪算法精度都有不同程度的下降。综上可知，小波软阈值去噪法中，启发式阈值对回波信号去噪最为理想，将分解层数设为六阶去噪效果最优。

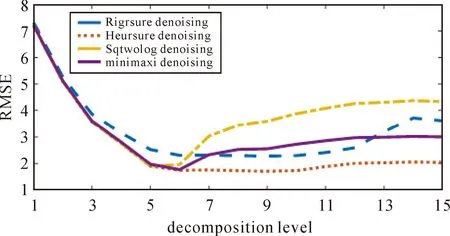
图4 小波阈值去噪分解层级精度比较Fig.4 Comparison of accuracy of wavelet threshold denoising decomposition level

3.2 经验模型去噪试验

首先将本文得到的仿真数据进行EMD分解，得到八阶IMF值如图5所示。

从图5可以看出，噪声主要集中在前四阶IMF值中，其中一阶IMF分量可以认为是纯噪声直接剔除，二至四阶分量认为是噪声与有效回波的混合层级。下面将逐一剔除每一层分量进行数据重构，观察数据变化。

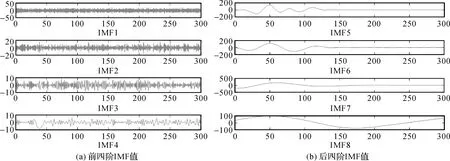
图5 经验模型八阶IMF分解量Fig.5 Eighth-order IMF decomposition of EMD

从图6可以看出：将一阶和二阶IMF剔除后信号中仍然存在较大噪声，逐一剔除一至四阶IMF分量后，原始回波信号噪声得到了一定抑制，而剔除前五阶IMF后重构回波信号开始出现信号失真，图6中的图(d)出现了较大偏差。故将一阶IMF作为纯噪声剔除，二至四阶IMF分量可看作噪声与信号的过渡层根据数据采集量的大小作适当筛选，五阶之后的IMF分量作为有效信号回波予以保留。

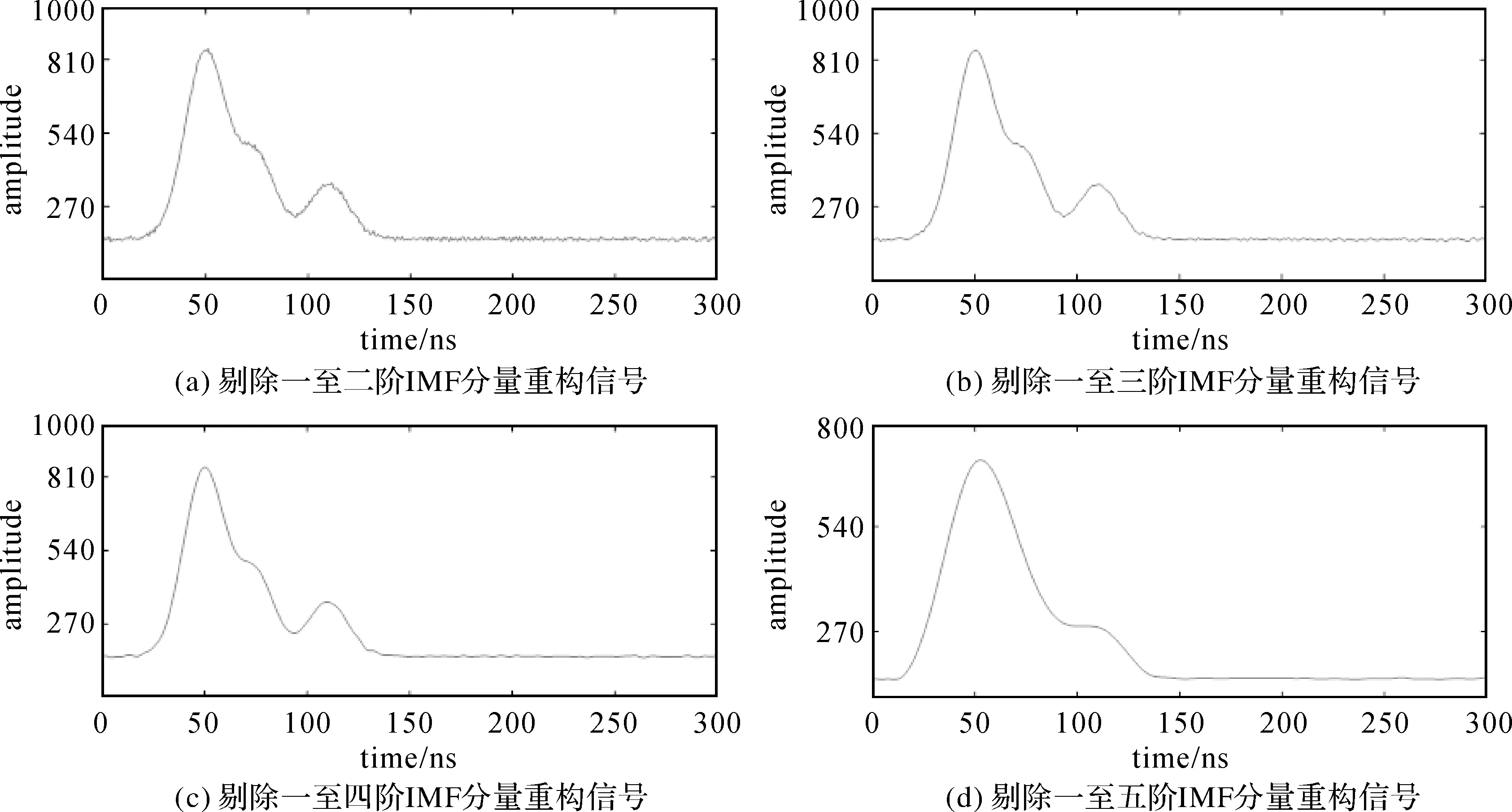
图6 逐一剔除IMF分量后的重构信号Fig.6 Reconstructed signals after removing IMF components one by one

表1给出了几种去噪方法的精度比较。从表1可以看出：启发式小波阈值去噪对激光回波去噪最为有效，精度达到1.740 6，EMD模型在剔除前四阶IMF系数后精度可达到2.030 9。为探究最佳波形去噪效果，下面将联合小波阈值去噪法和EMD去噪进行联合去噪。

表1 多种去噪方法精度对比

3.3 联合去噪试验

根据表1结果可知，方案1：将用EMD经验模型五至八阶IMF重构后的数据进行小波阈值去噪(表2)。

表2 方案1：去噪效果对比

从表2可以看出，经过EMD去噪后再进行小波阈值去噪，效果不明显精度保持不变，可见将IMF前四阶高频信号去除后，已将大量噪声剔除，同时也损失了一部分有效信息，再由小波阈值去噪时，无法探测出剩余噪声且失去的有效信息无法补偿，因此并未对精度有所提高。

方案2：先进行EMD分解，对分解得到的IMF值进行小波阈值去噪，最后将去噪后IMF进行重构。由于回波信号EMD分解有八阶IMF值，每阶IMF都用启发式阈值去噪法进行处理(从前文可知启发式阈值去噪法最优)，而处理后与处理前的IMF值重构组合数较多。本文进行了大量试验，表3列出了组合后较为明显的去噪方案。

表3 方案2：去噪效果对比

从表3可以看出，仅对第5层IMF值小波阈值去噪重构的信号与5至8层均小波去噪重构的精度一致，是因为IMF值从六阶以后为低频信号，小波阈值去噪对其去噪并不明显，而对五阶以下IMF值有一定去噪效果，且从表3的第5列和第6列精度比较可以看出，阶数越低小波阈值去噪效果越明显。

方案3:先进行小波阈值去噪，再进行EMD去噪(表4)。

由于小波去噪后信息量的减少，方案3仅得到了五阶IMF值。从表4看出，五阶IMF值均无法剔除，否则将造成有效信号的大量流失。

表4 方案3：去噪结果

综合3种方案可以看出，因为小波阈值去噪对数据的缩放尺度大于MD去噪的尺度，小波阈值去噪效果略优于EMD去噪，在经过小波阈值去噪后，EMD去噪已无法再对数据进行进一步去噪；EMD去噪后丢失的有效信息在小波去噪中无法找回，因此方案1效果不佳；可以考虑在EMD分解得到IMF值后，对高频IMF值进行小波分解，小波阈值去噪处理的高频层级越多，重构后精度提高越明显。该方法能够自由对信号中的噪声进行“拆解”与去噪，并灵活对各分量进行重构，通过逐层分解去噪，能够在信息量巨大时提取更多有效信息，且精度与小波阈值去噪相当，为测深回波信号处理提供新思路。

3.4 实测数据去噪拟合试验

为了检验去噪算法的性能和对实测数据的效果，利用2018年3月南海某海域机载激光原始波形数据进行去噪拟合试验。试验采用Mapper5000测深系统，使用4通道高速波形采集卡完成海面回波和3通道海洋波形采集，每通道采样频率达到1 GSa/a，数字分辨率为10 bit。数据采集期间，海域水质较好，飞行行高约为300 m，激光脉冲扫描天顶角设置为±15°。

3.4.1 波形去噪拟合阶数对比试验

经过仿真数据试验对比分析后，本节将利用4种小波阈值去噪算法(无偏风险估计阈值去噪法、固定阈值去噪法、启发式阈值去噪法、极值阈值去噪法)以及联合去噪中效果较好的方案2算法进行实测数据的去噪，再对去噪数据进行多元高斯拟合，讨论其最佳高斯拟合阶数。其中，从实测数据中选取了10组具有典型特征的波形进行去噪试验。

表5给出了5种去噪方法高斯拟合后的最优阶数。从表5可以看出无偏风险估计阈值去噪法拟合精度最差，固定阈值去噪法、启发式阈值去噪法和极值阈值去噪法的精度相当，在3.800至4.000之间波动，联合去噪法拟合后最优精度可以达到3.397，但需要七阶高斯拟合，相对计算量加大。

表5 不同去噪算法的高斯拟合均方根误差Tab.5 Root mean square error of Gaussian fitting of different denoising algorithms

3.4.2 波形去噪拟合性能

本节将水面反射峰值和水底反射峰值间隔不同的数据分为峰值间隔平均在75、165和215 ns的3组，每组5000条原始波形数据。对3组数据进行去噪试验，再利用3.4.1节中拟合精度较高的五阶高斯拟合算法对去噪数据进行拟合。拟合性能见表6—表8。

表6 不同去噪算法拟合性能指标对比(激光峰值间隔平均75 ns)

表7 不同去噪算法拟合性能指标对比(激光峰值间隔平均165 ns)

表8 不同去噪算法拟合性能指标对比(激光峰值间隔平均215 ns)

为检验各去噪算法的实际效果，引入以下两个指标，进行性能判定。

(1) 拟合优度R2

(14)

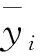
(2) 相关性系数标准差STD

STD是相关系数CORR的标准差，反映算法的稳定性。STD越接近零其算法稳健性越好

(15)

(16)

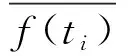
从表6—表8中可以看出：不同峰值间隔下的精度有所起伏，但固定阈值去噪法在各组数据中的去噪效果均优于其他阈值去噪法，去噪效果稳定；联合去噪法在165 ns间隔下的去噪拟合精度明显优于其他去噪法，而在峰值间隔为75 ns和215 ns的去噪拟合试验中联合去噪法拟合精度低于其他去噪算法，可见其稳定性略低于其他去噪算法；5种算法经过五阶高斯拟合后STD都极低，可见5种算法具有较强的稳健性。