基于改进鲸鱼优化算法的农业装备永磁同步电机参数辨识研究
2021-03-10崔海林
崔海林
(江苏省常州技师学院,江苏 常州 213000)
永磁同步电机(PMSM)在农业装备领域应用场合广泛,但是PMSM是一个非线性系统兼有多变量和强耦合的特征,同时受工作环境影响存在内部参数变化情况,各类观测器的估计精度和参数变化情况直接相关,严重时影响系统的稳定性。目前,精确地辨识出电机内部参数已成为当下研究热点[1]。
PMSM参数辨识方法主要分为离线式和在线式两种。离线式大体分为限元分析、实验测量两种;在线辨识可分为最小二乘法、模型参考自适应法、卡尔曼滤波法以及智能算法,其中智能算法在电机参数辨识中受到了广泛关注。文献[2]注入谐波电流来补偿模型,并运用最小二乘法和牛顿迭代法来进行参数辨识,然而该方法运算复杂;文献[3]采用并行混沌优化算法对永磁同步电机进行多参数辨识,然而对于变量多的电机优化存在计算时间长、很难搜索到最优解的问题;文献[4]提出小生境粒子群算法,运用小生境技术来克服粒子群算法存在的精度低、易发散等问题,然而该方法运算较复杂;文献[5]为了观测电机位置角度和转速,设计了滑模电流观测器,又考虑到电机易受内部环境影响而致使电机参数变化,提出了一种基于遗传算法的电机参数辨识方法,然而该方法容易出现早收敛、算法效率低等问题。文献[6]提出一种改进灰狼优化算法的参数辨识方法来进行电机参数变身比,然而该方法运行时间长,且容易陷入局部最值问题。
为了提高PMSM参数辨识性能,提出了一种改进鲸鱼优化(improved whale optimization algorithm,IWOA)算法。将随机初始化种群方式改为采用Tent映射初始化产生种群,其次在位置更新环节引入反向学习,最后建立4阶的PMSM参数辨识模型,并利用IWOA算法来辨识出PMSM参数。
1 标准WOA算法
世界上最大的哺乳动物家族是鲸鱼家族,鲸鱼可以通过回声定位来搜索附近猎物与信息交流,鲸鱼家族中的座头鲸群体有着一种特殊的觅食行为(气泡网觅食),来获取聚集的鱼虾群作为食物。模拟座头鲸觅食行为是WOA算法的起源,寻优目标设置为食物位置,算法依靠以下三环节来获取最优解:包围猎物、气泡网攻击、随机搜索。
第一步为鲸鱼包围猎物,算法优化过程中,鲸鱼的每一个位置都代表所求优化问题的一个可行解。在算法执行任务时,算法中生成个体会在初始位置随机对附近进行搜索,由于优化问题中的全局最优解在搜索过程中的位置是未知的,所以,算法通过不断的迭代过程提供当前最优解即为最接近全局最优解的位置,其他的鲸鱼根据这一当前最优解更新自身位置:

式中,D是鲸鱼个体位置和最优鲸鱼个体间的距离,t是当前算法迭代的次数,X*和X分别是最优鲸鱼个体位置和其他个体位置。A和C鲸鱼是算法的参数向量:

式中,r1,r2是[0,1]区间的随机数,a=2(1-t/tmax)即随着 t增加从2线性递减到0。
第二步是泡泡网攻击,鲸鱼在持续收缩猎物包围圈的同时做向上螺旋的捕食动作,从而捕食更多的鱼虾。根据这种捕食行为,WOA算法也有相应的两种模拟行为方法,其一是收缩包围圈,在数学模型中,通过降低式(2)中参数a的数值以实现包围圈收缩环绕机制。参数向量A是[-a,a]的随机值,当满足A是[-1,1]的随机值时即t+1时刻的鲸鱼位置一定朝着最优位置更新自身位置。其二是螺旋更新位置,鲸鱼以螺旋运动向鱼虾逼近:

上述两种行为,鲸鱼个体会同时执行,为了模拟这一情况,假设执行每一种行为概率均为0.5,得到同步模型为:

第三步为搜索猎物,在WOA算法中通过改变参数向量A实现算法的全局搜索,使得A实现满足不在[0,1]区间即可,区别于第二步中以最优鲸鱼个体位置的局部搜索,而是根据任意一个鲸鱼个体位置进行随机搜索,属于全局搜索,这一行为扩大了搜索范围即全局寻优。

式中,Xr代表任意一鲸鱼个体位置。
2 改进鲸鱼优化算法
2.1 Tent映射初始化
标准WOA算法的初始种群是依赖随机产生的,易出现初始种群分布不均情况,直接影响种群的多样性;与此同时,算法性能表现的优劣受初始种群的多样性好坏影响。数学上的混沌是将整个混沌系统视为随机来源,通过迭代函数检测这一混沌行为,不同的初始值会产生不同的序列,但是在无穷大的迭代次数下每一个序列都会有一个相同的极限值,这一特征即是混沌行为的遍历性。一组输入值就存在有一组输出值与之对应,这一特征即是映射,与此同时,如果在一个确定性系统中出现不可预测情况即是混沌现象。为了让WOA算法产生较好多样性的初始种群,依据前面所述的混沌行为优点,引入混沌映射。在优化领域中,常采用Logistic映射,其数学方程见式(6),但是这一映射存在遍历均匀性不足的缺陷(呈两头多、中间少)。相较于Logistic映射,Tent映射可以产生更加均匀的分布即在[0,1]区间内初值分布更均匀。Logistic映射数学方程为:

式中,xn=[0,1],n=1,2,...∞。
Tent映射数学方程为:

式中,当u=1/2时产生的分布序列最为均匀,参数的变化对分布密度影响最小,此时式(7)变形为典型Tent映射形式:

为了获得具有多样性的初始种群,提高算法的求解效率,具有分布均匀的初始种群由Tent映射方法来产生,初始种群X为:

式中,Xmax为X的取值上界,Xmin为X的取值下界,xn为序列迭代至n步时的值。
2.2 反向学习策略
针对标准WOA算法后期易陷入局部最优的情况,引入反向学习策略优化。反向学习(OBL)策略其主要思想是寻找出当前可行解及求取反向解并进行排序择优,从可提高算法的搜索能力。在d维空间中存在一点Z(x1,x2,...xn)且 xi∈[ai,bi],则其反向点为其中
在鲸鱼个体更新时刻的位置环节增加反向学习,即通过随机产生一个[0,1]范围内的随机数与设置反向学习概率p比较,小于或等于时执行反向学习操作,其方程为:

经反向学习变异后可得到新的鲸鱼种群同时应重新计算适应度值并择优。
3 PMSM参数辨识模型
在简化条件下[5],PMSM模型在dq轴坐标系下数学方程描述为:

式中,id、iq和 ud、uq分别为 dq 轴电流、电压;Ld、Lq为 dq轴电感;Rs、ψf和ω分别为定子电阻、永磁转子磁链、转子机械角速度;ψd、ψq为dq轴定子磁链。
PMSM可采用id=0控制并离散化得到:

式(13)是一个秩为2的方程组,但存在4个待辨识参数,得到基于式(13)的2阶的欠秩模型不易准确辨识出参数值。在d轴中注入id≠0值的电流,获得另一个2阶模型,进一步地将2个2阶模型合并,从而得到4阶PMSMdq轴辨识模型。
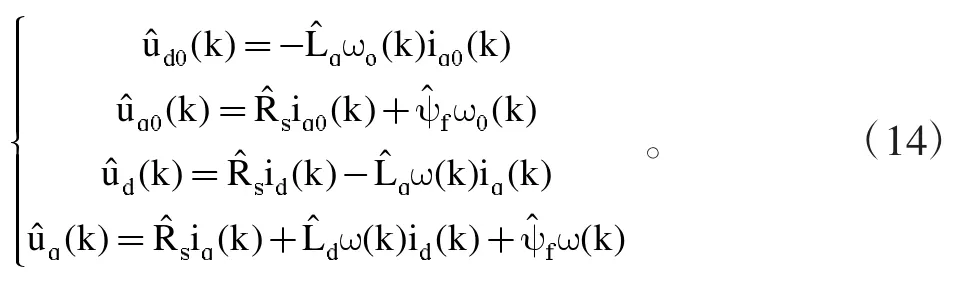
4 基于IWOA算法的PMSM参数辨识
将辨识PMSM参数问题转化为系统优化问题,重点在于设计适应度函数,通过理论模型和实际系统同一输入,同时IWOA筛选待辨识参数最优值,使得理论模型和实际系统之间的目标函数值趋于零即辨识参数值与实际值一致。PMSM参数辨识模型如图1所示,适应度函数数学形式如下:
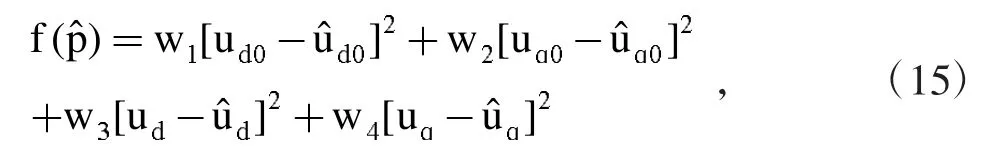
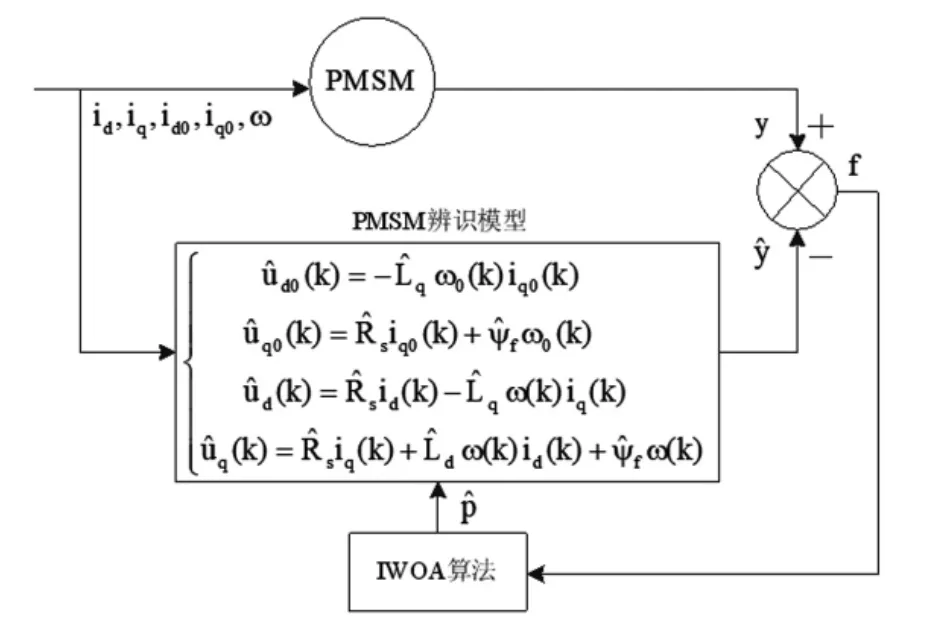
图1 PMSM参数辨识模型
式中,w1,w2,w3和 w4为权重,均取值 0.25,即 4 个变量同等重要。
5 实验仿真
5.1 IWOA算法性能验证
为验证IWOA算法性能,选择2个基准函数作为测试,分别为Sphere函数和Girewank函数,其函数具体信息详见文献[7],Sphere函数是单峰函数,Girewank是多峰函数。为了对照和公平,引入标准WOA算法作为对照组,同时实验参数设置一致(最大迭代次数为150、种群规模为30),对于每一测试函数,两种算法均独立运行10次,收敛曲线见图2。从图2中可以看到,相较于标准WOA算法,IWOA算法表现更好,特别是面对多峰函数,WOA算法获得最终值时存在偶然性,有陷入局部最优情况,而IWOA算法表现良好。通过算法性能验证环节,验证了IWOA算法的收敛精度高、收敛速度快。
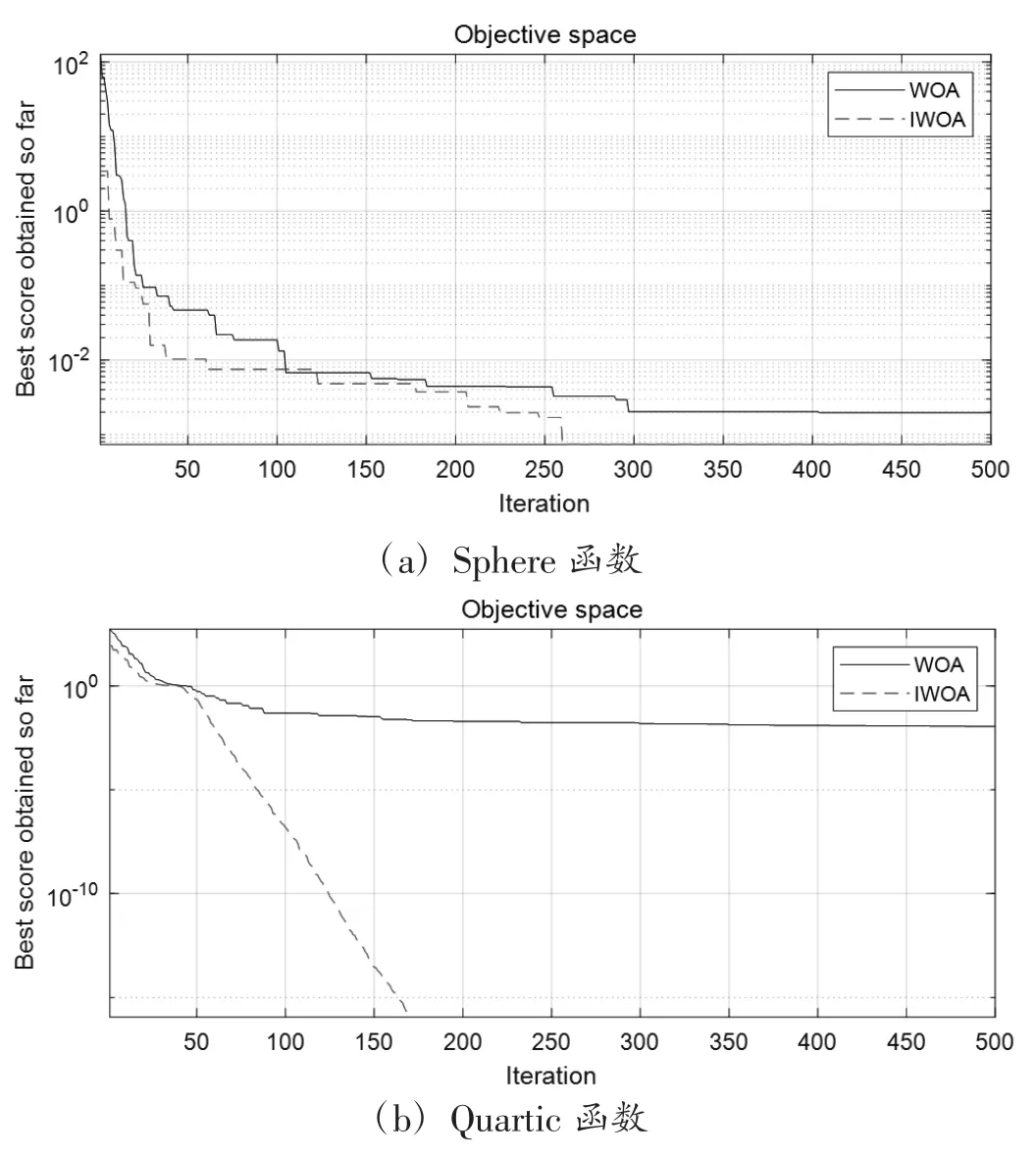
图2 2个标准测试函数的收敛曲线
5.2 参数辨识实验
为了验证PMSM参数辨识的可行性和采用IWOA算法辨识参数的有效性,在Matlab中构建PMSM参数辨识模型,模型整体框图见图3。本节的算法参数设置同5.1节,PMSM参数值情况详见文献[6],待辨识参数的初始范围为[0,10],远离实验电机设计值,排除干扰。
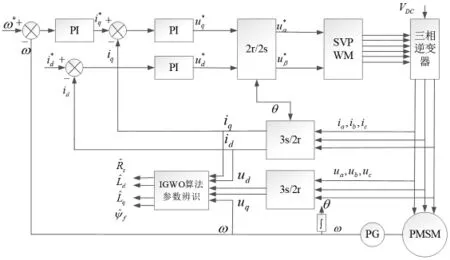
图3 PMSM参数辨识仿真框图

表1 两种算法的优化结果
表1给出了WOA算法和IWOA算法对电机参数的辨识结果,可以看到,相较于WOA算法,IWOA算法的辨识精度更高,更加接近真实数值,特别是d轴电感的辨识精度。适应度值结果也表明,IWOA算法的收敛速度和收敛精度好。
6 结论
为精确地辨识PMSM参数,本文设计了一种IWOA算法并建立参数辨识系统。在WOA算法的基础上基于Tent映射进行种群初始化,其次在位置更新环节引入反向学习。仿真结果表明,IGWO算法能够快速准确地辨识出PMSM参数。
