工业机器人摩擦补偿方法研究

殷兴国

摘要：关节摩擦力是影响工业机器人的运动平稳、碰撞检测的灵敏性及拖拽示教的平滑性的关键因素，如何确定摩擦力的大小是工业机器人的控制难点。针对工业机器人摩擦力的计算和补偿问题，本文在传统鲁棒自适应方法的基础上引入权重因子，实现一种基于角色切换的摩擦补偿，进而提出了两种有效的自适应摩擦补偿方法，并证明了其在控制器应用中的稳定性，最后在连杆系统中用仿真的方法验证了两种补偿方法的有效性，并比较了它们的优缺点。

关键词：工业机器人摩擦补偿自适应连杆系统

Abstract： Joint friction is the key factor affecting the motion stability of industrial robot， the sensitivity of collision detection and the smoothness of drag teaching. How to determine the friction is the difficulty point of industrial robot control. Aiming at the problem of friction calculation and compensation of industrial robot， based on the traditional robust adaptive method， this paper introduces the weight factor to realize a friction compensation based on role switching， then proposes two effective adaptive friction compensation methods， and proves their stability in the application of controller， Finally， the effectiveness of the two compensation methods is verified by simulation in the connecting rod system， and their advantages and disadvantages are compared.

Key Words： Industrial robot; Friction compensation; Adaptive; Connecting rod system

随着近些年机器人摩擦补偿方法研究的不断深入，机器人摩擦补偿方法也多种多样。实际上，机器人摩擦补偿方案的选取受到许多因素的影响，包括可用的执行器信息、传感器信息等。因此，以不同的可用摩擦信息作为依据，本文详细阐述机器人摩擦补偿的研究进展。

假设摩擦模型是已知的并且参数可以被得到，此时，人们可以通过摩擦参数辨识的方法实现机器人摩擦的补偿。基于给定的摩擦模型，人们可以采用离线的机器人摩擦参数辨识方法，并根据辨识好的参数在工程中实现机器人的摩擦补偿[1，2]。摩擦力模型主要經历了库伦摩擦模型、静摩擦+库伦摩擦模型、Stribeck模型和LuGre模型等[3]，吴晓敏等在Stribeck模型基础上加入了温度项[4]，Johanastrom等在LuGre模型基础上分析粘滑运动[5]，此外，针对模型参数皆已知的动态摩擦模型[6]，Kosti等运用观测器的方法观测动态摩擦模型的内核态，实现固定模型、参数的动态摩擦补偿[7]。不仅如此，还将鲁棒方法导入机器人模型的获取中，从而在已知模型的基础上，令人满意地补偿机器人中的摩擦力[8]。

针对摩擦模型已知，但参数未知的情况，自适应方法是补偿摩擦的一种常见方案[9]。对于摩擦模型未知的情况，人们常常将鲁棒方法应用于机器人的摩擦补偿。此外，一些先进的智能工具也被使用到机器人摩擦补偿的方案中。模糊、神经网络[10-12]、强化学习[13]等智能工具通过构建机器人摩擦模型或者自调节控制参数等方法[14]，对机器人的摩擦进行补偿。

然而，对于上述的绝大部分摩擦补偿方法而言，摩擦被视为一种有害于机器人系统稳定的扰动，对其进行补偿。但实际情况下，摩擦并不一定有害于系统的稳定。出于利用摩擦稳定系统的考虑，本文在传统鲁棒自适应方法的基础上引入权重因子，实现一种基于角色切换的摩擦补偿。

针对模型已知参数未知的静摩擦，引入了权重因子，并将其运用在基于模型的两种机器人鲁棒自适应摩擦补偿方法中.通过权重因子，一方面，当摩擦有害于机器人系统稳定时对摩擦进行补偿抵消;另一方面，当摩擦有益于系统稳定时，对摩擦进行利用。最后，通过仿真验证了引入权重因子后，鲁棒自适应摩擦补偿方法能够减小跟踪误差以及控制力矩。

2系统建模

考虑机器人动力学模型，有一些常见的可用于控制律设计的性质，主要归纳为以下几点。

第一，惯量矩阵的正定性。

在大多数摩擦补偿的方法中，摩擦常常被当作一种有害的因素进行抵消或者补偿。但是在很多实际工况中，摩擦常常有利于系统的运动，例如，机械臂可以利用摩擦进行制动。在机器人轨迹跟踪中，摩擦所扮演的角色也不仅仅是有害者，有时候摩擦也能利于机器人的轨迹跟踪。而如何判定摩擦在机器人跟踪轨迹中是有益还是有害，并以此为依据设计控制律，从而实现，一方面，在摩擦有益之时利用摩擦，另一方面，在摩擦有害之时补偿摩擦，是本部分重点关注的问题。而摩擦利用的判据与机器人系统李雅普诺夫的稳定性紧密相关。在这里，考虑对摩擦有利或者有害的判据设定为，摩擦是否能够保证给定拟李雅普诺夫函数的导数始终不大于0，并以此为依据，设计连续的权重因子，并提出鲁棒自适应框架下的基于角色切换的机器人摩擦补偿方法。

考虑基于关节空间的机器人动力学模型可以描述为如下欧拉-拉格朗日方程的形式，并将摩擦力显式表达出来，如下：

其中，是机器人在关节空间中的坐标，为机器人惯量矩阵，表示机器人柯氏力与离心力，表示机器人重力，表示机器人摩擦力，表示各关节输入力矩，为机器人雅各比矩阵。

第四，摩擦中的权重因子设计。

在大多数情况下，摩擦阻碍物体的相对运动或者相对运动趋势。据此对机器人中的摩擦力方向提出如下合理假定：

下面对权重因子的设计思想进行详细阐述。

当摩擦力使系统靠近滑模面时，摩擦力有利于系统的稳定，权重因子设定为0。

当摩擦力使系统状态远离滑模面时，摩擦力不利于系统的稳定，权重因子设定为1。也就是说，权重因子可以根据摩擦力在轨迹跟踪中所扮演的角色，即有益者或者有害者，适时并连续地取值，从而达到，一方面，在摩擦有益于稳定之时利用摩擦，另一方面，在摩擦有害于稳定之时补偿摩擦的效果，因而可以实现控制律利用摩擦和补偿摩擦的角色切换。

在實际工程中，受到不同机械结构、环境、任务等因素的影响，人们所能得到的机器人摩擦信息不尽相同。很多情况下，机器人摩擦的模型很难准确得到。据此，根据摩擦模型能否准确得到，本文分别设计基于摩擦模型的鲁棒自适应摩擦补偿和不基于摩擦模型的鲁棒自适应摩擦补偿。两者均是J.J.Slotine提出的机器人自适应补偿框架下进行摩擦补偿的。

考虑库伦-粘性的静态摩擦模型：

与机器人动力学参数可线性化类似，摩擦参数线性化的形式可以推导为：

虽然说摩擦模型可以得到，但是摩擦参数可能存在一定的误差，即精确的的值很难得到。不仅如此，机器人动力学参数也存在不确定性，即人们很难得到精确的的值。因而，鉴于机器人动力学和摩擦均存在一定的参数不确定性，本文提出下述定理。

2.1使用速度信息的自适应摩擦补偿方法

考虑机器人动力学模型和摩擦模型。假定机器人摩擦满足假设，那么提出控制律：

即各关节轨迹误差趋于下述滑模面：

所以跟踪位置、速度误差渐近收敛到0，定理证明完毕。

结合权重因子和自适应控制律，对角色切换进行详尽分析。

（1）当时，结合假设，中关于摩擦的项可能不小于0，此时无法保证机器人跟踪轨迹的稳定性，需要对摩擦项进行处理。因而选取。当时，该控制律与传统的基于模型的鲁棒自适应摩擦补偿方法相同，此时摩擦有害于机器人轨迹跟踪的稳定，因而采用自适应的方法抵消摩擦。

（2）当时，结合假设，中关于摩擦的项不大于0，此时即使对摩擦不做处理，机器人轨迹跟踪的稳定性也能得到保证。当时，控制律中与摩擦相关的项将不作用于系统的控制力矩。控制律无需对摩擦进行处理，此时的摩擦将有利于机器人轨迹跟踪的稳定。当时，对摩擦的处理介于上述两者之间，目的是保证控制律的连续性。

注意到定理一的证明不涉及矩阵A和矩阵B。这意味着，该摩擦力补偿方法不仅能应用于库伦-粘性静态摩擦模型。只要摩擦模型满足参数线性化性质和假设，权重因子就可以引入到基于摩擦模型的鲁棒自适应补偿方法中，从而实现基于角色切换的摩擦补偿。例如，在Stribeck模型线性参数未知而非线性参数已知的情况下，该基于角色切换的摩擦补偿方法同样适用。

为了减少摩擦角色切换中产生的抖振现象，本方法在权重因子中引入了边界层，以保证切换过程的连续性。对于大多数引入边界层来减少抖振的控制律，系统严格意义上的渐近稳定性难以保证，闭环系统最终收敛到平衡点的有界邻域内。而在本方法中，边界层的引入只改变了利用摩擦与不利用摩擦的作用区间，虽然会影响角色切换的效果，但是并不影响摩擦补偿的稳定性，机器人系统严格意义上的稳定性仍能得到保证。

该方法针对的是机器人摩擦参数未知的情形。如果摩擦参数精确已知时，亦可以将权重因子运用在摩擦的精确抵消上。通过权重因子的引入，我们只需要精确抵消不利于机器人轨迹跟踪稳定时的摩擦即可。

在实际的机器人摩擦补偿中，权重因子的引入将带来更多的可调节参数。本方法可以通过设计权重因子中和的值，来合理地选取不利用摩擦与摩擦利用的作用区间，从而实现更好的摩擦补偿的性能。

注意到上述摩擦补偿的方法用到了速度信息。但是在实际机器人系统中，相比位置信息而言，获取的速度信息会有较大的误差。不仅如此，速度信息会比位置信息存在更大的噪声干扰。因而文献提出了一种通过代替来实现的自适应摩擦补偿。而同样地，权重因子也可以引入到该自适应摩擦补偿方法中，作为定理一的补充和扩展。

2.2使用参考速度信息的自适应摩擦补偿方法

考虑机器人动力学模型和库伦+粘性摩擦模型。假定机器人摩擦模型满足矩阵A与矩阵B的对角元均不小于0，那么提出如下控制律：

所以跟踪位置、速度误差渐近收敛到0，定理证明完毕。

定理一与定理二的控制律不同点在于，摩擦补偿项里面的自变量由变为了，即定理二中关于摩擦补偿的项为，而定理一中针对摩擦补偿的项为。虽然如此，该自适应摩擦补偿方法仍涉及了速度信息，但这种方法引入权重因子后亦能够实现基于角色切换的摩擦补偿效果。

3连杆系统仿真验证

考虑二连杆大负载机械臂抓取模型，如图1所示。

其他固定的机械臂动力学参数如表1所示。

假定二连杆机械臂受到较大的摩擦。其真实的摩擦模型设定为：

其次，本仿真给出待估计摩擦模型和机械臂动力学模型的初始估计参数。这里待估计的机械臂动力学初始参数与摩擦参数初始值为：

最后设定跟踪轨迹及控制律参数。机械臂跟踪的目标曲线设定为：

鲁棒自适应参数的值设置如下：

4基于摩擦模型的鲁棒自适应摩擦补偿仿真

本部分主要描述基于模型的摩擦自适应补偿的二连杆大负载机械臂仿真。权重因子中的参数选取为：

与之对应的，不利用摩擦的权重因子选取为1，即对于任意的。那么

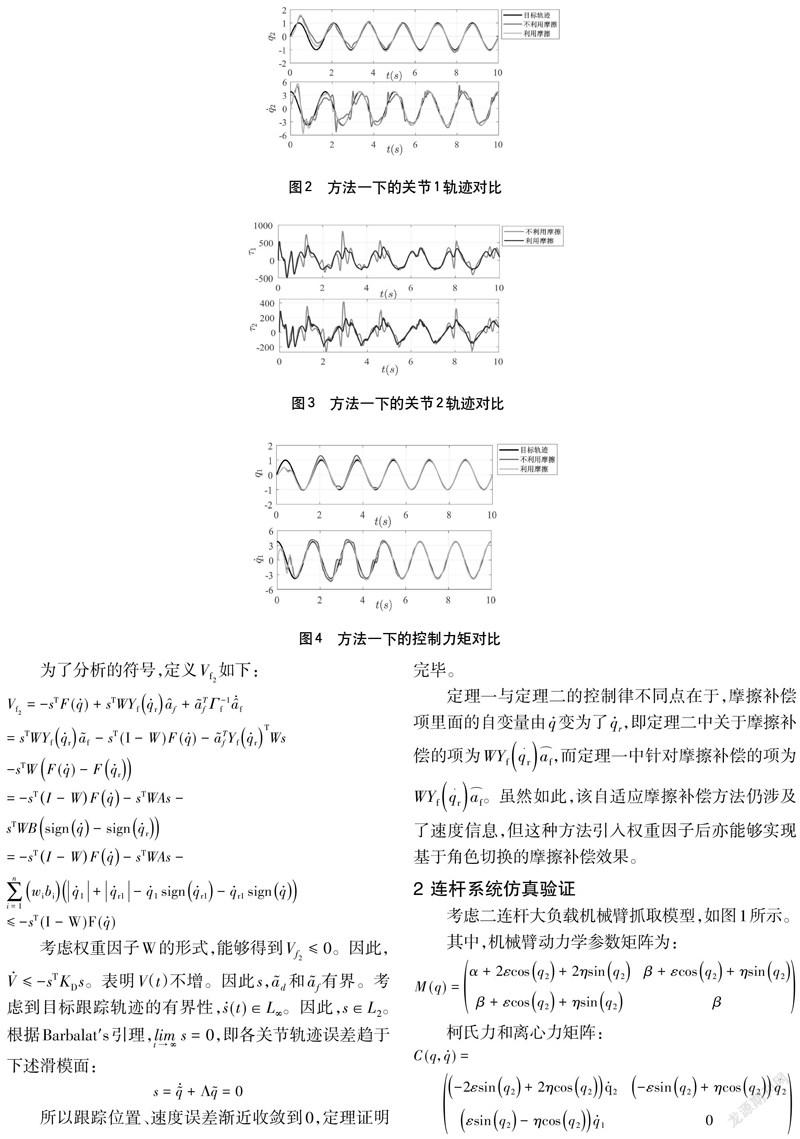
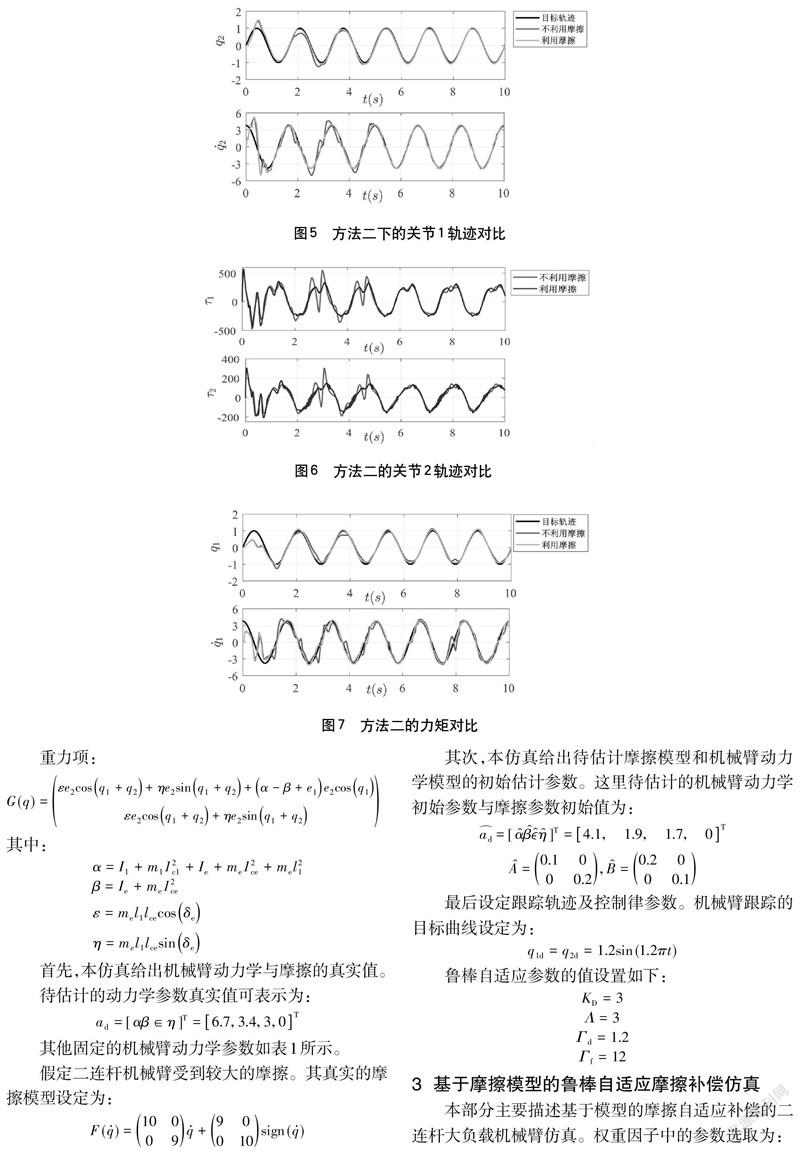
，下列图2～7中表示了在方法一、方法二控制律下机械臂的位置、速度和力矩。显然，权重因子的引入不影响机械臂跟踪的稳定性，机械臂的位置误差和速度误差均收敛到0。

为了能够从数值上更好地描述引入权重因子所带来的优化效果，仿真取前10s，引入如下表征量：

其中：

可以表征位置和速度的跟踪误差，可以表征系统力矩的大小。也就是说，越大，一定程度上意味着机械臂跟踪位置速度误差越大;越大，意味着机械臂跟踪所消耗的能量越大。那么，有无权重因子的仿真效果对比如表2所示。

上表可以清楚地表明，利用摩擦的自适应补偿方法所对应的表征量将小于不利用摩擦所对应的表征量。也就是说，从仿真效果上看，基于摩擦模型的角色切换鲁棒自适应摩擦补偿方法可以实现减小跟踪误差和控制力矩的效果。因而，摩擦模型已知的基于角色切換的鲁棒自适应摩擦补偿，能够一定程度上提升跟踪精度，减小控制的能量消耗，因而在工业上有着较强的应用价值。

5结语

本文提出了两种用于工业机器人控制器中的摩擦补偿方法，用理论和实验仿真的方法验证了所提出方法的有效性，并通过仿真对比得出鲁棒自适应摩擦补偿在工业应用上更有优势。

参考文献

[1]J.SweversW.Verdonck，J.DeSchutter.DynamicModelIdentificationforIndustrialRobots[J].IEEEControlSystemsMagazine，2007，27：58-71.

[2]储婷婷.基于多轴耦合同步控制的机器人高精度轨迹跟踪方法研究[D].哈尔滨：哈尔滨工业大学，2015.

[3]李雨健.六轴码垛机器人的轨迹规划与关节摩擦补偿研究[D].哈尔滨：哈尔滨工业大学，2017.

[4]吴晓敏，刘暾东，贺苗，高凤强，邵桂芳.机器人关节摩擦建模与补偿研究[J].仪器仪表学报，2018，39（10）：44-50.

[5]K.Johanastrom，C.Canudas-de-Wit.RevisitingtheLuGrefrictionmodel[J].IEEEControlSystemsMagazine，2008，28：101-114.

[6]D.Kostic，BramdeJager，M.Steinbuch，etal.Modelingandidentificationforhigh-performancerobotcontrol：anRRR-roboticarmcasestudy[J].IEEETransactionsonControlSystemsTechnology，2004，12：904-919.

[7]B.Armstrong，O.Khatib，J.Burdick.TheexplicitdynamicmodelandinertialparametersofthePUMA560arm[J].IEEEInternationalConferenceonRoboticsandAutomation，1986，3：510-518..

[8]HaoLei，PaganiRoberto，BeschiManuel，etal.DynamicandFrictionParametersofanIndustrialRobot：Identification，ComparisonandRepetitivenessAnalysis[J].Robotics，2021，10（1）：49.

[9]MadsenEmil，RosenlundOlufSkov，BrandtDavid，etal.AdaptivefeedforwardcontrolofacollaborativeindustrialrobotmanipulatorusinganovelextensionoftheGeneralizedMaxwell-Slipfrictionmodel[J].MechanismandMachineTheory，2021，155：104-109.

[10]W.He，A.O.David，Z.Yin，etal.NeuralNetworkControlofaRoboticManipulatorWithInputDeadzoneandOutputConstraint[J].IEEETransactionsonSystems，Man，andCybernetics：Systems，2016，46：759-770.

[11]李敏，王家序，肖科，等.基于模糊RBF神经网络动态摩擦分块补偿的机器人数字鲁棒滑模控制算法[J].中国机械工程，2012，23（23）：2792-2796.

[12]贺苗，吴晓敏，邵桂芳，等.基于RBFNN的机器人关节摩擦建模与补偿研究[J].仪器仪表学报，2020，41（11）：278-284.

[13]张竞.工业机器人关节摩擦补偿策略研究[D].厦门：厦门大学，2019.

[14]ShuzhiS.Ge，C.C.Hang，L.C.Woon.Adaptiveneuralnetworkcontrolofrobotmanipulatorsintaskspace[J].IEEETransactionsonIndustrialElectronics，1997，44：746-752.

3299500338258