Sn、SnS、Cu、Cu2S分解、挥发及相互反应的热力学分析与讨论

张 博,刘大春,熊 恒,周正恩,邓 勇,杨 斌,李 玲,徐宝强

(1.复杂有色金属资源清洁利用国家重点实验室,云南昆明 650093;2.昆明理工大学真空冶金国家工程实验室,云南昆明 650093;3.云南省有色金属真空冶金重点实验室,云南昆明 650093;4.北京科技大学冶金与生态工程学院,北京 100083;5.北京安泰科信息股份有限公司,北京 100083)

标准吉布斯自由能ΔrGθ和吉布斯自由能ΔrG是确定反应过程进行方向的主要热力学量[1]。通过标准吉布斯自由能ΔrGθ和吉布斯自由能ΔrG的计算结果,不仅可以预测材料制备和冶金过程中反应的基本规律,还可作为相关工艺的理论基础。饱和蒸气压是纯物质的特性,可用来作为纯物质挥发性判断的依据[2]。本文采用经典热力学计算了不同条件下Sn、SnS、Cu、Cu2S分解、挥发及相互反应ΔG-T关系,以及锡的饱和蒸气压等数。

1 理论基础

1.1 吉布斯自由能

吉布斯自由能在冶金过程中有重要的地位。在冶金和材料热力学分析中,标准吉布斯自由能的计算是主要的指标。它是判断和控制相关反应在一定条件下发生的趋势、方向以及达到平衡的重要参数[3-6]。一般用范特霍夫化学反应等温方程式,计算推导实际条件下反应的吉布斯自由能变化ΔrG,可以判断反应过程进行的方向,计算公式见式(1)～(3)。

式中:Kθ为标准平衡常数;ΔrGθ为标准状态下的吉布斯自由能变化;Q为实际条件下反应前后物质的压力或浓度(活度)之比;ΔrG为实际条件下的吉布斯自由能变化。

当ΔrG为负值且其数值越大时,反应向指定方向进行的可能性就越大。ΔrGθ负值越大,表明生成的化合物越稳定,也表示在标准状态下反应自发进行的可能性越高。由ΔrGθ可以求出标准平衡常数Kθ,从而知道反应进行的程度[3,7]。

对于一个化学反应,判断该反应是否达到平衡,是通过反应物之间的相关关系确认[2-3]。若参与反应的物质中有任意两个物质不能共存时,则该反应未能达到平衡。判断化学反应是否达到热力学平衡,可采用以下方法:①相图分析;②热力学参数状态图分析;③热力学计算ΔrGθ进行判断。

1.2 纯物质饱和蒸气压

纯物质在一定的温度和压强下有固定的蒸气压和分子结构,用克劳修斯-克莱普方程表示,见式(4)。

在某一温度下,金属的饱和蒸汽压越大,其越容易挥发,纯物质的温度与饱和蒸气压的关系式如式(5)所示。

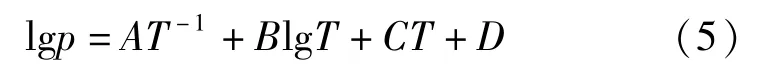
式中A、B、C、D均为常数[8]。

2 结果与讨论

采用经典热力学方法,计算出各体系的ΔG-T关系,计算结果如表1～9所示。通过查阅数据,获得Sn 的A、B、C、D 值,得到Sn 的饱和蒸气压P-T关系式。

2.1 SnS分解与挥发的热力学分析与讨论

由表1 绘制SnS(s,l)分解热力学平衡图,结果如图1所示,在图中可以直观看到参与反应各物质的稳定区域及稳定条件。

表1 SnS(s,l)分解反应ΔG-T 关系

直线上方区域内,任一温度下,实际硫压高于平衡线上相同温度时的平衡硫分压,故平衡线上方区域为SnS 的稳定区,下方为Sn 的稳定区。图中绘出两个相变点,1 154 K 时SnS 的熔点和505 K 时Sn 的熔点,以及SnS(s)、SnS(l)、Sn(s)、Sn(l)的稳定区。由图1 可判断各物质稳定存在的条件,如:505 K时,若SnS(s)发生分解,则有lg(Ps2/Pθ＜1.02 ×10-26,即硫分压小于1.02 × 10-27MPa(1.021 ×10-21Pa);1 154 K 时,若SnS(l)发生分解,需要压力小于1.02 ×10-7MPa(0.102 1 Pa)。

图1 Sn-S 系平衡图

由图1 可见,SnS(s,l)分解的温度与压强呈负相关性。随着压强的增大,SnS(s,l)发生分解所需要的温度也越低,当SnS(s,l)在1 154 K 发生分解,此时需要的压强为0.102 1 Pa,远远小于标准大气压,故认为SnS(s,l)在标准状态下的分解反应不会发生。

由表2 绘制气态SnS分解反应热力学平衡图,结果如图2所示。

表2 SnS(g)分解反应ΔG-T 关系

根据图2 及等温方程可以判断各物质存在的稳定区域,标准状态下,SnS 的沸点是1 503 K。由图2可以看出:当温度T＞1 503 K 时,SnS 为气态,此时气态的SnS 若发生分解反应,其平衡常数小于1(平衡常数大于1,反应才会发生),故气态SnS 的分解反应不可能发生。

图2 气态SnS分解反应平衡图

由表3 绘制得SnS(s,l)挥发热力学平衡图,结果如图3所示。

表3 SnS(s,l)挥发反应ΔG-T 关系

图3 SnS 挥发热力学平衡图

平衡线下方区域为SnS(g)的稳定区,上方为SnS(l)、SnS(s)的稳定区。图中绘出一个相变点,1 154 K时SnS 的熔点。由图3 可判断各物质稳定存在的条件,如:当T=1 260 K 时,若SnS 挥发,需要lg(Ps2/Pθ)＜1.02 ×10-1,即压力小于1.02 ×10-2MPa(1.02 ×104Pa);当T=840 K 时,若SnS 挥发,需要lg(Ps2/Pθ)＜1.02 ×10-5,即压力小于1.02 ×10-6MPa(1.02 Pa)。

由图3 可见,SnS(s,l)挥发的温度与压强呈负相关性。随着压强的增大,SnS(s,l)挥发所需要的温度也越低,当压强为1.02 Pa,SnS(s,l)在840 K 时会挥发,当压强为1.02×104Pa,SnS(s,l)在1 260 K 时会挥发,故认为SnS(s,l)在真空条件下的挥发容易。

2.2 Cu2S分解与挥发的热力学分析与讨论

由表4 绘制Cu2S(s,l)分解反应热力学平衡图,结果如图4所示。

表4 Cu2S(s,l)分解反应ΔG-T 关系

图4 Cu-S 系平衡图

平衡线上方区域为Cu2S 的稳定区,下方为Cu的稳定区。图中绘出两个相变点,1 357 K 时Cu 的熔点和1 403 K 时Cu2S 的熔点,及Cu2S(s)、Cu2S(l)、Cu(s)、Cu(l)的稳定区。由图4 可判断各物质稳定存在的条件,如:1 403 K 时,若Cu2S(l)发生分解,lg(Ps2/Pθ)＜1.02 × 10-6,即S 分压小于1.02 ×10-7MPa(0.102 Pa);1 357 K 时,Cu2S(s)发生分解需要压力小于1.02 ×10-8MPa(1.02 ×10-2Pa)。

由图4 可见,Cu2S(s,l)分解的温度与压强呈负相关性。随着压强的增大,Cu2S(s,l)发生分解所需要的温度也越低,当Cu2S(s,l)在1 357 K 发生分解,此时需要的压强为0.010 2 Pa,远远小于标准大气压,故认为Cu2S(s,l)在标准状态下的分解反应不会发生。

由表5 绘制Cu2S 挥发热力学平衡图,结果如图5所示。

图5 Cu2S 挥发热力学平衡图

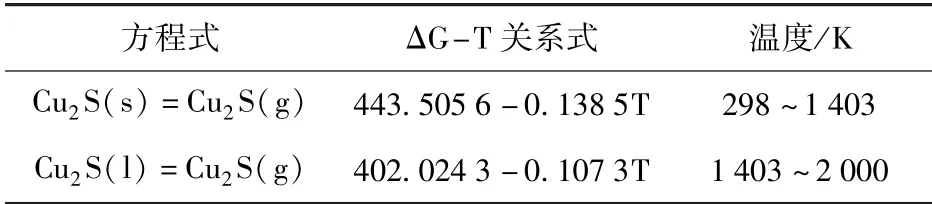
表5 Cu2S(s,l)挥发反应ΔG-T 关系

平衡线下方区域为Cu2S(g)的稳定区,上方为Cu2S(s)、Cu2S(l)的稳定区。图中绘出一个相变点,1 403 K 时Cu2S 的熔点。由图5 可判断各物质稳定存在的条件,如:当T=1 403 K 时,若Cu2S 挥发,需要lg(PCu2S/Pθ)＜1.02 ×10-9,即压力小于1.02 ×10-10MPa(1.02 ×10-4Pa)。

由图5 可见,Cu2S(s,l)挥发的温度与压强呈负相关性。随着压强的增大,Cu2S(s,l)挥发所需要的温度也越低,当压强为1.02 ×10-4Pa,Cu2S(s,l)在1 403 K 时会挥发,其压强远远小于标准大气压,故认为Cu2S(s,l)在标准状态下的挥发不发生。

2.3 Cu、Sn 挥发的热力学分析与讨论

2.3.1 Cu 挥发的热力学分析与讨论

由表6 绘制Cu(s,l)挥发的热力学平衡图,如图6所示。

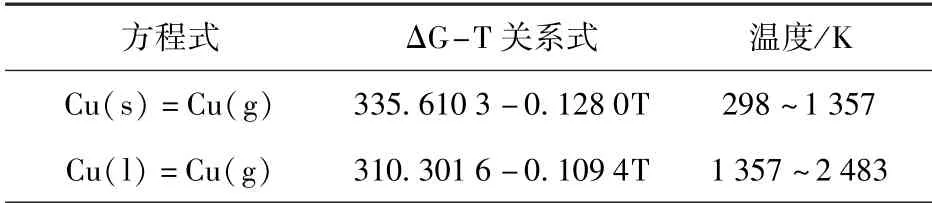
表6 Cu(s,l)挥发反应ΔG-T 关系

平衡线下方区域为Cu(g)的稳定区,上方为Cu(s)、Cu(l)的稳定区。图中绘出一个相变点,1 357 K 时Cu 的熔点。由图6 即可判断各物质稳定存在的条件。如:当T=1 357 K 时,若气态Cu 存在,需要lg(PCu/Pθ)＜1.02 × 10-6,即压力小于1.02 ×10-7MPa(0.102 Pa)。

图6 Cu 挥发的热力学平衡图

由图6 可见,Cu(s,l)挥发的温度与压强呈负相关性。随着压强的增大,Cu(s,l)挥发所需要的温度也越低,当压强为0.102 Pa 时,Cu(s,l)在1 357 K会挥发,故认为Cu(s,l)在标准状态下的挥发不会发生。

2.3.2 Sn 挥发的热力学分析与讨论

由表7 绘制Sn 的P-T图,结果如图7所示。

表7 Sn 饱和蒸汽压(P-T 关系)

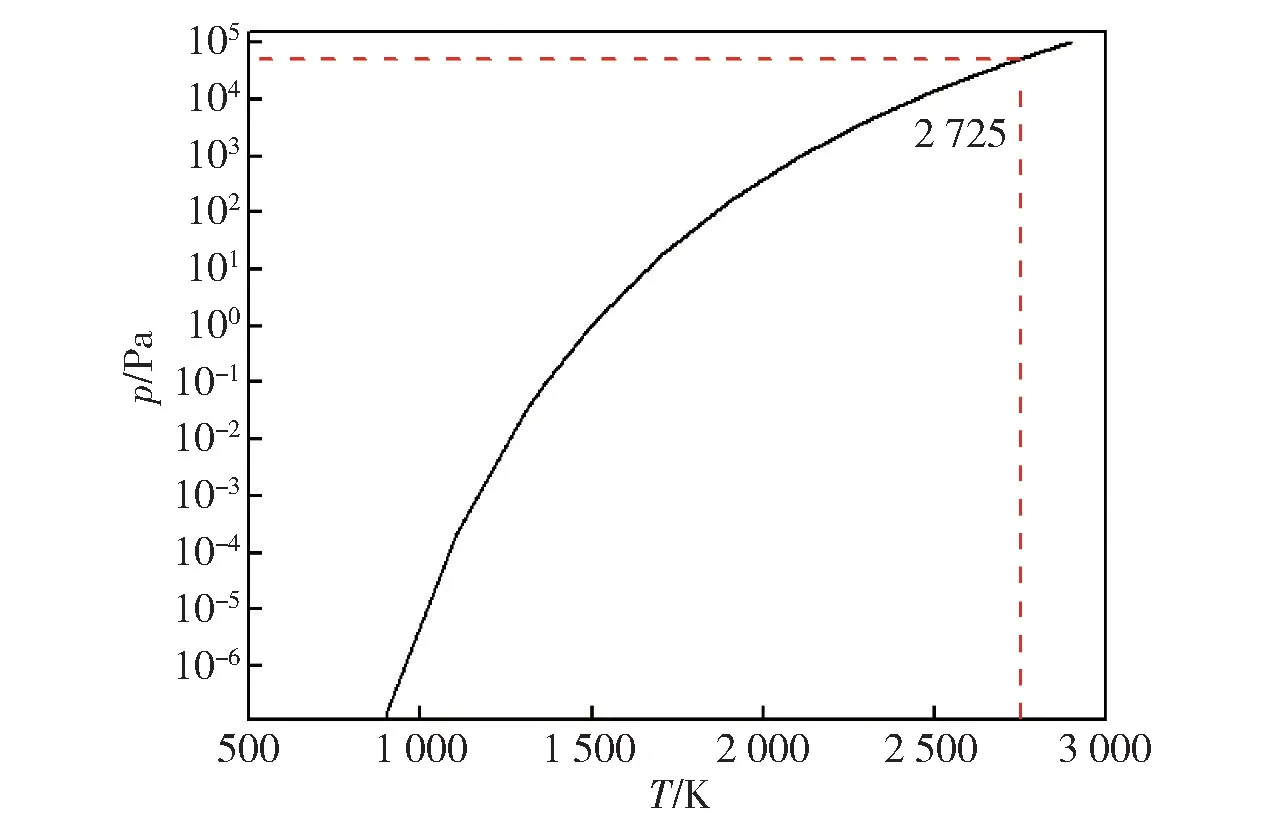
图7 Sn 的P-T 图

图7 是Sn 的饱和蒸汽压曲线。由图7 中可以得到:在T=2 725 K 时,Sn 的饱和蒸汽压小于标准大气压。Sn 的饱和蒸气压与温度成正相关性,随着温度降低,Sn 的饱和蒸汽压也随之降低。因此在Sn标准状态下很难挥发。

2.4 SnS、Cu、Sn 与Cu2 S 交互反应的热力学分析与讨论

2.4.1 SnS 与Cu 反应的热力学分析与讨论

由表8 绘制SnS 与Cu 反应的热力学ΔG-T 图,结果如图8所示。

表8 SnS 与Cu 反应的ΔG-T 关系

图8 是SnS 与Cu 标准状态下反应的热力学ΔGT图,纵坐标是ΔG值,横坐标是温度,505 K、1 154 K分别是Sn、SnS 的熔点。由图8 可以得出:标准状态下,SnS 和Cu 发生反应的吉布斯自由能随着温度的升高,ΔG值逐渐减小;在T=690 K 时,ΔG=0,T＞690 K 时,ΔG恒小于零。因此,标准状态下,SnS 与Cu 发生反应时的温度大于690 K(约417 ℃)。

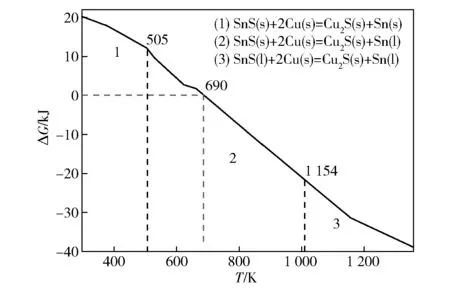
图8 SnS 与Cu 反应的ΔG 与温度T 的关系

2.4.2 Sn 与Cu2S 反应的热力学分析与讨论

由表9 计算结果绘制了Sn 与Cu2S 反应的热力学ΔG-T图,结果如图9所示。

表9 Sn 与Cu2S 反应的ΔG-T 关系

由图9 可以得出:Sn 与Cu2S 反应的热力学ΔG值随着温度T值的升高而降低,且在不同的压强、同一温度下,ΔG值的变化明显。说明真空条件下Cu2S 和Sn 的反应容易发生,而且随着压强的减小,所需的反应温度也随之降低。

图9 Sn 与Cu2S 反应的ΔG 与温度T 的关系

3 结论

本文通过对Sn、SnS、Cu、Cu2S分解、挥发反应及相互反应ΔG-T关系的热力学计算,及Sn 的饱和蒸气压的分析与讨论,得到以下结论。

1)SnS(s,l)分解的温度与压强呈负相关性。随着压强的增大,SnS(s,l)发生分解所需要的温度也越低,当SnS(s,l)在1 154 K 发生分解,此时需要的压强为0.102 1 Pa,远远小于标准大气压,故SnS(s,l)在标准状态下的分解反应不会发生;SnS(g)的分解反应不可能发生;当压强为1.02 Pa时,SnS(s,l)在840 K 会挥发,当压强为1.02 ×104Pa 时,SnS(s,l)在1 260 K 会挥发,故SnS(s,l)在真空条件下的挥发容易。即SnS 在真空条件下有较强的挥发性。

2)Cu2S(s,l)分解的温度与压强呈负相关性。随着压强的增大,Cu2S(s,l)发生分解所需要的温度也越低,当Cu2S(s,l)在1 357 K 发生分解,此时需要的压强为0.010 2 Pa,远远小于标准大气压,故认为Cu2S(s,l)在标准状态下的分解反应不会发生;Cu2S(s,l)挥发的温度与压强呈负相关性,随着压强的增大,Cu2S(s,l)挥发所需要的温度也越低,当压强为1.02 ×10-4Pa,Cu2S(s,l)在1 403 K 时会挥发,其压强远远小于标准大气压,故认为Cu2S(s,l)在标准状态下的挥发不发生。

3)标准状态下,当温度大于690 K(约417 ℃)时,SnS 与Cu 即可发生反应;真空条件下,Cu2S 和Sn 的反应很容易发生(如20 Pa,777 ℃时);随着压强的减小,硫化亚铜和Sn 发生反应所需温度随之降低。