基于修正遗传算法的夏玉米作物系数及蒸散发估算
2021-03-09王振龙刘竹梅吕海深丁佳楠陆云燕王怡宁
王振龙,刘竹梅,吕海深,丁佳楠,陆云燕,王怡宁
1.安徽省(水利部淮委)水利科学研究院/水利水资源安徽省重点实验室/五道沟水文水资源实验站,安徽 蚌埠 233000;2.河海大学理学院,江苏 南京 210098;3.南京水利科学研究院,江苏 南京 210029
淮河流域是中国重要的农业生产基地,夏玉米是淮河流域主要的秋粮作物,对当地经济发展及人民食品安全至关重要(张建军等,2014;袁宏伟等,2018)。蒸散量是土壤蒸发量和作物蒸腾量之和,对地表能量循环和水循环有着非常重要的作用(Xu et al.,2005;赵静等,2009;张淑杰等,2010;Lievens et al.,2017)。无水分胁迫时,作物系数是实际蒸散量与参考作物蒸散量的比值,是估算作物蒸散量的关键指标(汪顺生等,2013;王维等,2015)。根据方法不同,可计算双作物系数(Rosa et al.,2012;Ding et al.,2013)和单作物系数(李毅等,2018);根据时间尺度不同,可计算逐日作物系数(韩文霆等,2018)、旬作物系数(卢晓鹏等,2012)、月作物系数(云文丽等,2013)以及年平均作物系数(李波等,2020),进而可计算月平均蒸散量(涂安国等,2017)、各季节平均蒸散量(刘玉汐等,2019)或年平均蒸散量(吴文玉等,2013)。对于作物系数模型的建立,许多学者尝试用优化算法进行研究:王怡宁等(2020)利用通径分析筛选作物系数的影响因子,并结合BP神经网络建立夏玉米作物系数模型,该模型对夏玉米蒸散量的预测误差较小,准确率高于70%,但不足之处在于,没有提出基于关键影响因子的蒸散量预测的具体概念性模型;金菊良等(2017)利用遗传算法对无受旱的大豆作物系数及水分胁迫系数进行求解,建立了大豆作物系数模型,模型对大豆无受旱胁迫时的蒸散量估算误差较小,均方根误差均小于0.3 mm·d−1,但由于土壤水分胁迫系数也是由遗传算法模拟得到,不是逐日实测值,故模型在估算受旱胁迫的大豆蒸散量时误差增大;袁宏伟等(2018)利用遗传算法优化太阳辐射参数,得到无受旱的玉米作物系数模型,该模型对无受旱玉米蒸散量的整体估算效果较好,优于FAO-56推荐值的估算结果,但在估算受旱玉米蒸散量时误差明显增大,且没有提出对应的解决方法,使得模型总体上低估了玉米的蒸发蒸腾量。
遗传算法是常用的寻优算法,可在搜索空间中全局搜索最优解(李华昌等,2005),但已有的研究一般只针对使用算法对各生育期作物系数进行寻优求解,未考虑到对算法输出结果误差的修正,简单地寻优求解并不一定适合所有地区的数据,因此对算法输出结果进行修正是有必要的。本文利用遗传算法,并结合单作物系数法,建立五道沟地区夏玉米作物系数模型,并利用叶面积指数对模型进行修正,得到误差更小的夏玉米作物系数及蒸散量估算模型。
1 研究方法与数据来源
1.1 实验区概况
实验区位于安徽省蚌埠市固镇县五道沟水文实验站,地处淮北平原南部,站内共有62套大型地中蒸渗仪群、10套大型称重式蒸渗仪及自动高精度气象站,设有蒸散发、气象要素、潜水蒸发及土壤水分等观测场地,地下水位埋深及年变幅为1—3 m,作物主要是冬小麦、大豆、夏玉米。土壤类型主要为砂姜黑土和黄潮土,分别占淮北平原土壤总面积的54%和33%,凋萎含水率为10%—13%,田间持水率为28%—30%(范月等,2020)。
1.2 实验设计与资料选取
本文研究土质为砂姜黑土,夏玉米生育期内逐日蒸散数据由称重式蒸渗仪自动采集,蒸渗仪型号为FR101A,分辨率为0.025 mm,口径面积4.0 m2,土柱高为4.0 m,蒸散数据每10分钟记录一次。蒸渗仪上方设有摄像机,可每时自动获取作物生长图像,便于划分生长阶段。蒸渗仪内10、30、50、100、200 cm埋深处各设有时域反射仪(TDR),通过土壤水分传感器(型号为AV-EC5,分辨率为0.1%,精度为±3%,量程为 0—饱和,),每小时测量1次筒内土壤体积含水率。场地设有高精度气象站,可每10分钟获取1次空气湿度、风向、净辐射等不同气象数据,测量准确度为±5%,可用于计算参考作物蒸散量。
研究资料选取称重式蒸渗仪地下水埋深为1 m、2018年6月22日—2018年10月8日的资料及同期气象数据。由实测资料可知,2018年全年降雨量为1352.6 mm,最高日平均温度为32.8 ℃。夏玉米全生育期内无明显高温干旱或洪涝等自然灾害,作物仅接受自然降雨,无人工灌溉。蒸散量在8月8日、8月9日受人为活动干扰,数据异常,建模分析时应剔除并进行插补。
1.3 生长阶段划分
FAO推荐将生育期划分为 4个生长阶段:初期、发育期、中期和后期。根据实验区夏玉米实际生长图像,使用 PS软件勾选作物像素以及土壤像素,像素之比便视为夏玉米的地面覆盖率,将其各生长阶段划分见表1。

表1 夏玉米生长阶段划分Table 1 Summer maize growth stage division
1.4 参考作物蒸散量
用来计算 ET0的方法很多,最常用的是Penman-Monteith法,它将多种影响因素考虑在内,且在气候差异较大的地区计算精度高,但该方法的缺点是需要的气象资料较多,计算过程复杂,因此,联合国粮农组织(FAO)修正了该公式,提出FAO Penman-Monteith公式来计算参考作物蒸散量(康燕霞等,2009)。公式如下:
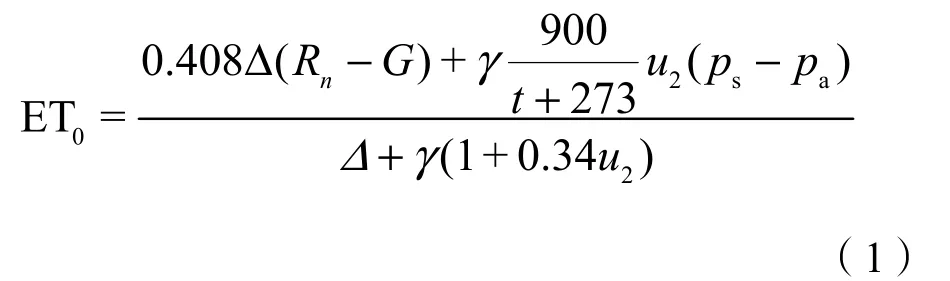
式中,ET0为参考作物蒸散量(mm·d−1);Rn为地表净辐射量[MJ·(m2·d)−1];G为土壤热通量[MJ·(m2·d)−1];t为日平均气温(℃);u2为地面 2 m高处的平均风速(m·s−1);ps为饱和水汽压(kPa);pa为实际水汽压(kPa);Δ为饱和水汽压与温度曲线的斜率(kPa·℃−1);γ为干湿表常数(kPa·℃−1),各数据取自高精度气象站(赵勇等,2005)。
1.5 土壤水分胁迫系数的计算
土壤水分胁迫系数反映出土壤水分亏缺对作物蒸散发的抑制作用,本文用下式计算:

式中,Ksi为第i天的土壤水分胁迫系数;θi为第i天0—40 cm的平均土壤质量含水率;θ10i、θ30i为第i天10 cm、30 cm处的平均体积含水率;ρb为0—40 cm 的土壤容重(1.4 g·cm−3);θw为凋萎含水率,取10%;θf为田间持水率,取28%。
2 模型建立与评价体系
2.1 模型构建
2.1.1 FAO单作物系数模型
根据有无土壤水分胁迫,分两种情况具体讨论:
在无土壤水分胁迫的条件时,作物的生长发育不会因为土壤中水分亏缺而受到抑制,其生长过程的影响因素主要为气象条件、作物本身的生长发育特征以及土壤的物理特性,计算公式如下:

式中,ETc为实际蒸散量(mm·d−1);Kc为作物系数;ET0为参考作物蒸散量(mm·d−1)。
在有土壤水分胁迫的条件时,夏玉米的生长发育过程不仅会受到上述因素的影响,还会受到土壤水分亏缺的抑制作用,故添加水分胁迫系数Ks来调整实际蒸散量,计算公式如下:

2.1.2 遗传算法模型
对于遗传算法的原理,它是将实际问题的可能解集看作种群,每个个体都经过特定的基因编码,并组成染色体。利用编码产生初始种群后,采用适者生存、优胜劣汰的原理,根据适应度大小选择存留的优秀个体,再组合交叉和变异,产生出新一代的种群,循环往复,逐代进化产生越来越好的近似解,它对结果沿多种路线平行搜索,会避免局部较优解,得到全局最优点,是一种全局最优化方法(乔均俭等,2007)。
算法流程为:设定初始参数;随机产生初始种群;个体适应度评价;轮盘赌选择存留个体;染色体交叉;染色体变异;对变异后的种群适应度值进行评估;终止条件的判断,若终止,则输出最优染色体及其适应度值,否则,返回轮盘赌再选择新的存留个体。
本文遗传算法模型的建立过程是:将夏玉米生育期分为4个阶段,分别为初期、发育期、中期和后期。选择初期、中期、后期训练集中无水分胁迫的资料,优化变量为上述阶段的作物系数,利用式(4)构造无水分胁迫时的目标函数,见式(6),再利用遗传算法寻优求解最优作物系数:

约束条件为:

式中,n为各研究阶段无土壤水分胁迫的天数;KCini、KCmin、KCend为初期、中期、后期的作物系数。
2.2 模型评价指标体系
选用精度评价指标:平均绝对误差Ema、均方根误差Erms、相关系数r及准确率P;对于作物系数,定义绝对误差在0.15、0.2、0.3以内的数据个数占总数据个数的比例为相应准确率,记为P0.15、P0.2和P0.3;对于蒸散量,定义绝对误差在2、3、4 mm·d−1以内的数据个数占总数据个数的比例为相应准确率,记为P2、P3和P4。计算公式如下所示:

式中,yi为实测值;yi′为模型模拟值;为模拟值的平均值;为实测值的平均值;i为各研究阶段的样本个数,i=1, 2, …,m,m为各研究阶段的样本总数。
评价规则为:Ema、Erms越小,r越接近1,模型的拟合准确度越高,可信度越高,预测能力越强。
3 研究结果与讨论
3.1 遗传算法模型
将夏玉米的各生长阶段按7∶3的比例划分训练集与检验集,遗传算法输出初期、中期、后期作物系数最优解见表2,表中作物系数均为阶段平均值。

表2 遗传算法作物系数最优解Table 2 Optimal solution of crop coefficient based on genetic algorithm
由表2可知,初期作物系数最小,为0.280;中期作物系数最大,为0.611。整体上,从初期到中期,作物系数呈增加趋势,从中期到后期,作物系数呈减小趋势。绘制全生育期实测蒸散量与实际作物系数见图 1,总体上,蒸散量与作物系数的变化过程是一致的。受人为活动的干扰,蒸散量在8月8日、8月9日显示数据异常,蒸散量出现了极小值,9月3日、9月4日为大风天气,董旭光等(2016)研究发现,对ET0影响较大的因子为风速,二者有显著的正相关关系,这与王希等(2013)、张杨等(2018)的研究结果是一致的。故当风速较大时,蒸散量增加,ET0也会增大,此时作物系数会出现异常波动,所以在接下来建模分析时,应合理剔除异常数据,并用邻近平均值进行插补。
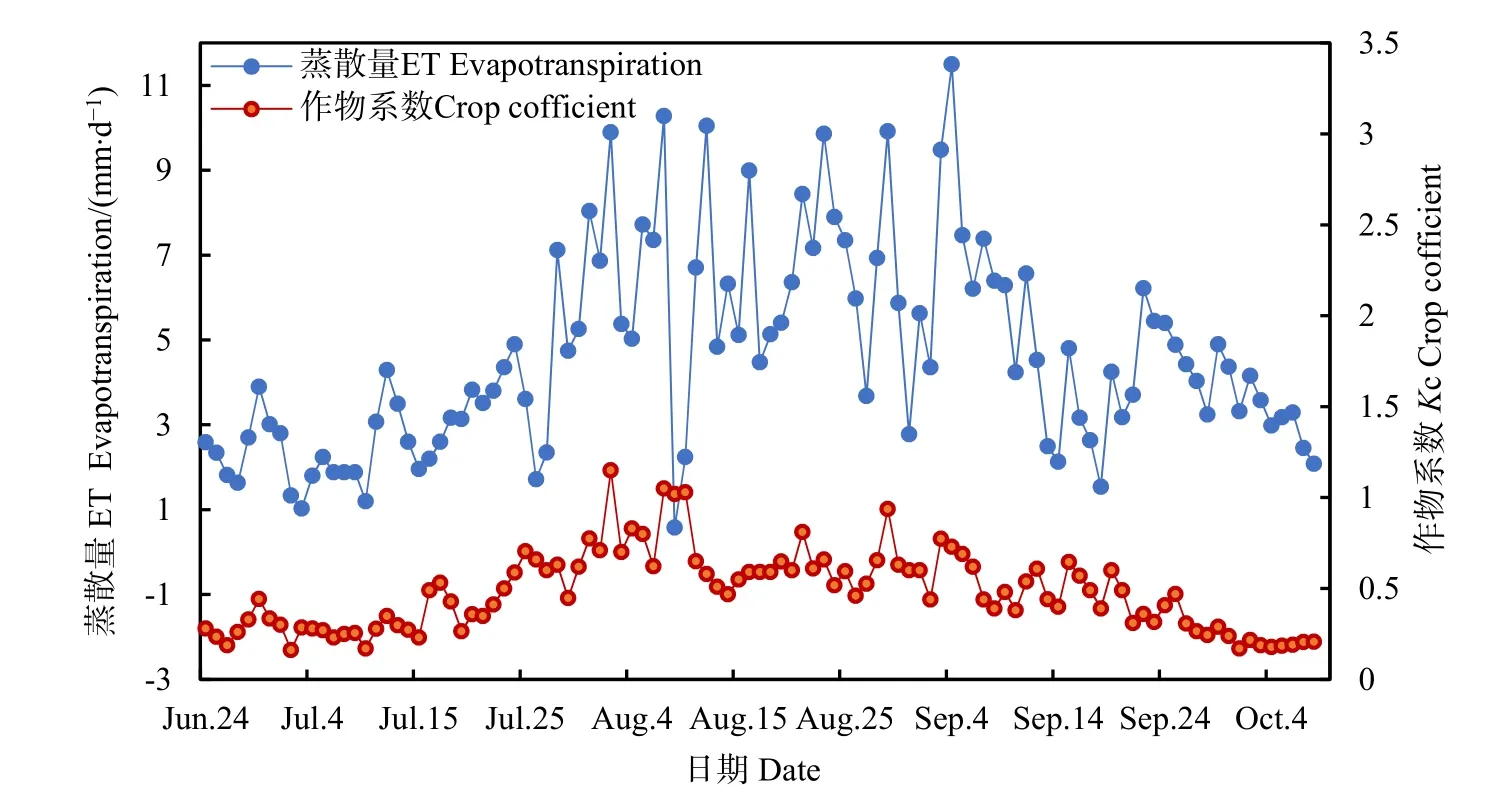
图1 全生育期蒸散量与作物系数Fig.1 Evapotranspiration and crop coefficient in whole growth period
3.1.1 作物系数的比较
由遗传算法得到不同样本模拟值与实测值的精度结果,见表 3。除发育期外,其他作物系数的计算误差MAE、RMSE均小于0.2,说明利用遗传算法得到的作物系数对实际值的拟合及预测精度较高,用该模型估算夏玉米蒸散量是可行的。
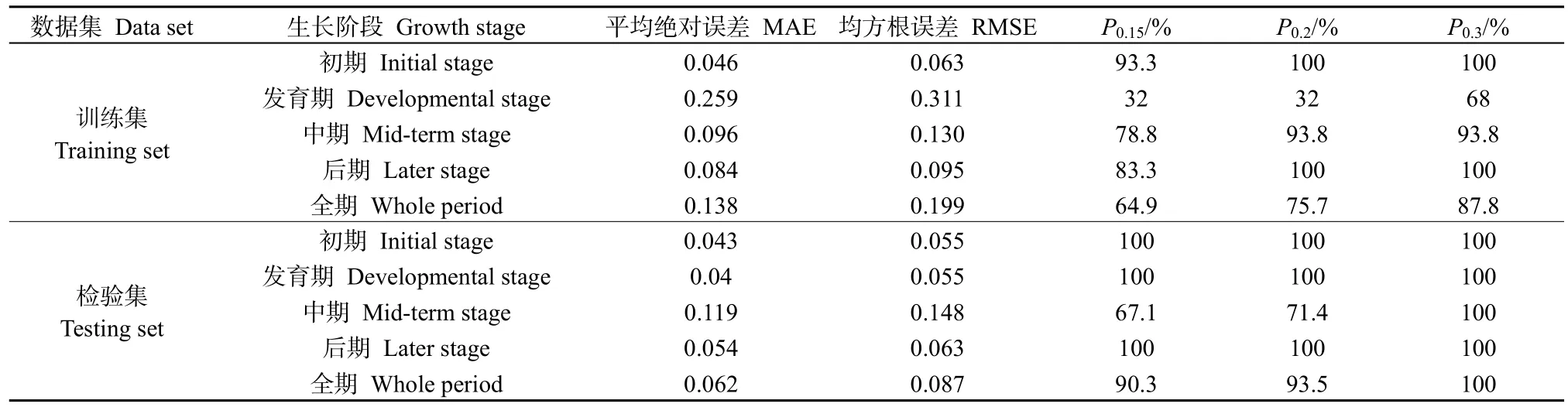
表3 不同样本作物系数拟合精度值Table 3 Fitting accuracy of crop coefficients of different samples
FAO认为将初期与中期的作物系数进行线性插补,即可得到发育期作物系数的日变化值(宋迪等,2009)。本文针对发育期阶段,若简单地将遗传算法输出值进行线性插补,得到的发育期作物系数拟合值与真实值误差较大,故需进一步对发育期作物系数线性插补值进行调整以提高精度。
3.1.2 发育期作物系数的修正
有学者研究表示作物系数与当地的植被指数存在联系(Campos et al.,2017),受此启发,绘制全生育期作物系数与叶面积指数实际值图,见图2。叶面积指数在全生育期内呈现先增后减的规律,其变化趋势与作物系数变化基本一致。在夏玉米生长前期,即本文所划分的初期与发育期阶段,叶面积指数均呈增加的趋势,尤其在发育期阶段,叶面积指数增大明显,玉米蒸腾作用变强,总蒸散量主要来自作物蒸腾,作物系数随着作物的生长而变化,且随着时间的推移,叶面积指数与作物系数呈现出较好的一致性,故引入叶面积指数和发育期天数来构建作物系数修正模型是合理的。

图2 全生育期作物系数实际值与叶面积指数实际值Fig.2 Actual crop coefficient and actual LAI in whole growth period
考虑先将作物系数线性插补值与叶面积指数相乘,根据其变化特征,再将该乘积与某个指数函数、多项式函数、幂函数或有理函数等结合,选择精度最高的函数,从而实现对发育期作物系数插补值的修正,模型式如下:

式中,Kc′为修正后的发育期作物系数;Kc″为发育期作物系数的线性插补值;LAI为发育期叶面积指数;f(x)为上述备选函数之一,x为发育期天数,x≤35 且x∈N*。
利用 MATLAB软件,根据最小二乘法原理,对模型式中的f(x)进行拟合,得到各f(x)的残差平方和SSE,拟合精度R2和均方根误差RMSE见表4。

表4 不同f (x)的拟合精度值Table 4 Fitting accuracy of different f (x)
由表4可知,尝试多种函数形式对f(x)进行拟合,R2均高于0.8,说明作物系数与叶面积指数、发育期天数之间确实存在显著的函数关系。其中有理函数的拟合精度最高,R2达到0.92,故选择有理函数加入模型式(11),最终修正模型式如下:

式中符号含义同式(11)。
利用式(12)修正作物系数模型,各精度值见表5。

表5 作物系数修正前后拟合精度值Table 5 Fitting accuracy of crop coefficient before and after adjustment
由表5可知,发育期的作物系数线性插补值经过模型修正后,其与实际值的误差有明显减小,且准确率P0.15、P0.2和P0.3有明显提高,说明修正模型可用于发育期作物系数的调整。
3.1.3 修正后蒸散量的比较
图3是训练样本中,遗传算法预测蒸散量与实际值的对比。二者平均绝对误差为0.786 mm·d−1,均方根误差为 1.12 mm·d−1,P2为 91.9%,P3为97.3%,P4为100%,借助单作物系数法,修正后的遗传算法模型得到的蒸散量与实际值拟合较好。

图3 训练集计算蒸散量与实际值比较Fig.3 Calculated ET compared with actual value in training set
图4是检验样本中,预测蒸散量与实际值的对比。二者的拟合程度较高,平均绝对误差为 1.148 mm·d−1,均方根误差为 1.61 mm·d−1,P2为 77.4%,P3为90.3%,P4为100%,说明本文模型对夏玉米蒸散量的预测效果较好。
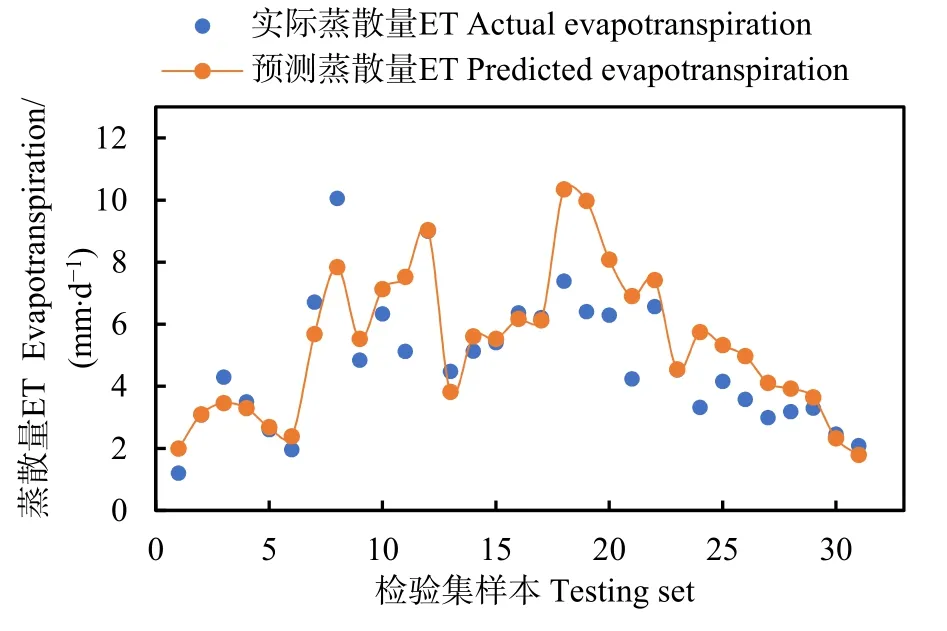
图4 检验集计算蒸散量与实际值比较Fig.4 Calculated ET compared with actual in testing set
表6是修正后遗传算法模型模拟蒸散量的精度评价表。由表3、5、6可知,修正后的遗传算法模型在拟合夏玉米作物系数、蒸散量方面精度较高,各误差均保持在较小水平内。为进一步确定模型的适用性,本文将修正遗传算法模型与FAO推荐作物系数模型的拟合精度进行比较。
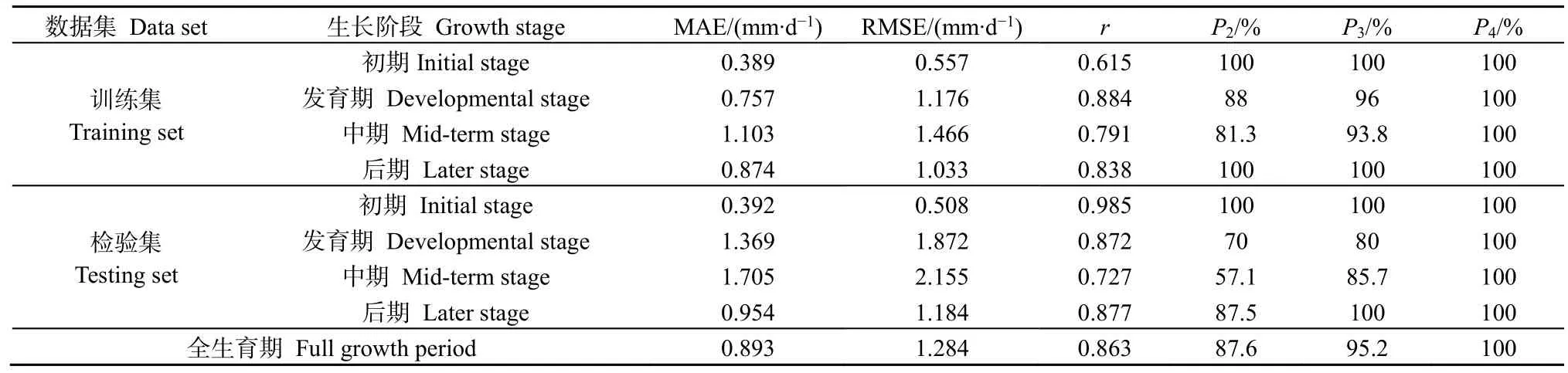
表6 不同样本蒸散量拟合精度值Table 6 Fitting accuracy of evapotranspiration of different samples
3.2 修正遗传算法模型与FAO推荐作物系数模型的比较
3.2.1 作物系数的对比
FAO推荐的夏玉米各生长阶段作物系数分别为:初期0.3,中期1.2,后期0.6(刘钰等,2000);计算全生育期逐日作物系数,两种模型的拟合精度见表 7,可以看出,使用修正遗传算法模型得到的作物系数拟合精度更高,可以满足精度要求。
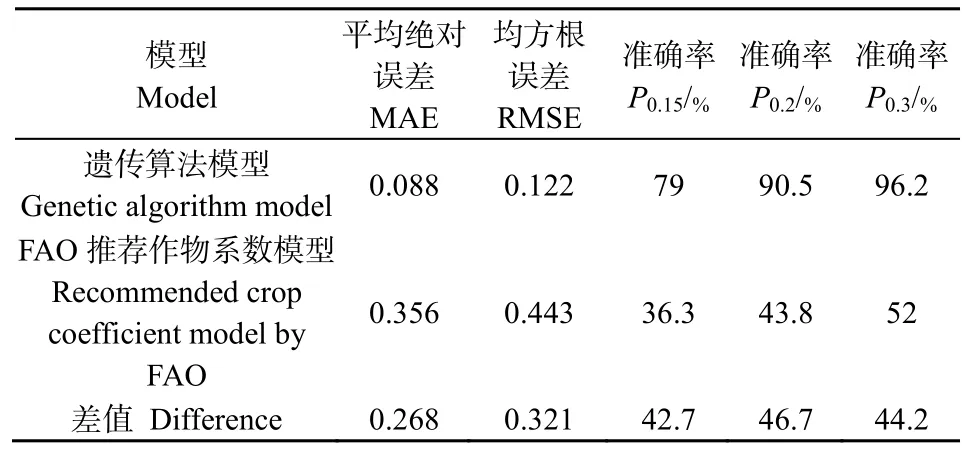
表7 全生育期不同模型作物系数拟合精度值Table 7 Fitting precision values of crop coefficients of different models during the whole growth period
3.2.2 蒸散量的对比
绘制上述两种模型蒸散量模拟值与实际值的对比图,见图 5。结果表明,两种模型拟合的蒸散量变化趋势基本一致;FAO模型的误差在初期、发育期较小,在中期、后期逐渐增大;修正后的遗传算法模型,其模拟值更加接近实际值,究其原因,FAO推荐的夏玉米初期、中期、后期的作物系数分别为0.3、1.2、0.6,而本文根据实测数据拟合的初期、中期、后期作物系数分别为0.28、0.611、0.386,FAO推荐的作物系数除初期外明显偏高,进而高估了夏玉米的实际蒸散量;相比之下,本文利用遗传算法模型拟合的作物系数更加接近实际情况,且结合了复合函数对估算误差偏高的生育阶段进行优化,这使得本文模型对夏玉米蒸散量的估算误差更小,可满足一定的精度要求。全生育期内,修正遗传算法模型的平均绝对误差为0.893 mm·d−1,均方根误差为 1.284 mm·d−1,P4为 100%,r为 0.863;FAO推荐作物系数模型的平均绝对误差为 3.841 mm·d−1,均方根误差为 5.28 mm·d−1,P4为 58.1%,r为0.654。本文模型在拟合夏玉米作物系数、蒸散量方面均有较高精度,可用于夏玉米蒸散量估算。

图5 全生育期不同方法ET计算值与实际值比较Fig.5 Calculated ET compared with actual value based on different ways during the whole growth period
4 讨论
在无土壤水分胁迫条件下,作物系数是作物实际蒸散量与参考作物蒸散量的比值,其数值可反映出因作物种类差异、土壤水肥条件、作物生长发育状况等差异对农田蒸散量的影响(Alberto et al.,2014)。本文采用单作物系数法计算夏玉米实际作物系数,相比于双作物系数法,单作物系数法可使用较少的数据而得到较高精度的作物系数估计(曹永强等,2019)。本文将夏玉米全生育期划分为4个生长阶段,并利用无受旱胁迫的实测蒸散资料和同期气象数据,结合遗传算法得到无受旱胁迫下的玉米初期、中期和后期作物系数,根据叶面积指数和发育期天数构造修正模型,对误差较大的发育期作物系数进行调整,得到夏玉米各生长阶段的作物系数估算值,进一步可估算夏玉米的蒸散量。
由本文模型得到的夏玉米作物系数,全生育期呈现出先增后降的变动趋势,这与肖然等(2019)的研究结果相一致,且估算蒸散量的平均绝对误差小于1 mm·d−1,模拟效果较好。进一步将该模型与FAO推荐作物系数模型进行对比,在估算蒸散量方面,FAO推荐作物系数模型在初期的估算误差较小,中期、后期估算误差较大;而本文模型的估算值更加符合实际蒸散量。一方面,在生长初期,玉米植株矮小,叶片不发达,农田蒸散量主要来自于土壤蒸散,植株蒸腾占比很少,且总蒸散量很小,所以在生长初期,无论哪种模型的估算误差都较小;到发育期,随着光热条件逐渐充足,玉米生长发育迅速,叶片快速伸展,由于在中期、后期,FAO推荐的作物系数值偏大,故从该阶段开始,FAO推荐作物系数模型的估算误差开始增大,而本文模型借助复合函数对算法输出的作物系数进行了修正,缩小了误差,优势得以体现;到中期和后期,FAO推荐的作物系数明显偏高,使得蒸散量估算误差进一步增大,而本文模型立足于实测资料,对蒸散量估算的均方根误差小于1.5 mm·d−1,可满足一定的精度要求,可作为估算夏玉米蒸散量的一种方法。另一方面,FAO推荐的作物系数值是针对于作物生长阶段均无水分胁迫、耕作和田间水分管理条件良好,作物能获得最大收成时的值,而作物实际生长状况会受多种因素干扰,这就使得FAO推荐的值会高于实际值,从而增大了误差(袁宏伟等,2018)。
本文修正遗传算法模型对夏玉米蒸散量的估算误差可满足一定的精度要求,不失为一种估算夏玉米蒸散量的新思路,但本文计算是基于地下水埋深为1 m的砂姜黑土实测数据,由于不同土质、不同地下水埋深会对作物系数产生不同的影响,不同作物的生长发育状况也不尽相同,故基于不同土质、不同地下水埋深、不同作物生长情况下的蒸散量估算需进一步研究。
5 结论
(1)本文构建了基于遗传算法的夏玉米蒸散估算模型,并利用叶面积指数构造修正模型,对发育期作物系数进行数值修正,模型对夏玉米全生育期作物系数的拟合、预测精度均较高。根据修正遗传算法模型,训练集中作物系数模拟值与实际值的MAE为0.083,RMSE为0.112,P0.3为97.3%;检验集中两者MAE为0.101,RMSE为0.805,P0.3为93.5%。本文模型可以提高作物系数的计算精度,可用于夏玉米作物系数的模拟。
(2)基于修正模型得到的夏玉米蒸散量计算精度较高。训练集中蒸散量模拟值与实际值的 MAE为 0.786 mm·d−1,RMSE 为 1.120 mm·d−1,r为 0.898;检验集中两者MAE为1.148 mm·d−1,RMSE为1.610 mm·d−1,r为0.813,蒸散量的拟合精度均高于 FAO推荐作物系数模型。
(3)与FAO推荐作物系数模型相比,全生育期内,修正遗传算法模型作物系数和蒸散量的拟合误差、准确率均有明显提高;对全生育期内逐日作物系数与蒸散量的计算,本文提出的修正遗传算法模型模拟精度符合精度要求。
