基于线性二次型调节器的乒乓舵最优控制方法

李 旭，霍鹏飞，陈 超，雷泷杰

(西安机电信息技术研究所，陕西 西安 710065)

0 引言

随着科技的发展，现代战争的模式发生了巨大的变化。“外科手术式精确打击”与“斩首行动”等作战思想的运用，对精确制导武器提出了越来越高的要求。低成本弹道修正技术在提高武器作战性能，节约成本方面有明显优势，弹道修正引信可以使传统库存无控弹药灵巧化，有着成本低、响应时间快、后勤负担小、附带毁伤低、效费比高等一系列优点，采用弹道修正引信进行无控弹丸精确化改造思想已深入人心。据统计，具备弹道修正技术的弹药，其杀伤成本相对于精确制导弹药而言降低了26～28倍，而同样毁伤概率下可以减少普通弹药消耗量的90%[1]。二维弹道修正引信分为固定翼和整体减旋可动翼两种方案。各国在可动翼二维弹道修正引信的研究中，通常采用鸭式气动布局，引信利用弹丸原有的飞行稳定性简化控制系统设计。这种方案中，弹丸发射后引信通过减旋机构，确保弹体保持原有旋转状态，而引信相对于弹体整体减旋。引信上通常安装有一对同向升力翼来提供修正力及力矩，一对差动可动翼来控制引信滚转角，以此来调节修正力的方向[2-3]。

舵机作为二维弹道修正引信的执行机构，带动一对差动可动翼进行引信滚转角控制。由于舵机需要在匹配滚转控制指令周期下，达到运动误差的要求。舵机中存在电感这类储能元件会因为电流的剧变产生延时，且测量会产生误差，这对舵机自身控制周期的稳定性提出了较高要求，指标要求为换向频率不小于50 Hz，频率变化率不超过±2.5%。对于二维修正引信使用乒乓舵机的控制问题，国内外资料提及较少，并且不涉及具体控制器设计方法。本文针对上述问题，提出了基于LQR控制算法的舵机控制系统。

1 乒乓舵机数学模型及线性二次型调节器(LQR)控制算法

1.1 乒乓舵机的数学模型

乒乓舵机由脉宽调制信号驱动音圈电机运动，经铰链式传动装置带动差动翼面运动，翼面运动极限位置有机械限位，形成乒乓舵[4]。乒乓舵结构示意图如图1所示。

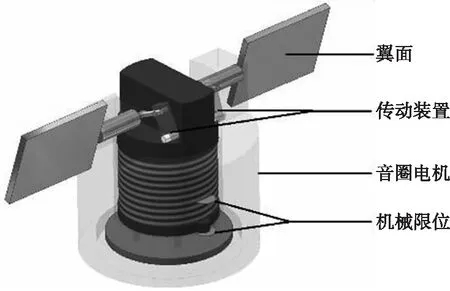
图1 乒乓舵机结构示意图Fig.1 Structure diagram of electrical actuator

在磁场作用下，通电导体切割磁力线产生反电动势，其大小可以表示为：

E=δBlcv=kEv

(1)

式(1)中，E为反电动势，δ为电磁感性系数，B为磁场强度，lc为线圈导线长度，v为动子的运动速度，反电动势常数kE=δBlc。

当音圈电机线圈绕组两端存在电压，使音圈电机处于运动状态，此时音圈电机线圈回路的动态电压平衡方程式为：

(2)

式(2)中，u为线圈绕组两端电压，L为线圈绕组电感，i为流过线圈电流，R为线圈阻值。

根据音圈电机工作原理及实际工作条件可知，电机动子上有电磁力F、惯性力Fm、摩擦力Fc和负载力Fl。其关系表达式为：

F=Fm+Fc+Fl

(3)

当线圈中电流为i，磁场强度为B，导体会受到电磁力的作用，其大小为：

F=δBlci=kfi

(4)

式(4)中，电机力常数kf=δBlc。

惯性力Fm表达式为：

(5)

式(5)中，m为动子部分总质量，a为动子运动加速度，x为动子运动行程。

动子运动过程中，其运动速度表达式为：

(6)

由于音圈电机的粘性摩擦力远大于干摩擦力，所以只考虑粘性摩擦力，其表达式为：

(7)

式(7)中，c为粘性阻尼系数。

负载力由舵机翼面的铰链力矩Mh产生，其表达式为：

(8)

式(8)中，l为力臂。

联立式(3)—(5)、(7)和(8)，则乒乓舵机的力平衡方程为：

(9)

考虑到电机运动过程中的行程误差，其表达式为：

e=x-xc

(10)

式(10)中，xc为电机运动总行程。

联立音圈电机的动态电压方程式(2)、力平衡方程式(9)、速度方程式(6)及误差方程式(10)，乒乓舵机动力学方程组如式(11)所示[5-6]。

(11)

1.2 线性二次型调节器控制算法

线性二次型调节器控制问题属于二次型性能指标的最优控制问题，其实际上是要用最小的控制量来获得最小误差的最优控制。由LQR控制原理可知，对于形如式(12)中描述的线性系统，选择最优控制输入，使得式(14)中所描述的性能指标J最小。

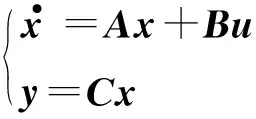
(12)

u*(t)=-K*x(t)

(13)

(14)

式(14)中，Q为半正定矩阵，R为正定矩阵。该指标的物理意义在于设计控制变量u，使用最少的能量，使得状态x在整个控制过程中最小。反馈矩阵K*可通过式(15)计算。

K*(t)=-R-1BTP

(15)

式(15)中，P为Riccati代数方程(16)的解[7]。

ATP+PA-PBR-1BTP+Q=0

(16)

2 基于线性二次型调节器控制算法的乒乓舵机控制方法

将乒乓舵机动力学数学模型写成状态空间描述的形式。

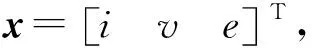
(17)

选取的三种状态变量中，i和e均可测，e通过微分及低通滤波得到v，则对于状态空间方程(17)中描述的线性系统，可以得到式(18)所示的输出方程。则式(17)和(18)一起构成形如式(12)的乒乓舵机运动的状态空间描述。

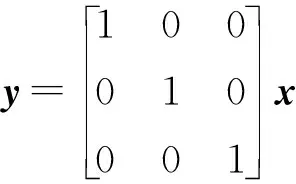
(18)

对于乒乓舵机的线性系统而言，选取R=[a](a>0)，Q为半正定对角阵,则A、B、Q、R均为常数矩阵，P(t)存在且唯一，并且为非负定。同时系统输入u不受约束。满足LQR控制算法的应用条件[8-9]。

应用LQR控制算法得到式(19)中的最优控制律。

(19)

3 仿真验证

根据上一章得到的乒乓舵机控制系统数学模型及最优控制律，运用Matlab中Simulink工具箱建立乒乓舵机控制系统模型，如图2所示。

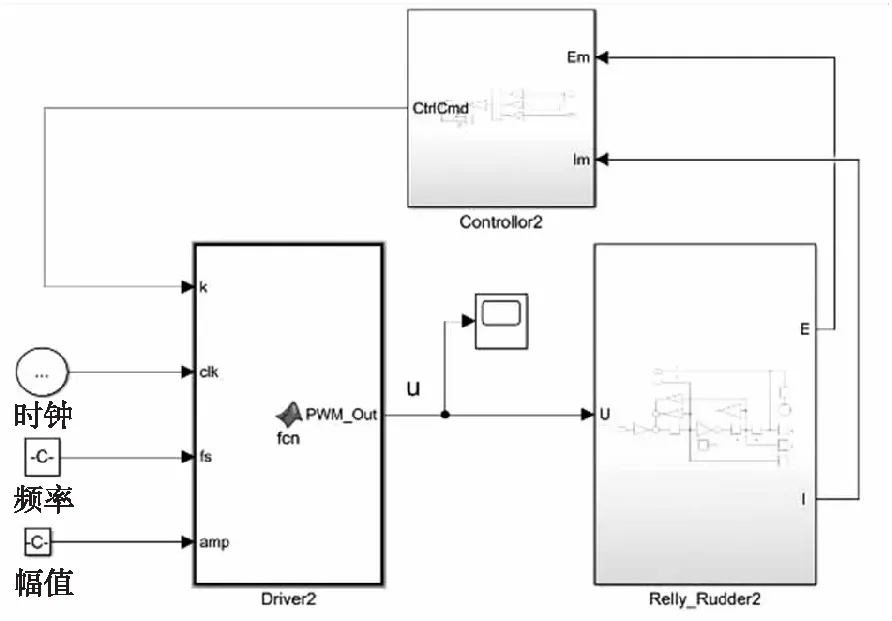
图2 乒乓舵机控制系统仿真图Fig.2 Simulink diagram of electrical actuator control system

为了验证基于LQR控制算法的乒乓舵控制方法的控制效果，在不引入测量误差的情况下，控制系统的仿真结果如图3所示。

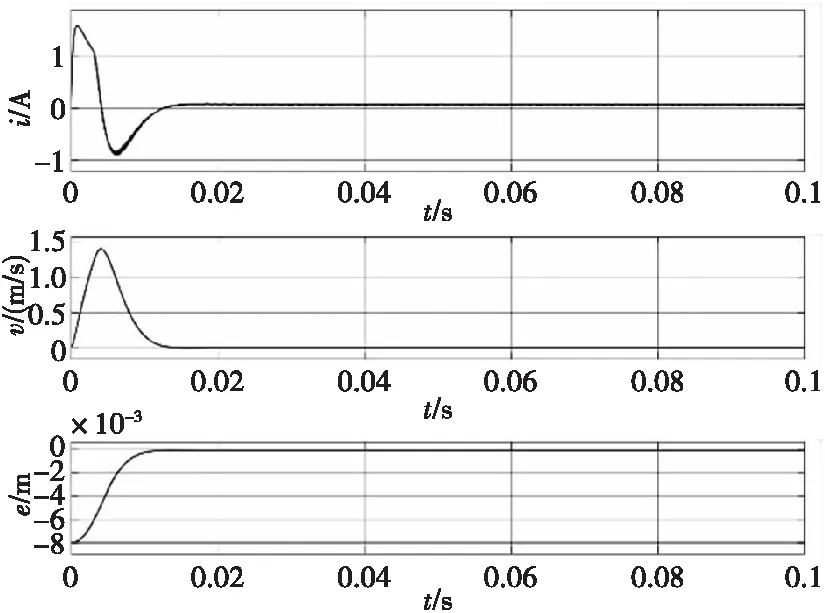
图3 乒乓舵机控制系统电流、速度及行程误差变化曲线Fig.3 Current, speed and distance error diagram of electrical actuator control system

速度估计值与理论值差别如图4所示。由图4可以看出，速度的估计值迅速收敛至理论值。

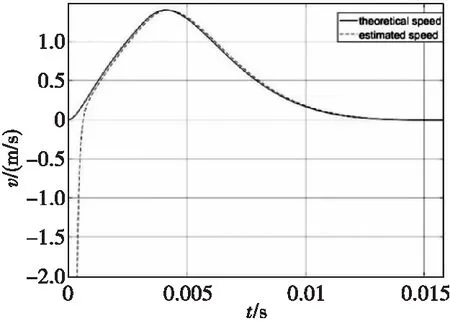
图4 乒乓舵机运动速度理论值与实际值变化曲线Fig.4 Actual value and ideal value of movement speed diagram of electrical actuator

由图3的仿真结果中可以看出，调节时间ts≈10 ms，超调量为0。同时线圈电流，动子运动速度以及行程误差变化平缓，其中线圈电流、动子速度及行程误差均趋向于0。所需控制量很小，仿真结果如图5所示。使用乒乓舵三环PID算法的调节时间ts≈42 ms，且存在25%的超调量。同时可以看出，LQR较PID算法可节省约39%的功耗，仿真结果如图6所示。LQR控制算法与PID控制算法控制仿真结果对比如图7所示。

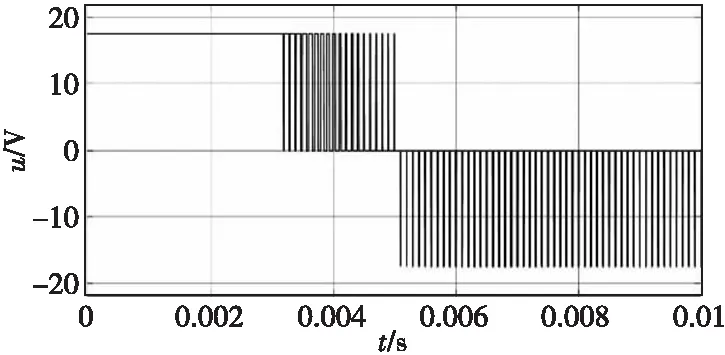
图5 乒乓舵机控制系统控制量变化曲线Fig.5 Voltage diagram of electrical actuator control system

图6 LQR与PID控制算法瞬时功耗仿真结果Fig.6 Power consumption diagram of LQR and PID algorithm

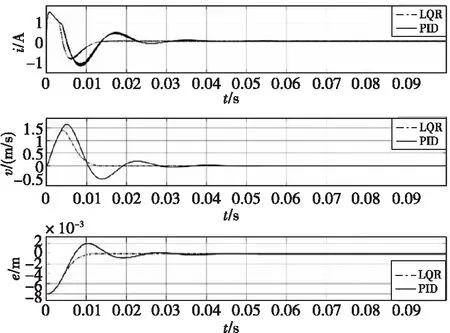
图7 LQR控制算法与PID控制算法仿真结果Fig.7 Simulation results diagram of LQR and PID algorithm

当行程误差引入均值为0 mm，方差为0.001 mm的正态误差，电流引入均值为0 mA,方差为20 mA的正态误差时，单次换向时间ts≈9.86 ms，变化率1.4%，满足换向频率不小于50 Hz，频率变化率不超过±2.5%的指标要求。测量误关如图8所示。

图8 引入电流和行程误差的测量误差曲线Fig.8 Measure error diagram of current and distant error

对稳定状态的控制结果进行统计分析可知，乒乓舵机控制中，电流存在均值为83.4 mA，均方差为325.1 mA的误差；速度存在均值为-0.002 m/s，均方差为0.078 m/s的误差；行程误差存在均值为-0.14 mm，均方差为0.13 mm的误差。三环PID控制中，电流存在均值为63.6 mA，均方差为460 mA的误差；速度存在均值为-0.01 m/s，均方差为0.092 m/s的误差；行程误差存在均值为-0.21 mm，均方差为0.33 mm的误差。仿真结果对比如图9所示。

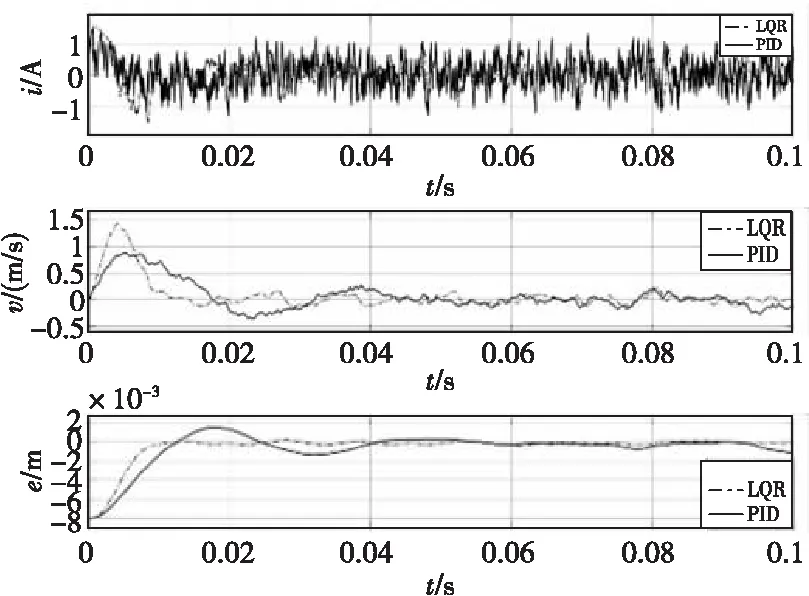
图9 引入测量误差时LQR与PID控制算法仿真曲线Fig.9 Simulation results diagram of LQR and PID algorithm with measuring error

基于最优控制理论中LQR控制算法的乒乓舵机控制方法与传统的三环PID控制算法相比，其调节时间短，不存在超调，控制精度高，同时所需控制量少。其设计方法简单，仅需要判断系统是否存在一个最优控制律使其达到稳态时，使式(14)中的性能指标最小。在满足LQR控制算法应用条件的基础上求解Riccati代数方程，求得P阵，利用式(16)便可得到使得式(15)中性能指标最小的最优控制律。

4 结论

本文提出基于LQR控制算法的乒乓舵机控制方法。该方法先建立乒乓舵机数学模型，然后将乒乓舵机动力学数学模型写成状态空间描述的形式，再判断乒乓舵机的状态空间描述是否满足LQR控制算法的应用条件，最后应用LQR控制算法得到最优控制律。其设计方法简单，不需要将乒乓舵机控制器分为多级回路进行单独设计。由仿真结果可知，基于LQR控制算法的乒乓舵机控制方法与传统的三环PID控制算法相比，其调节时间短，不存在超调，控制精度高，同时所需控制量少。由于LQR控制算法对系统建模准确度要求较高，在实际使用过程中，易产生控制误差散布较大的情况，故在工程应用中应考虑增加滤波。