小学高年级数学问题解决能力的养成路径
2021-03-09吴志远
摘 要:数学问题解决是培养学生数学学科素养的有效途径,也是增强学生学以致用意识的重要目标。实践中,作者结合“行程问题”,指导学生掌握问题解决的一般思路,使他们在问题解决中提高数学推理、逻辑思维等综合能力。文章通过对学生展开“行程问题”的测试分析,梳理问题解决存在的共性问题,探究其成因,提出改进教学的策略和建议。
关键词:小学高年级;数学课程;问题解决能力
中图分类号:G427 文献标识码:A 文章编号:2095-624X(2021)52-0067-03
作者简介:吴志远(1990.3—),男,江苏省常州市武进区实验小学,中小学二级教师,本科學历。
引 言
数学问题解决考查的是学生创造性地利用数学知识解决实际问题的能力。数学课程具有逻辑性、抽象性的特点。在解决数学问题的过程中,学生需要深入领会题意,抓住问题表征,转换解题思路。面对不同的数学问题,小学生需要掌握画图、转化、替换、数形结合等解题策略。“行程问题”题型多样,是小学数学教学的重难点。笔者结合高年级数学的“行程问题”,从问题解决的教学中,提炼和梳理解题的方法和技巧,使学生能够从问题解决中,拓展数学逻辑思维,提高问题解决能力。
一、对“行程问题”测试结果的分析
“行程问题”的测试,旨在调查学生面对“行程问题”时出现的常见错误,为教师改进教学策略提供参考依据。笔者在本次测试中发放问卷50份,回收有效问卷47份,有效率为94%。测试结果基本能够包含学生在面对“行程问题”时出现解题错误的大部分情况。
(一)测试题型分析
在本次“行程问题”测试中,笔者专门选取多种题型,以便了解学生的常见错误。第一题,典型的相遇问题。该题给出速度、时间,求解路程,主要考查学生对“行程问题”的基本掌握情况。第二题,环形跑道问题。该题将传统的直线追赶,转换为环形跑道,增强学生对数学变式的理解。第三题,没有路程,只给速度,求相遇时间。该题着重考查学生的审题、读题能力,要求学生在题目中找出等量关系。第四题,不同时出发问题,即给出总路程、各自速度,着重考查学生的分析问题能力。第五题,给出总路程、时间,求某一速度。该题考查学生运用方程来解决问题的能力。第六题,未相遇问题。该题难度较高,着重考查学生分析题意和提炼等量关系的能力。第七题,追击问题。题目难度更大,在同时出发后,经过某一时间,给出距离,求解该段时间。该题考查学生能否引入线段图来分析题意,找出等量关系。
(二)常见错误类型分析
在本次测试中,笔者对学生出现的错误进行了整理分析。总的来说,第一题,出错人数为14人,出错率为29.79%。错误表现:学生计算错误,找不准等量关系,解题格式不规范等。第二题,出错人数为15人,出错率为31.91%。错误表现:学生对环形跑道理解不当,找不出等量关系,计算错误,对速度的倍数关系理解错误等。第三题,出错人数为12人,出错率为25.53%。错误表现:学生列不出等量关系,对速度求解错误,忘记速度乘时间等于路程,对题目中的路线不明晰等。第四题,出错人数为26人,出错率为55.32%。错误表现:学生计算错误,对“慢车先出发1小时”理解不清,解题错误等。第五题,出错人数为34人,出错率为72.34%。错误表现:学生使用数据单位不统一,对速度求解不正确,题意不明晰,找不出等量关系等。第六题,出错人数为27人,出错率为57.45%。错误表现:学生对“相距121千米”不理解,对行车路线搞混,未能辨析路程、速度、时间三种关系,没有理清解题思路等。第七题,出错人数为39人,出错率为82.98%。错误表现:学生找不准等量关系,不清楚行车路线,不理解追击问题,解题思路不清晰等。
二、造成“行程问题”解题错误的成因归纳
从小学生“行程问题”测试结果来看,造成学生解题错误的原因很多,与教师、学生都有关系。
(一)教师方面
在“行程问题”教学中,教师自身存在一些误解,部分教师将“问题解决”归结为解数学题,要求学生熟记公式、定律,多做题,多训练,提高解题速度和正确率。但教师死记硬背式的教学思路,导致学生并不能真正理解题目[1]。同时,“行程问题”变式形式多样,有相遇问题、追击问题,还有背向运动问题等,有直线运动,还有环形运动。基础较差的学生,对基本的路程与速度、时间的等量关系理解不清楚,缺乏灵活应用的能力。在分析题意时,学生易犯找不出等量关系的错误。例如,两地相距240 km,两车同时从两端相向开出,3 h后相遇,一车速度为38 km/h,另一车速度是多少?在解题时,部分学生将路程与速度概念混淆,得出240-38=202 km/h。部分学生在解题时,方程列式不正确,还有部分学生不会利用线段图辅助分析题意,找不出等量关系。教师在讲解基础知识点时,对“问题解决”多停留于表层,忽视对学生的解题思路进行启发。这导致学生对数学问题感知不深,影响解题能力的提高。
(二)学生方面
在“行程问题”测试结果的分析中,学生对该类问题的求解错误多集中在以下几个方面。一是数学基础薄弱,计算过程中出错。部分学生对数学算理、算法缺乏理解,在面对“行程问题”时,混淆时间、速度之间的关系,对“相遇”理解不准确,甚至对两位数乘三位数,两位数乘两位数的积也计算不出,存在计算错误。二是学生对解决数学实际问题缺乏经验。在“行程问题”测试中,与“相遇”相关的题意,部分学生感到陌生,理解不深刻,对问题情境缺乏亲身体验,影响解题思路。三是分不清等量关系。对“行程问题”的求解,学生需要透析题意,梳理已知、未知条件,找出关键信息,以及隐藏信息。例如,在“两车还相距120千米”的题中,部分学生感到困惑,不明白是相距“120”千米,还是相遇后又相距“120”千米。四是对“行程问题”的变式理解不到位。与行程相关的实际问题,涉及的变式情况较多,部分学生受思维定式的影响,总是生搬硬套来解题。对题意辨析不清,如学生对“相向”“相背”“同时”等关键词理解不到位,导致解题出错。五是缺乏独立思考力。部分学生在面对“行程问题”时,总是依赖他人,总要将自己的解题方法与他人对照,不善于独立解决问题。
三、提高学生问题解决能力的有效建议
(一)教师要善用模拟实践方法,让学生体会
“行程问题”
在“行程问题”相关知识点的讲解中,如果教师单纯讲解“相遇”的几种情形,那么学生就容易混淆,理不清解题思路和解题方法。如果学生就有了直观的体验,对“行程”相关的问题就会理解得更深刻。模拟实践法,就是以学生参与演练的方式,去创设“行程”问题的情境。相遇问题通常有三种类型:第一种,甲、乙的速度给出,相遇时间给出,来计算甲乙相距距离。第二种,甲、乙速度给出,相距距离给出,求相遇时间。第三种,甲、乙相距距离给出,甲的速度和相遇时间给出,求乙的速度。教师可以利用多媒体,以动态直观的方式来呈现不同条件下的相遇问题,指导学生理解题意,分析所遇题目属于哪种类型的“行程问题”。同样,模拟实践教学法强调学生的主体性,注重以学生体验“行程问题”的方式,让学生感知“相遇”的不同情形。例如,某题中,父子两人郊游,爸爸让儿子先走十步,接着爸爸再出发,爸爸走3步的时间,儿子可以走5步,爸爸走9步的距离,儿子需要走17步。问爸爸走多少步可以追上儿子?对该题解题思路的探讨,教师可以让学生扮演父子,分别按照如上的条件来绘制父子的运动线路图。在小组合作体验中,学生能够对“追击”问题理解得更深刻,也有利于掌握“行程问题”的求解方法。
(二)重视“行程问题”概念的剖析,巩固学生数学理解力
“行程问题”的问题情形较多,学生对“路程、速度、时间”等概念理解存在偏差。基于此,教师要重视基本算理、算法的讲解,特别是对基本概念的剖析,以增强学生对三个量的深刻认识[2]。“行程问题”涉及的数量可以是整数,也可以是小数,还可以是分数;涉及的运动情况,可以是单个物体,可以是两个物体,还可以是三个及以上物体;涉及的运动方向,可以是同向运动,也可以是相向运动,还可以是背向运动。面对基本的数量关系,如“速度×时间=路程”“路程÷速度=时间”“路程÷时间=速度”等,教师要引导学生从题意剖析中找出等量关系。
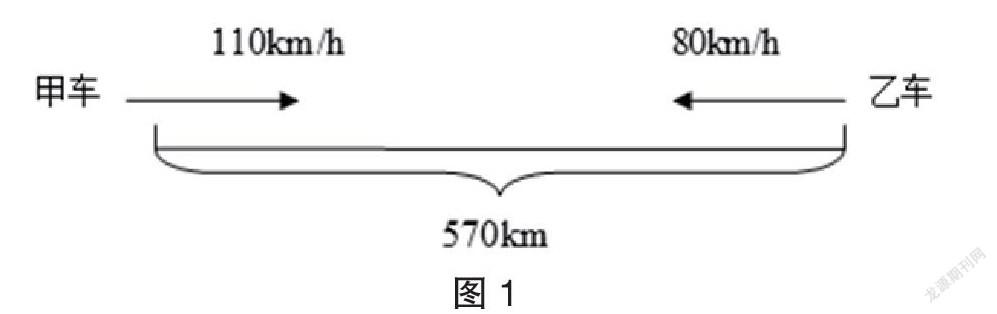
例如,某题中,两地相距570 km,有甲乙两辆汽车,速度分别为110 km/h、80 km/h,同时相向开出,问几个小时两车相遇?对该题的讲解,教师应先指明此为“行程问题”中的“相遇问题”,引导学生找出题目中的已知条件及隐藏的关键信息。题目给出甲车的速度、乙车的速度,两地的总距离。两辆车相向而行,“相遇”的关键信息是“两车共同走完了该段路程”,如图1所示。
由此,教师可以引导学生思考,根据“相遇”还能够提取哪些关键信息。部分学生想到“两辆车行驶的时间是一样的”。部分学生认为,甲车的行驶速度、行驶时间所得的路程,与乙车的行驶速度、行驶时间所得的路程之和,正好等于这段距离。也就是说,假设相遇时间为x,则等式方程为:110x+80x=570,求解得到x=3。在该题的求解过程中,教师要让学生认识到两辆车所行驶的距离之和正好为该段路程。这种教学方式可以使学生深刻体会“路程=速度×时间”的意义。教师通过启发学生的数学思维,采用灵活的教学方式,能够让学生准确把握“行程问题”的解题要点。
(三)注重数形结合,增强学生解题反思能力
教师可以对“行程问题”展开变式训练,特别是依托数形结合思想,让抽象的“行程问题”变得具体、简洁[3]。线段图画法能够帮助学生从题意中梳理已知、未知条件,找准等量关系,为正确解题提供参考。
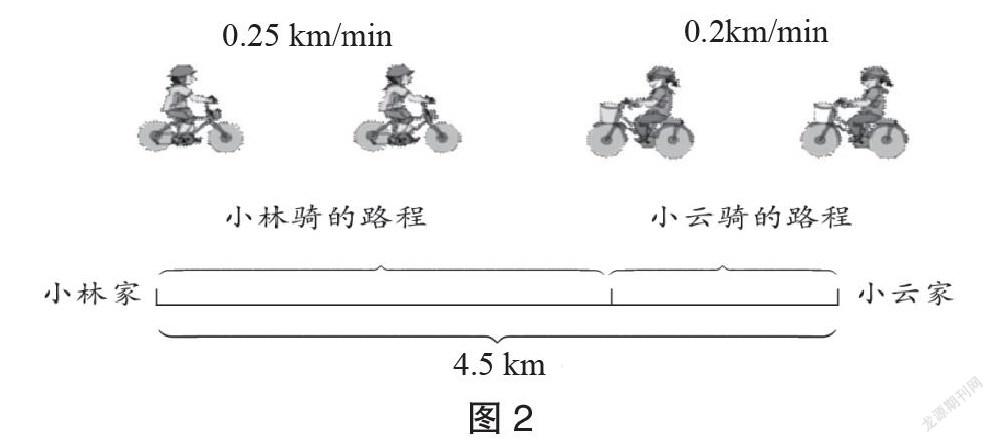
例如,某题中,小林与小云相距4.5 km,小林骑车速度为0.25 km/min;小云骑车速度为0.2 km/min。问两人何时相遇?教师在分析讲解该题目时,要引导学生理解“相遇”的意思。结合两人相距的距离,两人同时出发,相向而行,相遇时,正好将该距离走完,即两人相遇时,各自所走的距离之和,等于两人相距的4.5 km,如图2所示。
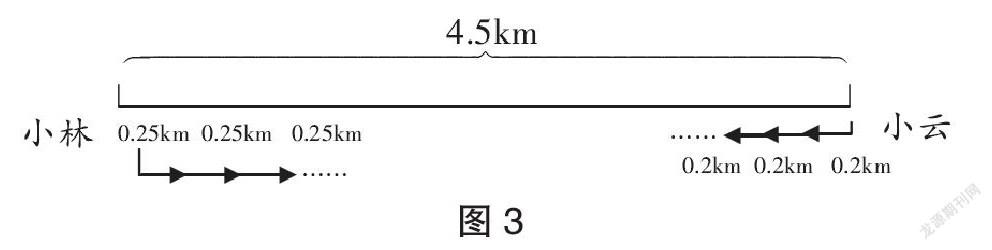
教师以画图的方式,对两人骑车相向而行的过程进行直观呈现。学生仔细观看小林、小云的行驶时间,能够发现相遇时,两人刚好走完全程。这时,教师可以引入问题:小林的骑车路程与小云的骑车路程之和是否等于总路程?请学生思考,能否求出小林的行驶路程和小云的行驶路程。部分学生认为“不能求出”,因为不知道他们各自行驶的时间是多少。但部分学生发现,两人的行驶时间是一样的,因为是同时出发,所以相遇时两人所走的时间是一样的。那么,如何列方程来求解?教师可以鼓励学生进行小组讨论,并对各组的想法进行展示。教师可以引导学生思考,在本题中,小林和小云相向而行,一分钟后,他们共走了多少千米?如图3所示。
学生通过思考后得到“0.25+0.2=0.45(千米)”。教师让学生再思考,再经过1分钟,他们共走多少千米;第5分钟时,他们共走多少千米;他们共走多少分钟,才能走完0.45千米。由此得到“(小林的速度+小云的速度)×相遇时间=路程和”。通过引入线段图的方法,教师能够让学生在面对“行程问题”时,体会到数形结合思想的简洁美,让其快速找准等量关系,提高数学问题解决能力。
结 语
对于“行程问题”的探究,教师与其直接给学生解题公式,不如引领学生共同参与探索,特别是鼓励学生在面对“行程问题”时,说出自己的想法,鼓励学生质疑。教师要善于抓住契机,激发学生主动思考数学的“行程问题”,调动学生的学习能动性。教师在讲解“行程问题”时,要注意三点。一是联系学生实际,让学生亲历“相遇”情境。二是引导学生找准关键信息,特别是准确理解题意。三是注重数形结合,利用线段图来梳理数量关系。对于“行程问题”,教师要注重一题多变,多总结解题方法,让学生抓住解题的关键点。
[参考文献]
高建军.小学高年级学生数学问题解决能力的培养路径探究[J].当代教研论丛,2020(03):83.
马淑芳.小学高年级数学解决问题能力的培养路径探究[J].试题与研究,2020(03):84.
尤麗萍.小学高年级数学问题解决能力的培养路径探究[J].新教师,2019(01):62-63.
2658501705313
