船用变风量系统风管动态模型的建立与检验

王陈强

摘 要：本文采用机理建模的方法，建立了一套用于某船舶的变风量系统研究的风管网络动态模型。同时，提出了一种管路沿程阻力系数计算的迭代方法，一种“阻力平衡计算”的建模方法，以及模型正确性的检验方法，对于模拟变风量系统和研究变风量控制系统具有借鉴意义。

关键词：船舶空调;变风量系统;建模;风管网络

中图分类号：U667.9          文献标识码：A            文章编号：1006—7973（2021）09-0116-03

由于船舶航行时航向的变化，船舱房间的热负荷特征变得更为复杂，同时海上多处于潮湿的气候环境，再加上船内空间的限制，船上的空调系统明显不同于陆地常规空调系统。一套调节快速的高静压变风量系统将很好地解决上述变化带来的问题，而对于这方面的研究却鲜有文献涉及。

变风量系统在陆地现代建筑中逐渐普及，李锐[1]等通过具体案例介绍了采用静压复得法在进行变风量送风管设计时应用，该方法存在计算工作量大的缺点。Shengwei Wang [2]总结了建立风管数学模型时需要考虑的三方面内容：管内摩擦阻力和局部阻力的计算，空气在管路中传递的延迟，在运输过程中与外界的热交换。张弢[3]也提出了与Shengwei Wang类似的观点;Wu Chen[4]等对风管网络的建模进行了简化：将风管网络当作并联管路处理;考虑风管的沿程阻力，但将局部阻力均设置为固定值。Ahmed Tukur[5]等提出用统计的方法，在已有的测量数据的基础上，建立风阀开度与阻力损失之间的关系。丁帅[6]等通过实验的方法，研究风阀开度和风机频率对主管和支管静压的影响，并得到了静压变化的规律。华宇剑[7]等对送风管网阻力特性分析，提出了送风系统阻抗-流量平衡模型。结合上述文献，本文以船用变风量系统为研究对象，从风管网络的阻力计算出发，建立起了一套可用于研究的动态模型。

1变风量系统风管动态模型的建立

1.1 研究对象说明

本课题的研究依托于某船舶变风量系统，系统的原理图如图1所示，新回风在空调箱中混合进行处理之后，送入静压箱，静压箱的出口为四路管径相同的保温圆风管，连接至房间内的变风量末端（VAV Box），并在走廊回风口收集回风。本文着重讨论变风量系统风管网络（图中用粗线标出部分）的建模。

1.2 风管类型划分

对于图1风管网络进行分析后可知，连接静压箱的四根送风管具有相似的结构，其阻力的等效电路图均如图2所示。

其中，Rm为管路沿程阻力，Z为弯头阻力，为分流三通阻力，为末端风阀阻力;将相同下角标的阻力划入同一类计算，将提高计算效率;所以，对于风管做如下划分：Ⅰ型风管（），Ⅱ型风管（），Ⅲ型风管（）。

1.3 基本功能模块

1.3.1 沿程阻力计算

沿程阻力计算公式如（1）所示：

在沿程阻力系数计算时，利用公式（2）内的隐含条件计算得到沿程阻力系数的最小值，通过最小阻力系数生成一系列等间距点，代入式（2）得到管内空气流速的大致范围，再利用二分法迭代出精确的沿程阻力系数。管径为0.1m，管长为1m的风管，在风速为10m/s时，迭代的阻力系数和风速的变化如图3所示。

迭代计算到第10步时，得到沿程阻力系数为0.02445的风速为8.77m/s，而上一步的迭代结果为10.07m/s，所以对应阻力系数的范围位于这两次计算之间，为0.02425～0.02445;从第11步开始，采用二分法进行精确阻力系数的搜寻，到达第17步时，得到的风速为10.004m/s满足设定的误差要求，计算停止。

1.3.2 局部阻力计算

局部阻力按式（4）计算

对于弯头和变径分流三通的局部阻力系数，可以通过查阅相应的表格得到。而风阀的局部阻力系数，可通过公式[8]（5）计算：

其中，为风阀的局部阻力系数;h为风阀的相对开度;为风阀全开时的阻力系数，可通过实验或查表得到。

1.3.3 管路延迟时间

管路延迟时间通过式（6）计算

其中，S为管路截面积，m2;V为送风量，m3/s;

1.4 阻力平衡计算

管网内的总风量由空调箱的风机段确定，在静压箱的出口处进行分流，最后送入12个房间内，模型假设每个房间内的气压均一致，而对于并联管网，管网两端的压差必相等，所以需通过迭代，不断地调整管路内的风量，直到各管段的压差一致，风量调整的公式为（7）

其中，i为管路编号;为所有管路阻力的算数平均值;为所有管路风量的算数平均值。

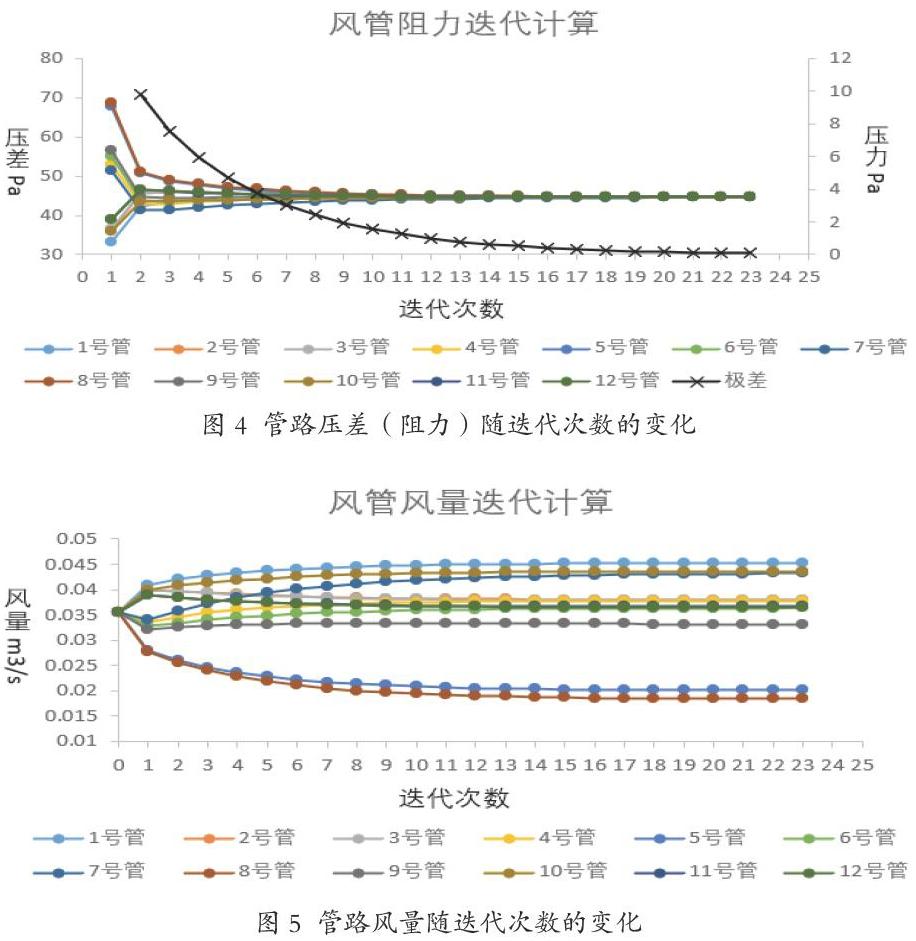
当总送风量为0.43m3/s时，管路迭代过程中阻力和风量的变化如图4和图5所示，在迭代至23步时，各管路阻力趋于一致，计算结束。可以看到，管路阻力的最大值和最小值之差（极差）呈现不断下降的趋势。而从图5中可以看出，随着迭代的进行，风管内风量大小趋于平稳。

1.5 动态计算实现

上述过程均是针对某一时刻的计算，风管内的风量大小根据风阀开度和风机频率的变化而实时的变化。在计算开始时，假设每根风管的风量大小是相等的，在经过数次迭代之后，得到每根风管的风量值，进行下一时刻的计算时，按上一时刻风量的分配比例计算初始迭代的风量值，可以加快收敛速度。

送风量的传递可以认为不存在延迟，但送风温度、湿度和浓度在管路中传递延迟不能忽略，通过定义由管路延迟时间控制长度的队列来存放送风参数，采用“队首存入，队尾取出”的方式达到模拟延迟的效果。

2 變风量系统风管动态模型的检验

2.1 风量单位阶跃响应

由于送风机的惯性作用，风机启动后各送风管的送风量变化如图6所示，通过检验风机运行到达稳定后各风管的风量大小验证模型的正确性。

2.2 送风温度阶跃响应

不考虑传感器惯性的情况下，初始温度为35℃时，送风温度随时间的变化如图7所示。由于管路的延迟，管路有各自的送风参数延迟时间;空气在经过空调箱换热器时出风温度随风量增大而升高，所以在排空管内原有空气之后得到了一个较低的送风温度，随着经过空调箱风量的提高，送风温度略有提升;最后所有管路的送风温度均稳定在一个相同的值。

3 结论

本文提出了一种应用于船舶变风量系统的风管网络动态模型的建立方法，可实现送风参数随时间动态变化，为研究变风量系统控制策略提供便利。

参考文献：

[1]李锐，赖学江， 厉美飞. 变风量空调系统的送风管管径及送风管静压的计算[J].制冷，2007（02）：77-80.

[2]Shengwei Wang， Dynamic simulation of building VAV air-conditioning system and evaluation of EMCS on-line control strategies， Building and Environment， Volume 34， Issue 6， 1999， Pages 681-705.

[3]张弢，张峻岭.变风量空调系统的数学模型[J].制冷与空调（四川），2008（02）：29-33.

[4]Wu Chen， Shiming Deng， Development of a dynamic model for a DX VAV air conditioning system， Energy Conversion and Management， Volume 47， Issues 18-19， 2006， Pages 2900-2924.

[5]Ahmed Tukur， Kevin P. Hallinan， Statistically informed static pressure control in multiple-zone VAV systems， Energy and Buildings， Volume 135， 2017， Pages 244-252.

[6]丁帅，孟庆龙，王博闻，谢安生，赵凡.变风量空调系统送风管道静压特性的试验研究[J].流体机械，2017，45（01）：66-71+59.

[7]华宇剑. 基于无中心的变风量空调送风系统模型与节能优化研究[D].西安建筑科技大学，2018.

[8]杨纪伟，张丽荣.调节阀阻力特性分析[J]. 閥门，2001（02）：22-24.