光电跟踪系统的模糊Ⅱ型控制技术研究

秦树旺,毛 耀*,包启亮

(1.中国科学院 光束控制重点实验室，成都610209；2.中国科学院 光电技术研究所，成都610209；3.中国科学院大学，北京100049)

引 言

光电伺服跟踪设备主要用于运动目标轨迹测量、航天器轨道确定、空间光束通信等领域，在军事和民用领域都有重要应用价值。随着被跟踪目标机动性提高、体积减小，对跟踪系统的反应速度和跟踪精度提出了更高要求，传统的控制方法需要革新[1]。

目前，应用最广泛的光电跟踪控制方法为多闭环反馈控制。该方法结构简单、鲁棒性强，结合经典比例-积分-微分(proportion-integral-differential,PID)控制，在已有的光电跟踪设备中得到成熟应用。然而PID方法下的系统型别低，动态响应速度有限，稳态精度不高[2]。

本文中提出一种控制方法，以此提高系统稳态精度。由自动控制原理可知，可以通过提高静态误差系数来减小稳态误差[3]。目前，在不影响系统稳定性的情况下，增大系统误差系数的措施有速度前馈复合控制[4]、目标速度预测控制[5]、速度滞后补偿等效复合控制[6]以及前向环路级联多重积分器[7]等方法。

前两种方法需要准确的目标运动模型，实际运行中很难实现；速度滞后补偿由于引入速度正反馈，使速度回路特性变软，精度提升能力有限。最后一种方法是在系统前向通路中增加积分环节，构成高型系统。其优点在于响应速度快，明显增大静态误差系数；然而积分环节的引入会使系统的动态品质变差，在跟踪误差较大的情况下容易引发积分饱和，给稳定性带来较大破坏。如果能根据系统状态动态地调整积分环节的数目或者增益，避免积分饱和，并且抑制型别升高带来的震荡，就能实现提高稳态精度的目的。于是“动态高型”控制方法被提出，且在国外已经应用到实际系统当中，如美国的发射区经纬仪[8]，其跟踪范围与精度远超同时代其它经纬仪设备。

国外有关此方法的研究文献极少，国内对动态高型技术的研究也进展缓慢。中国科学院长春光学精密机械与物理研究所的研究者们将动态高型方法引入到国内，并做了一些工作，构建出基本的动态高型模型[9-11]。然而动态高型方法存在两个难题：型别切换的时机判断问题、积分引入带来的抖动问题，用传统的方法很难解决。近年来，模糊控制方法被广泛应用于智能控制领域，经调研发现，模糊逻辑的特性可以弥补动态高型系统这两个缺陷，于是引入模糊控制器(fuzzy logic controller,FLC)与积分环节结合构成模糊Ⅱ型控制系统。参考文献[12]中对此方法做了初步尝试，虽然减小了稳态误差，但稳态信号噪声较大、实用性差，其原因主要在于对FLC的参量优化不足。

经典的FLC存在一些固有缺陷，如过分依赖专家经验、比例因子难以确定等。为了进一步提高模糊Ⅱ型控制器的性能，需要对模糊控制器进行参量优化。常用的优化方法有神经网络(artificial neural networks，ANN)、粒子群算法(particle swarm optimization,PSO)和遗传算法(genetic algorithm,GA)。ANN模拟人类大脑结构，存在学习收敛过程慢、网络结构难以确定并且易陷入局部极小值等问题[13]；PSO模拟群体生物相互协同寻优能力，属于随机的近似优化算法,主要应用于连续区域, 因此该算法存在早熟收敛和对离散性的问题难以应用的缺点[14]；GA模拟自然界生物种群的进化机制，通过迭代遗传得到最优参量，结构简明、收敛速度快，并且有多种方法可以对经典遗传算法(simple genetic algorithm,SGA)进行改良[15]。

本文中选用多种群遗传算法(multiple population genetic algorithm,MPGA)优化FLC的输入输出比例因子，避免了SGA早熟的问题，取得了优化效果。为了构造出经由MPGA优化的模糊Ⅱ型控制系统，本文中还根据系统状态动态改变积分环节增益，抑制型别升高带来的震荡，提高了系统稳态精度，对系统阶跃响应的综合品质也有一定改善。

1 高型控制系统

常用的光电跟踪控制方法为经典Ⅰ型双闭环反馈控制(double closed-loop control,DCLC)，如图1所示。图中,Gv为从快反镜实验平台中辨识所得数学模型，代表系统被控对象的传递函数，Cv为速度控制器，这两部分构成内环，称为速度环；速度环与位置控制器Cp串联构成外环，称为位置环。r,e,y分别表示参考输入信号、误差信号以及整个系统的输出信号。

Fig.1 Double closed-loop control

该系统全部环节的传递函数为:

(1)

式中，s为传递函数的参量，t为采样时间，a与k分别是内环与外环的增益，T1,T2,T3,T4是各个控制器传递函数的时间常数。

由于系统中有一个积分环节，所以是Ⅰ型系统。当系统稳态误差es(t)的绝对值小于输入信号值的2%时,视系统为稳定状态，其表达式如下：

(2)

式中,Kp,Kv,Ka分别为静态位置误差系数、速度误差系数和加速度误差系数，其表达式如下：

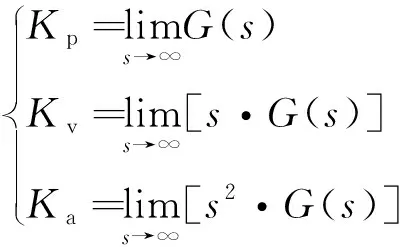
(3)

由(3)式可知，当系统型别升高，静态误差系数会提高，则稳态误差减小。在位置控制器之前并联一个积分环节，便可将系统变为Ⅱ型。然而系统型别升高会增大阶跃响应超调量，加剧系统震荡；随着积分环节增益变大，震荡会更大，在某些极端情况下甚至会达到积分饱和状态，使系统彻底失去稳定性。

为了解决上述问题，“动态高型”方法被提出。如图2所示，在前向通路中并联多个积分环节，根据系统误差状态判断积分环节的通断，动态改变系统的型别。然而有两个问题难以解决：(1)型别切换的标准没有定义,究竟要在什么时机提高型别，在何时降低型别，国内外的文献中没有给出理论指导;(2)型别切换瞬间带来的抖动难以消除。针对以上问题，研究者们给出了不同解决方法。

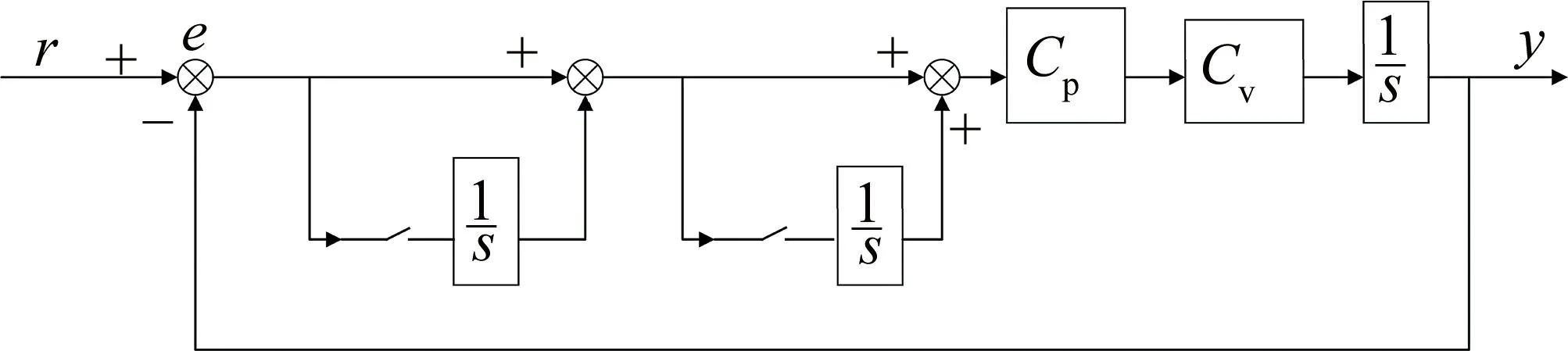
Fig.2 Dynamic high-order structure

参考文献[11]中在系统初始运行阶段，不并入积分环节，以防止积分饱和造成跟踪失败；而在平稳跟踪阶段并入积分环节，并且在跟踪误差较小时去掉积分环节。该方法提供了判断积分通断的规律，然而作者没有说明误差“大”“小”的判断标准，积分环节通断的控制方式也未说明。

为找到型别切换标准，参考文献[9]中通过反复实验试错得出误差阈值，高于该阈值就接入积分环节，低于该阈值断开。该方法在仿真实验中得到良好输出，但只能针对特定模型，不具有普适性，一旦换了实验平台就需要从头再来，费时费力。

参考文献[16]中提出了更通用的方法。通过判断误差e与误差变化率Δe的状态决定积分环节的通断。当e·Δe>0或Δe=0且e≠0时，并入积分环节；当e·Δe<0或e=0时去除积分环节。该方法取得了较好的仿真结果，但同样存在积分饱和的问题，因为该判断条件只注重误差与其变化率的符号变化而忽视了绝对值的影响，并且作者所用传统的PID控制器不易进行判断切换的操作。

在总结前人经验基础上，作者提出使用FLC解决上述问题。

2 模糊理论与模糊Ⅱ型控制器

模糊理论自20世纪50年代被ZADEH教授提出以来，经历几十年的发展，已经广泛应用于数学、控制、计算机等领域。模糊逻辑在分析问题时类似人脑逻辑，因具有一定的智能化，在当下具有广阔的应用前景[16]。

2.1 模糊控制器基本结构

模糊逻辑在控制领域的应用主要是模糊控制器，其经典结构如图3所示。包括4个步骤：(1)模糊化：将输入的精确量模糊化，为其分配隶属度函数和论域，便于进行模糊推理过程；(2)规则库：是FLC的核心部分，指导模糊推理的进行。传统规则库的建立依赖专家经验，规模太小模糊推理不够准确，规模太大会使计算时间过长，失去实用价值;(3)模糊推理：输入值经过模糊化以后，按照规则库的设定进行计算推理，得到模糊输出;(4)解模糊：将模糊输出精确化，是解模糊的反变换，类似于模/数与数/模过程。图中，u表示某部分的输出。

Fig.3 Classic FLC structure

2.2 FLC解决动态高型两个难题的原理

动态高型控制存在的两个难题如第1节中所述，模糊逻辑的特性可以解决这两个问题。

针对问题1：在系统运行过程中，积分环节的接入和断开会改变误差范围，人为设置的型别切换误差阈值就不再适用。传统的二值逻辑只能使用精确值作为输入，但在实际系统中误差值是一个范围，没有精确的理论指导，使得阈值难以确定。而FLC的输入量是一个范围，每一个误差可以用隶属度函数来表示它对整个系统性能影响的大小。如图4所示，横轴x表示输入误差，纵轴μ表示每一个误差所占的权重，是正态分布(高斯分布)。这种方式的优点是可以将全部的系统误差都考虑在内，而不必人为给定阈值，更具科学性和准确性。

针对问题2：通过设置合理的规则库及输出隶属

Fig.4 Membership function type

度函数，可得到变化的输出信号，以此作为积分环节的增益，将“积分开关型”转化为“增益变化型”，改突变为渐变。当增益为0时相当于积分断开，而随着误差的变化，积分环节的增益也动态变化，实时对系统进行调整，既增强了系统的动态反应能力，也消除了型别突变带来的抖动。

2.3 模糊Ⅱ型控制系统

FLC根据系统误差状态进行条件判断，经计算得出输出参量。本文中在经典的Ⅰ型双闭环反馈控制模型基础上，并入一个积分环节将系统变为Ⅱ型，引入一个FLC来控制积分环节的增益值，以此构成模糊Ⅱ型控制器，其结构如图5所示。

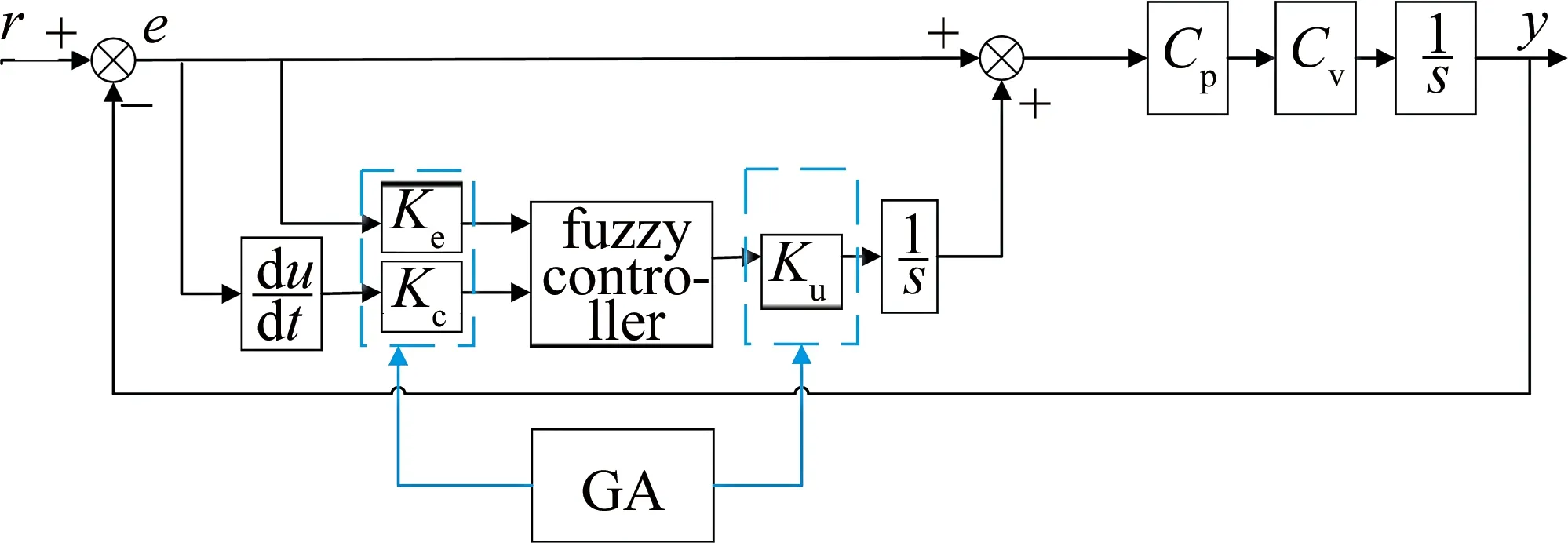
Fig.5 Fuzzy-Ⅱ control system

FLC为两输入单输出的Mamdani型，它结构简单，规则库设置方便，模糊推理过程可视，是最常用的FLC形式。输入变量为系统误差e及其变化率Δe，输出动态变化的k即为积分环节的增益。当k=0时表示积分环节断开，k>0时动态变化以实时调整系统状态。

规则库来源于专家经验，所以需要首先分析系统的状态及其对应的输入输出规律。当e·Δe>0时，误差绝对值有增大的趋势，此时应使k值较大，以迅速抑制误差；当e·Δe<0时，误差绝对值有减小的趋势，应适当减小积分增益以免矫枉过正。规则库的规模大对系统运行状态有很大影响。规模大，运行结果精确，但运行速度慢；规模小，运行速度快，但会忽略一部分条件。综合来看，本文中选用5×5的规则库，兼顾运行速度和精确度。

输入和输出的隶属度函数分布如图6所示。其中5个语言变量Nb，N，Z，P，Pb分别代表负大、负、零、正、正大，其论域要根据具体系统而定。输出隶属度函

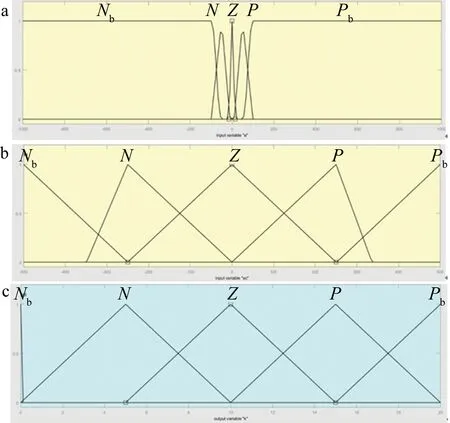
Fig.6 Membership function

数中Nb=0，代表积分环节断开，此时系统仍是Ⅰ型。规则库设置如表1所示，第1行表示误差e，第1列表示误差变化率Δe，中间表示积分增益k。

Table 1 Fuzzy control rules

图7为规则库的3维分布。x轴为e，y轴为Δe，z轴为k，从图中可以直观看出不同的输入量对应的输出量。然而，FLC由于过于依赖专家经验，往往难以达到最优状态，比如规则库的设定、隶属函数的形式和比例因子的大小等都难以确定。研究者们结合不同的智能算法对其进行优化，如引言部分所述。前面已经分析了误差e与误差变化率Δe与k值的关系，以此指导规则库的设计，同时可以据此确定隶属度函数分布；

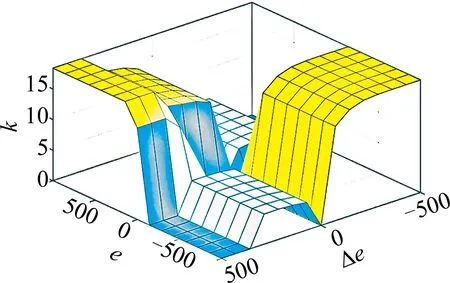
Fig.7 Rule base 3-D distribution

然而输入输出比例因子却无法由系统状态人为给定，所以经过综合比较本文中探索使用遗传算法对FLC的比例因子进行优化。

3 遗传算法

3.1 GA简介及早熟问题

遗传算法是由美国HOLLAND教授于1975年提出的一种高效的全局优化搜索算法，它的基本思想是基于达尔文的进化论和生物的遗传机制。在进行问题的求解时，将寻优参量编码成“染色体”的形式，经过选择、交叉和变异算子得到最优或次优个体[17]。然而，随着遗传算法的广泛应用以及研究的深入，其诸多缺陷与不足也暴露出来[18]。

其中，早熟问题是遗传算法中不可忽视的现象，主要表现在群体中的所有个体都趋于同一状态而停止进化，算法最终不能给出令人满意的解。原因主要在于这几个方面：超高适应度个体存在、交叉和变异概率固化、群体规模不合适以及终止判据不恰当等[19]。为了解决早熟问题，MPGA被提出。

3.2 多种群遗传算法

MPGA的运行流程如图8所示。在SGA的编码、选择、交叉、变异等步骤基础上，引入以下新元素[15]：(1)突破SGA仅靠单个群体进行遗传进化的框架，引入多个种群同时进行优化搜索；交叉概率和变异概率决定算法的全局搜索和局部搜索能力的均衡，对不同的种群赋以不同控制参量，以实现不同的搜索目的;(2)各个种群之间通过移民算子进行联系，其作用为将前一种群的最优值替换后一种群的最劣质，实现多种群的协同进化；最优解的获取是多个种群协同进化的综合结果;(3)通过人工选择算子保存各种群每个进化代中的最优个体，它们组成精华种群。精华种群和其它种群有很大不同，它不进行选择、交叉、变异等

Fig.8 MPGA running process

遗传操作，保证进化过程中各种群产生的最优个体不被破坏和丢失。同时，精华种群也是判断算法终止的依据，这里采用最优个体最少保持代数作为终止判据。这种判据充分利用了遗传算法在进化过程中的知识积累，较最大遗传代数判据更为合理。

3.3 MPGA设计流程

3.3.1 确定优化参量 遗传算法优化FLC有许多途径，可以优化规则库、隶属度函数、比例因子等参量[20]。通过实验对比发现，优化规则库或者隶属度函数计算量大，还不一定能得出满意结果，效率较低；优化比例因子算法简单，计算速度快，且方便修改。因此本例保持规则库和隶属函数不变，以输入和输出的3个比例因子Ke,Kc,Ku为待优化参量，对其进行染色体编码。

Ke值越大，上升速率大，但同时会使超调量和调节时间增大，甚至产生振荡，使系统不能稳定工作；Kc作用与Ke相反，Kc越小上升速率越大，而Kc过小则会引起大的超调量和调节时间；Ku相当于系统中总的放大倍数，一般Ku加大，上升速度较快，但是Ku过大，将产生较大的超调，严重时会影响稳态工作。

然而同时优化3个参量，算法运行速度依然较慢，于是分析3个参量的关系，做进一步简化。在FLC的早期应用中，人们用简化的规则库进行模糊推理[21]，以减少计算机运行时间。从推理中可得出Ke,Kc的关系为:

Ke+Kc=1

(4)

于是待优化参量可以简化为两个参量：Ke和Ku。Kc可由(4)式得出，由此明显提高运算效率。为了验证这种简化方法的实用性，在仿真过程中对两种方式做了对比实验，详见仿真部分。

3.3.2 确定适应度函数 遗传算法在优化搜索中基本不利用外部信息，仅以适应值函数为依据，利用种群中每个个体的适应度值进行搜索。因此适应度函数的选取，直接影响到遗传算法的收敛速度以及能否找到最优解。在控制系统当中，常用的目标函数为时间乘绝对误差积分准则(integrated time and absolute error, ITAE)：

(5)

式中,|e(t)|为系统误差的绝对值。该式可以综合评价控制系统的响应时间、超调量等动态和静态性能。ITAE的值越小，性能就越好[22]。由于遗传操作是根据适应值大小进行的，且适应值非负，而目标函数的优化方向应对应于适值增加的方向，所以对性能指标函数作适当的变换得到适应度函数：

(6)

3.3.3 确定遗传算法运行参量 运行参量包括种群大小M、种群数量Mp、最优个体最少保持代数Gm、变异概率Pm、交叉概率Pc等。其中种群大小、数量和最优个体最少保持代数对结果和计算时间影响最大，太小优化结果不理想，太大则迭代所需时间较多。变异概率和交叉概率决定系统全局和局部搜索能力，较大时重组个体出现的概率大，收敛快；但同时新旧替换过快，使得一些较优的个体可能被过早淘汰。因此有必要引入人工选择精华种群。

在本例中，SGA参量设定为：M=20,Mp=1,Gm=50,Pc=0.75,Pm=0.05。MPGA参量设定为：M=20,Mp=10,Gm=10，Pm取0.7～0.9间随机数，Pc取0.001～0.05间随机数，不同种群取不同概率，防止早熟。

4 仿 真

本文中所用的光电跟踪系统模型为快反镜实验平台实测所得，其被控对象的传递函数Gv为：

(7)

基础的双闭环反馈控制系统结构如图1所示，设计内环速度控制器Cv为：

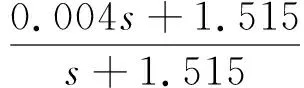
(8)

设计外环位置控制器Cp为：

(9)

以阶跃信号r(t)=500(t)作为测试输入，用示波器显示响应曲线，计算系统JITAE值，以此作为系统阶跃响应综合品质的指标。由于本文中重点研究高型系统对稳态精度的提升，因此截取输出信号的稳态部分计算其平均值，将其与输入信号值作差得到|es|。

为了充分表现经MPGA优化的模糊Ⅱ型控制器的先进之处，分4个步骤进行仿真：(1)在只有位置控制器Cp的系统中实验;(2)在Cp之前并入一个积分环节使系统提升为Ⅱ型，令积分增益k分别为1,5和10做对比实验;(3)在积分环节前接入FLC得到模糊Ⅱ型控制器，如图5所示，令Ke,Kc,Ku都为1，进行实验;(4)引入遗传算法。

为了体现MPGA比SGA的优越，做两组对照试验: (1)GA-1为SGA优化FLC;(2)GA-2为MPGA优化FLC。对以上4个步骤按顺序进行仿真，实验结果在表2中进行总结。

Table 2 Comparison of simulation results

4.1 阶跃响应动态特性分析

为了分别展现FLC和MPGA的对系统动态特性的影响，分两步进行对比。

图9为步骤(1)～步骤(3)的阶跃响应对比图。图中6条曲线分别为：输入信号、步骤(1)输出信号、步骤(2)中3个k值下的输出信号，以及步骤(3)加入FLC后的输出信号。通过对这3个步骤对比，可以得出：接入积分环节之后，超调量随着k值增大而增大，证明系统型别升高会带来震荡，破坏稳定性；而接入FLC之后，与原系统相比，超调量没有变化，说明模糊控制器可以抑制高型震荡。

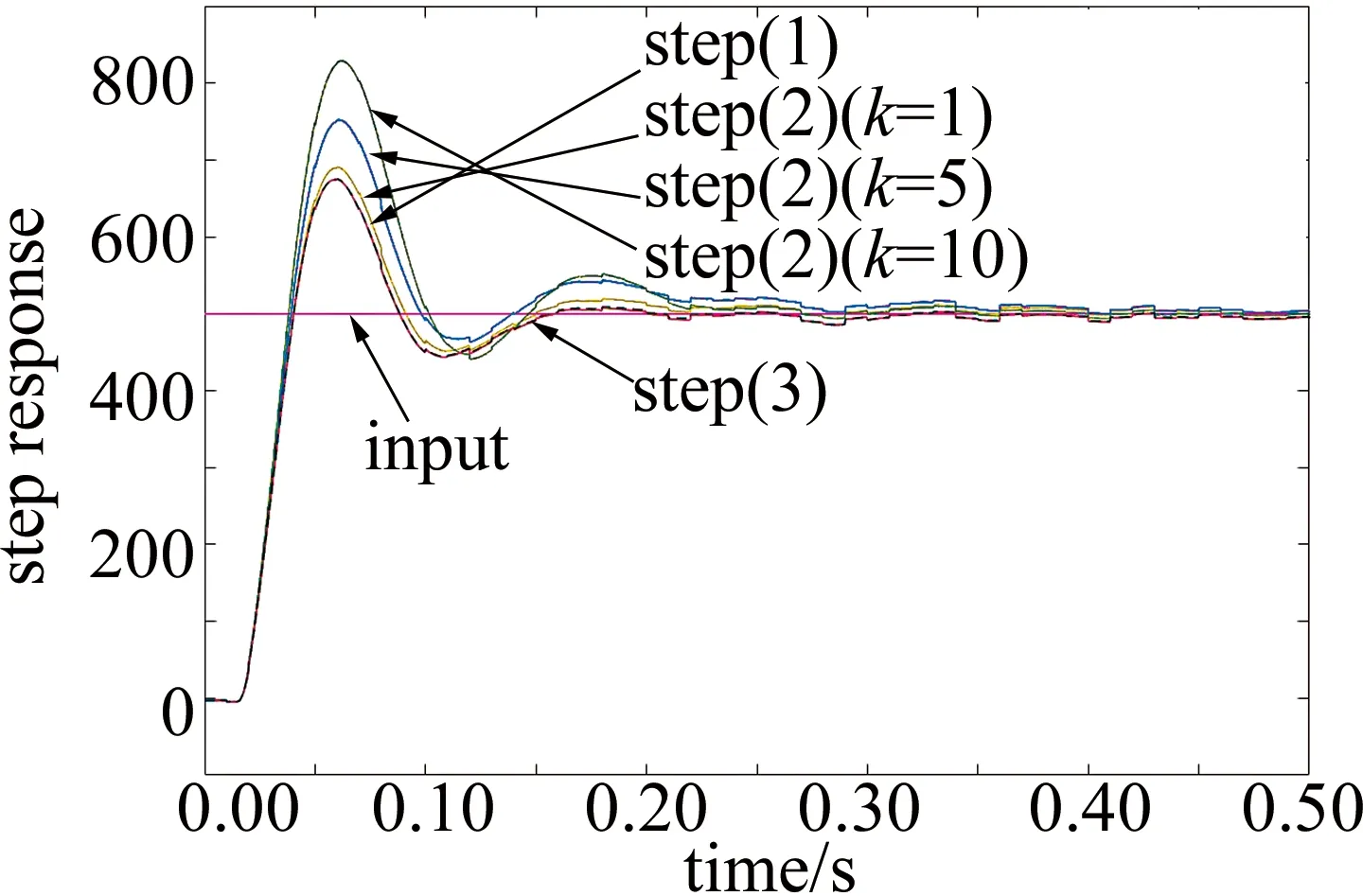
Fig.9 Step response comparison of step (1),(2),(3)

图10为步骤(3)、(4)的阶跃响应对比图，图中5条曲线分别为：输入信号、步骤(1)输出信号、步骤(3)输出信号，以及步骤(4)使用两种遗传算法优化FLC后的输出信号。通过这3个步骤对比，可以得出：经遗传算法优化后的系统阶跃响应无明显变化，说明遗传算法的接入对动态响应特性影响不大。

Fig.10 Step response comparison of step (3),(4)

4.2 阶跃响应稳态特性分析

对图9和图10中0.5s～1s的稳态部分放大，得到图11和图12。再结合表2中各步骤|es|值进行分析。

Fig.11 Enlarged steady-state view of 0.5s～1s in Fig. 9

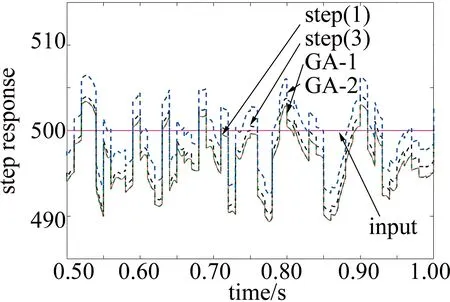
Fig.12 Enlarged steady-state view of 0.5s～1s in Fig.10

由图11可知，对比步骤(1)和步骤(2)可以看出，系统型别升高可以明显减小稳态误差；对比步骤(2)中3个不同k值下的|es|值可知，k值越大，系统稳态误差越小；由步骤(3)可知，FLC的加入会使k值动态变化，稳态误差由k值决定。

由图12可知，经过遗传算法优化之后的系统稳态误差进一步减小,GA-2中稳态误差比步骤(1)减小了88.5%。这符合预期，原因在于遗传算法可以根据系统状态实时调整FLC的3个比例因子，使稳态误差保持最小，不需要依赖专家经验，避免了人为因素的干扰。

4.3 两种遗传算法对比

图13和图14分别为SGA和MPGA的进化过程图。横轴为进化代数，纵轴为适应度函数。SGA虽然在第6代就已经收敛，但是从表2可知，GA-1中Ke≈0，Ku≈0，JITAE与|es|值与步骤(1)无异，FLC实际并没有在系统中起到调节作用，这表明SGA出现早熟收敛问题。而MPGA在第18代收敛到最优值，由表2可知,此时GA-2中JITAE=2.238，|es|=0.41，在所有实验中综合品质最好，稳态精度最高，说明MPGA避免了SGA的早熟收敛问题。

Fig.13 SGA evolution curve

Fig.14 MPGA evolution curve

4.4 动态高型技术的实现

图15为GA-2实验中系统误差与FLC输出关系图。可以看出，随系统误差e与误差变化率Δe的变化，FLC的输出即积分环节的增益也在动态变化。这说明本系统可以动态切换系统型别并且实时调整积分增益，满足了动态高型技术的要求，并证明了动态高型技术在提高系统稳态精度方面的优势。

Fig.15 Relationship between system error and FLC output

综合以上分析可知：经MPGA优化后的模糊Ⅱ型控制器既提高了系统的稳态精度，又抑制型别变化带来的震荡，使系统的综合响应品质达到最好。

5 结 论

在经典Ⅰ型双闭环跟踪控制系统中引入FLC和积分环节，构成了模糊Ⅱ型系统，并用MPGA对FLC的参量进行优化。经过仿真发现，改良后的系统可以根据误差状态判断积分环节的并入与断开，达到了动态改变系统型别的预期目标。并且可以动态改变积分环节增益，消除型别升高带来的动态性能恶化，避免型别切换瞬间带来的抖振问题，同时提高了稳态输出精度和综合响应性能。最终系统的稳态误差比初始系统减小了88.5%，改善效果显著。