格子Boltzmann方法模拟咸水吸收CO2的Rayleigh对流过程

2021-03-08付博田建昌刘菊张润叶陈慕华朱新宝

化工进展 2021年2期

付博，田建昌，刘菊，张润叶，陈慕华，朱新宝

（南京林业大学化学工程学院，江苏南京210037）

化石燃料燃烧导致CO2大量排放引起的温室效应严重威胁着人类赖以生存的地球环境，遏制全球气候变暖、减少大气中CO2浓度成为全球关注的热点。二氧化碳捕集与封存（CO2capture and storage，CCS）是CO2大规模减排应对气候变化的重要手段，被认为是最有潜力和最可行的CO2减排方式[1]。而咸水层在全球分布广泛、碳封存能力强，受到了广泛关注[2]。研究CO2在咸水层的迁移过程，对于设计咸水层封存项目至关重要。在封存阶段，为CO2溶解和迁移提供动力的是分子扩散和界面对流[3-4]。即在气液相界面处CO2通过分子扩散的方式进入咸水，同时界面处已溶解CO2的迁移速率制约着CO2进一步的溶解。与分子扩散相比，界面处的对流传质可明显加快CO2的溶解速率[5]。在CO2溶解过程中，液体密度明显增大，而表面张力减小，因此本文中涉及的对流现象可视为只由密度梯度引发的Rayleigh对流[6]。CO2溶解处密度差持续积累导致重力不稳定，突破黏性阻力发生沉降，而不含CO2的咸水则会向上流动，由此产生对流，加快了CO2进入溶液的速率[7]。在不同地质条件下，除了温度和压力外，咸水层的盐浓度差异也会影响CO2溶解和迁移速率，因此需要了解CO2在溶于咸水过程中对流传质的规律以及盐浓度对传质速率的影响。

目前对于CO2在咸水中的溶解和对流传质过程的研究，主要有实验法和数值模拟法。Khosrokhavar等[8]采用PVT筒检测了CO2溶于盐水过程中密度梯度的变化，整体了解CO2在咸水中的溶解特性。为了更直接地观察和研究自然对流的整个过程，Kneafsey等[9]利用垂直的Hele-Shaw盒子观测了常压下CO2指状Rayleigh对流结构的形成和发展过程，同时指出，外界微小的扰动都会造成不同Rayleigh对流结构的产生。Soroush等[10]也通过Hele-Shaw 盒子实验，验证了Rayleigh对流结构对传质通量的提高具有很强的促进作用。Abad等[11]和Khosrokhavar等[12]的实验结果表明，与在纯水中CO2的溶解过程相比，CO2在咸水中的对流传质过程明显减弱。随着计算机模拟技术的发展，通过建立适当的数学模型来模拟Rayleigh对流的产生和结构变化，可以更清晰直观地了解该过程的机理。MacMinn等[13]和Xu等[14]基于稳定性分析的模拟，研究了CO2注入咸水层后从密度梯度增加到垂直对流发生的过程，并确定了Rayleigh对流开始的临界时间，但未对之后的混合过程进行模拟。Pruess等[15]基于高网格精度数值模拟，研究了CO2的封存过程中溶解-扩散-对流的过程，较好地模拟了Rayleigh对流结构从产生到发展至下边界之前的过程，但该模拟方法只考虑了密度差引起的体积力的影响，对于咸水中盐离子对溶解速率的影响没有进一步探索。

本文在前人研究的基础上，采用格子Boltzmann方法（LBM）模拟研究CO2在溶解于咸水过程中形成的对流结构特点和传质规律以及盐浓度对该过程的影响。与其他数值模拟方法相比，LBM具有数值精度和计算效率高、物理条件清晰、边界条件易处理等优点，可以在介观尺度上有效模拟流体流动和传质过程[16]。本文根据实际的传质过程特点，建立了包含密度分布函数和浓度分布函数的双分布模型，并引入静电力和体积力等外力项。模拟了在气液界面处存在多个饱和CO2扩散源时，Rayleigh 对流从产生到发展再到稳定的全过程，并对CO2在纯水和不同盐浓度溶液中的溶解过程进行了模拟，验证了前人理论分析和实验中所述的盐浓度对Rayleigh对流过程的抑制作用，模拟结果可为CO2捕集与封存提供理论指导。

1 建立Rayleigh对流模拟的LBM模型

1.1 速度场

本文采用Inamuro 等[17]提出的双分布模型，假设双组分流体由溶剂A和溶质B组成，且B的含量远小于A，因此B 对流场变化的贡献可忽略不计。计算过程中采用D2Q9格子模型[18]，见图1。

溶剂A的无外力LBGK演化方程[19]见式(1)。

式中，fAi(x,t)为t时刻在x位置上沿i方向溶剂A的粒子分布函数；τA为A 粒子两次碰撞的时间间隔，即A 粒子分布函数趋于平衡分布函数的松弛时间。

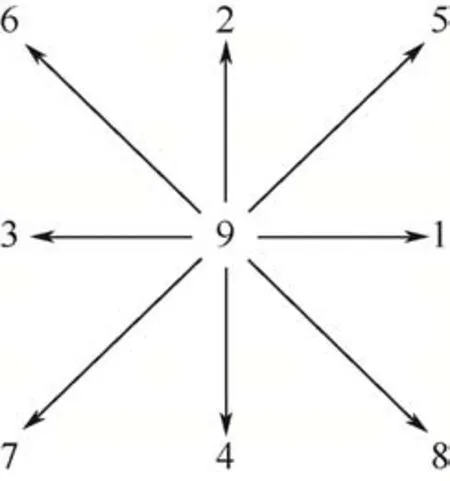
图1 二维九速模型（D2Q9模型）

溶剂A的平衡分布函数见式(2)。

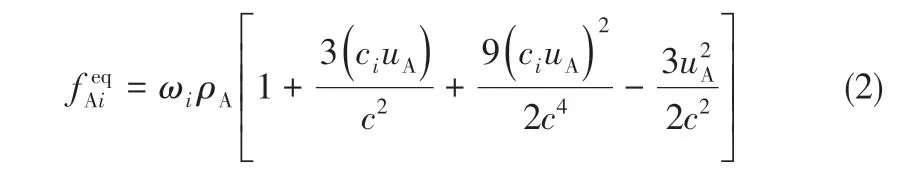
式中，c=Δx/Δt 为格子速度，即单位网格步长和单位时间步长的比值；权重系数ωi和离散速度ci分别见式(3)和式(4)。

可由粒子分布函数计算流场的宏观密度和宏观速度，分别见式(5)和式(6)。

液体黏度见式(7)。

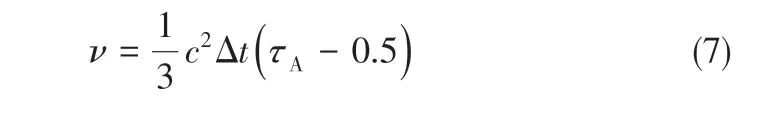
1.2 浓度场

溶质B的粒子分布情况即为该扩散过程的浓度场的变化，无外力LBGK演化方程见式(8)。

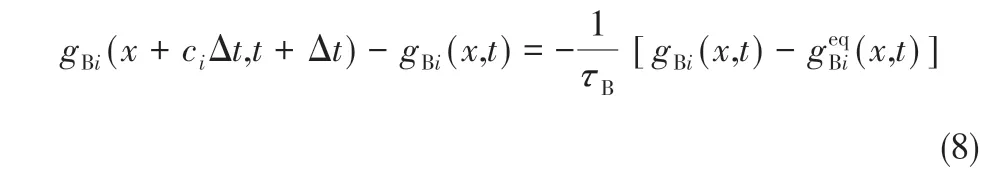
式中，gBi(x,t)表示t 时刻在x 位置上沿i 方向溶质B的粒子分布函数，即浓度分布函数；τB是溶质B的松弛时间。

溶质B的平衡分布函数见式(9)。

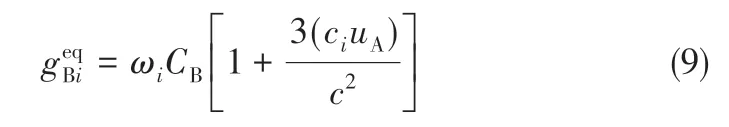
宏观浓度见式(10)。

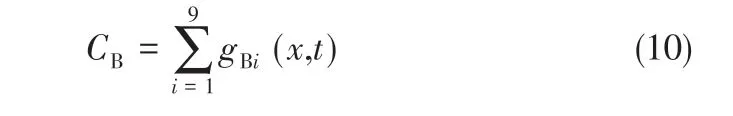
溶质扩散系数[20]见式(11)。

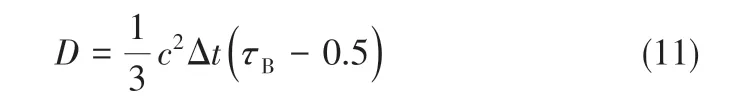
1.3 双分布模型

本文采用Buick 等[21]提出的混合模型，通过修改碰撞项和平衡分布函数，将速度场和浓度场耦合，达到处理外力的目的。

在该体系中，盐、水和二氧化碳之间存在3种相互作用力：①离子和水分子间的静电力；②二氧化碳和水分子之间的范德华力；③离子和二氧化碳分子间的静电力。Chalbaud 等[22]和Aggelopoulos等[23-24]研究表明，在该体系中，离子与二氧化碳之间的作用力占主导，其他两种力远小于该力。流场中钠离子、氯离子与CO2分子间的静电力作用产生的势能[25]分别见式(12)和式(13)。

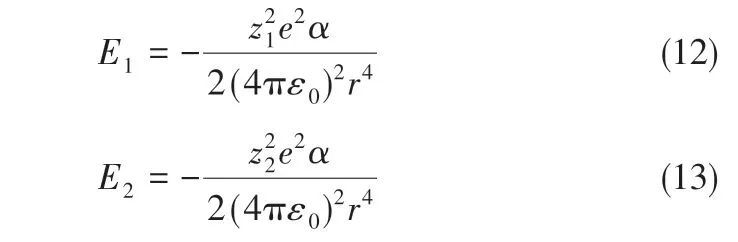
式中，z1和z2分别为钠离子和氯离子的带电荷数；e为单位电荷的带电量，取1.602177×10-19C；α为二氧化碳的极化率；ε0为真空介电常数；r 为离子与分子中心之间的距离，为计算方便，距离统一取临界间距0.5nm[26-27]。

除了盐的静电力外，咸水吸收CO2会引起体系密度的变化，由此产生的体积力也是Rayleigh对流传质过程中的重要驱动力之一[28]。本文采用Boussinesq 近似[29]来处理体积力，即假设流体密度是浓度的线性函数，由此产生的体积力见式(14)。

因此，单位体积的溶质粒子在格子结点上受到的总作用力势能见式(15)。

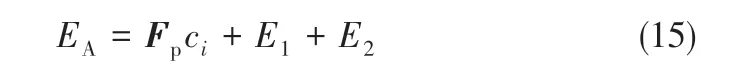
修改后的碰撞方程见式(16)。

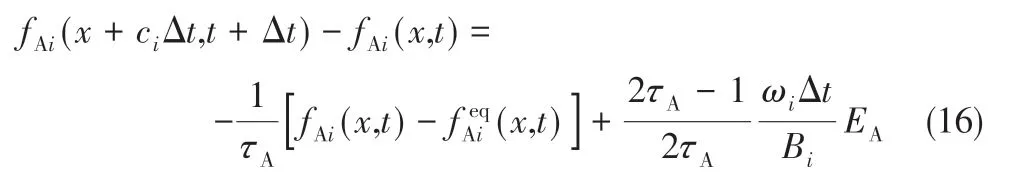
式中，Bi为速度系数，其目的是加入受力影响时，保证质量和动量守恒。其中B1=B2=B3=B4=B9=6，B5=B6=B7=B8=24。

修正后平衡状态函数中的速度见式(17)。

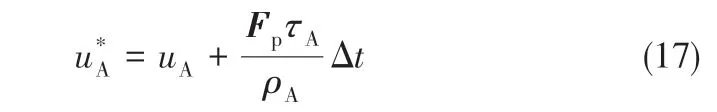
外力修正后的流场速度[30]见式(18)。

修正后的平衡状态方程分别见式(19)和式(20)。

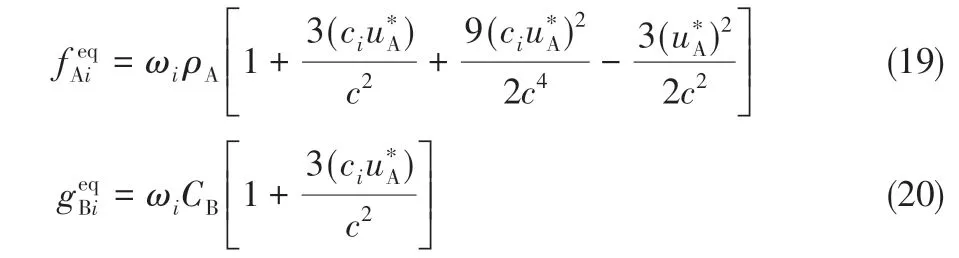
1.4 边界处理

计算区域如图2 所示，区域的高为H，宽为L，温度和压力设置为293.15K、101kPa，并忽略传质过程中温度的变化。初始时刻，液相为静止的、均匀的NaCl 水溶液，各结点速度和CO2浓度均为0。区域下边界为静止无滑移壁面，采用标准反弹边界[31]；为防止左右两侧对Rayleigh 对流结构的发展产生影响，左右采用周期边界[19]；上边界是无变形气液自由界面，采用镜面对称边界[32]；扩散源处CO2的浓度为饱和浓度，采用恒浓度边界处理[33]。此时，CO2及其饱和溶液的物性见表1。

图2 Rayleigh对流计算区域

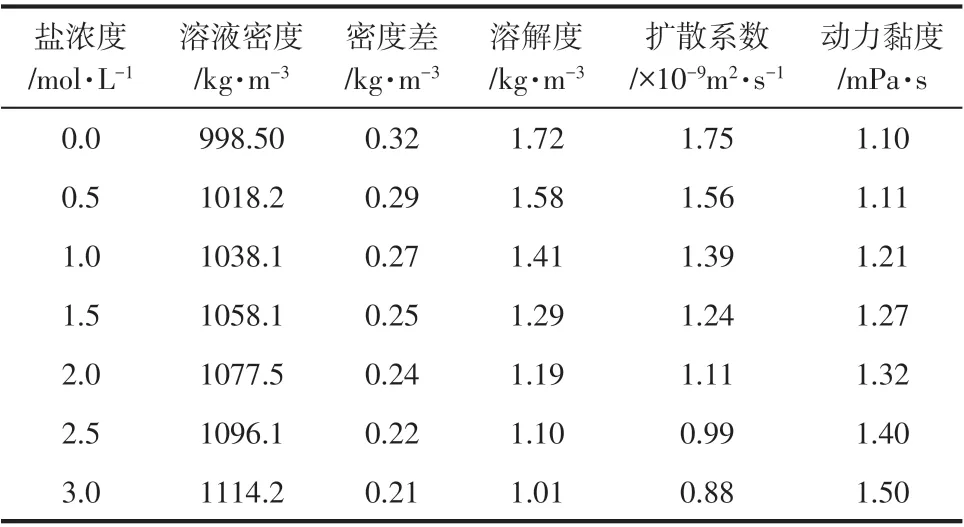
表1 不同NaCl浓度咸水饱和二氧化碳溶液物性[34-37]

2 Rayleigh对流的LBM模拟和分析

本文采用Matlab 软件编程，计算过程主要包括粒子碰撞和迁移[38]：①初始化流场每个结点的变量及分布函数；②计算每个结点的宏观物理量，代入式(19)和式(20)，由此得到粒子的平衡分布函数；③在每个结点上进行碰撞计算；④在流场内部结点中，将粒子迁移到相邻结点；⑤在边界结点上进行边界条件处理；⑥得到经过一次碰撞和迁移后的宏观量，并作为下一次迭代的初始值，经过多次迭代计算，最终得到传质过程中的速度场和浓度场。

2.1 单个及多个溶质扩散源的模拟

2.1.1 单个溶质扩散源的模拟

对于单个CO2扩散源的传质过程，设定的计算区域高H=5mm、宽L=5mm，网格划分为100×100，则单位网格长度为Δx=0.05mm。图3 给出了单个CO2扩散源溶解于1.0mol/L 的NaCl 溶液过程中，溶质浓度分布情况的模拟结果及相关实验图像。

由图3 的浓度变化可知，在只有单个CO2扩散源时，指状对流结构不受墙壁和其他对流结构的影响，界面处CO2浓度较高的液体沿重力方向流动，逐渐发展为对称的Rayleigh 对流结构，头部圆润，尾部瘦小，具有明显的流线型轮廓，这与图3(c)中Thomas等[39]实验观察到的对流结构十分相近。

2.1.2 多个溶质扩散源的模拟

对于多个扩散源的传质过程，设定的计算区域高H=10mm、宽L=20mm，网格划分为100×200，则单位网格长度Δx=0.1mm。n个CO2扩散源均匀分布在气液界面，图4 给出了n=5 时CO2溶解于1.0mol/L的NaCl溶液过程中不同时刻溶质的浓度分布情况。

由图4的浓度分布可知，指状对流结构经历了从生长到发展再到触底反弹的过程。t=50s左右时，在气液界面处形成了5个指状对流结构，并且开始相互诱导。t=100s时，两侧的指状对流结构（扩散源1和2，4和5）从根部合并，完全融合并形成较大对流结构，继续向下和两侧发展。t=150s时，原来的5个指状对流结构在根部合并，对流结构末端向上折返，为大对流结构向下发展提供条件，这种分支和逆向流动可促进传质，与沙勇等[40]通过双光路纹影仪实验观察到的半圆形小涡流结构非常相似。下半部分的两个分支到达下边界后，在壁面的影响下向上返回，并继续在横向发展。t=200s 时，原先两个分支向下发展融合成一体，Rayleigh 对流结构发展充分，达到稳定状态。

2.1.3 壁面阻力的影响

本文模拟计算的对象是类似于Hele-Shaw盒子实验的设定区域，两块垂直的薄板间隙非常小，因此可以将实际三维的薄板间的Rayleigh对流过程近似为二维层流流动，服从平面泊肃叶流规律，受到的壁面阻力可表示为式(21)[41]。

式中，δ 为壁面位置；μ 为溶液的动力黏度。将式(21)代入式(17)和式(18)，分别修正平衡速度和流场速度，由此实现壁面阻力对该过程的影响。模拟结果如图5 所示，扩散源数n=5，比较在t=150s时不同壁面位置处x-y截面的浓度分布图可知，随着与壁面的靠近，壁面阻力带来的影响越来越大，Rayleigh对流过程受到抑制。

2.2 盐浓度对Rayleigh对流结构的影响

在293.15K、101kPa 下，分别在纯水和摩尔浓度为0.5mol/L、 1.0mol/L、 1.5mol/L、 2.0mol/L、2.5mol/L 和3.0mol/L 的溶液中进行了二氧化碳在溶液中的自然对流传质模拟。设定的计算区域高H=10mm、宽L=20mm，网格划分为100×200，单位网格长度Δx=0.1mm。图6 给出了n=7 时不同盐浓度和不同时刻溶质的浓度分布情况。

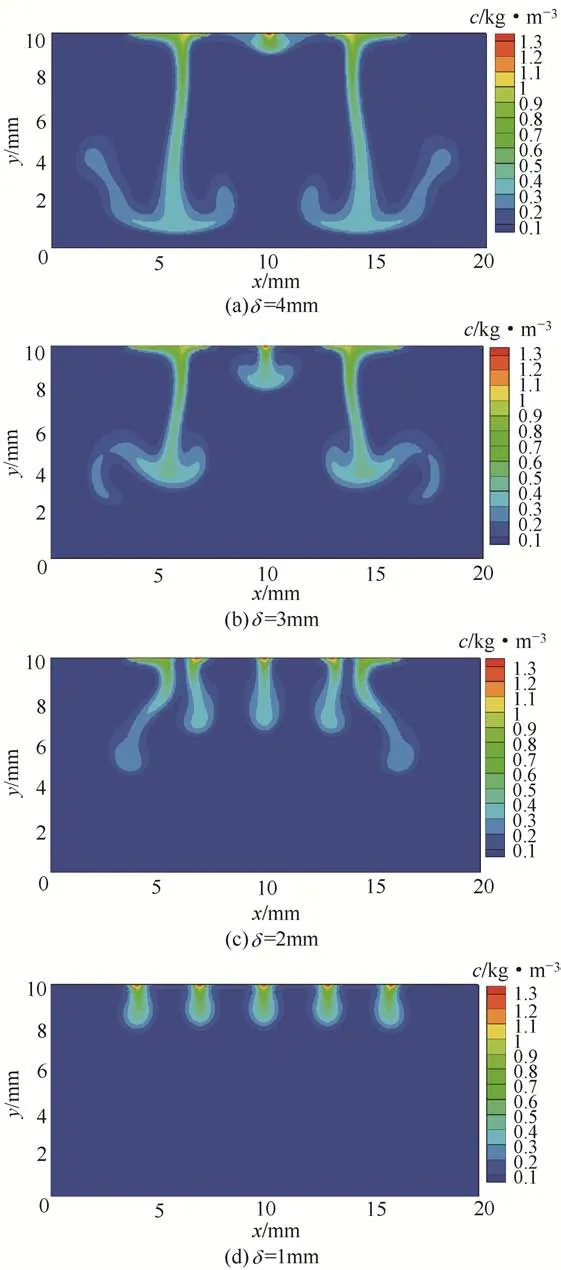
图5 n=5、t=150s时不同壁面位置处x-y截面的浓度分布

观察图6 中的浓度变化可知，在t=50s 时，纯水以及盐浓度c0≤1.0mol/L 的溶液中，气液界面附近出现了明显的指状对流结构，并且结构之间相互诱导，开始发生形变；而在盐浓度c0＞1.0mol/L的溶液中，指状对流结构发展缓慢，结构之间几乎没有影响。在t=100s 时，纯水以及盐浓度c0=0.5mol/L 的溶液中，小指状对流结构在根部合并，合并后大指状对流结构迅速向下发展并往横向延伸，未参与合并的指状对流结构发展缓慢；在盐浓度c0＞0.5mol/L 的溶液中，小指状对流结构还未发生融合。在t=200s 时，所有溶液中的对流结构在近气液界面处完全融合，向下发展的大指状对流结构触底反弹。其中，纯水以及盐浓度c0≤1.0mol/L 的溶液中，大指状对流结构已发展至底部并趋于融合，致使底部平均浓度较高，以向上发展为主；而在盐浓度c0＞1.0mol/L 的溶液中，部分指状对流结构还未发展至溶液底部。

图6 的模拟结果表明，随着溶液盐浓度的增大，指状对流结构出现的时间会推迟，并使后续的对流传质过程减弱。这与杨盼瑞等[42]通过实验观测到的二氧化碳在咸水中盐浓度对扩散系数的影响情况一致。由此可知，对于不同盐浓度的地质条件，CO2封存过程必须充分考虑盐浓度对CO2扩散和对流传质的影响。

2.3 模拟结果分析

2.3.1 对流发生时间及流场速度分析

在1.0mol/L 的NaCl 溶液中，不同扩散源个数时对流的开始时间模拟结果如图7 所示。由图可知，随着扩散源个数的增加，Rayleigh 对流发生的时间越来越长。至n=40 时，对流发生时间tonset=52.4s，与Loodts等[43]对连续扩散源模型的对流发生时间理论预测值55.95s±0.07s较接近。

在1.0mol/L的NaCl溶液中，扩散源个数n分别为10、20、30 和40 时，模拟流场的平均速度随时间的变化关系如图8所示。模拟流场的平均速度随时间的变化先增大后减小，即相较于前期扩散对流场速度的影响，Rayleigh 对流可有效加快流场速度；随着对流结构趋于稳定，流场速度也开始下降。同时比较不同扩散源个数的平均速度变化趋势可知，随着扩散源个数的增加，速度的变化也会延迟。比较模拟得到的流场平均速度值与Thomas等[39]实验中测得的流场速度1.82×10-4m/s 可知，模拟结果与实验值具有相同的数量级。

2.3.2 盐浓度对传质通量的影响

瞬时传质通量即单位时间通过单位截面积所传递物质的质量。由模拟结果得到的不同时刻CO2在流场中的浓度分布情况，可进一步计算传质过程中不同时刻的瞬时传质通量Nins,t[kg/(m2·s)]，见式(22)。

图9 给出了界面扩散源数n=7 时CO2在纯水和c0=1.0mol/L、2.0mol/L、3.0mol/L的咸水中瞬时传质通量Nins,t随时间的变化关系。

观察图9 可知，对于不同盐浓度的溶液，Nins,t随时间增长的变化趋势是一致的，都经历了先减小后增大再减小的变化。即前期气液界面的传质以分子扩散为主，由Fick定律可知，随着CO2的不断溶解，界面处的浓度梯度减小，传质速率变慢；而后随着界面处与液相主体的密度差不断增大，界面失稳，高密度液体克服黏性力向下流动，并将液相主体的溶液挤压到上方，促进了液体表面更新，Rayleigh 对流结构不断向下和向两侧发展并相互诱导融合，使得对流结构在溶液中快速扩展，Nins,t也因此增大；最后，下边界阻碍了Rayleigh对流结构的发展，同时主体流场的浓度梯度差已经较小，抑制了CO2在溶液中的扩散，Nins,t开始减小。

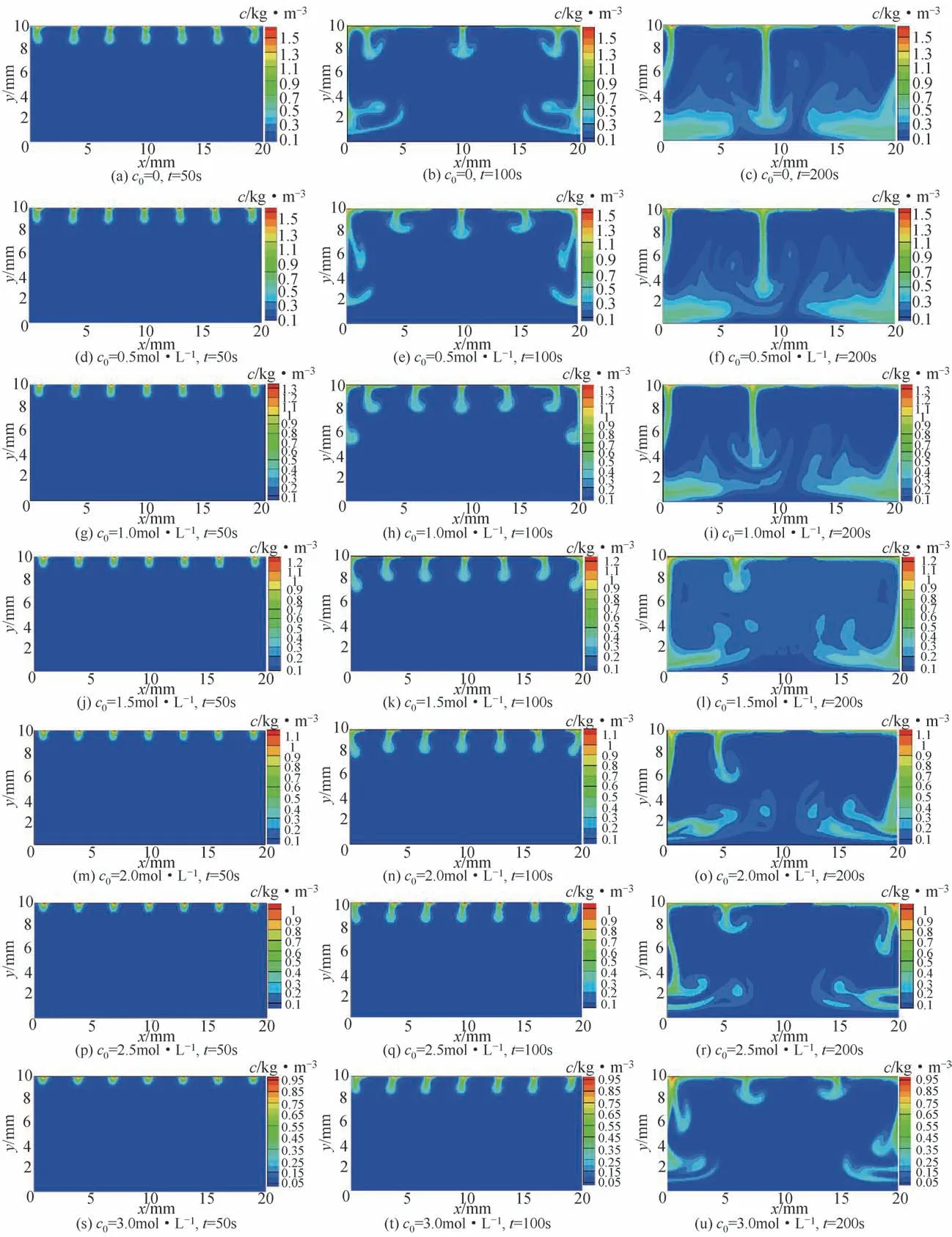
图6 n=7时不同盐浓度和不同时刻溶质的浓度分布

图7 扩散源个数n=1～40时Rayleigh对流开始时间的变化

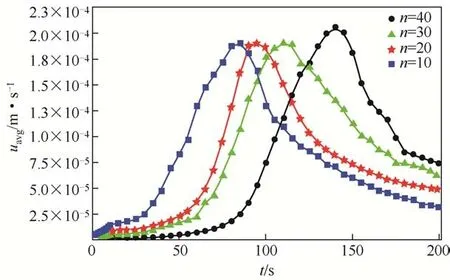
图8 n=10、20、30、40时流场平均速度随时间变化关系

图9 n=7时CO2在纯水和不同盐浓度咸水中瞬时传质通量Nins，t随时间变化关系

将模拟结果与George 等[44]计算结果对比可知，两者的瞬时传质通量的数量级［mg/(m2·s)］相同。同时，观察图9 中各个盐浓度下Nins,t的最高点出现时间可知，纯水和c0=1.0mol/L、2.0mol/L、3.0mol/L咸水中的出现时间分别为t=100s、125s、155s、200s左右，即盐浓度的增加造成了Rayleigh对流发展的滞后，这与图6中结果以及前人实验得到的结论相吻合。同时观察不同盐浓度下Nins,t的变化曲线可知，盐浓度的增加会降低CO2的瞬时传质通量。由此可知，盐浓度的增加会抑制Rayleigh对流的发生和发展，使气液传质速率总体降低。