一种面向动态异构信息网络的高效极大motif团挖掘方法
2021-03-08周军锋
丁 晨,周军锋,杜 明
(东华大学,上海 201620)
0 引言
当前社会处于信息时代,数据类型繁杂多样,异构信息网络[1-2]是一种把顶点与类型标签相连的数据图,用于刻画不同类型对象间的复杂限制语义。相比于顶点类型单一的数据图,异构信息网络可以用不同类型的实体及实体间联系表达出多元化、交互性高的信息。
异构信息网络常与motif[3-5]结合,motif用于给定不同类型顶点间的限制关系,通过发现极大motif团[6]可以在异构信息网络上挖掘有价值的信息。常见的异构信息网络,如生物网络、书目数据库和共同购物图等,已被应用于各种领域[7-9]。如图1所示,在异构信息网络G中,顶点类型分为三类:作者类型、论文类型、会议类型,给定motif M所示的顶点关系,通过挖掘极大motif团,可以找到有合作关系的作者。
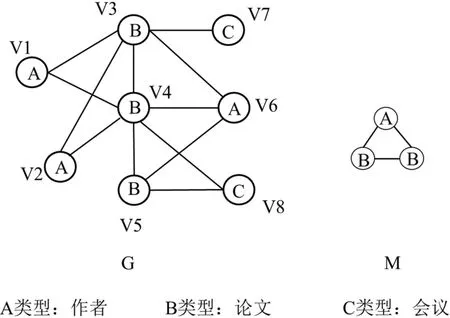
图1 异构信息网络Fig.1 heterogeneous information network
异构信息网络和极大 motif团有很高的实用价值。然而,异构信息网络不是一成不变的,它在实际应用中会频繁更新,由此衍生出如何实时更新极大motif团的问题。现有算法META(the maximal m-clique enumeration algorithm)可以在静态图上快速发现极大 motif团,但不支持在动态图上更新极大 motif团。为了实现更新操作,该算法需要在图变化后重新枚举极大 motif团,这种做法存在大量冗余,效率不高。
针对现有算法的不足,本文提出一种支持极大motif团更新的高效算法UMMD(the algorithm of updating maximal motif-clique on dynamic HINs)。该算法主要由加边策略、减边策略构成。其基本思想是:在加减边时,只处理与边两端顶点关联的极大 motif团,从而缩小更新范围,避免枚举操作。实验结果表明,本文提出的算法可以高效地在动态异构信息网络上挖掘极大motif团。
1 背景知识和相关工作
1.1 相关概念和问题定义
定义 1 异构信息网络:异构信息网络是一个四元组G=(V, E, T, F),V代表图G中顶点的非空有限集合,E代表图G中边的有限集合,T代表图G中顶点类型的非空有限集合,F是一个类型函数,用于对图中每个顶点分配一个T中的顶点类型,每个顶点的类型在给定后不改变。本文的异构信息网络均是无向图。
如图1所示,G是一个异构信息网络,其包含三种类型的顶点。
定义2 motif:对于异构信息网络G=(V, E, T,F),motif是一个四元组M=(Vm, Em, Tm, Fm),Vm代表M中顶点的非空有限集合,|Vm|不大于|V|;Tm代表M中顶点类型的非空有限集合,Tm⊆T;Fm是一个类型函数,用于对M中每个顶点分配一个Tm中的类型;Em代表M中边的有限集合,对于∀(um, vm)⊆Em,F(um)类型的顶点与F(vm)类型的顶点在G中允许相连。
定义3 motif匹配点集:给定异构信息网络G=(V, E, T, F)、motif M=(Vm, Em, Tm, Fm),对于一个非空点集H⊆V,如果|H|=|Vm|,且H与Vm存在一种双射关系f,即对∀u∈H,F(u)=Fm(f(u)),那么H是motif匹配点集。
例如,对于图1的G,点集{1,3,4}、点集{1,4,5}均是motif匹配点集,点集{4,5,8}则不是motif匹配点集。
定义4 motif导出子图:给定异构信息网络G=(V, E, T, F)、motif M=(Vm, Em, Tm, Fm),G′=(V′,E′, T′, F′)是 G 的一个导出子图,如果|V′|=|Vm|,且V′与Vm存在一种双射关系f,即对于∀u∈V′,F(u)=Fm(f(u))且∀u, v∈V′,(u, v) ∈E′,(f(u),f(v))∈Em,那么G′是一个motif导出子图。
例如,在图1的G中可以找到4个motif导出子图,它们对应的点集分别是{1,3,4}、{2,3,4}、{3,4,6}、{4,5,6}。
定义5 motif团:给定异构信息网络G=(V, E,T, F)、motif M=(Vm, Em, Tm, Fm),G′=(V′, E′, T′, F′)是G的一个导出子图,如果|T′|=|Tm|,G′中至少有一个motif匹配点集,且G′的每个motif匹配点集都是motif导出子图,G′是一个motif团。
例如,对于图1的G,点集{1,2,3,4}构成的子图是motif团,但点集{3,4,5,6}、点集{4,6,8}构成的子图均不是motif团。
定义6 候选顶点:对于一个motif导出子图,如果一个顶点能与它组成 motif团,则称该顶点为此motif导出子图的候选顶点。
定义7 极大motif团:如果一个motif团不被图中的其他 motif团包含,那么它是一个极大motif团。
例如,对于图1的G,点集{1,2,3,4,6}、点集{4,5,6}构成的子图均是极大motif团。G中作者类型顶点与论文类型顶点的边,代表某作者撰写了某论文;论文类型顶点间的边,代表两篇论文的研究方向相似。给定 M 所示的顶点关系,一个motif导出子图代表一个作者撰写了两篇研究方向相似的论文,一个极大 motif团可以代表有合作关系的作者们共同撰写了数篇方向相似的论文。当找到G中所有的极大motif团时,也就找到了全部合作过的作者以及他们撰写的论文。
问题定义给定动态异构信息网络G=(V, E,T, F)、motif M=(Vm, Em, Tm, Fm)、已有的极大 motif团,在G发生变化后更新极大motif团。
文中符号的含义如表1所示。

表1 符号解释Tab.1 symbol interpretation
1.2 相关工作
motif是大型信息网络的基本构建模块,常被应用于神经科学、生物学、社会网络等领域。Gurukar[10]等人研究了动态交互网络中通信 motif的挖掘,并开发了COMMIT技术。COMMIT技术将动态网络转换为序列数据库,从而更快地在网络中发现motif。Benson A R[11]通过使用motif解决了 motif-aware的图聚类问题,Stefani L[12]解决了计算motif频率的问题。
胡佳峰等人首次提出了文献[6]中的极大motif团发现算法META,该算法的输入是异构信息网络G、motif M,输出是图中所有的极大motif团。如图1所示,META可以根据给定的G和M,快速枚举出 G中所有的极大 motif团,即mmc{1,2,3,4,6}、mmc{4,5,6}。
META算法的基本思想如下:根据现有的子图匹配算法 VF3[13],找到图中所有的 motif导出子图,对每一个motif导出子图,仿照BK算法[14],通过维护三个不同功能的点集 U、C、NOT来枚举求解它的极大motif团。点集U用来存放当前正在被枚举的 motif团,U里的点可以构成一个motif团,但不一定是一个极大motif团,U的初始状态是空集;点集C是候选顶点集,C里的每个顶点都可以加入U中的motif团,C的初始状态是所有顶点的集合;点集NOT是禁止集,NOT里的每个顶点也都可以加入U中的motif团,但如果一个顶点被存放在NOT里,意味着包含该点的所有极大motif团已经被枚举过,NOT的初始状态是空集。在枚举过程中,当点集C与点集NOT都为空时,U里存放的便是一个极大motif团。
2 支持极大 motif团更新的高效算法UMMD
对于动态异构信息网络的变化,本文研究图加边、减边两种情况。加边指的是每次在图中添加一条不存在的边;减边指的是每次从图中删去一条存在的边。现有算法在图发生变化后会重新枚举,其更新范围是全图,且枚举过程存在冗余。针对上述问题,本文提出以下更新策略。
2.1 加边策略
本文的加边策略通过选择性更新来剪枝更新范围,即只更新与新边两端顶点相连的原有极大motif团,并通过枚举候选顶点补充更新结果。
根据定义,极大motif团可看作由motif导出子图构成。如图1所示,G中的 mmc{1,2,3,4,6}是由 me{1,3,4}、me{2,3,4}和 me{3,4,6}构成。易知,图中出现了新的 motif导出子图后,才会出现新极大motif团。用(u, v)表示边,在动态异构信息网络上加边后,当图中先出现包含点u和点v的新motif导出子图后,才会出现新极大motif团,这说明新极大motif团一定是包含点u和点v的。因此,与点u和点v均不相连的原有极大motif团不会变化,只需选择性更新包含点u或点v的原有极大 motif团。具体来说,对于包含点 u的极大 motif团,判断点 v能否加入其中;对于包含点v的极大motif团,判断点u能否加入其中。
上述方法虽然缩小了更新范围,但可能会出现更新过程中丢失极大 motif团的问题。如图 2所示,G中的原有极大motif团是mmc{1,3,4,5}、mmc{2,4,6},在G上插入边(2,5)后,选择性更新原有极大 motif团,即 mmc{1,3,4,5}、mmc{2,4,6},判断点2不能加入mmc{1,3,4,5},因此mmc{1,3,4,5}不发生变化;判断点5可以加入mmc{2,4,6},从而将mmc{2,4,6}变为mmc{2,4,5,6}。更新过程结束,但新极大 motif团 mmc{1,2,4,5}未发现。造成这种情况的原因是新边的顶点可能与原有极大motif团的子集结合,从而形成新极大motif团。
通过枚举未发现的新 motif导出子图的候选顶点可以解决上述问题。例如,图2的G加入边(2,5)后,图中出现新motif导出子图me{2,4,5}、me{2,5,6},它们的候选顶点是点1、点4、点6。而新极大motif团mmc{2,4,5,6}包含了点4、点6,不包含点 1,说明还有包含点 1的新极大 motif团未发现。通过现有的枚举算法可以找出mmc{1,2,4,5},从而完善更新结果。
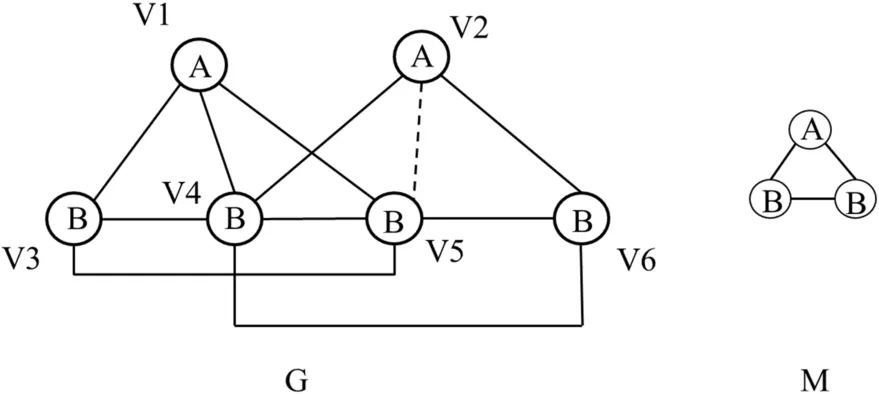
图2 候选顶点示例Fig.2 examples of candidate vertices
算法 1详细介绍了加边策略的过程。将新motif导出子图的候选顶点存进cands(第1行)。如果cands为空,说明新motif导出子图没有候选顶点,它本身便是一个极大motif团(第2-4行)。选择性更新极大motif团,并维护cands(第5-13行)。如果cands不为空,进行枚举操作补充更新结果(第14-15行)。本文在判断一个点能否加入motif团、枚举候选顶点时使用了文献[6]的方法。


下面以图3为例介绍UMMD-insert的算法过程。给定动态异构信息网络G、motif M,假设在G上插入边(3,5),原有极大motif团是mmc{1,2,3,4,6}、mmc{4,5,6}。图中新出现的motif导出子图是me{3,5,6},它的候选顶点是点4,将其存进cands。更新 mmc{1,2,3,4,6},判断点 5能否加入其中,点 5不可以加入,mmc{1,2,3,4,6}不变化;更新mmc{4,5,6},判断点3能否加入其中,点3可以加入,将mmc{4,5,6}变为mmc{3,4,5,6},并将点4从 cands中删去。因为 cands为空,直接输出mmcs作为更新后的极大motif团。
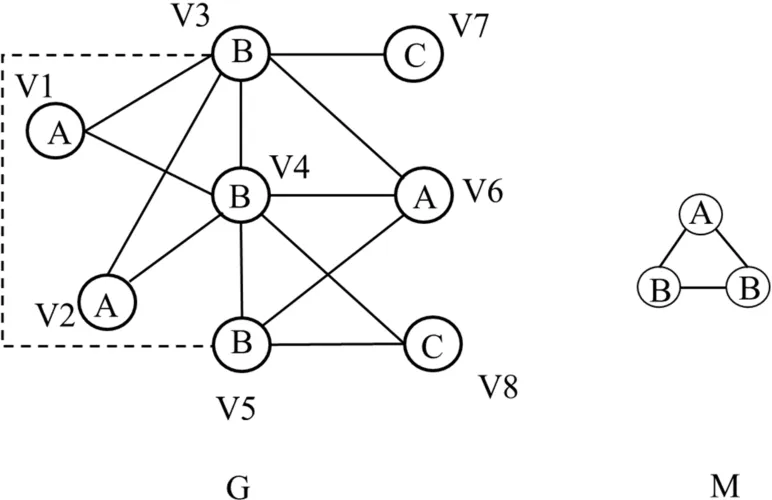
图3 图更新示例Fig.3 examples of graph updating
2.2 减边策略
本文减边策略也通过选择性更新剪枝更新范围。在动态异构信息网络上减边后,只处理同时包含边两端顶点的原有极大 motif团,对其进行更新操作。
用(u, v)表示边,在动态异构信息网络上减边后,对一个原有极大motif团mmc的更新操作可以具化为删除其中的点u或点v。对于一个顶点,如果mmc中不存在包含该点的motif导出子图,说明它无法与mmc中的其他点构成motif团,需将其从mmc中删除,反之,将该点保留在mmc中。
例如,假设在图 1中删除边(2,4),选择性更新原有 mmc{1,2,3,4,6}。me{2,3,4}不再成立,点2在mmc中没有其他关联的motif导出子图,故将点2从mmc{1,2,3,4,6}中删去;点4在mmc中与me{1,3,4}、{3,4,6}有关联,故保留在mmc{1,3,4,6}中。mmc{1,3,4,6}是一个图更新后的极大motif团。但是,对于一个极大motif团,经历上述操作后,也可能被删减为其他原极大 motif团的子集。因此,在更新结束后,需要把更新结果与其他原极大 motif团比较,去除结果中的伪极大motif团。
算法2详细介绍了减边策略的过程。用(u, v)表示边,在动态异构信息网络上减边后,设置set存储更新结果,使其初始值为空集,找出同时包含点u和点v的极大motif团mmc,对其进行更新操作(第1-3行)。选择性更新极大motif团(第2-8行)。当set不为空时,通过与原有极大motif团比较,判断它们中是否存在伪极大motif团(第9-13行)。

下面以图3为例介绍UMMD-delete的算法过程。给定异构信息网络G、motif M,假设从G中删去边(3,5),原有的极大 motif团是 mmc{1,2,3,4,6}、mmc{3,4,5,6}。在G上删除边(3,5)后,更新mmc{3,4,5,6}。因为 me{3,4,6}、me{4,5,6}是mmc{3,4,5,6}的子集,将mc{4,5,6}、mc{3,4,6}存进set,并把mmc{3,4,5,6}从mmcs中删除。再通过比较发现 mc{3,4,6}是原有极大 motif团mmc{1,2,3,4,6}的子集,即 mc{3,4,6}是一个伪极大motif团,而mc{4,5,6}不是任何原有极大motif团的子集,mc{4,5,6}可作为一个新极大motif团,更新结束。
2.3 算法分析
给定动态异构信息网络G、motif M,在G上插入边后,UMMD算法的平均算法时间复杂度为O(|Nmmc|·|Vmmc|·|V/E|);在 G 上删除边后,UMMD算法时间复杂度为 O(|Nmmc|·|Nme|·lg|Vmmc|)。|Nmmc|代表 G中包含点边两端顶点的极大 motif团的个数,|Vmmc|代表 G中极大 motif团的平均点数,|Nme|代表G中motif导出子图的个数,|V/E|代表 G中顶点的平均度数,其中|V|代表 G的点数,|E|代表G的边数。
使用基础算法META枚举极大motif团的最坏时间复杂度是O(n!·n2),最好时间复杂度也要大于 O(n2),其中n为图的顶点数。因此,UMMD算法的更新效率更高。
3 实验
3.1 实验环境
实验所使用的硬件配置是Inter Core i7主频为2.60GHz的CPU,16GB的RAM内存,Windows 10 64位系统;实验的运行环境为Microsoft Visual Studio 2017,解决方案是Release,解决方案平台是x64。
实验用于比较的算法:(1)META算法;(2)UMMD算法。以上算法均采用C++语言实现。
3.2 数据集
本文使用12个实验数据集进行实验,数据集基于4个真实异构信息网络,分别是Reactome、Amazon、Yeast、Instacart。异构信息网络与motif相结合,motif的顶点规模会影响算法挖掘极大motif团的效率,所以本文将一个异构信息网络与点数3、点数5、点数7的motif相关联,生成12个数据集。例如,用 Reactome-3、Reactome-5、Reactome-7表示Reactome不变,将其分别与点数为3、5、7的motif相关联。
数据集Reactome是一个生物信息网络,主要描述了蛋白质大分子、生物行为作用、不同物种间的交互信息;数据集 Amazon来自于亚马逊网站,图中共有4种不同类型的顶点,商品类型顶点之间的边代表两个商品是在同一次购物过程中购买的。数据集 Yeast是一个蛋白质分子生物网络,共有71种顶点类型;数据集Instacart是一个购物网站的异构信息网络,顶点类型有21种,商品类型顶点之间的边代表两个商品被同时购买超过 200次。4个基本异构信息网络的相关统计信息如表2所示,其中|V|和|E|分别表示图中的顶点数以及边数。

表2 数据集统计信息Tab.2 statistics for the dataset
3.3 性能分析与比较
本文为了直观显示更新效率,以更新极大motif团的时间开销作为算法性能指标。此外,本文实验还研究图变化次数对算法性能的影响。本章将以不同的加减边数目进行实验,对于加边,本文随机在图中插入 100/1 000条原本不存在的边;对于减边,随机在图中删除100/1 000条已存在的边。用于对比的算法有META算法、UMMD算法。规定时间单位为秒,UMMD算法的更新时间精确到小数点后一位,Inf表示算法在 30 000秒内没有输出更新结果。
各算法在图增加 100条边的更新时间如表3所示。观察发现,在增加100条边时,UMMD算法的更新效率比META算法快约2个数量级。在较大数据集Amazon-3、Amazon-5上,UMMD算法比 META算法分别快 234倍、238倍,在Reactome-3数据集上,UMMD算法比META算法快768倍,在Yeast-3、Instacart-3等较小数据集上,UMMD算法约快300倍。

表3 插入100条边的更新时间Tab.3 the update time of inserting 100 edges
以上说明,UMMD算法的更新效率均比META算法更高。这主要是因为本文的更新策略可以缩小更新范围,只处理与边两端顶点相连的极大motif团,而META算法是对全图进行重新枚举,存在冗余。
各算法在图上删除100条边的更新时间如表4所示。在大部分数据集上,UMMD算法的效率比META算法快2个数量级。在Yeast-3数据集上UMMD算法快327倍,在Instacart-5数据集上快249倍,在Amazon-5数据集上快781倍,在Reactome-5数据集上快54倍。
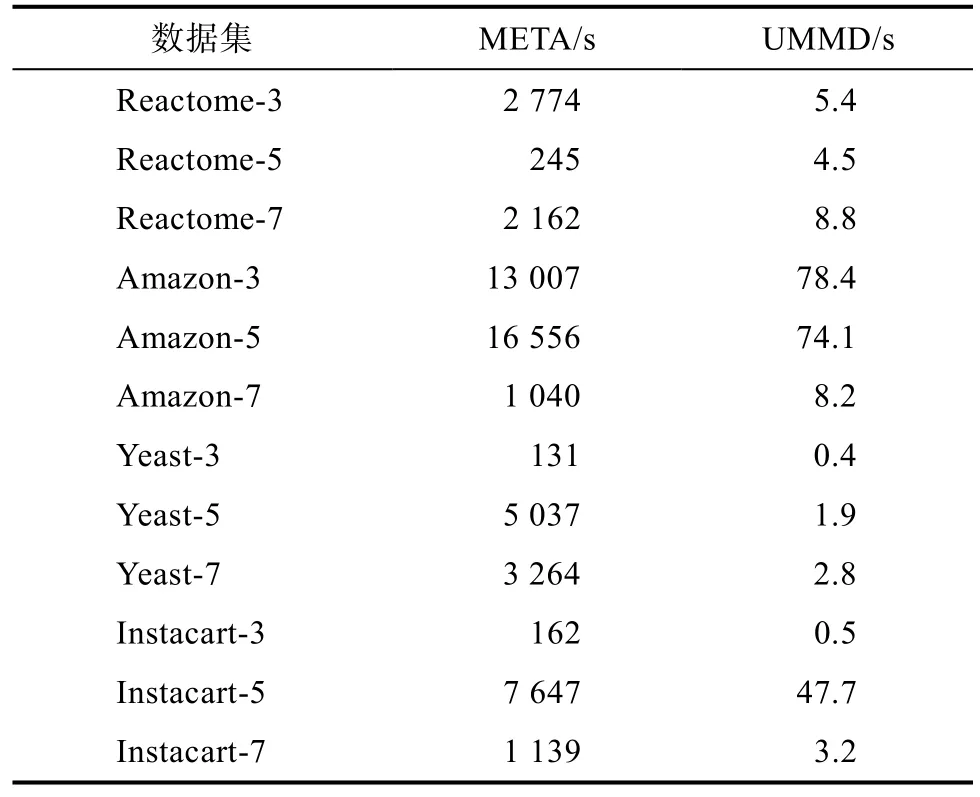
表4 删除100条边的更新时间Tab.4 the update time of deleting 100 edges
各算法在图上插入1 000条边的更新时间如表5所示。META算法在 Amazon-3、Amazon-4等多组数据集上无法在 Inf时间内完成更新,但UMMD算法在这些数据集上的最长更新时间是Amazon-4的78.4 s。UMMD算法的更新效率在插入1 000次边的条件下,比META算法约快3个数量级。在Yeast-3上UMMD算法快1364倍,在Instacart-3上快569倍。

表5 插入1 000条边的更新时间Tab.5 the update time of inserting 1 000 edges
各算法在图上删除1 000条边的更新时间如表6所示。观察实验结果,UMMD算法的更新效率比META算法快3个数量级左右。UMMD算法比META算法在Instacart-7上快1 910倍,在Amazon-7上快944倍。

表6 删除1 000条边的更新时间Tab.6 The update time of deleting 1000 edges
UMMD算法设计了合理有效的加边、减边策略,缩小了更新范围,避免了枚举操作。相比之下,META算法的更新方案,即重新枚举极大motif团,冗余度较高,效率较低。因为枚举是一个时间复杂度很高的操作,重新枚举又存在大量冗余,随着图更新次数的增加,META算法更新极大 motif团的时间开销会大幅增长。例如,在加减1 000次边时,META算法要进行相应次数的重新枚举。但UMMD算法基于现有的极大motif团进行更新操作,算法延展性良好。图更新次数变多时,UMMD算法的更新时间增加得较平缓。
4 结论
针对实际应用中异构信息网络动态变化,且现有极大 motif团挖掘算法不支持高效更新的问题,本文研究面向动态异构信息网络的极大motif团挖掘算法。本文提出了新的加边策略、减边策略,并设计了相应的算法。实验结果表明,在12个异构信息网络数据集上,UMMD算法的更新效率比基础算法META更加高效。例如,对图增删边时,在 Amazon、Reactome、Yeast、Instacart等数据集上,UMMD算法比META算法约快2-3个数量级。
