基于数字反向传输方法降低光纤通信系统复杂度的研究

李亚杰，葛 宇，张连连，方 彬，胡一龙

（河北建筑工程学院 电气工程学院，河北 张家口 075000）

0 引 言

随着无线互联网和智慧城域网的发展，传统的基于强度调制/直接检测（IM/DD）光纤通信系统不再满足高速数据传输的需求，如何提高系统的传输速率和容量，是光纤通信发展目前面临的重要问题。基于新型码型调制技术具有的信息加载方式灵活多变的特征，可有效提高通信系统的频谱利用率，增大系统的传输容量[1⁃2]。目前，广泛应用载波相位估计和反向传输补偿方案，特别是反向传输补偿方案，不仅可补偿光纤信道中的色散损伤，还可补偿非线性损伤，将其通过DSP 进行快速运算处理，能够大大提升通信系统的实时性，在降低线性和非线性损耗的同时，无需额外增加硬件成本。根据链路中色散管理方式的不同，将其分为两类：非色散管理（Non⁃dispersion Managed，NDM）和色散管理（Dispersion Managed，DM）。

本文基于非线性Schrödinger 方程推导出数字反向传输的理论模型，针对NDM 链路和DM 链路，探讨了步长、步数及发射功率等因素对系统误码率的影响，考察了数字反向传输方法补偿系统的色散和非线性损耗。以10×111 Gb/s POLMUX⁃RZ⁃DQPSK 信道组成的 WDM链路为例，分析了色散补偿、误码率及计算复杂度等性能，对比其数值仿真和实验结果，证明了DBP 方法在降低光纤通信系统复杂度方面的可行性。

1 数字反向传播理论

根据非线性 Schrödinger 方程（Nonlinear Schrödinger Equation，NLSE）[3]，得光信号传播近似模型为：

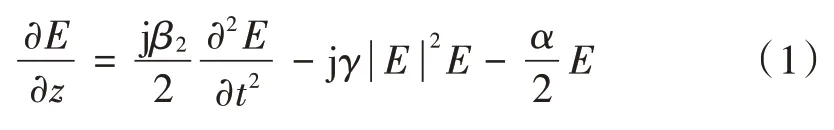
式中：E为光信号；z为传播方向；α为衰减系数；β2为色散参数；γ为非线性系数。

为了提高光信号的频谱利用率，采用偏振复用技术，需考虑两个正交偏振分量之间的线性相关和非线性相关。因此，式（1）可改写为：

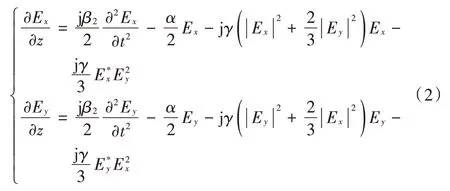
式中：Ex和Ey为两个正交偏振分量；“*”表示复共轭。

同理，式（2）可分解为线性和非线性两部分，即：

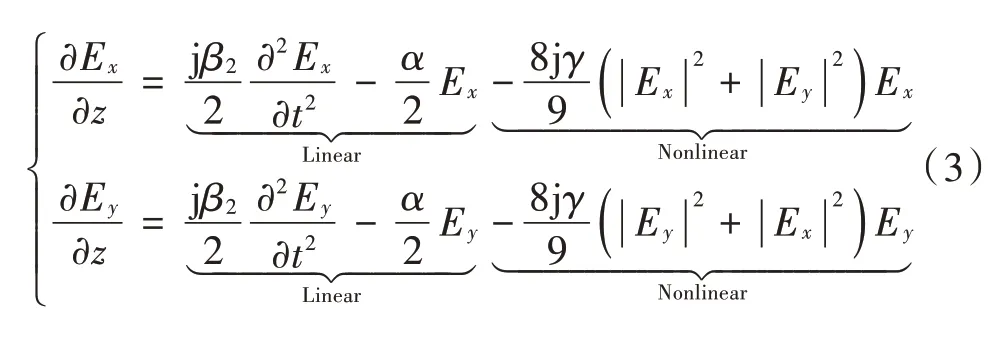
经化简，传播方程可表达为线性和非线性算符，即：

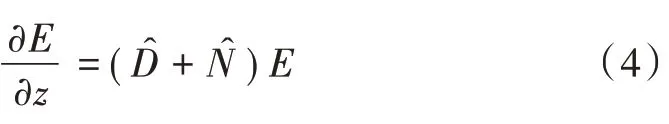
式中：为线性分量为非线性分量

求解可得，光信号的表达式为：

式中：z为光信号的传播位置；t为某一时刻；h为步长。

若步长h足够小时，式（5）可等效为分步傅里叶法（Split Step Fourier Method，SSFM），即：

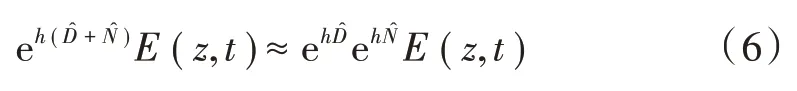
对于DBP 的性能而言，步长h的最优值始终等于零。在实际应用中这是不可能实现的，当步长h取到最优值时，SSFM 的步数将接近于无穷大，可得近似解为：

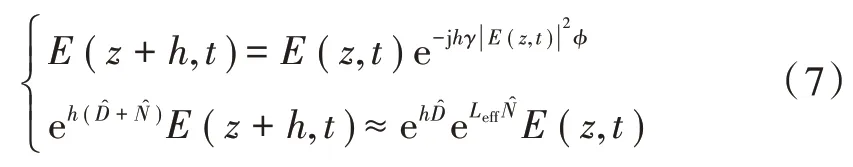
式中：ϕ∈[0,1]，是为了调整和优化非线性所引入的变量；Leff≤hϕ被定义为光纤长度[4]。

以 Wiener、Hammerstein 和 Wiener⁃Hammerstein三种不同的非线性光纤模型为例，求解结果如图1所示。

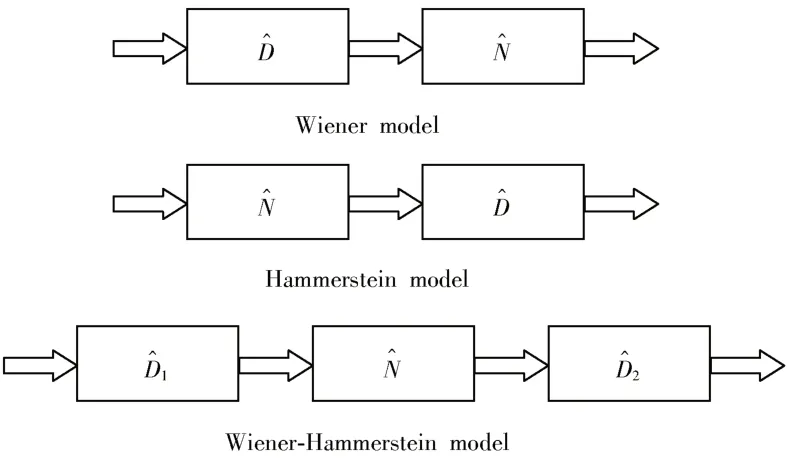
图1 三种不同的非线性光纤模型的SSFM 求解结果

在Wiener 模型中，线性部分位于非线性部分之前，而在Hammerstein 模型中则正好相反。然而，Wiener⁃Hammerstein 模型则是由三部分组成。本文中仅考虑Wiener⁃Hammerstein 模型。在不考虑光信号在光纤传输中的噪声影响，传输信号可用NLSE 的逆处理，即：

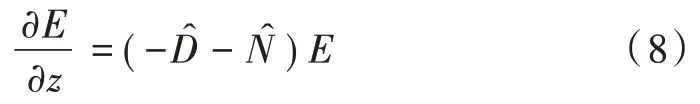
基于DBP 建立的补偿数学模型可以完全无失真地恢复出原信号，却无法直接求解该高阶非线性微分方程，但可利用数值分析方法进行求解。

2 光通信系统的DBP 方案

DBP 方法的性能评估可用最佳发射功率的增加量来衡量。将图1 中的Wiener⁃Hammerstein 模型应用于NDM 链路[5]，其性能可等效为DBP 方法中执行了一个Wiener 模型和两个级联步数的线性部分。当发射功率分别为 1 dBm、2 dBm、3 dBm、4 dBm、5 dBm 和 6 dBm时，利用 DBP 方法优化 Wiener⁃Hammerstein 模型中第一色散线性部分的长度，其系统误码率（lg（BER））与不同发射功率之间的关系如图2 所示。

由图2 可得：误码率并不是随着步数增加而单调增加，平均下来，第一色散线性部分存在最佳平均长度85%左右，这意味着通过优化第一色散线性部分的长度即可实现传输系统性能的提升。采用DBP 方法，大步数可有效消减非线性损伤，增大了数字处理计算的复杂度。因此，在不降低整体性能的前提下，可以考虑选取步数的临界值。对于由8 个步数综述所组成的NDM 链路，当对由2 个、4 个和8 个步数所组成的子集进行DBP时，系统误码率与发射功率之间的关系如图3 所示。

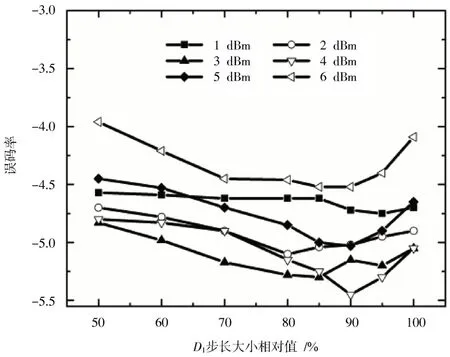
图2 传输系统的误码率与第一线性部分步长之间的变化关系

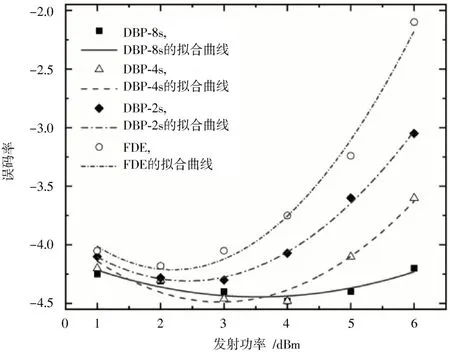
图3 传输系统的误码率与发射功率之间的变化关系

由图3 结果可知：发射功率相对较低（≤3 dBm）时，系统误码率并不受子集中步数个数的影响，结合未采用DBP 方法的发射功率变化曲线（FDE），可知发射功率的增加量为2 dB。由8 个步数所组成的NDM 链路，采用步数为4 的DBP 方法即可实现对传输系统性能的提升。

3 基于DBP 方法降低DM 链路的复杂度

DBP 方法进行色散补偿是通过在SSFM 中的线性部分和非线性部分之间相互作用实现的，进而保证DBP方法的准确性。对DM 链路而言，利用色散补偿光纤（Dispersion Compensating Fiber，DCF）进行在线色散补偿，残余色散则需特定的系统设计来完成补偿。若DM链路的色散被完全补偿，如图4 所示，其中每个步数的累积色散为0 ps/nm。

由图4 可得：利用SSFM 计算，DM 链路中所有步数的色散轮廓是完全相等的，这是由于步数开始和结束处的色散量相同。一个共15 个步数的完全色散补偿的DM 链路，当 DBP 步数分别采用 15 和 1 时，系统误码率与发射功率之间的关系如图5 所示。

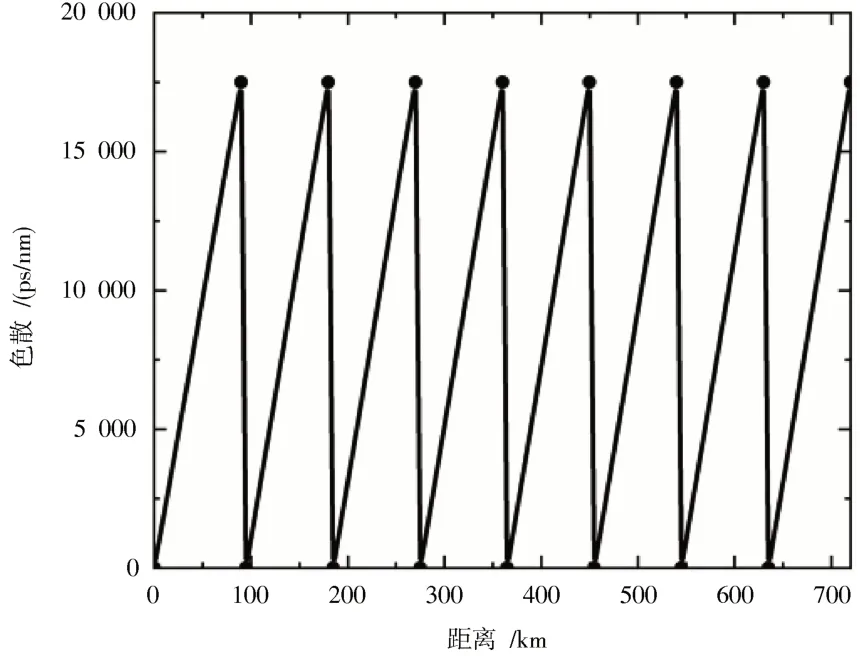
图4 完全色散补偿图

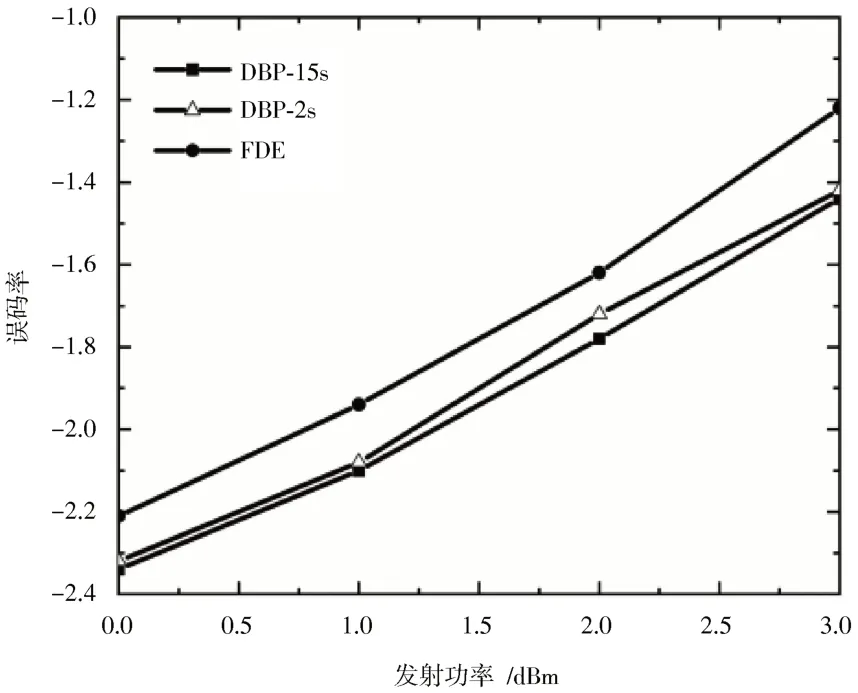
图5 完全色散补偿的DM 链路的误码率与发射功率之间的变化关系

结果表明：即使整个DM 链路只采用一步DBP 算法，相比于每个跨度上至少采用一步DBP 方法，其复杂度降低为95%，这也印证了前面得出的结论。

对于只补偿了90%的8×82 km DM链路而言，由7个步数组成，分别为4 个SSMF 和3 个DCF，对应的色散补偿如图6 所示。

从图6 中右侧A 点开始依次向左追迹水平线，可得DM 链路上具有相同累积色散的一系列点。显然，点A处的累积色散并不对应于下一步数开始处的值，而是对应于有效长度范围内的某一点。当步长为82 km 时，有效长度约等于25 km。可发现当第一线性部分的相对步长位于70%～100%之间时，利用W⁃H 模型的反向传输性能是最佳的。

综上所述，利用DBP 方法对光通信系统进行色散补偿的过程中，合理选择步长尤为重要，若所选取的步长较大，则会导致系统的非线性损伤补偿效果较差；若所选取的步长较小，则会导致计算量增加、运算速度较慢、影响系统的实时性，也会导致系统的非线性补偿效果较差。

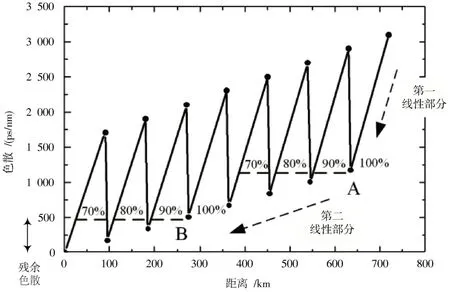
图6 欠10%色散补偿图

4 实验结果

采用由10×111 Gb/s POLMUX⁃RZ⁃DQPSK信道所组成的WDM 链路[6]，对后处理数据进行实验验证，其中总符号率为27.75 Gb/s，值为25 GSymbol/s，信道间隔为50 GHz。发射端输出信号预失真为-1 530 ps/nm，发射到由5×95 km SSMF所组成的循环回路中。每步数的在线色散补偿不足（Under⁃Compensation）是-85 ps/nm，对应于5%的欠补偿。前置色散补偿光纤和基于光纤的可调谐色散补偿用于将链路末端的净色散设置为接近于零。实验所得色散补偿图如图7所示，其传输距离为1 900 km。

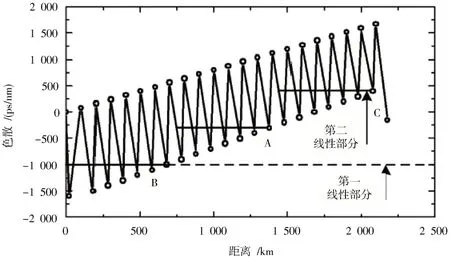
图7 WDM 链路的色散图

由实验结果可知：WDM 链路末端的残余色散约为300 ps/nm（点C），该值与A 中的色散所假设的值相差不大。因此，DBP 方法开始处的线性步骤可以省略不计，且当第二非线性步骤执行超过8 个步数时，最后一个线性补偿能使累积色散降低至85 ps/nm。该值对应于链路中最后一个步数开始处的色散值。在最后的6 个步数上非线性补偿已完全实现，剩余色散则由TDE 补偿。对于上述所考虑的WDM 链路，根据如图7 所示的色散图，确定所需的线性和非线性步数以及循环次数，其结果如表1 所示。

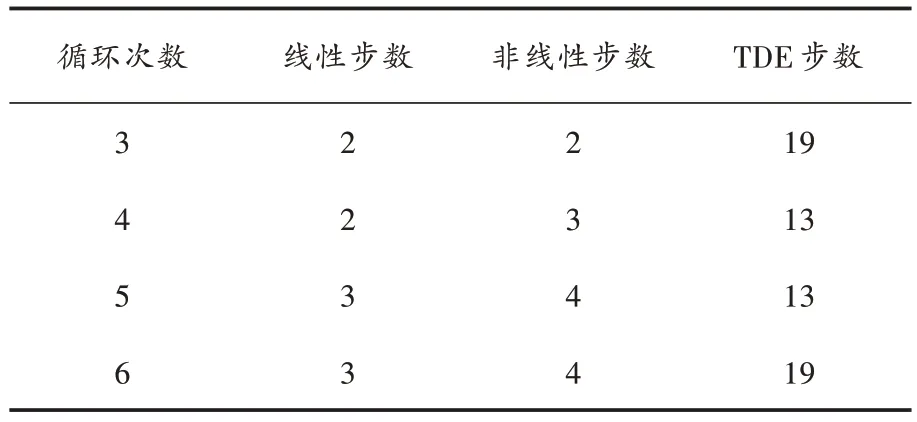
表1 WDM 链路中每个循环次数所包含的线性步数、非线性步数和TDE 步数

相对应地，分别利用FDE 方法、标准DBP 方法和第2 节中所提出的可降低复杂度的DBP 方法执行不同循环次数时，WDM 链路的误码率与循环次数之间的变化关系如图8 所示。

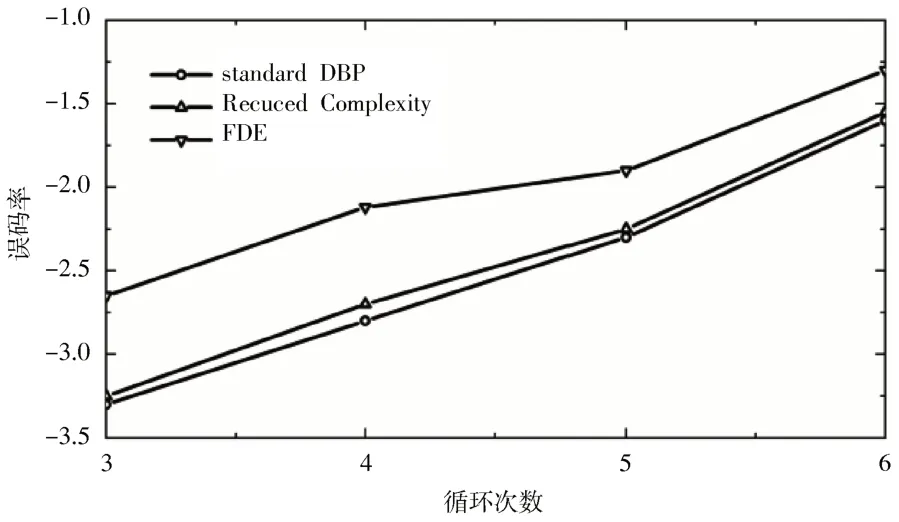
图8 三种方法计算的误码率与循环次数之间的变化关系

三种方法的误码率对比表明：DBP 方法可有效改进系统性能，可降低复杂度的DBP 方法性能与标准DBP 方法的性能相差并不大，该结果很好地验证了数值计算结果的正确性。为了衡量上述三种方法的性能，对上述结果进行复杂度的定量分析，结果如图9所示。

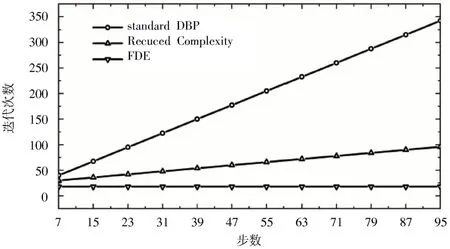
图9 三种方法计算所需迭代次数与步数之间的变化关系

图9 表明了所提出的可降低复杂度的DBP 方法相比于其他两种方法减少了计算量，相比于标准DBP 方法，本文方法可实现计算复杂度的显著降低。本实验很好地验证了DBP 算法的正确性及降低通信系统复杂度方面的有效性。

5 结 语

基于非线性Schrödinger 方程推导出了数字反向传输的理论模型。针对NDM 链路和DM 链路，在完全补偿和欠补偿的情况下，讨论了步长、步数及发射功率等因素对系统误码率的影响。最后，以10×111 Gb/s POLMUX⁃RZ⁃DQPSK 信道所组成的 WDM 链路为对象，利用FDE 方法、标准DBP 方法和文中的DBP 方法执行不同循环次数时，探讨了色散补偿、误码率及计算复杂度等性能，通过对比实验结果，充分证明了数字反向传输方法在降低光纤通信系统复杂度方面的可行性。