大规模MIMO⁃OFDM 结构化稀疏信道的重建方法
2021-03-08马惠艳何文旭
马惠艳,张 静,何文旭
(上海师范大学 信息与机电工程学院,上海 201400)
0 引 言
大规模MIMO 系统在基站端部署有数十根甚至数百根天线,利用空间复用和空间分集大幅度地提升无线通信系统的频谱利用率。基于频分双工(FDD)的系统与基于时分双工(TDD)的系统相比,具有低延迟和对称通信量等优势[1],在第五代移动通信系统中被广泛采用。研究表明,无线信道冲激响应(CIR)的大部分能量仅集中在较少的路径上,导致其在时域上呈现稀疏性。同时,在用户端单天线与基站端所有天线间的信道具有空间选择性,故呈现空间稀疏性的特点。与路径增益相比,路径延迟的变化要慢得多,使这种空间稀疏性在相干时间内几乎不变[2]。由于信道在时间延迟域和空间域中表现出稀疏性,可应用压缩感知理论获取信道状态信息(CSI)[3]。
目前已有较多稀疏信道估计算法是基于压缩感知(Compressive Sensing)理论的[4]。文献[5]在大规模MIMO⁃OFDM 系统中采用导频和发送端信道状态信息(CSI)反馈比特自适应的闭环框架,可使发送端在未知和时变的信道稀疏等级下用较少的导频和反馈开销成功地恢复CSI[5]。在此基础上,文献[6]通过给每根发射天线分配相同的导频子载波而非正交导频,当导频在时域上足够稀疏则可通过最小化傅里叶子矩阵的相关性,在接收端重构信道并获得良好的误码率性能。文献[7]利用信道散射路径的块稀疏性,使用角度域表示方法,并采用两级加权块ℓ1范数最小化准则估计出信道参数。文献[8]研究了时间相关性所形成的结构化稀疏性,采用压缩采样匹配追踪(CoSaMP)算法设计联合的信道训练和反馈方案来同时减小下行的训练导频和上行的反馈开销。为了增强稀疏恢复算法的鲁棒性,文献[9]通过信道支撑集的相关特性从已估计的信道矩阵中提取部分信道支撑集信息,采用辅助突发的最小绝对收缩与选择(LASSO)算法缓解信道恢复时对稀疏度的严格要求。文献[10]研究了多用户大规模MIMO 系统在用户信道矩阵中隐藏的联合稀疏结构,提出一种分布式压缩CSI 方案。大规模MIMO 采用非正交导频方案,利用MIMO 信道的空时公共稀疏性,文献[11]给出了一种用户自适应结构化子空间跟踪算法。为进一步优化系统的性能,一种改进的稀疏度自适应匹配追踪(ISAMP)算法在文献[12]中也获得了研究。
本文利用无线信道的时间相关性和空间相关性,结合Dice系数匹配准则以及变步长的方式,研究了稀疏度自适应的大规模MIMO⁃OFDM 信道估计算法,提出了一种基于Dice 系数的变步长稀疏度自适应信道估计算法。
1 系统模型
1.1 时延域空时相关特性
一个大规模MIMO 下行链路传输系统如图1 所示,包括一个配备有M根天线的基站。基站为小区内K个单天线用户服务。假设基站与用户间的信道为瑞利信道且包含L条相互独立的路径。

图1 大规模MIMO 系统模型
系统采用正交频分复用(OFDM)技术进行数据传输,设OFDM 的子载波总数为N,其中的导频子载波数为NP。将下行链路中第m根发射天线与一个用户天线之间的信道冲激响应(CIR)表示为:

式中:hm,r[l]为第l条路径的路径增益;r是时域中OFDM符号的索引;L为最大信道时延。
因为路径延迟比路径增益慢得多,时域CIR 中非零元素的位置变化很慢,可近似为常数。故相邻R个OFDM 信号表现出时间相关特性,如图2 所示,支撑集表示为:
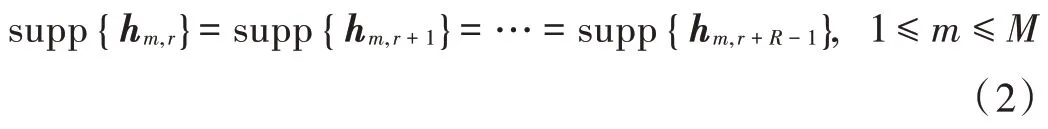
式中:supp{hm,r}={l:|hm,r[l]>ρth,1 ≤l≤L};ρth为噪声的最小值。

图2 大规模MIMO 信道的空时相关性
设基站端与用户端之间存在着公共散射体,不同发送接收天线对之间CIR 的稀疏特性绝大部分重叠。因此,M根发射与接收天线间的信道表现出空间相关性[10],支撑集表示为:

1.2 大规模MIMO⁃OFDM 系统的下行信道模型
考虑一个大规模MIMO⁃OFDM 系统,将用户端的接收信号表示为:

式中:Am为第m根天线发射的信号;F表示N×N维 DFT矩阵。经过去除保护间隔和DFT 变换后,提取出第r个OFDM 符号中的导频信号yr,yr表示为:

式中:ξ为一个OFDM 符号中分配给导频子载波的位置索引集合;Xm=diag{xm}是由xm构成的对角矩阵,xm为第m根天线发送的导频序列集合;FL是由F的前L行组成的子矩阵;vr是第r个OFDM 符号的加性高斯白噪声向量。式(5)可以简化为:

式中:Φ=[Φ1,Φ2,…,Φ M]表示一个NP×ML维矩阵;表示为ML× 1 维的等效信道冲激响应。
由于为高维稀疏信号,可利用压缩感知的理论将从低维信号yr重构出来。由大规模 MIMO 的空时相关稀疏性可知,不同的发射接收天线对的支撑集可以是相同的。
令dl,r=[h1,r(l),h2,r(l),…,hM,r(l)]T, 1 ≤l≤L,对进行重排列,信道冲激响应可等效为:

则˜可被看作L个块向量,每个块向量均为M×1维,且这M个元素同时为零或者非零元素,即˜ 为块稀疏信号。
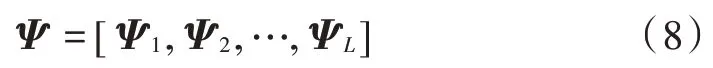
Ψ也由L个块稀疏矩阵构成,由此式(6)可表示为:

再结合上述所提到相邻的R个OFDM 信号表现出时间相关特性,式(9)可以等效为:

式 中 :观 测 矩 阵Y=[yr,yr+1,…,yr+R-1];D=为 等 效 信 道 增 益 矩 阵 ;V=[vr,vr+1,…,vr+R-1]为噪声矩阵。将信道增益矩阵D看作L×1 的块矩阵,每个块矩阵都按顺序取前M行得到子矩阵为:

式中:Dl为M×R的矩阵,第m行第r列元素表示基站第m根天线发送第r个OFDM 符号时第l条路径时延的信道增益值。
在获取CSI 时,表现出结构化稀疏性的等效冲激响应D为空时联合稀疏信号,即非零元素所在的位置均相同。因此,利用结构化压缩感知恢复算法将会得到更好的信道估计性能。
2 导频分配方案
传统的正交导频分配方案是基站端每根天线发送的导频符号占据不同的子载波,但这种方案的导频开销正比于基站的天线数。当天线数较多时,会造成较大的导频开销。本文采用文献[11]提出的非正交导频分配方案,系统在下行传输时,基站端不同天线发送的导频符号占用完全相同的子载波,可以使信道估计过程中的导频开销大大降低。
导频符号索引向量表示为:P=[P1,P2,…,PNP],(1 ≤P1<P2<…<PNP≤N)。导频分配方案如图3所示。
图3a)为正交导频示意图,这种方案通过插入空导频避免不同天线间的干扰,所产生的导频开销为MNP,导频开销较大;而图3b)的非正交导频方案则利用相同的子载波发送导频,导频开销只有NP。

图3 正交导频和非正交导频示意图
3 结构化稀疏度自适应改进算法
3.1 Dice 系数匹配准则
压缩感知重构算法常用内积法度量相似度,内积准则法为:

式中Z表示信号的残差Rt-1和测量矩阵中原子的相似度。
内积法的核心思想是计算测量矩阵中原子和残差信号矢量之间角度的余弦值。残差与测量矩阵原子的内积的绝对值越大,表明两个向量之间的相似度越高。因此式(12)可以用余弦法表示为:
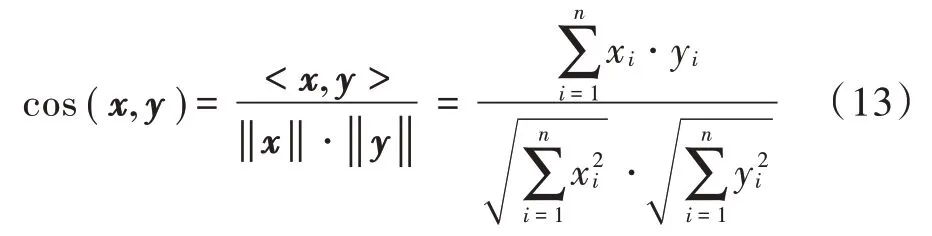
式中x,y均为任意向量。
由式(13)可知,余弦法的分母是由两个向量的几何平均值组成的。匹配原子时,会造成原始信号的部分重要成分丢失,导致原子匹配不准确或者算法重构时间较长。而Dice 系数匹配准则会利用其重要分量快速定位残差信号的主要成分,Dice 系数匹配准则可表示为:

由式(14)可以看出,Dice 系数是对两个向量的平方和求取算术平均值,从而能够更好地突出残差信号的重要成分,匹配出最佳原子集。由此可利用Dice 系数提高信道估计的计算效率。
3.2 基于Dice系数的变步长稀疏度自适应(DVSSP)算法
稀疏度自适应匹配追踪(SAMP)算法是一种基于未知稀疏度的贪婪迭代算法。该算法可以在信号稀疏度未知的情况下,以较高的概率重构原始信号,通过固定步长S逐步增大扩展支撑集来逼近信道的真实稀疏度,但SAMP 算法存在一定的缺陷,首先SAMP 算法是使用内积准则匹配原子,可能造成部分重要信息的丢失。其次,随着迭代次数的增加,步长也逐渐变大,因此匹配出的原子会过多,进而导致相似的原子被错误地选择,降低信号重构的准确性。最后,初始步长的选择也有很大争议,若初始步长过大,则无法准确地逼近信道稀疏度;若初始步长过小,会导致算法效率降低,因此,步长初始值的选取也会影响信号重构的效率与精度。
本文使用了一种基于Dice 系数的变步长稀疏度自适应算法,优化支撑集原子的选择,并由此减少匹配过程相似原子被再次选择。在未知稀疏度情况下,按阶段选择不同的方法更新支撑集长度,在算法起始阶段,初始估计的稀疏度会远小于信道的真实稀疏度,即如果满足条件且满足条件时,表示此次迭代获得的残差值大于前一次迭代的残差值,选取S=S×stage 的步长增长方式,以提高算法效率。当估计的稀疏度接近真实稀疏度时,即如果不满足条件但满足条件时,步长增长方式变更为其中为向上取整符号,迭代停止条件为其中ε1≫ε2,ε2代表信噪比的噪声能量值。通过指数增长的方法减小步长增量,实现对信号实际稀疏度K的逼近。算法步骤如下:
输入:测量矩阵Ψ,观测矩阵Y,初始稀疏度K;
输出:信号估计值{ }hm,q,其中,m=1,2,…,M,q=1,2,…,R+r-1


该方法可根据信道的实时状态,通过指数变步长的方式动态逼近信道的真实稀疏度,克服了实际环境中信道稀疏度未知的问题以及初始步长值的选择问题,也利于Dice 系数更好地突出信号的重要成分,提升了信道估计的性能。
4 仿真结果分析
设一个大规模MIMO⁃OFDM 系统的发射天线数目为32,接收天线数目为16。系统载波中心频率为2 GHz,信号带宽为 10 MHz,OFDM 符号有 4 096 个子载波,多普勒频移为80 Hz,信道模型采用ITU⁃VA 信道模型,并且各子信道服从瑞利分布。假定信道是时延域稀疏且稀疏度为K=6。在此场景和参数下,将OMP 算法、CoSaMP 算法以及SAMP 算法、最优最小二乘(oracle LS)以及本文给出的DVSSP 算法的性能进行对比。采用归一化均方误差(MSE)衡量信道恢复性能的优劣,假设信道估计的 CIR 为,将 MSE 定义为:

图 4 是 OMP 算法、CoSaMP 算法、SAMP 算法、Oracle LS 算法以及本文DVSSP 算法的MSE 性能对比。从图4可以看出,随着信噪比的增加,与SAMP 算法相比,本文给出的DVSSP 算法提升了信道估计的MSE 性能。本文算法通过Dice 系数的方法进行平方和求取算术平均值突出了信号的重要成分,并且在估计稀疏度接近真实稀疏度时,以指数方式减小步长的增长值,使得DVSSP 算法性能更加接近Oracle LS 算法。
图5 对比了信噪比为10 dB 时,在使用不同导频数情况下各算法的MSE 性能。从图5 可以看出,随着导频数的不断增加,5 种算法的估计MSE 均逐渐递减,并且本文提出的DVSSP 算法优于基于传统内积相似度计算的信道估计算法性能。在仿真的5 种算法中,DVSSP 算法的MSE性能在各导频数目下都最接近Oracle LS算法。

图4 不同SNR 下各算法MSE 性能对比
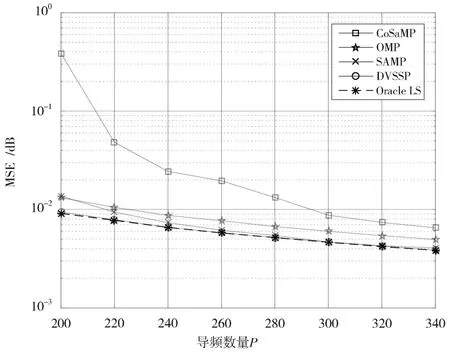
图5 不同导频数量下各算法MSE 性能对比
5 结 语
本文研究了大规模MIMO⁃OFDM 系统的空时相关性,利用结构化压缩感知理论中稀疏度自适应方法,提出了基于Dice 系数的变步长结构化稀疏信道的参数重建算法。与传统的将信道稀疏度作为先验条件的算法相比,本文算法可自适应地估计结构化稀疏信道的稀疏度并得到与最优LS 估计接近的估计性能,在实际应用中较易实现。
